Processo de contato (matemática) - Contact process (mathematics)

O processo de contato (em uma rede 1-D): Os sites ativos são indicados por círculos cinza e os sites inativos por círculos pontilhados. Os sites ativos podem ativar os sites inativos para qualquer lado deles a uma taxa r / 2 ou tornar-se inativos a uma taxa 1.

O processo de contato é um processo estocástico usado para modelar o crescimento populacional no conjunto de locais de um gráfico no qual os locais ocupados ficam vagos a uma taxa constante, enquanto os locais vagos são ocupados a uma taxa proporcional ao número de locais vizinhos ocupados. Portanto, se denotarmos pela constante de proporcionalidade, cada local permanece ocupado por um período de tempo aleatório que é exponencialmente distribuído pelo parâmetro 1 e coloca descendentes em cada local vizinho vazio em momentos de eventos de um parâmetro do processo de Poisson durante este período. Todos os processos são independentes uns dos outros e do período aleatório de tempo que os sites permanecem ocupados. O processo de contato também pode ser interpretado como um modelo para a propagação de uma infecção, pensando nas partículas como uma bactéria que se espalha sobre indivíduos que estão posicionados nos locais de , locais ocupados correspondem a indivíduos infectados, enquanto vagos correspondem a indivíduos saudáveis. ${\ displaystyle S}$${\ displaystyle \ lambda}$${\ displaystyle \ lambda}$${\ displaystyle S}$

A principal quantidade de interesse é o número de partículas no processo, digamos , na primeira interpretação, que corresponde ao número de sítios infectados na segunda. Portanto, o processo sobrevive sempre que o número de partículas for positivo para todos os tempos, o que corresponde ao caso de sempre haver indivíduos infectados no segundo tempo. Para qualquer gráfico infinito existe um valor crítico positivo e finito de forma que se então a sobrevivência do processo a partir de um número finito de partículas ocorra com probabilidade positiva, enquanto se sua extinção for quase certa. Observe que por reductio ad absurdum e o teorema do macaco infinito , a sobrevivência do processo é equivalente a , as , enquanto a extinção é equivalente a , as , e, portanto, é natural perguntar sobre a taxa em que quando o processo sobrevive. ${\ displaystyle N_ {t}}$${\ displaystyle S}$${\ displaystyle \ lambda _ {c}}$${\ displaystyle \ lambda> \ lambda _ {c}}$${\ displaystyle \ lambda <\ lambda _ {c}}$${\ displaystyle N_ {t} \ to \ infty}$${\ displaystyle t \ to \ infty}$${\ displaystyle N_ {t} \ a 0}$${\ displaystyle t \ to \ infty}$${\ displaystyle N_ {t} \ to \ infty}$

Definição Matemática

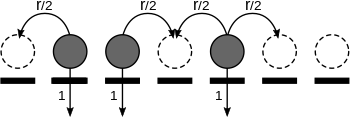
Se o estado do processo no momento for , então um local em está ocupado, digamos por uma partícula, se e vago se . O processo de contato é um processo de Markov de tempo contínuo com espaço de estado , onde é um gráfico finito ou contável , geralmente , e um caso especial de um sistema de partículas interagindo . Mais especificamente, a dinâmica do processo básico de contato é definida pelas seguintes taxas de transição: no local , ${\ displaystyle t}$${\ displaystyle \ xi _ {t}}$${\ displaystyle x}$${\ displaystyle S}$${\ displaystyle \ xi _ {t} (x) = 1}$${\ displaystyle \ xi _ {t} (x) = 0}$${\ displaystyle \ {0,1 \} ^ {S}}$${\ displaystyle S}$${\ displaystyle \ mathbb {Z} ^ {d}}$${\ displaystyle x}$

${\ displaystyle 1 \ rightarrow 0 \ quad {\ text {at rate}} 1,}$

${\ displaystyle 0 \ rightarrow 1 \ quad {\ text {na taxa}} \ lambda \ sum _ {y \,: \, y \, \ sim \, x} \ xi _ {t} (y),}$

onde a soma é sobre todos os vizinhos de em . Isso significa que cada site espera um tempo exponencial com a taxa correspondente e depois vira (então 0 se torna 1 e vice-versa). ${\ displaystyle y}$${\ displaystyle x}$${\ displaystyle S}$

Conexão com Percolação

O processo de contato é um processo estocástico que está intimamente ligado à teoria da percolação . Ted Harris (1974) observou que o processo de contato em ℤ ^d quando infecções e recuperações podem ocorrer apenas em tempos discretos corresponde à percolação de ligação uma etapa por vez no gráfico obtido orientando cada borda de ℤ ^{d + 1} em a direção do aumento do valor da coordenada. ${\ displaystyle \ {1,2, \ ldots, \}}$

A lei dos grandes números nos inteiros

Uma lei dos grandes números para o número de partículas no processo nos inteiros significa informalmente que, para todos os grandes , é aproximadamente igual a para alguma constante positiva . Ted Harris (1974) provou que, se o processo sobreviver, então a taxa de crescimento de é no máximo e pelo menos linear no tempo. Uma lei fraca dos grandes números (que o processo converge em probabilidade ) foi mostrada por Durrett (1980). Alguns anos depois, Durrett e Griffeath (1983) melhoraram isso para uma lei forte dos grandes números, dando convergência quase certa do processo. ${\ displaystyle t}$${\ displaystyle N_ {t}}$${\ displaystyle ct}$${\ displaystyle c = c (\ lambda)}$${\ displaystyle N_ {t}}$

Morra na criticidade

Para o processo de contato em todas as redes inteiras, um grande avanço veio em 1990, quando Bezuidenhout e Grimmett mostraram que o processo de contato também morre quase com certeza no valor crítico.

A conjectura de Durrett e o teorema do limite central

Durrett conjecturou em artigos de pesquisa e notas de palestras durante os anos 80 e início dos anos 90 a respeito do teorema do limite central para o processo de contato de Harris , viz. que, se o processo sobreviver, então para todos os grandes , igual e o erro igual multiplicado por um erro (aleatório) distribuído de acordo com uma distribuição gaussiana padrão . ${\ displaystyle t}$${\ displaystyle N_ {t}}$${\ displaystyle ct}$${\ displaystyle \ sigma {\ sqrt {t}}}$

A conjectura de Durrett acabou por ser correta para um valor diferente de como provado em 2018. ${\ displaystyle \ sigma}$

Referências

• C. Bezuidenhout e GR Grimmett , The critical contact process dies out , Ann. Probab. 18 (1990), 1462–1482.
• Durrett, Richard (1980). "Sobre o crescimento de processos de contato unidimensionais" . The Annals of Probability . 8 (5): 890–907. doi : 10.1214 / aop / 1176994619 .
• Durrett, Richard (1988). "Lecture Notes on Particle Systems and Percolation", Wadsworth.
• Durrett, Richard (1991). "O processo de contato, 1974-1989." Cornell University, Mathematical Sciences Institute.
• Durrett, Richard (1984). "Percolação Orientada em Número de Duas Dimensões" . The Annals of Probability . 12 (4): 999–1040. doi : 10.1214 / aop / 1176993140 .

• Durrett, Richard ; David Griffeath (1983). "Processos de contato supercríticos em Z" . The Annals of Probability . 11 (1): 1–15. doi : 10.1214 / aop / 1176993655 .
• Grimmett, Geoffrey (1999), Percolation , Springer

• Liggett, Thomas M. (1985). Interacting Particle Systems . Nova York: Springer Verlag. ISBN   978-0-387-96069-2 .
• Thomas M. Liggett , "Stochastic Interacting Systems: Contact, Voter and Exclusion Processes", Springer-Verlag, 1999.