Paradoxo de Cramer - Cramer's paradox
Na matemática , o paradoxo de Cramer ou o paradoxo de Cramer-Euler é a afirmação de que o número de pontos de intersecção de duas curvas de ordem superior no plano pode ser maior do que o número de pontos arbitrários que geralmente são necessários para definir uma dessas curvas. Recebeu o nome do matemático de Genebra, Gabriel Cramer .
Este paradoxo é o resultado de uma compreensão ingênua ou uma aplicação incorreta de dois teoremas:
- Teorema de Bézout (o número de pontos de intersecção de duas curvas algébricas é igual ao produto de seus graus, desde que certas condições necessárias sejam atendidas).
- Teorema de Cramer (uma curva de grau n é determinada por n ( n + 3) / 2 pontos, novamente assumindo que certas condições se mantêm).
Observe que para todo n ≥ 3, n 2 ≥ n ( n + 3) / 2, então, ingenuamente pareceria que para o grau três ou mais alto poderia haver pontos suficientes compartilhados por cada uma das duas curvas que esses pontos deveriam determinar qualquer um dos curvas com exclusividade.
A resolução do paradoxo é que, em certos casos degenerados, n ( n + 3) / 2 pontos não são suficientes para determinar uma curva com exclusividade.
História
O paradoxo foi publicado pela primeira vez por Colin Maclaurin . Cramer e Leonhard Euler se corresponderam sobre o paradoxo nas cartas de 1744 e 1745 e Euler explicou o problema a Cramer. Tornou-se conhecido como o paradoxo de Cramer após ser apresentado em seu livro de 1750, Introdução à l'analyse des lignes courbes algébriques , embora Cramer tenha citado Maclaurin como a fonte da declaração. Quase ao mesmo tempo, Euler publicou exemplos mostrando uma curva cúbica que não era exclusivamente definida por 9 pontos e discutiu o problema em seu livro Introductio in analysin infinitorum . O resultado foi divulgado por James Stirling e explicado por Julius Plücker .
Sem paradoxo para linhas e cônicas não degeneradas
Para curvas de primeira ordem (ou seja, linhas ), o paradoxo não ocorre, porque n = 1 então n 2 = 1 < n ( n + 3) / 2 = 2. Em geral, duas linhas distintas L 1 e L 2 se cruzam em um único ponto P , a menos que as linhas sejam de gradiente igual (inclinação), caso em que elas não se cruzam. Um único ponto não é suficiente para definir uma linha (dois são necessários); através do ponto P passam não apenas as duas linhas fornecidas, mas também um número infinito de outras linhas.
Da mesma forma, duas cônicas não degeneradas se cruzam em no máximo 4 pontos finitos no plano real, o que é menor que 3 2 = 9 dado como máximo pelo teorema de Bézout, e 5 pontos são necessários para definir uma cônica não degenerada.
O exemplo de Cramer para curvas cúbicas
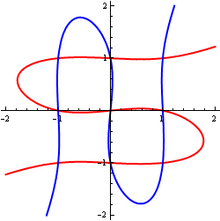
Em uma carta a Euler, Cramer apontou que as curvas cúbicas x 3 - x = 0 ey 3 - y = 0 se cruzam precisamente em 9 pontos (cada equação representa um conjunto de três linhas paralelas x = −1, x = 0, x = +1; ey = −1, y = 0, y = +1 respectivamente). Portanto, 9 pontos não são suficientes para determinar com exclusividade uma curva cúbica em casos degenerados como esses.
Resolução
Uma equação bivariada de grau n tem 1 + n ( n + 3) / 2 coeficientes, mas o conjunto de pontos descrito pela equação é preservado se a equação for dividida por um dos coeficientes, deixando um coeficiente igual a 1 e apenas n ( n + 3) / 2 coeficientes para caracterizar a curva. Dados n ( n + 3) / 2 pontos ( x i , y i ), cada um desses pontos pode ser usado para criar uma equação separada, substituindo-a na equação polinomial geral de grau n , dando n ( n + 3) / 2 equações lineares nos n ( n + 3) / 2 coeficientes desconhecidos. Se este sistema for não degenerado no sentido de ter um determinante diferente de zero , os coeficientes desconhecidos são determinados de forma única e, portanto, a equação polinomial e sua curva são determinadas de forma única. Mas se esse determinante for zero, o sistema é degenerado e os pontos podem estar em mais de uma curva de grau n .
Referências
links externos
- Ed Sandifer "Paradoxo de Cramer"
- Paradoxo de Cramer em MathPages