Matriz DFT - DFT matrix

Em matemática aplicada, uma matriz DFT é uma expressão de uma transformada discreta de Fourier (DFT) como uma matriz de transformação , que pode ser aplicada a um sinal por meio da multiplicação da matriz .

Definição

Uma DFT de N pontos é expressa como a multiplicação , onde é o sinal de entrada original, é a matriz DFT de N- por- N quadrada e é a DFT do sinal. ${\ displaystyle X = Wx}$${\ displaystyle x}$${\ displaystyle W}$ ${\ displaystyle X}$

A matriz de transformação pode ser definida como , ou equivalentemente: ${\ displaystyle W}$${\ displaystyle W = \ left ({\ frac {\ omega ^ {jk}} {\ sqrt {N}}} \ right) _ {j, k = 0, \ ldots, N-1}}$

${\ displaystyle W = {\ frac {1} {\ sqrt {N}}} {\ begin {bmatrix} 1 & 1 & 1 & 1 & \ cdots & 1 \\ 1 & \ omega & \ omega ^ {2} & \ omega ^ {3} & \ cdots & \ omega ^ {N-1} \\ 1 & \ omega ^ {2} & \ omega ^ {4} & \ omega ^ {6} & \ cdots & \ omega ^ {2 (N-1)} \\ 1 & \ omega ^ {3} & \ omega ^ {6} & \ omega ^ {9} & \ cdots & \ omega ^ {3 (N-1)} \\\ vdots & \ vdots & \ vdots & \ vdots & \ ddots & \ vdots \\ 1 & \ omega ^ {N-1} & \ omega ^ {2 (N-1)} & \ omega ^ {3 (N-1)} & \ cdots & \ omega ^ {(N -1) (N-1)} \ end {bmatrix}}}$,

onde é uma raiz N ésima primitiva da unidade em que . Podemos evitar escrever expoentes grandes por usar o fato de que para qualquer expoente temos a identidade. Esta é a matriz de Vandermonde para as raízes da unidade, até o fator de normalização. Observe que o fator de normalização na frente da soma ( ) e o sinal do expoente em ω são meramente convenções e diferem em alguns tratamentos. Toda a discussão a seguir se aplica independentemente da convenção, com no máximo pequenos ajustes. A única coisa importante é que as transformações para a frente e inversos têm expoentes de sinal oposto, e que o produto dos seus factores de normalização ser 1 / N . No entanto, a escolha aqui torna a matriz DFT resultante unitária , o que é conveniente em muitas circunstâncias. ${\ displaystyle \ omega = e ^ {- 2 \ pi i / N}}$${\ displaystyle i ^ {2} = - 1}$${\ displaystyle \ omega}$${\ displaystyle x}$${\ displaystyle \ omega ^ {x} = \ omega ^ {x \ mod N}.}$${\ displaystyle 1 / {\ sqrt {N}}}$${\ displaystyle 1 / {\ sqrt {N}}}$

Os algoritmos de transformada rápida de Fourier utilizam as simetrias da matriz para reduzir o tempo de multiplicação de um vetor por esta matriz, do usual . Técnicas semelhantes podem ser aplicadas para multiplicações por matrizes, como a matriz de Hadamard e a matriz de Walsh . ${\ displaystyle O (N ^ {2})}$

Exemplos

Dois pontos

O DFT de dois pontos é um caso simples, em que a primeira entrada é o DC (soma) e a segunda entrada é o AC (diferença).

${\ displaystyle W = {\ frac {1} {\ sqrt {2}}} {\ begin {bmatrix} 1 e 1 \\ 1 & -1 \ end {bmatrix}}}$

A primeira linha faz a soma e a segunda linha faz a diferença.

O fator de é tornar a transformação unitária (veja abaixo). ${\ displaystyle 1 / {\ sqrt {2}}}$

Quatro pontos

A matriz DFT de quatro pontos no sentido horário é a seguinte:

${\ displaystyle W = {\ frac {1} {\ sqrt {4}}} {\ begin {bmatrix} \ omega ^ {0} & \ omega ^ {0} & \ omega ^ {0} & \ omega ^ { 0} \\\ omega ^ {0} & \ omega ^ {1} & \ omega ^ {2} & \ omega ^ {3} \\\ omega ^ {0} & \ omega ^ {2} & \ omega ^ {4} & \ omega ^ {6} \\\ omega ^ {0} & \ omega ^ {3} & \ omega ^ {6} & \ omega ^ {9} \\\ end {bmatrix}} = {\ frac {1} {\ sqrt {4}}} {\ begin {bmatrix} 1 & 1 & 1 & 1 \\ 1 & -i & -1 & i \\ 1 & -1 & 1 & -1 \\ 1 & i & -1 & -i \ end {bmatrix}}}$

onde . ${\ displaystyle \ omega = e ^ {- {\ frac {2 \ pi i} {4}}} = - i}$

Oito pontos

A primeira potência inteira não trivial de dois casos é para oito pontos:

${\ displaystyle W = {\ frac {1} {\ sqrt {8}}} {\ begin {bmatrix} \ omega ^ {0} & \ omega ^ {0} & \ omega ^ {0} & \ omega ^ { 0} & \ omega ^ {0} & \ omega ^ {0} & \ omega ^ {0} & \ omega ^ {0} \\\ omega ^ {0} & \ omega ^ {1} & \ omega ^ { 2} & \ omega ^ {3} & \ omega ^ {4} & \ omega ^ {5} & \ omega ^ {6} & \ omega ^ {7} \\\ omega ^ {0} & \ omega ^ { 2} & \ omega ^ {4} & \ omega ^ {6} & \ omega ^ {8} & \ omega ^ {10} & \ omega ^ {12} & \ omega ^ {14} \\\ omega ^ { 0} & \ omega ^ {3} & \ omega ^ {6} & \ omega ^ {9} & \ omega ^ {12} & \ omega ^ {15} & \ omega ^ {18} & \ omega ^ {21 } \\\ omega ^ {0} & \ omega ^ {4} & \ omega ^ {8} & \ omega ^ {12} & \ omega ^ {16} & \ omega ^ {20} & \ omega ^ {24 } & \ omega ^ {28} \\\ omega ^ {0} & \ omega ^ {5} & \ omega ^ {10} & \ omega ^ {15} & \ omega ^ {20} & \ omega ^ {25 } & \ omega ^ {30} & \ omega ^ {35} \\\ omega ^ {0} & \ omega ^ {6} & \ omega ^ {12} & \ omega ^ {18} & \ omega ^ {24 } & \ omega ^ {30} & \ omega ^ {36} & \ omega ^ {42} \\\ omega ^ {0} & \ omega ^ {7} & \ omega ^ {14} & \ omega ^ {21 } & \ omega ^ {28} & \ omega ^ {35} & \ omega ^ {42} & \ omega ^ {49} \\\ end {bmatrix}} = {\ frac {1} {\ sqrt {8} }} {\ begin {bmatrix} 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & \ omega & -i & -i \ omega & -1 & - \ omega & i & i \ omega \\ 1 & -i & -1 & i & 1 & -i & -1 & i \\ 1 & -i \ omega & i & \ omega & -1 & i \ omega & -i & - \ omega \\ 1 & -1 & 1 & -1 & 1 & -1 & 1 & -1 \\ 1 & - \ omega & -i & i \ omega & -1 & \ omega & i & -i \ omega \\ 1 & i & -1 & -i & 1 & i & -1 & -i \\ 1 & i \ omega & i & - \ omega & -1 & -i \ omega & -i & \ omega \\\ end {bmatrix}}}$

Onde

${\ displaystyle \ omega = e ^ {- {\ frac {2 \ pi i} {8}}} = {\ frac {1} {\ sqrt {2}}} - {\ frac {i} {\ sqrt { 2}}}}$

(Observe isso .) ${\ displaystyle \ omega ^ {8 + n} = \ omega ^ {n}}$

A imagem a seguir mostra o DFT como uma multiplicação de matriz, com elementos da matriz representados por amostras de exponenciais complexas:

A parte real (onda cosseno) é denotada por uma linha sólida e a parte imaginária (onda senoidal) por uma linha tracejada.

A linha superior é composta por 1 (em escala para unitariedade), então ela "mede" o componente DC no sinal de entrada. A próxima linha é de oito amostras de um ciclo negativo de um exponencial complexo, ou seja, um sinal com uma frequência fracionária de -1/8, portanto, "mede" quanta "força" existe na frequência fracionária +1/8 no sinal. Lembre-se de que um filtro combinado compara o sinal com uma versão invertida no tempo de tudo o que estamos procurando, portanto, quando estamos procurando por fracfreq. 1/8 comparamos com fracfreq. -1/8 é por isso que esta linha é uma frequência negativa . A próxima linha é dois ciclos negativos de um exponencial complexo, amostrado em oito lugares, portanto, tem uma frequência fracionária de -1/4 e, portanto, "mede" a extensão em que o sinal tem uma frequência fracionária de +1/4. ${\ displaystyle 1 / {\ sqrt {8}}}$

O seguinte resume como funciona o DFT de 8 pontos, linha por linha, em termos de frequência fracionária:

• 0 mede quanto DC está no sinal
• -1/8 mede quanto do sinal tem uma frequência fracionária de +1/8
• -1/4 mede quanto do sinal tem uma frequência fracionária de +1/4
• -3/8 mede quanto do sinal tem uma frequência fracionária de +3/8
• -1/2 mede quanto do sinal tem uma frequência fracionária de +1/2
• −5/8 mede quanto do sinal tem uma frequência fracionária de +5/8
• -3/4 mede quanto do sinal tem uma frequência fracionária de +3/4
• −7/8 mede quanto do sinal tem uma frequência fracionária de +7/8

Equivalentemente, pode-se dizer que a última linha tem uma frequência fracionária de +1/8 e, portanto, medir quanto do sinal tem uma frequência fracionária de -1/8. Desta forma, pode-se dizer que as linhas superiores da matriz "medem" o conteúdo de freqüência positiva no sinal e as linhas inferiores medem o componente de freqüência negativa no sinal.

Transformada unitária

A DFT é (ou pode ser, por meio de seleção apropriada de escala) uma transformada unitária, ou seja, aquela que preserva energia. A escolha apropriada de escala para atingir a unidade é , de modo que a energia no domínio físico seja igual à energia no domínio de Fourier, ou seja, para satisfazer o teorema de Parseval . (Outras escalas, não unitárias, também são comumente usadas por conveniência computacional; por exemplo, o teorema da convolução assume uma forma ligeiramente mais simples com a escala mostrada no artigo da transformada discreta de Fourier .) ${\ displaystyle 1 / {\ sqrt {N}}}$

Outras propriedades

Para outras propriedades da matriz DFT, incluindo seus autovalores, conexão com convoluções, aplicações e assim por diante, consulte o artigo sobre transformada discreta de Fourier .

Um caso limite: o operador Fourier

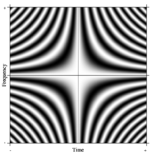
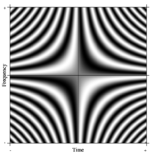
A noção de uma transformada de Fourier é prontamente generalizada . Uma generalização formal da DFT de N pontos pode ser imaginada considerando N arbitrariamente grande. No limite, o maquinário matemático rigoroso trata esses operadores lineares como as chamadas transformações integrais . Nesse caso, se fizermos uma matriz muito grande com exponenciais complexas nas linhas (ou seja, partes reais do cosseno e partes imaginárias do seno), e aumentarmos a resolução sem limite, nos aproximamos do kernel da equação integral de Fredholm de 2o tipo, ou seja, o operador de Fourier que define a transformada contínua de Fourier. Uma parte retangular desse operador Fourier contínuo pode ser exibida como uma imagem, análoga à matriz DFT, conforme mostrado à direita, onde o valor do pixel em escala de cinza denota a quantidade numérica.

Veja também

• Transformação multidimensional
• Matrizes de relógio e deslocamento

Referências

• The Transform and Data Compression Handbook de PC Yip, K. Ramamohan Rao - Veja o capítulo 2 para um tratamento do DFT baseado em grande parte na matriz DFT

links externos

• Operador de Fourier e decimação no tempo (DIT)