Filtro correspondente - Matched filter

No processamento de sinal , um filtro combinado é obtido correlacionando um sinal atrasado conhecido , ou modelo , com um sinal desconhecido para detectar a presença do modelo no sinal desconhecido. Isso é equivalente a convolver o sinal desconhecido com uma versão invertida no tempo conjugada do modelo. O filtro combinado é o filtro linear ideal para maximizar a relação sinal-ruído (SNR) na presença de ruído estocástico aditivo .

Filtros combinados são comumente usados ​​em radar , no qual um sinal conhecido é enviado e o sinal refletido é examinado em busca de elementos comuns do sinal de saída. A compressão de pulso é um exemplo de filtragem combinada. É assim chamado porque a resposta ao impulso é compatível com os sinais de pulso de entrada. Filtros combinados bidimensionais são comumente usados ​​no processamento de imagens , por exemplo, para melhorar o SNR de observações de raios-X. A filtragem combinada é uma técnica de demodulação com filtros LTI (linear time invariant) para maximizar o SNR. Ele era originalmente conhecido como filtro Norte .

Derivação

Derivação via álgebra matricial

A seção a seguir deriva o filtro combinado para um sistema de tempo discreto . A derivação para um sistema de tempo contínuo é semelhante, com somas substituídas por integrais.

O filtro combinado é o filtro linear , que maximiza a relação sinal-ruído de saída . ${\ displaystyle h}$

${\ displaystyle \ y [n] = \ sum _ {k = - \ infty} ^ {\ infty} h [nk] x [k],}$

onde é a entrada como uma função da variável independente e é a saída filtrada. Embora na maioria das vezes expressemos os filtros como a resposta ao impulso de sistemas de convolução, como acima (consulte a teoria do sistema LTI ), é mais fácil pensar no filtro combinado no contexto do produto interno , que veremos em breve. ${\ displaystyle x [k]}$${\ displaystyle k}$${\ displaystyle y [n]}$

Podemos derivar o filtro linear que maximiza a relação sinal-ruído de saída invocando um argumento geométrico. A intuição por trás do filtro casado se baseia em correlacionar o sinal recebido (um vetor) com um filtro (outro vetor) que é paralelo ao sinal, maximizando o produto interno. Isso melhora o sinal. Quando consideramos o ruído estocástico aditivo, temos o desafio adicional de minimizar a saída devido ao ruído escolhendo um filtro ortogonal ao ruído.

Vamos definir formalmente o problema. Procuramos um filtro, de modo que maximizemos a relação sinal-ruído de saída, onde a saída é o produto interno do filtro e o sinal observado . ${\ displaystyle h}$${\ displaystyle x}$

Nosso sinal observado consiste no sinal desejável e ruído aditivo : ${\ displaystyle s}$${\ displaystyle v}$

${\ displaystyle \ x = s + v. \,}$

Vamos definir a matriz de covariância do ruído, lembrando que esta matriz possui simetria Hermitiana , propriedade que se tornará útil na derivação:

${\ displaystyle \ R_ {v} = E \ {vv ^ {\ mathrm {H}} \} \,}$

onde denota a transposição conjugada de e denota expectativa . Vamos chamar nossa saída de, o produto interno de nosso filtro e o sinal observado de forma que ${\ displaystyle v ^ {\ mathrm {H}}}$${\ displaystyle v}$${\ displaystyle E}$${\ displaystyle y}$

${\ displaystyle \ y = \ sum _ {k = - \ infty} ^ {\ infty} h ^ {*} [k] x [k] = h ^ {\ mathrm {H}} x = h ^ {\ mathrm {H}} s + h ^ {\ mathrm {H}} v = y_ {s} + y_ {v}.}$

Agora definimos a relação sinal-ruído, que é nossa função objetivo, como a relação entre a potência da saída devido ao sinal desejado e a potência da saída devido ao ruído:

${\ displaystyle \ mathrm {SNR} = {\ frac {| y_ {s} | ^ {2}} {E \ {| y_ {v} | ^ {2} \}}}.}$

Reescrevemos o acima:

${\ displaystyle \ mathrm {SNR} = {\ frac {| h ^ {\ mathrm {H}} s | ^ {2}} {E \ {| h ^ {\ mathrm {H}} v | ^ {2} \}}}.}$

Queremos maximizar essa quantidade escolhendo . Expandindo o denominador de nossa função objetivo, temos ${\ displaystyle h}$

${\ displaystyle \ E \ {| h ^ {\ mathrm {H}} v | ^ {2} \} = E \ {(h ^ {\ mathrm {H}} v) {(h ^ {\ mathrm {H }} v)} ^ {\ mathrm {H}} \} = h ^ {\ mathrm {H}} E \ {vv ^ {\ mathrm {H}} \} h = h ^ {\ mathrm {H}} R_ {v} h. \,}$

Agora, nosso se torna ${\ displaystyle \ mathrm {SNR}}$

${\ displaystyle \ mathrm {SNR} = {\ frac {| h ^ {\ mathrm {H}} s | ^ {2}} {h ^ {\ mathrm {H}} R_ {v} h}}.}$

Vamos reescrever esta expressão com alguma manipulação de matriz. O motivo dessa medida aparentemente contraproducente ficará evidente em breve. Explorando a simetria Hermitiana da matriz de covariância , podemos escrever ${\ displaystyle R_ {v}}$

${\ displaystyle \ mathrm {SNR} = {\ frac {| {(R_ {v} ^ {1/2} h)} ^ {\ mathrm {H}} (R_ {v} ^ {- 1/2} s ) | ^ {2}} {{(R_ {v} ^ {1/2} h)} ^ {\ mathrm {H}} (R_ {v} ^ {1/2} h)}},}$

Gostaríamos de encontrar um limite superior para esta expressão. Para fazer isso, primeiro reconhecemos uma forma de desigualdade de Cauchy-Schwarz :

${\ displaystyle \ | a ^ {\ mathrm {H}} b | ^ {2} \ leq (a ^ {\ mathrm {H}} a) (b ^ {\ mathrm {H}} b), \,}$

o que quer dizer que o quadrado do produto interno de dois vetores só pode ser tão grande quanto o produto dos produtos internos individuais dos vetores. Esse conceito retorna à intuição por trás do filtro casado: esse limite superior é alcançado quando os dois vetores e são paralelos. Retomamos nossa derivação expressando o limite superior em nosso à luz da desigualdade geométrica acima: ${\ displaystyle a}$${\ displaystyle b}$${\ displaystyle \ mathrm {SNR}}$

${\ displaystyle \ mathrm {SNR} = {\ frac {| {(R_ {v} ^ {1/2} h)} ^ {\ mathrm {H}} (R_ {v} ^ {- 1/2} s ) | ^ {2}} {{(R_ {v} ^ {1/2} h)} ^ {\ mathrm {H}} (R_ {v} ^ {1/2} h)}} \ leq {\ frac {\ left [{(R_ {v} ^ {1/2} h)} ^ {\ mathrm {H}} (R_ {v} ^ {1/2} h) \ right] \ left [{(R_ {v} ^ {- 1/2} s)} ^ {\ mathrm {H}} (R_ {v} ^ {- 1/2} s) \ right]} {{(R_ {v} ^ {1 / 2} h)} ^ {\ mathrm {H}} (R_ {v} ^ {1/2} h)}}.}$

Nossa valente manipulação de matriz agora valeu a pena. Vemos que a expressão para nosso limite superior pode ser bastante simplificada:

${\ displaystyle \ mathrm {SNR} = {\ frac {| {(R_ {v} ^ {1/2} h)} ^ {\ mathrm {H}} (R_ {v} ^ {- 1/2} s ) | ^ {2}} {{(R_ {v} ^ {1/2} h)} ^ {\ mathrm {H}} (R_ {v} ^ {1/2} h)}} \ leq s ^ {\ mathrm {H}} R_ {v} ^ {- 1} s.}$

Podemos atingir esse limite superior se escolhermos,

${\ displaystyle \ R_ {v} ^ {1/2} h = \ alpha R_ {v} ^ {- 1/2} s}$

onde é um número real arbitrário. Para verificar isso, conectamos nossa expressão para a saída : ${\ displaystyle \ alpha}$${\ displaystyle \ mathrm {SNR}}$

${\ displaystyle \ mathrm {SNR} = {\ frac {| {(R_ {v} ^ {1/2} h)} ^ {\ mathrm {H}} (R_ {v} ^ {- 1/2} s ) | ^ {2}} {{(R_ {v} ^ {1/2} h)} ^ {\ mathrm {H}} (R_ {v} ^ {1/2} h)}} = {\ frac {\ alpha ^ {2} | {(R_ {v} ^ {- 1/2} s)} ^ {\ mathrm {H}} (R_ {v} ^ {- 1/2} s) | ^ {2 }} {\ alpha ^ {2} {(R_ {v} ^ {- 1/2} s)} ^ {\ mathrm {H}} (R_ {v} ^ {- 1/2} s)}} = {\ frac {| s ^ {\ mathrm {H}} R_ {v} ^ {- 1} s | ^ {2}} {s ^ {\ mathrm {H}} R_ {v} ^ {- 1} s }} = s ^ {\ mathrm {H}} R_ {v} ^ {- 1} s.}$

Assim, nosso filtro de correspondência ideal é

${\ displaystyle \ h = \ alpha R_ {v} ^ {- 1} s.}$

Freqüentemente, optamos por normalizar o valor esperado da potência da saída do filtro devido ao ruído para a unidade. Ou seja, nós restringimos

${\ displaystyle \ E \ {| y_ {v} | ^ {2} \} = 1. \,}$

Essa restrição implica um valor de , para o qual podemos resolver: ${\ displaystyle \ alpha}$

${\ displaystyle \ E \ {| y_ {v} | ^ {2} \} = \ alpha ^ {2} s ^ {\ mathrm {H}} R_ {v} ^ {- 1} s = 1,}$

produzindo

${\ displaystyle \ \ alpha = {\ frac {1} {\ sqrt {s ^ {\ mathrm {H}} R_ {v} ^ {- 1} s}}},}$

dando-nos nosso filtro normalizado,

${\ displaystyle \ h = {\ frac {1} {\ sqrt {s ^ {\ mathrm {H}} R_ {v} ^ {- 1} s}}} R_ {v} ^ {- 1} s.}$

Se quisermos escrever a resposta ao impulso do filtro para o sistema de convolução, é simplesmente a inversão de tempo conjugada complexa da entrada . ${\ displaystyle h}$${\ displaystyle s}$

Embora tenhamos derivado o filtro casado em tempo discreto, podemos estender o conceito para sistemas de tempo contínuo se substituirmos pela função de autocorrelação de tempo contínuo do ruído, assumindo um sinal contínuo , ruído contínuo e um filtro contínuo . ${\ displaystyle R_ {v}}$${\ displaystyle s (t)}$${\ displaystyle v (t)}$${\ displaystyle h (t)}$

Derivação via Lagrangiana

Alternativamente, podemos resolver para o filtro casado resolvendo nosso problema de maximização com um Lagrangiano. Novamente, o filtro combinado se esforça para maximizar a relação sinal-ruído de saída ( ) de um sinal determinístico filtrado em ruído aditivo estocástico. A sequência observada, novamente, é ${\ displaystyle \ mathrm {SNR}}$

${\ displaystyle \ x = s + v, \,}$

com a matriz de covariância de ruído,

${\ displaystyle \ R_ {v} = E \ {vv ^ {\ mathrm {H}} \}. \,}$

A relação sinal-ruído é

${\ displaystyle \ mathrm {SNR} = {\ frac {| y_ {s} | ^ {2}} {E \ {| y_ {v} | ^ {2} \}}},}$

onde e . ${\ displaystyle y_ {s} = h ^ {\ mathrm {H}} s}$${\ displaystyle y_ {v} = h ^ {\ mathrm {H}} v}$

Avaliando a expressão no numerador, temos

${\ displaystyle \ | y_ {s} | ^ {2} = {y_ {s}} ^ {\ mathrm {H}} y_ {s} = h ^ {\ mathrm {H}} ss ^ {\ mathrm {H }} h. \,}$

e no denominador,

${\ displaystyle \ E \ {| y_ {v} | ^ {2} \} = E \ {{y_ {v}} ^ {\ mathrm {H}} y_ {v} \} = E \ {h ^ { \ mathrm {H}} vv ^ {\ mathrm {H}} h \} = h ^ {\ mathrm {H}} R_ {v} h. \,}$

A relação sinal-ruído torna-se

${\ displaystyle \ mathrm {SNR} = {\ frac {h ^ {\ mathrm {H}} ss ^ {\ mathrm {H}} h} {h ^ {\ mathrm {H}} R_ {v} h}} .}$

Se agora restringirmos o denominador a 1, o problema de maximização é reduzido para maximizar o numerador. Podemos então formular o problema usando um multiplicador de Lagrange : ${\ displaystyle \ mathrm {SNR}}$

${\ displaystyle \ h ^ {\ mathrm {H}} R_ {v} h = 1}$

${\ displaystyle \ {\ mathcal {L}} = h ^ {\ mathrm {H}} ss ^ {\ mathrm {H}} h + \ lambda (1-h ^ {\ mathrm {H}} R_ {v} h )}$

${\ displaystyle \ \ nabla _ {h ^ {*}} {\ mathcal {L}} = ss ^ {\ mathrm {H}} h- \ lambda R_ {v} h = 0}$

${\ displaystyle \ (ss ^ {\ mathrm {H}}) h = \ lambda R_ {v} h}$

que reconhecemos como um problema de autovalor generalizado

${\ displaystyle \ h ^ {\ mathrm {H}} (ss ^ {\ mathrm {H}}) h = \ lambda h ^ {\ mathrm {H}} R_ {v} h.}$

Como é de classificação unitária, ele tem apenas um autovalor diferente de zero. Pode-se mostrar que este autovalor é igual a ${\ displaystyle ss ^ {\ mathrm {H}}}$

${\ displaystyle \ \ lambda _ {\ max} = s ^ {\ mathrm {H}} R_ {v} ^ {- 1} s,}$

produzindo o seguinte filtro de correspondência ideal

${\ displaystyle \ h = {\ frac {1} {\ sqrt {s ^ {\ mathrm {H}} R_ {v} ^ {- 1} s}}} R_ {v} ^ {- 1} s.}$

Este é o mesmo resultado encontrado na subseção anterior.

Interpretação como um estimador de mínimos quadrados

Derivação

A filtragem combinada também pode ser interpretada como um estimador de mínimos quadrados para a localização e escala ideais de um determinado modelo ou gabarito. Mais uma vez, deixe a sequência observada ser definida como

${\ displaystyle \ x_ {k} = s_ {k} + v_ {k}, \,}$

onde é ruído médio zero não correlacionado. O sinal é considerado uma versão escalonada e deslocada de uma sequência de modelo conhecida : ${\ displaystyle v_ {k}}$${\ displaystyle s_ {k}}$${\ displaystyle f_ {k}}$

${\ displaystyle \ s_ {k} = \ mu _ {0} \ cdot f_ {k-j_ {0}}}$

Queremos encontrar estimativas ideais e para o deslocamento e escala desconhecidos , minimizando os mínimos quadrados residuais entre a sequência observada e uma "sequência de sondagem" : ${\ displaystyle j ^ {*}}$${\ displaystyle \ mu ^ {*}}$${\ displaystyle j_ {0}}$${\ displaystyle \ mu _ {0}}$${\ displaystyle x_ {k}}$${\ displaystyle h_ {jk}}$

${\ displaystyle \ j ^ {*}, \ mu ^ {*} = \ arg \ min _ {j, \ mu} \ sum _ {k} \ left (x_ {k} - \ mu \ cdot h_ {jk} \ direita) ^ {2}}$

Mais tarde, o apropriado será o filtro correspondente, mas ainda não foi especificado. Expandindo e o quadrado dentro da soma produz ${\ displaystyle h_ {jk}}$${\ displaystyle x_ {k}}$

${\ displaystyle \ j ^ {*}, \ mu ^ {*} = \ arg \ min _ {j, \ mu} \ left [\ sum _ {k} (s_ {k} + v_ {k}) ^ { 2} + \ mu ^ {2} \ sum _ {k} h_ {jk} ^ {2} -2 \ mu \ sum _ {k} s_ {k} h_ {jk} -2 \ mu \ sum _ {k } v_ {k} h_ {jk} \ right]}$ .

O primeiro termo entre parênteses é uma constante (uma vez que o sinal observado é dado) e não tem influência na solução ótima. O último termo tem valor esperado constante porque o ruído não é correlacionado e tem média zero. Podemos, portanto, retirar ambos os termos da otimização. Depois de inverter o sinal, obtemos o problema de otimização equivalente

${\ displaystyle \ j ^ {*}, \ mu ^ {*} = \ arg \ max _ {j, \ mu} \ left [2 \ mu \ sum _ {k} s_ {k} h_ {jk} - \ mu ^ {2} \ sum _ {k} h_ {jk} ^ {2} \ right]}$ .

Definir a derivada wrt para zero fornece uma solução analítica para : ${\ displaystyle \ mu}$${\ displaystyle \ mu ^ {*}}$

${\ displaystyle \ \ mu ^ {*} = {\ frac {\ sum _ {k} s_ {k} h_ {jk}} {\ sum _ {k} h_ {jk} ^ {2}}}}$ .

Inserir isso em nossa função objetivo produz um problema de maximização reduzido para apenas : ${\ displaystyle j ^ {*}}$

${\ displaystyle \ j ^ {*} = \ arg \ max _ {j} {\ frac {\ left (\ sum _ {k} s_ {k} h_ {jk} \ right) ^ {2}} {\ sum _ {k} h_ {jk} ^ {2}}}}$ .

O numerador pode ter um limite superior por meio da desigualdade de Cauchy-Schwarz :

${\ displaystyle \ {\ frac {\ left (\ sum _ {k} s_ {k} h_ {jk} \ right) ^ {2}} {\ sum _ {k} h_ {jk} ^ {2}}} \ leq {\ frac {\ sum _ {k} s_ {k} ^ {2} \ cdot \ sum _ {k} h_ {jk} ^ {2}} {\ sum _ {k} h_ {jk} ^ { 2}}} = \ sum _ {k} s_ {k} ^ {2} = \ mathrm {const}}$ .

O problema de otimização assume seu máximo quando a igualdade é mantida nesta expressão. De acordo com as propriedades da desigualdade de Cauchy-Schwarz, isso só é possível quando

${\ displaystyle \ h_ {jk} = \ nu \ cdot s_ {k} = \ kappa \ cdot f_ {k-j_ {0}}}$ .

para constantes arbitrárias diferentes de zero ou , e a solução ótima é obtida como desejado. Assim, nossa "sequência de sondagem" deve ser proporcional ao modelo do sinal , e a escolha conveniente produz o filtro correspondente ${\ displaystyle \ nu}$${\ displaystyle \ kappa}$${\ displaystyle j ^ {*} = j_ {0}}$${\ displaystyle h_ {jk}}$${\ displaystyle f_ {k-j_ {0}}}$${\ displaystyle \ kappa = 1}$

${\ displaystyle \ h_ {k} = f _ {- k}}$ .

Observe que o filtro é o modelo de sinal espelhado. Isso garante que a operação a ser aplicada para encontrar o ótimo é de fato a convolução entre a sequência observada e o filtro casado . A sequência filtrada assume seu máximo na posição em que a sequência observada melhor corresponde (no sentido de mínimos quadrados) ao modelo de sinal . ${\ displaystyle \ sum _ {k} x_ {k} h_ {jk}}$${\ displaystyle x_ {k}}$${\ displaystyle h_ {k}}$${\ displaystyle x_ {k}}$${\ displaystyle f_ {k}}$

Implicações

O filtro combinado pode ser derivado de uma variedade de maneiras, mas como um caso especial de um procedimento de mínimos quadrados, ele também pode ser interpretado como um método de máxima verossimilhança no contexto de um modelo de ruído gaussiano (colorido) e a probabilidade de Whittle associada . Se o sinal transmitido não possuísse parâmetros desconhecidos (como tempo de chegada, amplitude, ...), então o filtro casado iria, de acordo com o lema de Neyman-Pearson , minimizar a probabilidade de erro. No entanto, uma vez que o sinal exato geralmente é determinado por parâmetros desconhecidos que são efetivamente estimados (ou ajustados ) no processo de filtragem, o filtro combinado constitui uma estatística de verossimilhança máxima generalizada (teste). A série temporal filtrada pode então ser interpretada como (proporcional) à probabilidade de perfil , a probabilidade condicional maximizada em função do parâmetro de tempo. Isso implica, em particular, que a probabilidade de erro (no sentido de Neyman e Pearson, ou seja, a respeito da maximização da probabilidade de detecção para uma dada probabilidade de alarme falso) não é necessariamente ótima. O que é comumente referido como a relação sinal-ruído (SNR) , que deve ser maximizada por um filtro casado, neste contexto corresponde a , onde é a razão de verossimilhança maximizada (condicionalmente). ${\ displaystyle {\ sqrt {2 \ log ({\ mathcal {L}})}}}$${\ displaystyle {\ mathcal {L}}}$

A construção do filtro combinado é baseada em um espectro de ruído conhecido . Na realidade, entretanto, o espectro de ruído é geralmente estimado a partir de dados e, portanto, conhecido apenas com uma precisão limitada. Para o caso de um espectro incerto, o filtro casado pode ser generalizado para um procedimento iterativo mais robusto com propriedades favoráveis ​​também em ruído não gaussiano.

Interpretação no domínio da frequência

Quando visto no domínio da frequência, é evidente que o filtro combinado aplica a maior ponderação aos componentes espectrais que exibem a maior razão sinal-ruído (ou seja, grande peso onde o ruído é relativamente baixo e vice-versa). Em geral, isso requer uma resposta de frequência não plana, mas a "distorção" associada não é motivo de preocupação em situações como radar e comunicações digitais , onde a forma de onda original é conhecida e o objetivo é a detecção deste sinal contra o ruído de fundo . Do lado técnico, o filtro combinado é um método de quadrados mínimos ponderados com base nos dados de domínio de frequência ( heterocedástico ) (onde os "pesos" são determinados por meio do espectro de ruído, consulte também a seção anterior), ou equivalentemente, um mínimo método dos quadrados aplicado aos dados branqueados .

Exemplos

Filtro compatível no radar e sonar

Filtros combinados são freqüentemente usados ​​na detecção de sinal . Por exemplo, suponha que desejamos julgar a distância de um objeto refletindo um sinal dele. Podemos escolher transmitir uma sinusóide de tom puro a 1 Hz. Assumimos que nosso sinal recebido é uma forma atenuada e com mudança de fase do sinal transmitido com ruído adicionado.

Para julgar a distância do objeto, correlacionamos o sinal recebido com um filtro casado, que, no caso de ruído branco (não correlacionado) , é outra senóide de tom puro de 1 Hz. Quando a saída do sistema de filtro combinado excede um certo limite, concluímos com alta probabilidade que o sinal recebido foi refletido do objeto. Usando a velocidade de propagação e o tempo em que observamos pela primeira vez o sinal refletido, podemos estimar a distância do objeto. Se mudarmos a forma do pulso de uma maneira especialmente projetada, a relação sinal-ruído e a resolução da distância podem ser ainda melhoradas após a filtragem combinada: esta é uma técnica conhecida como compressão de pulso .

Além disso, os filtros combinados podem ser usados ​​em problemas de estimativa de parâmetro (consulte a teoria de estimativa ). Para retornar ao nosso exemplo anterior, podemos desejar estimar a velocidade do objeto, além de sua posição. Para explorar o efeito Doppler , gostaríamos de estimar a frequência do sinal recebido. Para fazer isso, podemos correlacionar o sinal recebido com vários filtros combinados de sinusóides em frequências variáveis. O filtro casado com a saída mais alta revelará, com alta probabilidade, a frequência do sinal refletido e nos ajudará a determinar a velocidade do objeto. Este método é, na verdade, uma versão simples da transformada discreta de Fourier (DFT) . O DFT pega uma entrada complexa avaliada e correlaciona-a com filtros combinados, correspondendo a exponenciais complexas em frequências diferentes, para produzir números de valores complexos correspondentes às amplitudes e fases relativas dos componentes senoidais (consulte Indicação de alvo móvel ). ${\ displaystyle N}$${\ displaystyle N}$${\ displaystyle N}$${\ displaystyle N}$

Filtro compatível em comunicações digitais

O filtro combinado também é usado em comunicações. No contexto de um sistema de comunicação que envia mensagens binárias do transmissor para o receptor através de um canal com ruído, um filtro combinado pode ser usado para detectar os pulsos transmitidos no sinal recebido com ruído.

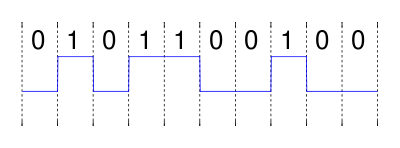
Imagine que queremos enviar a sequência "0101100100" codificada em Non-return-to-zero (NRZ) não polar através de um determinado canal.

Matematicamente, uma sequência no código NRZ pode ser descrita como uma sequência de pulsos de unidade ou funções retas deslocadas , cada pulso sendo ponderado por +1 se o bit for "1" e por -1 se o bit for "0". Formalmente, o fator de escala para o bit é, ${\ displaystyle k ^ {\ mathrm {th}}}$

${\ displaystyle \ a_ {k} = {\ begin {cases} +1, & {\ mbox {if bit}} k {\ mbox {is 1}}, \\ - 1, & {\ mbox {if bit} } k {\ mbox {é 0}}. \ end {casos}}}$

Podemos representar nossa mensagem, como a soma dos pulsos unitários deslocados: ${\ displaystyle M (t)}$

${\ displaystyle \ M (t) = \ sum _ {k = - \ infty} ^ {\ infty} a_ {k} \ times \ Pi \ left ({\ frac {t-kT} {T}} \ right) .}$

onde é a duração de um bit. ${\ displaystyle T}$

Assim, o sinal a ser enviado pelo transmissor é

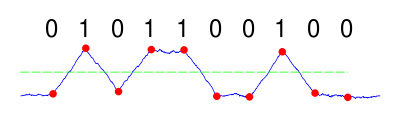
Se modelarmos nosso canal ruidoso como um canal AWGN , o ruído gaussiano branco é adicionado ao sinal. Na extremidade do receptor, para uma relação sinal-ruído de 3 dB, isso pode ser parecido com:

Um primeiro olhar não revelará a sequência original transmitida. Há uma alta potência de ruído em relação à potência do sinal desejado (ou seja, há uma baixa relação sinal-ruído ). Se o receptor tivesse que fazer uma amostragem desse sinal nos momentos corretos, a mensagem binária resultante possivelmente desmentiria a mensagem original transmitida.

Para aumentar nossa relação sinal-ruído, passamos o sinal recebido por um filtro casado. Neste caso, o filtro deve corresponder a um pulso NRZ (equivalente a um "1" codificado no código NRZ). Precisamente, a resposta de impulso do filtro compatível ideal, supondo que o ruído branco (não correlacionado) deve ser uma versão em escala conjugada de complexo invertida no tempo do sinal que estamos procurando. Nós escolhemos

${\ displaystyle \ h (t) = \ Pi \ left ({\ frac {t} {T}} \ right).}$

Neste caso, devido à simetria, o complexo conjugado invertido de é de fato , permitindo-nos chamar a resposta ao impulso de nosso sistema de convolução de filtro casado. ${\ displaystyle h (t)}$${\ displaystyle h (t)}$${\ displaystyle h (t)}$

Depois de convolver com o filtro correspondente correto, o sinal resultante, é, ${\ displaystyle M _ {\ mathrm {filtrado}} (t)}$

${\ displaystyle \ M _ {\ mathrm {filtrado}} (t) = M (t) * h (t)}$

onde denota convolução. ${\ displaystyle *}$

Que agora pode ser amostrado com segurança pelo receptor nos instantes de amostragem corretos e comparado a um limite apropriado, resultando em uma interpretação correta da mensagem binária.

Filtro compatível na astronomia de ondas gravitacionais

Filtros combinados desempenham um papel central na astronomia de ondas gravitacionais . A primeira observação de ondas gravitacionais foi baseada na filtragem em grande escala da saída de cada detector para sinais semelhantes à forma esperada, seguido por rastreio subsequente para disparos coincidentes e coerentes entre os dois instrumentos. As taxas de falsos alarmes e, com isso, a significância estatística da detecção foram avaliadas usando métodos de reamostragem . A inferência sobre os parâmetros da fonte astrofísica foi concluída usando métodos bayesianos baseados em modelos teóricos parametrizados para a forma de onda do sinal e (novamente) na probabilidade de Whittle .

Veja também

• Periodograma
• Retroprojeção filtrada (transformação de Radon)
• Filtro digital
• Processamento de sinal estatístico
• Probabilidade de Whittle
• Probabilidade de perfil
• Teoria de detecção
• Problema de múltiplas comparações
• Capacidade do canal
• Teorema de codificação de canal ruidoso
• Estimativa de densidade espectral
• Filtro de mínimos quadrados (LMS)
• Filtro Wiener
• Classificação Múltipla de Sinais (MUSIC), um método de superresolução paramétrica popular
• SAMV

Notas

Referências

Leitura adicional

• Turin, GL (1960). "Uma introdução aos filtros correspondentes" . Transações IRE na Teoria da Informação . 6 (3): 311–329. doi : 10.1109 / TIT.1960.1057571 .
• Wainstein, LA; Zubakov, VD (1962). Extração de sinais de ruído . Englewood Cliffs, NJ: Prentice-Hall .
• Melvin, WL (2004). "Uma visão geral do STAP". Revista IEEE Aerospace and Electronic Systems . 19 (1): 19–35. doi : 10.1109 / MAES.2004.1263229 .
• Röver, C. (2011). "Filtro baseado em t de Student para detecção de sinal robusta". Physical Review D . 84 (12): 122004. arXiv : 1109.0442 . Bibcode : 2011PhRvD..84l2004R . doi : 10.1103 / PhysRevD.84.122004 .
• Fish, A .; Gurevich, S .; Hadani, R .; Sayeed, A .; Schwartz, O. (dezembro de 2011). "Calculando o filtro combinado em tempo linear". arXiv : 1112.4883 [ cs.IT ].