Algoritmo QR - QR algorithm

Na álgebra linear numérica , o algoritmo QR ou iteração QR é um algoritmo de autovalor : isto é, um procedimento para calcular os autovalores e autovetores de uma matriz . O algoritmo QR foi desenvolvido no final dos anos 1950 por John GF Francis e por Vera N. Kublanovskaya , trabalhando de forma independente. A ideia básica é realizar uma decomposição QR , escrevendo a matriz como um produto de uma matriz ortogonal e uma matriz triangular superior , multiplicar os fatores na ordem inversa e iterar.

O algoritmo QR prático

Formalmente, seja Um ser uma verdadeira matriz do qual queremos calcular os valores próprios, e deixá- A ₀ : = A . No k -ésimo passo (começando com k = 0), calculamos a decomposição QR A _k = Q _k R _k onde Q _k é uma matriz ortogonal (ou seja, Q ^T = Q ⁻¹ ) e R _k é um triangular superior matriz. Em seguida, formamos A _{k +1} = R _k Q _k . Observe que

{\ displaystyle A_ {k + 1} = R_ {k} Q_ {k} = Q_ {k} ^ {- 1} Q_ {k} R_ {k} Q_ {k} = Q_ {k} ^ {- 1} A_ {k} Q_ {k} = Q_ {k} ^ {\ mathsf {T}} A_ {k} Q_ {k},}

portanto, todos os A _k são semelhantes e, portanto, têm os mesmos autovalores. O algoritmo é numericamente estável porque prossegue por transformações de similaridade ortogonal .

Sob certas condições, as matrizes Um _k convergem para uma matriz triangular, a forma de Schur de Uma . Os valores próprios de uma matriz triangular são listados na diagonal e o problema dos valores próprios é resolvido. No teste de convergência, é impraticável exigir zeros exatos, mas o teorema do círculo de Gershgorin fornece um limite para o erro.

Nessa forma bruta, as iterações são relativamente caras. Isso pode ser mitigado trazendo primeiro a matriz A para a forma Hessenberg superior (que custa operações aritméticas usando uma técnica baseada na redução de Householder ), com uma sequência finita de transformações de similaridade ortogonal, algo como uma decomposição QR de dois lados. (Para decomposição QR, os refletores Householder são multiplicados apenas à esquerda, mas para o caso de Hessenberg eles são multiplicados tanto à esquerda quanto à direita.) Determinar a decomposição QR de uma matriz de Hessenberg superior custa operações aritméticas. Além disso, como a forma de Hessenberg já é quase triangular superior (ela tem apenas uma entrada diferente de zero abaixo de cada diagonal), usá-la como ponto de partida reduz o número de etapas necessárias para a convergência do algoritmo QR. ${\ displaystyle {\ begin {matrix} {\ frac {10} {3}} \ end {matrix}} n ^ {3} + {\ mathcal {O}} (n ^ {2})}$ ${\ displaystyle 6n ^ {2} + {\ mathcal {O}} (n)}$

Se a matriz original for simétrica , então a matriz superior de Hessenberg também é simétrica e, portanto , tridiagonal , e assim são todos os A _k . Este procedimento custa operações aritméticas usando uma técnica baseada na redução de Householder. Determinar a decomposição QR de operações de custos de uma matriz tridiagonal simétrica . ${\ displaystyle {\ begin {matrix} {\ frac {4} {3}} \ end {matrix}} n ^ {3} + {\ mathcal {O}} (n ^ {2})}$ ${\ displaystyle {\ mathcal {O}} (n)}$

A taxa de convergência depende da separação entre os autovalores, portanto, um algoritmo prático usará deslocamentos, explícitos ou implícitos, para aumentar a separação e acelerar a convergência. Um algoritmo QR simétrico típico isola cada valor próprio (em seguida, reduz o tamanho da matriz) com apenas uma ou duas iterações, tornando-o eficiente e robusto.

Visualização

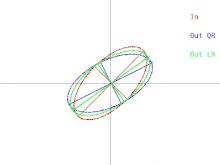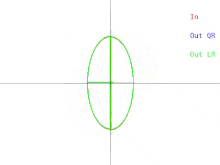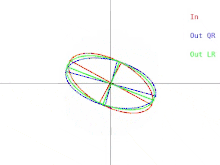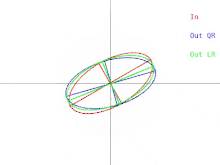
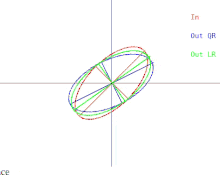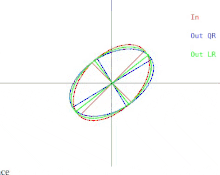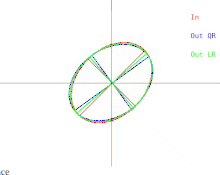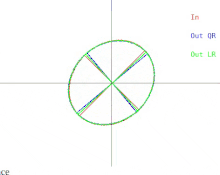
Figura 1: Como a saída de uma única iteração do algoritmo QR ou LR varia ao longo de sua entrada

O algoritmo QR básico pode ser visualizado no caso em que A é uma matriz simétrica definida positiva. Nesse caso, A pode ser representado como uma elipse em 2 dimensões ou um elipsóide em dimensões superiores. O relacionamento entre a entrada para o algoritmo e uma única iteração pode então ser descrito como na Figura 1 (clique para ver uma animação). Observe que o algoritmo LR é representado junto com o algoritmo QR.

Uma única iteração faz com que a elipse se incline ou "caia" em direção ao eixo x. No caso em que o grande semieixo da elipse é paralelo ao eixo x, uma iteração de QR não faz nada. Outra situação em que o algoritmo "não faz nada" é quando o semieixo grande é paralelo ao eixo y em vez do eixo x. Nesse caso, pode-se pensar que a elipse está se equilibrando precariamente, sem ser capaz de cair em nenhuma direção. Em ambas as situações, a matriz é diagonal. Uma situação em que uma iteração do algoritmo "não faz nada" é chamada de ponto fixo . A estratégia empregada pelo algoritmo é a iteração em direção a um ponto fixo . Observe que um ponto fixo é estável enquanto o outro é instável. Se a elipse fosse inclinada para longe do ponto fixo instável por uma quantidade muito pequena, uma iteração de QR faria com que a elipse se inclinasse para longe do ponto fixo em vez de na direção. Porém, eventualmente, o algoritmo convergiria para um ponto fixo diferente, mas levaria muito tempo.

Encontrar autovalores versus encontrar autovetores

Figura 2: Como a saída de uma única iteração de QR ou LR é afetada quando dois valores próprios se aproximam

De imediato, vale a pena apontar que encontrar até mesmo um único autovetor de uma matriz simétrica é incomputável (em aritmética real exata de acordo com as definições em análise computável ). Essa dificuldade existe sempre que as multiplicidades dos autovalores de uma matriz não são cognoscíveis. Por outro lado, o mesmo problema não existe para encontrar autovalores. Os valores próprios de uma matriz são sempre computáveis.

Vamos agora discutir como essas dificuldades se manifestam no algoritmo QR básico. Isso é ilustrado na Figura 2. (Lembre-se de clicar na miniatura). Lembre-se de que as elipses representam matrizes simétricas definidas positivas. Conforme os dois valores próprios da matriz de entrada se aproximam, a elipse de entrada se transforma em um círculo. Um círculo corresponde a um múltiplo da matriz identidade. Um círculo próximo corresponde a um quase múltiplo da matriz de identidade cujos autovalores são quase iguais às entradas diagonais da matriz. Portanto, o problema de encontrar aproximadamente os autovalores se mostra fácil nesse caso. Mas observe o que acontece com os semieixos das elipses. Uma iteração de QR (ou LR) inclina os semieixos cada vez menos conforme a elipse de entrada se aproxima de um círculo. Os autovetores só podem ser conhecidos quando os semieixos são paralelos aos eixos xey. O número de iterações necessárias para atingir o quase paralelismo aumenta sem limites à medida que a elipse de entrada se torna mais circular.

Embora possa ser impossível calcular a decomposição automática de uma matriz simétrica arbitrária, é sempre possível perturbar a matriz por uma quantidade arbitrariamente pequena e calcular a decomposição automática da matriz resultante. No caso em que a matriz é representada como um círculo próximo, a matriz pode ser substituída por outra cuja representação seja um círculo perfeito. Nesse caso, a matriz é um múltiplo da matriz identidade e sua decomposição automática é imediata. Esteja ciente de que embora o resultado eigenbasis pode ser muito longe da eigenbasis originais.

O algoritmo QR implícito

Na prática computacional moderna, o algoritmo QR é executado em uma versão implícita que torna o uso de vários turnos mais fácil de introduzir. A matriz é primeiro trazida para a forma de Hessenberg superior como na versão explícita; então, em cada etapa, a primeira coluna de é transformada por meio de uma transformação de similaridade de Householder de tamanho pequeno para a primeira coluna de (ou ), onde , de grau , é o polinômio que define a estratégia de deslocamento (frequentemente , onde e são os dois autovalores da submatriz principal posterior de , o chamado deslocamento duplo implícito ). Em seguida, sucessivas transformações de Householder de tamanho são realizadas a fim de retornar a matriz de trabalho à forma de Hessenberg superior. Esta operação é conhecida como perseguição de protuberâncias , devido à forma peculiar das entradas diferentes de zero da matriz ao longo das etapas do algoritmo. Como na primeira versão, a deflação é realizada assim que uma das entradas sub-diagonais de for suficientemente pequena. ${\ displaystyle A_ {0} = QAQ ^ {\ mathsf {T}}}$ ${\ displaystyle A_ {k}}$ ${\ displaystyle p (A_ {k})}$ ${\ displaystyle p (A_ {k}) e_ {1}}$ ${\ displaystyle p (A_ {k})}$ ${\ displaystyle r}$ ${\ displaystyle p (x) = (x- \ lambda) (x - {\ bar {\ lambda}})}$ ${\ displaystyle \ lambda}$ ${\ displaystyle {\ bar {\ lambda}}}$ ${\ displaystyle 2 \ vezes 2}$ ${\ displaystyle A_ {k}}$ ${\ displaystyle r + 1}$ ${\ displaystyle A_ {k}}$ ${\ displaystyle A_ {k}}$

Proposta de renomeação

Como na versão implícita moderna do procedimento nenhuma decomposição QR é explicitamente executada, alguns autores, por exemplo Watkins, sugeriram alterar seu nome para algoritmo de Francis . Golub e Van Loan usam o termo etapa Francis de QR .

Interpretação e convergência

O algoritmo QR pode ser visto como uma variação mais sofisticada do algoritmo de autovalor básico de "potência" . Lembre-se de que o algoritmo de potência multiplica repetidamente A vezes um único vetor, normalizando após cada iteração. O vetor converge para um autovetor do maior autovalor. Em vez disso, o algoritmo QR funciona com uma base completa de vetores, usando a decomposição QR para renormalizar (e ortogonalizar). Para uma matriz simétrica A , na convergência, AQ = QΛ , onde Λ é a matriz diagonal dos autovalores para os quais A convergiu, e onde Q é um composto de todas as transformadas de similaridade ortogonal necessárias para chegar lá. Assim, as colunas de Q são os autovetores.

História

O algoritmo QR foi precedido pelo algoritmo LR , que usa a decomposição LU em vez da decomposição QR. O algoritmo QR é mais estável, então o algoritmo LR raramente é usado hoje em dia. No entanto, representa uma etapa importante no desenvolvimento do algoritmo QR.

O algoritmo LR foi desenvolvido no início dos anos 1950 por Heinz Rutishauser , que trabalhava na época como assistente de pesquisa de Eduard Stiefel na ETH Zurich . Stiefel sugerido que Rutishauser usar a sequência de momentos y ₀^T A ^K x ₀ , k = 0, 1, ... (em que x ₀ e y ₀ são vectores arbitrárias) para encontrar os valores próprios de uma . Rutishauser pegou um algoritmo de Alexander Aitken para essa tarefa e o desenvolveu no algoritmo de diferença de quociente ou algoritmo qd . Depois de organizar o cálculo em uma forma adequada, ele descobriu que o algoritmo qd é na verdade a iteração A _k = L _k U _k (decomposição LU), A _{k +1} = U _k L _k , aplicada em uma matriz tridiagonal, a partir da qual segue o algoritmo LR.

Outras variantes

Uma variante do algoritmo QR , o algoritmo Golub-Kahan-Reinsch começa com a redução de uma matriz geral em uma matriz bidiagonal. Esta variante do algoritmo QR para o cálculo de valores singulares foi descrita pela primeira vez por Golub & Kahan (1965) . A sub-rotina LAPACK DBDSQR implementa este método iterativo, com algumas modificações para cobrir o caso em que os valores singulares são muito pequenos ( Demmel & Kahan 1990 ) . Junto com uma primeira etapa usando reflexões de Householder e, se apropriado, decomposição QR , isso forma a rotina DGESVD para o cálculo da decomposição de valor singular . O algoritmo QR também pode ser implementado em dimensões infinitas com resultados de convergência correspondentes.

Languages

In other projects