Geometria de distância - Distance geometry

A geometria da distância é a caracterização e o estudo de conjuntos de pontos com base apenas em determinados valores das distâncias entre pares de barras. Mais abstratamente, é o estudo de espaços semimétricos e as transformações isométricas entre eles. Nessa visão, pode ser considerado um assunto dentro da topologia geral .

Historicamente, o primeiro resultado em geometria de distância é a fórmula de Heron no século 1 DC. A teoria moderna começou no século 19 com o trabalho de Arthur Cayley , seguido por desenvolvimentos mais extensos no século 20 por Karl Menger e outros.

Problemas de geometria de distâncias surgem sempre que se precisa inferir a forma de uma configuração de pontos ( posições relativas ) a partir das distâncias entre eles, como em biologia , rede de sensores , levantamento topográfico , navegação , cartografia e física .

Introdução e definições

Os conceitos de geometria de distância serão explicados primeiro pela descrição de dois problemas particulares.

Primeiro problema: navegação hiperbólica

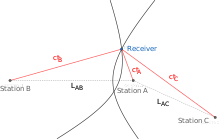
Considere três estações de rádio terrestres A, B, C, cujas localizações são conhecidas. Um receptor de rádio está em um local desconhecido. O tempo que leva para um sinal de rádio viajar das estações para o receptor,, são desconhecidos, mas as diferenças de tempo, e , são conhecidas. A partir deles, sabe-se as diferenças de distância e , de onde pode ser encontrada a posição do receptor. ${\ displaystyle t_ {A}, t_ {B}, t_ {C}}$${\ displaystyle t_ {A} -t_ {B}}$${\ displaystyle t_ {A} -t_ {C}}$${\ displaystyle c (t_ {A} -t_ {B})}$${\ displaystyle c (t_ {A} -t_ {C})}$

Segundo problema: redução de dimensão

Na análise de dados , geralmente é fornecida uma lista de dados representados como vetores e é necessário descobrir se eles estão dentro de um subespaço afim de baixa dimensão. Uma representação de dados de baixa dimensão tem muitas vantagens, como economizar espaço de armazenamento, tempo de computação e fornecer uma visão melhor dos dados. ${\ displaystyle \ mathbf {v} = (x_ {1}, \ ldots, x_ {n}) \ in \ mathbb {R} ^ {n}}$

Definições

Agora formalizamos algumas definições que surgem naturalmente da consideração de nossos problemas.

Espaço semimétrico

Dada uma lista de pontos sobre , podemos arbitrariamente especificar as distâncias entre pares de pontos por uma lista de , . Isso define um espaço semimétrico : um espaço métrico sem desigualdade triangular . ${\ displaystyle R = \ {P_ {0}, \ ldots, P_ {n} \}}$${\ displaystyle n \ geq 0}$${\ displaystyle d_ {ij}> 0}$${\ displaystyle 0 \ leq i <j \ leq n}$

Explicitamente, definimos um espaço semimétrico como um conjunto não vazio equipado com um semimétrico tal que, para todos , ${\ displaystyle R}$${\ displaystyle d: R \ times R \ to [0, \ infty)}$${\ displaystyle x, y \ in R}$

1. Positividade:   se e somente se   .${\ displaystyle d (x, y) = 0}$${\ displaystyle x = y}$
2. Simetria: .${\ displaystyle d (x, y) = d (y, x)}$

Qualquer espaço métrico é, a fortiori, um espaço semimétrico. Em particular, o espaço euclidiano -dimensional , é o espaço métrico canônico em geometria de distância. ${\ displaystyle \ mathbb {R} ^ {k}}$${\ displaystyle k}$

A desigualdade do triângulo é omitida na definição, porque não queremos impor mais restrições às distâncias do que o mero requisito de que sejam positivas. ${\ displaystyle d_ {ij}}$

Na prática, os espaços semimétricos surgem naturalmente de medições imprecisas. Por exemplo, dados três pontos em uma linha, com , uma medição imprecisa poderia dar , violando a desigualdade do triângulo. ${\ displaystyle A, B, C}$${\ displaystyle d_ {AB} = 1, d_ {BC} = 1, d_ {AC} = 2}$${\ displaystyle d_ {AB} = 0,99, d_ {BC} = 0,98, d_ {AC} = 2,00}$

Incorporação isométrica

Dados dois espaços semimetric, , uma incorporação isométrica a partir de um mapa que preserva a semimetric, isto é, para todos , . ${\ displaystyle (R, d), (R ', d')}$${\ displaystyle R}$${\ displaystyle R '}$${\ displaystyle f: R \ para R '}$${\ displaystyle x, y \ in R}$${\ displaystyle d (x, y) = d '(f (x), f (y))}$

Por exemplo, dado o espaço semimétrico finito definido acima, um embedding isométrico em é definido por pontos , de modo que para todos . ${\ displaystyle (R, d)}$${\ textstyle A_ {0}, A_ {1}, \ ldots, A_ {n} \ in \ mathbb {R} ^ {k}}$${\ displaystyle d (A_ {i}, A_ {j}) = d_ {ij}}$${\ displaystyle 0 \ leq i <j \ leq n}$

Independência afim

Dados os pontos , eles são definidos para serem independentes por afinidade , se não puderem caber dentro de um subespaço afim unidimensional de , para nenhum , se o - simplex que abrangem ,, tiver volume positivo , isto é ,. ${\ textstyle A_ {0}, A_ {1}, \ ldots, A_ {n} \ in \ mathbb {R} ^ {k}}$${\ displaystyle l}$${\ displaystyle \ mathbb {R} ^ {k}}$${\ displaystyle \ ell <n}$${\ displaystyle n}$${\ displaystyle v_ {n}}$${\ displaystyle n}$${\ displaystyle \ operatorname {Vol} _ {n} (v_ {n})> 0}$

Em geral, quando , eles são independentes por afinidade, uma vez que um n -simplex genérico não é degenerado. Por exemplo, 3 pontos no plano, em geral, não são colineares, porque o triângulo que eles abrangem não degenera em um segmento de linha. Da mesma forma, 4 pontos no espaço, em geral, não são coplanares, porque o tetraedro que abrangem não degenera em um triângulo plano. ${\ displaystyle k \ geq n}$

Quando , eles devem ser afinamente dependentes. Isso pode ser visto observando que qualquer -simplex que possa caber dentro deve ser "plano". ${\ displaystyle n> k}$${\ displaystyle n}$${\ displaystyle \ mathbb {R} ^ {k}}$

Determinantes de Cayley-Menger

Os determinantes de Cayley-Menger , em homenagem a Arthur Cayley e Karl Menger, são determinantes de matrizes de distâncias entre conjuntos de pontos.

Let ser n  + 1 pontos num espaço semimetric, o seu determinante Cayley-Menger é definida pela ${\ textstyle A_ {0}, A_ {1}, \ ldots, A_ {n}}$

${\ displaystyle \ operatorname {CM} (A_ {0}, \ cdots, A_ {n}) = {\ begin {vmatrix} 0 & d_ {01} ^ {2} & d_ {02} ^ {2} & \ cdots & d_ { 0n} ^ {2} & 1 \\ d_ {01} ^ {2} & 0 & d_ {12} ^ {2} & \ cdots & d_ {1n} ^ {2} & 1 \\ d_ {02} ^ {2} & d_ {12 } ^ {2} & 0 & \ cdots & d_ {2n} ^ {2} & 1 \\\ vdots & \ vdots & \ vdots & \ ddots & \ vdots & \ vdots \\ d_ {0n} ^ {2} & d_ {1n} ^ {2} & d_ {2n} ^ {2} & \ cdots & 0 & 1 \\ 1 & 1 & 1 & \ cdots & 1 & 0 \ end {vmatrix}}}$

Se , então eles formam os vértices de um (possivelmente degenerado ) n -simplex em . Pode-se mostrar que o volume n- dimensional do simplex satisfaz ${\ textstyle A_ {0}, A_ {1}, \ ldots, A_ {n} \ in \ mathbb {R} ^ {k}}$${\ displaystyle v_ {n}}$${\ displaystyle \ mathbb {R} ^ {k}}$${\ displaystyle v_ {n}}$

${\ displaystyle \ operatorname {Vol} _ {n} (v_ {n}) ^ {2} = {\ frac {(-1) ^ {n + 1}} {(n!) ^ {2} 2 ^ { n}}} \ operatorname {CM} (A_ {0}, \ ldots, A_ {n}).}$

Observe que, para o caso de , temos , significando que o "volume 0-dimensional" de um simplex 0 é 1, ou seja, há 1 ponto em um simplex 0. ${\ displaystyle n = 0}$${\ displaystyle \ operatorname {Vol} _ {0} (v_ {0}) = 1}$

${\ textstyle A_ {0}, A_ {1}, \ ldots, A_ {n}}$são afinamente independentes iff , isto é ,. Assim, os determinantes de Cayley-Menger fornecem uma maneira computacional de provar a independência afim. ${\ displaystyle \ operatorname {Vol} _ {n} (v_ {n})> 0}$${\ displaystyle (-1) ^ {n + 1} \ operatorname {CM} (A_ {0}, \ ldots, A_ {n})> 0}$

Se , então, os pontos devem ser afinamente dependentes, portanto . O artigo de Cayley de 1841 estudou o caso especial de , isto é, quaisquer cinco pontos no espaço tridimensional devem ter . ${\ displaystyle k <n}$${\ displaystyle \ operatorname {CM} (A_ {0}, \ ldots, A_ {n}) = 0}$${\ displaystyle k = 3, n = 4}$${\ displaystyle A_ {0}, \ ldots, A_ {4}}$${\ displaystyle \ operatorname {CM} (A_ {0}, \ ldots, A_ {4}) = 0}$

História

O primeiro resultado em geometria de distância é a fórmula de Heron , do século I DC, que dá a área de um triângulo a partir das distâncias entre seus 3 vértices. A fórmula de Brahmagupta , do século 7 DC, generaliza para quadriláteros cíclicos . Tartaglia , do século 16 DC, generalizou-o para dar o volume do tetraedro a partir das distâncias entre seus 4 vértices.

A teoria moderna da geometria da distância começou com Authur Cayley e Karl Menger . Cayley publicou o determinante Cayley em 1841, que é um caso especial do determinante Cayley-Menger geral. Menger provou em 1928 um teorema de caracterização de todos os espaços semimétricos que são isometricamente embutidos no espaço euclidiano n- dimensional . Em 1931, Menger usou relações de distância para dar um tratamento axiomático da geometria euclidiana. ${\ displaystyle \ mathbb {R} ^ {n}}$

O livro de Leonard Blumenthal oferece uma visão geral da geometria à distância no nível de graduação, uma grande parte da qual é tratada em inglês pela primeira vez quando foi publicado.

Teorema de caracterização de Menger

Menger provou o seguinte teorema de caracterização de espaços semimétricos:

Um espaço semimétrico é isometricamente incorporável no espaço euclidiano dimensional , mas não em nenhum , se e somente se: ${\ displaystyle (R, d)}$${\ displaystyle n}$${\ displaystyle \ mathbb {R} ^ {n}}$${\ displaystyle \ mathbb {R} ^ {m}}$${\ displaystyle 0 \ leq m <n}$

1. ${\ displaystyle R}$contém um subconjunto de pontos que é isométrico com um subconjunto de pontos independentes afinamente de ;${\ displaystyle (n + 1)}$${\ displaystyle S}$${\ displaystyle (n + 1)}$${\ displaystyle \ mathbb {R} ^ {n}}$
2. qualquer subconjunto de pontos , obtido pela adição de quaisquer dois pontos adicionais de a , é congruente a um subconjunto de pontos de .${\ displaystyle (n + 3)}$${\ displaystyle S '}$${\ displaystyle R}$${\ displaystyle S}$${\ displaystyle (n + 3)}$${\ displaystyle \ mathbb {R} ^ {n}}$

Uma prova desse teorema em uma forma ligeiramente enfraquecida (para espaços métricos em vez de espaços semimétricos) está em.

Caracterização via determinantes de Cayley-Menger

Os resultados a seguir são comprovados no livro de Blumethal.

Pontos de incorporação em${\ displaystyle n + 1}$${\ displaystyle \ mathbb {R} ^ {n}}$

Dado um espaço semimetric , com , e , , uma incorporação de isométrica em é definido por , de tal modo que para todos . ${\ displaystyle (S, d)}$${\ displaystyle S = \ {P_ {0}, \ ldots, P_ {n} \}}$${\ displaystyle d (P_ {i}, P_ {j}) = d_ {ij} \ geq 0}$${\ displaystyle 0 \ leq i <j \ leq n}$${\ displaystyle (S, d)}$${\ displaystyle \ mathbb {R} ^ {n}}$${\ textstyle A_ {0}, A_ {1}, \ ldots, A_ {n} \ in \ mathbb {R} ^ {n}}$${\ displaystyle d (A_ {i}, A_ {j}) = d_ {ij}}$${\ displaystyle 0 \ leq i <j \ leq n}$

Novamente, alguém pergunta se tal incorporação isométrica existe para . ${\ displaystyle (S, d)}$

Uma condição necessária é fácil de ver: para todos , seja o k- simples formado por , então ${\ displaystyle k = 1, \ ldots, n}$${\ displaystyle v_ {k}}$${\ textstyle A_ {0}, A_ {1}, \ ldots, A_ {k}}$

${\ displaystyle (-1) ^ {k + 1} \ operatorname {CM} (P_ {0}, \ ldots, P_ {k}) = (- 1) ^ {k + 1} \ operatorname {CM} (A_ {0}, \ ldots, A_ {k}) = 2 ^ {k} (k!) ^ {K} \ operatorname {Vol} _ {k} (v_ {k}) ^ {2} \ geq 0}$

O inverso também é válido. Ou seja, se para todos , ${\ displaystyle k = 1, \ ldots, n}$

${\ displaystyle (-1) ^ {k + 1} \ operatorname {CM} (P_ {0}, \ ldots, P_ {k}) \ geq 0,}$

então tal incorporação existe.

Além disso, tal incorporação é exclusiva até a isometria em . Ou seja, dados quaisquer dois embeddings isométricos definidos por , e , existe uma isometria (não necessariamente única) , tal que para todos . Tal é único se e somente se , isto é, forem afinamente independentes. ${\ displaystyle \ mathbb {R} ^ {n}}$${\ textstyle A_ {0}, A_ {1}, \ ldots, A_ {n}}$${\ textstyle A '_ {0}, A' _ {1}, \ ldots, A '_ {n}}$${\ displaystyle T: \ mathbb {R} ^ {n} \ to \ mathbb {R} ^ {n}}$${\ displaystyle T (A_ {k}) = A '_ {k}}$${\ displaystyle k = 0, \ ldots, n}$${\ displaystyle T}$${\ displaystyle \ operatorname {CM} (P_ {0}, \ ldots, P_ {n}) \ neq 0}$${\ textstyle A_ {0}, A_ {1}, \ ldots, A_ {n}}$

Incorporação e pontos${\ displaystyle n + 2}$${\ displaystyle n + 3}$

Se os pontos podem ser incorporados como , então diferente das condições acima, uma condição necessária adicional é que o -simplex formado por , deve ter um volume não -dimensional. Ou seja ,. ${\ displaystyle n + 2}$${\ displaystyle P_ {0}, \ ldots, P_ {n + 1}}$${\ displaystyle \ mathbb {R} ^ {n}}$${\ displaystyle A_ {0}, \ ldots, A_ {n + 1}}$${\ displaystyle (n + 1)}$${\ textstyle A_ {0}, A_ {1}, \ ldots, A_ {n + 1}}$${\ displaystyle (n + 1)}$${\ displaystyle \ operatorname {CM} (P_ {0}, \ ldots, P_ {n}, P_ {n + 1}) = 0}$

O inverso também é válido. Ou seja, se para todos , ${\ displaystyle k = 1, \ ldots, n}$

${\ displaystyle (-1) ^ {k + 1} \ operatorname {CM} (P_ {0}, \ ldots, P_ {k}) \ geq 0,}$

e

${\ displaystyle \ operatorname {CM} (P_ {0}, \ ldots, P_ {n}, P_ {n + 1}) = 0,}$

então tal incorporação existe.

Para pontos de incorporação em , as condições necessárias e suficientes são semelhantes: ${\ displaystyle n + 3}$${\ displaystyle \ mathbb {R} ^ {n}}$

1. Para todos , ;${\ displaystyle k = 1, \ ldots, n}$${\ displaystyle (-1) ^ {k + 1} \ operatorname {CM} (P_ {0}, \ ldots, P_ {k}) \ geq 0}$
2. ${\ displaystyle \ operatorname {CM} (P_ {0}, \ ldots, P_ {n}, P_ {n + 1}) = 0;}$
3. ${\ displaystyle \ operatorname {CM} (P_ {0}, \ ldots, P_ {n}, P_ {n + 2}) = 0;}$
4. ${\ displaystyle \ operatorname {CM} (P_ {0}, \ ldots, P_ {n}, P_ {n + 1}, P_ {n + 2}) = 0.}$

Incorporando muitos pontos arbitrariamente

O caso acaba sendo suficiente em geral. ${\ displaystyle n + 3}$

Em geral, dado um espaço semimetric , ele pode ser isometrically embutido se e somente se existe , de tal forma que, para todos , e para qualquer , ${\ displaystyle (R, d)}$${\ displaystyle \ mathbb {R} ^ {n}}$${\ displaystyle P_ {0}, \ ldots, P_ {n} \ in R}$${\ displaystyle k = 1, \ ldots, n}$${\ displaystyle (-1) ^ {k + 1} \ operatorname {CM} (P_ {0}, \ ldots, P_ {k}) \ geq 0}$${\ displaystyle P_ {n + 1}, P_ {n + 2} \ in R}$

1. ${\ displaystyle \ operatorname {CM} (P_ {0}, \ ldots, P_ {n}, P_ {n + 1}) = 0;}$
2. ${\ displaystyle \ operatorname {CM} (P_ {0}, \ ldots, P_ {n}, P_ {n + 2}) = 0;}$
3. ${\ displaystyle \ operatorname {CM} (P_ {0}, \ ldots, P_ {n}, P_ {n + 1}, P_ {n + 2}) = 0.}$

E essa incorporação é exclusiva até a isometria em . ${\ displaystyle \ mathbb {R} ^ {n}}$

Além disso, se , então ele não pode ser isometricamente embutido em nenhum . E tal incorporação é única até a isometria única em . ${\ displaystyle \ operatorname {CM} (P_ {0}, \ ldots, P_ {n}) \ neq 0}$${\ displaystyle \ mathbb {R} ^ {m}, m <n}$${\ displaystyle \ mathbb {R} ^ {n}}$

Assim, os determinantes de Cayley-Menger fornecem uma maneira concreta de calcular se um espaço semimétrico pode ser embutido , para alguns finitos e, em caso afirmativo, qual é o mínimo . ${\ displaystyle \ mathbb {R} ^ {n}}$${\ displaystyle n}$${\ displaystyle n}$

Formulários

Existem muitas aplicações da geometria de distância.

Em redes de telecomunicações como o GPS , são conhecidas as posições de alguns sensores (chamados de âncoras) e também são conhecidas algumas das distâncias entre os sensores: o problema é identificar as posições de todos os sensores. A navegação hiperbólica é uma tecnologia pré-GPS que usa geometria de distância para localizar navios com base no tempo que os sinais levam para alcançar as âncoras.

Existem muitas aplicações em química. Técnicas como RMN podem medir distâncias entre pares de átomos de uma determinada molécula, e o problema é inferir a forma tridimensional da molécula a partir dessas distâncias.

Alguns pacotes de software para aplicativos são:

• DGSOL . Resolve problemas de geometria de grandes distâncias na modelagem macromolecular .
• Xplor-NIH . Com base em X-PLOR , para determinar a estrutura das moléculas com base em dados de experimentos de NMR. Ele resolve problemas de geometria de distância com métodos heurísticos (como recozimento simulado ) e métodos de pesquisa local (como minimização de gradiente conjugado ).
• TINKER . Modelagem e design molecular. Ele pode resolver problemas de geometria de distância.
• SNLSDPclique . Código MATLAB para localização de sensores em uma rede de sensores com base nas distâncias entre os sensores.

Veja também

• Matriz de distância euclidiana
• Escala multidimensional (uma técnica estatística usada quando as distâncias são medidas com erros aleatórios)
• Espaço métrico
• Fórmula de Tartaglia
• Triangulação
• Trilateração

Referências