Ladrilhos dominó - Domino tiling

Uma telha de dominó de um quadrado 8 × 8

Em geometria , o dominó de uma região do plano euclidiano é uma tesselação da região por dominós , formas formadas pela união de dois quadrados unitários que se encontram de ponta a ponta. Equivalentemente, é um casamento perfeito no gráfico de grade formado pela colocação de um vértice no centro de cada quadrado da região e conectando dois vértices quando eles correspondem a quadrados adjacentes.

Funções de altura

Para algumas classes de tilings em uma grade regular em duas dimensões, é possível definir uma função de altura associando um inteiro aos vértices da grade. Por exemplo, desenhe um tabuleiro de xadrez, fixe um nó com altura 0, então para qualquer nó há um caminho de até ele. Neste caminho, defina a altura de cada nó (ou seja, cantos dos quadrados) como sendo a altura do nó anterior mais um se o quadrado à direita do caminho de a for preto e menos um caso contrário. ${\ displaystyle A_ {0}}$${\ displaystyle A_ {0}}$${\ displaystyle A_ {n + 1}}$${\ displaystyle A_ {n}}$${\ displaystyle A_ {n}}$${\ displaystyle A_ {n + 1}}$

Mais detalhes podem ser encontrados em Kenyon & Okounkov (2005) .

Condição de altura de Thurston

William Thurston  ( 1990 ) descreve um teste para determinar se uma região simplesmente conectada, formada como a união de quadrados unitários no plano, tem um mosaico de dominó. Ele forma um gráfico não direcionado que tem como vértices os pontos ( x , y , z ) na rede inteira tridimensional , onde cada um desses pontos está conectado a quatro vizinhos: se x  +  y for par, então ( x , y , z ) está conectado a ( x  + 1, y , z  + 1), ( x  - 1, y , z  + 1), ( x , y  + 1, z  - 1) e ( x , y  - 1, z  - 1), enquanto se x  +  y for ímpar, então ( x , y , z ) está conectado a ( x  + 1, y , z  - 1), ( x  - 1, y , z  - 1), ( x , y  + 1, z  + 1) e ( x , y  - 1, z  + 1). O limite da região, visto como uma sequência de pontos inteiros no plano ( x , y ), eleva-se exclusivamente (uma vez que uma altura inicial é escolhida) para um caminho neste gráfico tridimensional . Uma condição necessária para que essa região seja inclinada é que esse caminho deva se fechar para formar uma curva fechada simples em três dimensões, porém, essa condição não é suficiente. Usando uma análise mais cuidadosa do caminho de limite, Thurston forneceu um critério de capacidade de tilização de uma região que era suficiente e também necessário.

Contando tilings de regiões

Um mosaico de dominó de um quadrado de 8 × 8 usando o número mínimo de pares de borda longa a borda longa (1 par no centro). Este arranjo também é um mosaico de tatami válido de um quadrado de 8x8, sem quatro dominós se tocando em um ponto interno.

O número de maneiras de cobrir um retângulo com dominó, calculado independentemente por Temperley & Fisher (1961) e Kasteleyn (1961) , é dado por ${\ displaystyle m \ times n}$${\ displaystyle {\ frac {mn} {2}}}$

${\ displaystyle \ prod _ {j = 1} ^ {\ lceil {\ frac {m} {2}} \ rceil} \ prod _ {k = 1} ^ {\ lceil {\ frac {n} {2}} \ rceil} \ left (4 \ cos ^ {2} {\ frac {\ pi j} {m + 1}} + 4 \ cos ^ {2} {\ frac {\ pi k} {n + 1}} \ direito).}$

Quando ambos m e n são ímpares, a fórmula reduz corretamente a zero possíveis peças de dominó.

Um caso especial ocorre ao colocar lado a lado o retângulo com n dominós: a sequência se reduz à sequência de Fibonacci . ${\ displaystyle 2 \ vezes n}$

Outro caso especial acontece para quadrados com m = n = 0, 2, 4, 6, 8, 10, 12, ... é

1, 2, 36, 6728, 12988816, 258584046368, 53060477521960000, ... (sequência A004003 no OEIS ).

Esses números podem ser encontrados escrevendo-os como o Pfaffian de uma matriz assimétrica cujos autovalores podem ser encontrados explicitamente. Esta técnica pode ser aplicada em muitos assuntos relacionados à matemática, por exemplo, no cálculo clássico bidimensional da função de correlacionador dímero-dímero em mecânica estatística . ${\ displaystyle mn \ times mn}$

O número de inclinações de uma região é muito sensível às condições de contorno e pode mudar dramaticamente com mudanças aparentemente insignificantes na forma da região. Isso é ilustrado pelo número de tilings de um diamante asteca de ordem n , onde o número de tilings é 2 ^{( n  + 1) n / 2} . Se este for substituído pelo "diamante asteca aumentado" de ordem n com 3 longas filas no meio em vez de 2, o número de ladrilhos cai para o número muito menor D ( n , n ), um número de Delannoy , que tem apenas exponencial em vez de crescimento superexponencial em n . Para o "diamante asteca reduzido" de ordem n com apenas uma longa linha intermediária, há apenas um ladrilho.

• 

  Um diamante asteca de ordem 4, que tem 1.024 telhas de dominó

• 

  Um possível ladrilho

Tatami

Tatami são tapetes japoneses em forma de dominó (retângulo 1x2). Eles são usados ​​para revestir salas, mas com regras adicionais sobre como eles podem ser colocados. Em particular, normalmente, as junções onde três tatames se encontram são consideradas auspiciosas, enquanto as junções onde quatro se encontram são desfavoráveis, então uma telha de tatame adequada é aquela em que apenas três tatames se encontram em qualquer canto. um canto é NP-completo .

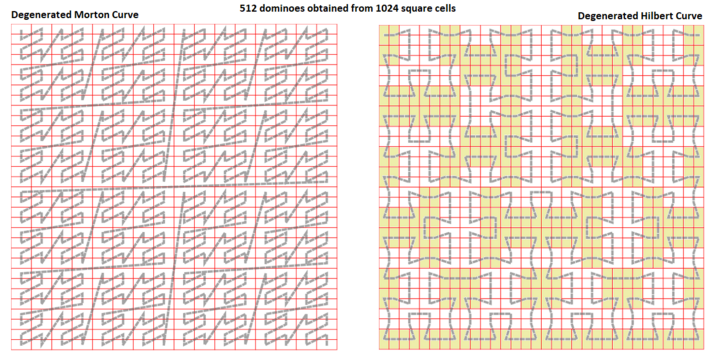
Curvas de preenchimento de espaço degeneradas

Qualquer conjunto finito de células formando grade quadrada regular n × n pode ser indexado por uma curva de preenchimento de espaço selecionada que é consistente com quadrados (que fazem uma partição recursiva de quatro da grade quadrilateral da unidade), com um índice i variando de 0 a n ² -1. Geometricamente, a curva pode ser desenhada como um caminho através do centro das células quadradas. Uma telha de dominó é obtida pela fusão de células vizinhas. O índice j de cada dominó será obtido pela função j = floor ( i  ÷  2) do índice da grade original. A nova curva fractal é uma "curva degenerada" porque é outro fractal. Exemplos:

A " curva degenerada de preenchimento do espaço de Morton " produz uma telha dominó regular com orientação horizontal; a curva está relacionada com a indexação Geohash , onde a curva em forma de Z é transformada em uma curva em forma de И.

A " curva de preenchimento espacial de Hilbert degenerada " produz um sistema de ladrilho aperiódico , misturando dominós de orientação horizontal e vertical, 50% de cada orientação. A curva de Hilbert degenerada é isomórfica ao fractal de Munkres.

Aplicações em física estatística

Há uma correspondência de um para um entre um mosaico periódico de dominó e uma configuração de estado fundamental do modelo de Ising totalmente frustrado em uma rede periódica bidimensional. Para ver isso, notamos que no estado fundamental, cada plaqueta do modelo de spin deve conter exatamente uma interação frustrada . Portanto, vendo a partir da rede dupla , cada aresta frustrada deve ser "coberta" por um retângulo 1x2 , de modo que os retângulos abrangem toda a rede e não se sobrepõem, ou um dominó da rede dupla.

Veja também

• Campo livre gaussiano , o limite de escala da função altura na situação genérica (por exemplo, dentro do disco inscrito de um grande diamante asteca)
• Problema do tabuleiro de xadrez mutilado , um quebra-cabeça relacionado ao jogo de dominó de um subconjunto de 62 quadrados do tabuleiro de xadrez
• Mecânica estatística

Notas

Referências

Leitura adicional