Método de Horner - Horner's method

Em matemática e ciência da computação , o método de Horner (ou esquema de Horner ) é um algoritmo para avaliação polinomial . Embora tenha o nome de William George Horner , este método é muito mais antigo, pois foi atribuído a Joseph-Louis Lagrange pelo próprio Horner, e pode remontar a muitas centenas de anos a matemáticos chineses e persas. Após a introdução dos computadores, esse algoritmo tornou-se fundamental para uma computação eficiente com polinômios.

O algoritmo é baseado na regra de Horner:

${\ displaystyle {\ begin {alinhados} a_ {0} & + a_ {1} x + a_ {2} x ^ {2} + a_ {3} x ^ {3} + \ cdots + a_ {n} x ^ {n} \\ & = a_ {0} + x {\ bigg (} a_ {1} + x {\ Big (} a_ {2} + x {\ big (} a_ {3} + \ cdots + x ( a_ {n-1} + x \, a_ {n}) \ cdots {\ big)} {\ Big)} {\ bigg)}. \ end {alinhado}}}$

Isso permite a avaliação de um polinômio de grau n com apenas multiplicações e adições. Isso é ótimo, uma vez que existem polinômios de grau n que não podem ser avaliados com menos operações aritméticas ${\ displaystyle n}$${\ displaystyle n}$

Alternativamente, o método de Horner também se refere a um método para aproximar as raízes de polinômios, descrito por Horner em 1819. É uma variante do método de Newton-Raphson tornado mais eficiente para cálculos manuais pela aplicação da regra de Horner. Foi amplamente utilizado até que os computadores se tornaram amplamente utilizados por volta de 1970.

Avaliação polinomial e divisão longa

Dado o polinômio

${\ displaystyle p (x) = \ sum _ {i = 0} ^ {n} a_ {i} x ^ {i} = a_ {0} + a_ {1} x + a_ {2} x ^ {2} + a_ {3} x ^ {3} + \ cdots + a_ {n} x ^ {n},}$

onde são coeficientes constantes, o problema é avaliar o polinômio em um valor específico de${\ displaystyle a_ {0}, \ ldots, a_ {n}}$${\ displaystyle x_ {0}}$${\ displaystyle x.}$

Para isso, uma nova sequência de constantes é definida recursivamente da seguinte forma:

${\ displaystyle {\ begin {alinhado} b_ {n} &: = a_ {n} \\ b_ {n-1} &: = a_ {n-1} + b_ {n} x_ {0} \\ (1 ) \ quad \ quad \ quad & ~~~ \ vdots \\ b_ {1} &: = a_ {1} + b_ {2} x_ {0} \\ b_ {0} &: = a_ {0} + b_ {1} x_ {0}. \ End {alinhado}}}$

Então é o valor de . ${\ displaystyle b_ {0}}$${\ displaystyle p (x_ {0})}$

Para ver por que isso funciona, o polinômio pode ser escrito na forma

${\ displaystyle p (x) = a_ {0} + x {\ bigg (} a_ {1} + x {\ Big (} a_ {2} + x {\ big (} a_ {3} + \ cdots + x (a_ {n-1} + x \, a_ {n}) \ cdots {\ big)} {\ Big)} {\ bigg)} \.}$

Assim, ao substituir iterativamente o na expressão, ${\ displaystyle b_ {i}}$

${\ displaystyle {\ begin {alinhados} p (x_ {0}) & = a_ {0} + x_ {0} {\ Big (} a_ {1} + x_ {0} {\ big (} a_ {2} + \ cdots + x_ {0} (a_ {n-1} + b_ {n} x_ {0}) \ cdots {\ big)} {\ Big)} \\ & = a_ {0} + x_ {0} {\ Big (} a_ {1} + x_ {0} {\ big (} a_ {2} + \ cdots + x_ {0} b_ {n-1} {\ big)} {\ Big)} \\ & ~~ \ vdots \\ & = a_ {0} + x_ {0} b_ {1} \\ & = b_ {0}. \ end {alinhado}}}$

Agora, pode ser provado isso;

${\ displaystyle (2) \ quad \ quad \ quad p (x) = (b_ {1} + b_ {2} x + b_ {3} x ^ {2} + b_ {4} x ^ {3} + \ cdots + b_ {n-1} x ^ {n-2} + b_ {n} x ^ {n-1}) (x-x_ {0}) + b_ {0}}$

Esta expressão constitui a aplicação prática de Horner, pois oferece uma maneira muito rápida de determinar o resultado de;

${\ displaystyle p (x) / (x-x_ {0})}$

com b ₀ (que é igual ap (x ₀ )) sendo o resto da divisão, como é demonstrado pelos exemplos abaixo. se x ₀ é a raiz de p (x), então b ₀ = 0 (significando que o resto é 0), o que significa que você pode fatorar p (x) com (xx ₀ ).
Quanto a encontrar os valores de b consecutivos, você começa determinando b _n , que é simplesmente igual a a _n . Em seguida, você desce até os outros b's, usando a fórmula;

${\ displaystyle b_ {n-1} = a_ {n-1} + b_ {n} x_ {0}}$

até você chegar em b ₀ .

Exemplos

Avalie para${\ displaystyle f (x) = 2x ^ {3} -6x ^ {2} + 2x-1}$${\ displaystyle x = 3.}$

Usamos a divisão sintética da seguinte forma:

 x0│   x3    x2    x1    x0
 3 │   2    −6     2    −1
   │         6     0     6
   └────────────────────────
       2     0     2     5

As entradas na terceira linha são a soma das duas primeiras. Cada entrada na segunda linha é o produto do valor x (3 neste exemplo) com a entrada da terceira linha imediatamente à esquerda. As entradas na primeira linha são os coeficientes do polinômio a ser avaliado. Então, o resto da divisão por é 5. ${\ displaystyle f (x)}$${\ displaystyle x-3}$

Mas pelo teorema do resto polinomial , sabemos que o resto é . Assim${\ displaystyle f (3)}$${\ displaystyle f (3) = 5}$

Neste exemplo, se podemos ver isso , as entradas na terceira linha. Portanto, a divisão sintética é baseada no método de Horner. ${\ displaystyle a_ {3} = 2, a_ {2} = - 6, a_ {1} = 2, a_ {0} = - 1}$${\ displaystyle b_ {3} = 2, b_ {2} = 0, b_ {1} = 2, b_ {0} = 5}$

Como consequência do teorema do resto do polinômio, as entradas na terceira linha são os coeficientes do polinômio de segundo grau, o quociente de na divisão por . O restante é 5. Isso torna o método de Horner útil para a divisão longa polinomial . ${\ displaystyle f (x)}$${\ displaystyle x-3}$

Dividir por : ${\ displaystyle x ^ {3} -6x ^ {2} + 11x-6}$${\ displaystyle x-2}$

 2 │   1    −6    11    −6
   │         2    −8     6
   └────────────────────────
       1    −4     3     0

O quociente é . ${\ displaystyle x ^ {2} -4x + 3}$

Deixe e . Divida por usando o método de Horner. ${\ displaystyle f_ {1} (x) = 4x ^ {4} -6x ^ {3} + 3x-5}$${\ displaystyle f_ {2} (x) = 2x-1}$${\ displaystyle f_ {1} (x)}$${\ displaystyle f_ {2} \, (x)}$

  0.5 │ 4  -6   0   3  -5
      │     2  -2  -1   1
└───────────────────────
        2  -2  -1   1  -2

A terceira linha é a soma das duas primeiras linhas, dividida por 2. Cada entrada na segunda linha é o produto de 1 com a entrada da terceira linha à esquerda. A resposta é

${\ displaystyle {\ frac {f_ {1} (x)} {f_ {2} (x)}} = 2x ^ {3} -2x ^ {2} -x + 1 - {\ frac {4} {2x -1}}.}$

Eficiência

A avaliação usando a forma monomial de um polinômio grau n requer no máximo n adições e ( n ²  +  n ) / 2 multiplicações, se as potências forem calculadas por multiplicação repetida e cada monômio for avaliado individualmente. (Isso pode ser reduzido a n adições e 2 n  - 1 multiplicações avaliando as potências de x iterativamente.) Se os dados numéricos são representados em termos de dígitos (ou bits), então o algoritmo ingênuo também envolve o armazenamento de aproximadamente 2 n vezes o número de bits de x (o polinômio avaliado tem magnitude aproximada x ⁿ , e deve-se também armazenar o próprio x ⁿ ). Em contraste, o método de Horner requer apenas n adições en multiplicações, e seus requisitos de armazenamento são apenas n vezes o número de bits de x . Alternativamente, o método de Horner pode ser calculado com n fundido multiplicação-adições . O método de Horner também pode ser estendido para avaliar as primeiras k derivadas do polinômio com acréscimos e multiplicações de kn .

O método de Horner é ótimo, no sentido de que qualquer algoritmo para avaliar um polinômio arbitrário deve usar pelo menos o mesmo número de operações. Alexander Ostrowski provou em 1954 que o número de acréscimos necessários é mínimo. Victor Pan provou em 1966 que o número de multiplicações é mínimo. No entanto, quando x é uma matriz, o método de Horner não é o ideal .

Isso pressupõe que o polinômio é avaliado na forma monomial e nenhum pré-condicionamento da representação é permitido, o que faz sentido se o polinômio for avaliado apenas uma vez. No entanto, se o pré-condicionamento for permitido e o polinômio for avaliado muitas vezes, algoritmos mais rápidos são possíveis . Eles envolvem uma transformação da representação do polinômio. Em geral, um polinômio grau n pode ser avaliado usando apenas ⌊ n / 2 ⌋ +2 multiplicações e n adições.

Avaliação paralela

Uma desvantagem da regra de Horner é que todas as operações são sequencialmente dependentes , portanto, não é possível tirar vantagem do paralelismo de nível de instrução em computadores modernos. Na maioria das aplicações onde a eficiência da avaliação polinomial é importante, muitos polinômios de baixa ordem são avaliados simultaneamente (para cada pixel ou polígono em computação gráfica, ou para cada quadrado de grade em uma simulação numérica), portanto, não é necessário encontrar paralelismo dentro de um avaliação de polinômio único.

Se, no entanto, alguém está avaliando um único polinômio de ordem muito alta, pode ser útil dividi-lo da seguinte forma:

${\ displaystyle {\ begin {alinhado} p (x) & = \ sum _ {i = 0} ^ {n} a_ {i} x ^ {i} \\ & = a_ {0} + a_ {1} x + a_ {2} x ^ {2} + a_ {3} x ^ {3} + \ cdots + a_ {n} x ^ {n} \\ & = \ left (a_ {0} + a_ {2} x ^ {2} + a_ {4} x ^ {4} + \ cdots \ right) + \ left (a_ {1} x + a_ {3} x ^ {3} + a_ {5} x ^ {5} + \ cdots \ right) \\ & = \ left (a_ {0} + a_ {2} x ^ {2} + a_ {4} x ^ {4} + \ cdots \ right) + x \ left (a_ {1 } + a_ {3} x ^ {2} + a_ {5} x ^ {4} + \ cdots \ direita) \\ & = \ sum _ {i = 0} ^ {\ lfloor n / 2 \ rfloor} a_ {2i} x ^ {2i} + x \ sum _ {i = 0} ^ {\ lfloor n / 2 \ rfloor} a_ {2i + 1} x ^ {2i} \\ & = p_ {0} (x ^ {2}) + xp_ {1} (x ^ {2}). \\\ end {alinhado}}}$

De forma mais geral, o somatório pode ser dividido em k partes:

${\ displaystyle {\ begin {alinhados} p (x) & = \ sum _ {i = 0} ^ {n} a_ {i} x ^ {i} \\ & = \ sum _ {j = 0} ^ { k-1} x ^ {j} \ sum _ {i = 0} ^ {\ lfloor n / k \ rfloor} a_ {ki + j} x ^ {ki} \\ & = \ sum _ {j = 0} ^ {k-1} x ^ {j} p_ {j} (x ^ {k}) \\\ fim {alinhado}}}$

onde as somas internas podem ser avaliadas usando instâncias paralelas separadas do método de Horner. Isso requer um pouco mais de operações do que o método básico de Horner, mas permite a execução de SIMD k -way da maioria delas. Os compiladores modernos geralmente avaliam os polinômios dessa maneira quando vantajosos, embora para cálculos de ponto flutuante isso exija a habilitação da matemática reassociativa (não segura).

Aplicação para multiplicação e divisão de ponto flutuante

O método de Horner é um método rápido e com código eficiente para multiplicação e divisão de números binários em um microcontrolador sem multiplicador de hardware . Um dos números binários a ser multiplicado é representado como um polinômio trivial, onde (usando a notação acima) , e . Então, x (ou x elevado a alguma potência) é repetidamente fatorado. Neste sistema numérico binário (base 2) , então potências de 2 são repetidamente fatoradas. ${\ displaystyle a_ {i} = 1}$${\ displaystyle x = 2}$${\ displaystyle x = 2}$

Exemplo

Por exemplo, para localizar o produto de dois números (0.15625) e m :

${\ displaystyle {\ begin {alinhados} (0,15625) m & = (0,00101_ {b}) m = (2 ^ {- 3} +2 ^ {- 5}) m = (2 ^ {- 3}) m + ( 2 ^ {- 5}) m \\ & = 2 ^ {- 3} (m + (2 ^ {- 2}) m) = 2 ^ {- 3} (m + 2 ^ {- 2} (m)) . \ end {alinhado}}}$

Método

Para encontrar o produto de dois números binários d e m :

1. Um registrador contendo o resultado intermediário é inicializado em d .

2. Comece com o bit diferente de zero menos significativo (mais à direita) em m .

2b. Conte (à esquerda) o número de posições de bit até o próximo bit diferente de zero mais significativo. Se não houver mais bits significativos, tome o valor da posição do bit atual.

2c. Usando esse valor, execute uma operação de deslocamento para a esquerda por esse número de bits no registro que contém o resultado intermediário

3. Se todos os bits diferentes de zero foram contados, o registrador de resultado intermediário agora contém o resultado final. Caso contrário, adicione d ao resultado intermediário e continue na etapa 2 com o próximo bit mais significativo em m .

Derivação

Em geral, para um número binário com valores de bit ( ), o produto é ${\ displaystyle d_ {3} d_ {2} d_ {1} d_ {0}}$

${\ displaystyle (d_ {3} 2 ^ {3} + d_ {2} 2 ^ {2} + d_ {1} 2 ^ {1} + d_ {0} 2 ^ {0}) m = d_ {3} 2 ^ {3} m + d_ {2} 2 ^ {2} m + d_ {1} 2 ^ {1} m + d_ {0} 2 ^ {0} m.}$

Nesta fase do algoritmo, é necessário que os termos com coeficientes de valor zero sejam descartados, de modo que apenas coeficientes binários iguais a um sejam contados, portanto, o problema de multiplicação ou divisão por zero não é um problema, apesar desta implicação no equação fatorada:

${\ displaystyle = d_ {0} \ left (m + 2 {\ frac {d_ {1}} {d_ {0}}} \ left (m + 2 {\ frac {d_ {2}} {d_ {1} }} \ left (m + 2 {\ frac {d_ {3}} {d_ {2}}} (m) \ right) \ right) \ right).}$

Todos os denominadores são iguais a um (ou o termo está ausente), então isso se reduz a

${\ displaystyle = d_ {0} (m + 2 {d_ {1}} (m + 2 {d_ {2}} (m + 2 {d_ {3}} (m)))),}$

ou de forma equivalente (conforme consistente com o "método" descrito acima)

${\ displaystyle = d_ {3} (m + 2 ^ {- 1} {d_ {2}} (m + 2 ^ {- 1} {d_ {1}} (m + {d_ {0}} (m)) )).}$

Em matemática binária (base 2), a multiplicação por uma potência de 2 é meramente uma operação de mudança de registro . Assim, a multiplicação por 2 é calculada na base 2 por um deslocamento aritmético . O fator (2 ⁻¹ ) é um deslocamento aritmético à direita , a (0) resulta em nenhuma operação (uma vez que 2 ⁰ = 1 é o elemento de identidade multiplicativo ) e a (2 ¹ ) resulta em um deslocamento aritmético à esquerda. O produto da multiplicação agora pode ser calculado rapidamente usando apenas operações de deslocamento aritmético, adição e subtração.

O método é particularmente rápido em processadores que suportam um deslocamento-e-adição-acumulação de instrução única. Comparado a uma biblioteca de ponto flutuante C, o método de Horner sacrifica alguma precisão, no entanto, é nominalmente 13 vezes mais rápido (16 vezes mais rápido quando o formulário de " dígito sinalizado canônico " (CSD) é usado) e usa apenas 20% do espaço de código.

Outras aplicações

Método de Horner pode ser usado para converter entre diferentes posicionais sistemas numerais - no caso em que x é a base do sistema de números, e as de _i coeficientes são os dígitos do base- x representação de um determinado número - e também pode ser usado se x é uma matriz , caso em que o ganho em eficiência computacional é ainda maior. No entanto, para tais casos, métodos mais rápidos são conhecidos.

Descoberta de raiz polinomial

Usando o algoritmo de divisão longa em combinação com o método de Newton , é possível aproximar as raízes reais de um polinômio. O algoritmo funciona da seguinte maneira. Dado um polinômio de grau com zeros, faça uma suposição inicial como essa . Agora repita as duas etapas a seguir: ${\ displaystyle p_ {n} (x)}$${\ displaystyle n}$${\ displaystyle z_ {n} <z_ {n-1} <\ cdots <z_ {1},}$${\ displaystyle x_ {0}}$${\ displaystyle z_ {1} <x_ {0}}$

1. Usando o método de Newton , encontrar o maior de zero de usar o palpite .${\ displaystyle z_ {1}}$${\ displaystyle p_ {n} (x)}$${\ displaystyle x_ {0}}$
2. Usando o método de Horner, divida para obter . Retorne à etapa 1, mas use o polinômio e a estimativa inicial .${\ displaystyle (x-z_ {1})}$${\ displaystyle p_ {n-1}}$${\ displaystyle p_ {n-1}}$${\ displaystyle z_ {1}}$

Essas duas etapas são repetidas até que todos os zeros reais sejam encontrados para o polinômio. Se os zeros aproximados não forem precisos o suficiente, os valores obtidos podem ser usados ​​como estimativas iniciais para o método de Newton, mas usando o polinômio completo em vez dos polinômios reduzidos.

Exemplo

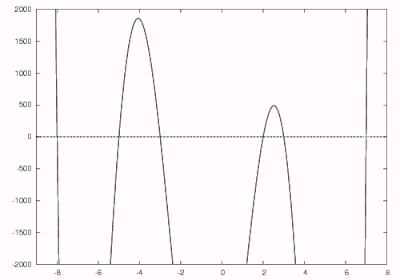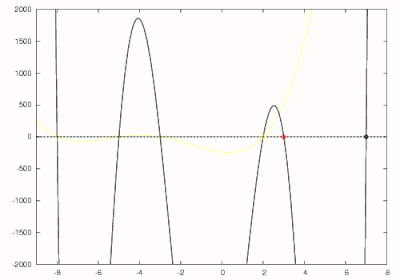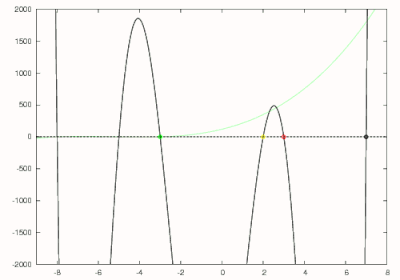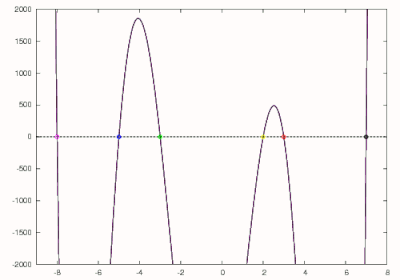
Considere o polinômio

${\ displaystyle p_ {6} (x) = (x + 8) (x + 5) (x + 3) (x-2) (x-3) (x-7)}$

que pode ser expandido para

${\ displaystyle p_ {6} (x) = x ^ {6} + 4x ^ {5} -72x ^ {4} -214x ^ {3} + 1127x ^ {2} + 1602x-5040.}$

Do exposto, sabemos que a maior raiz desse polinômio é 7, então podemos fazer uma estimativa inicial de 8. Usando o método de Newton, o primeiro zero de 7 é encontrado como mostrado em preto na figura à direita. O próximo é dividido por para obter ${\ displaystyle p (x)}$${\ displaystyle (x-7)}$

${\ displaystyle p_ {5} (x) = x ^ {5} + 11x ^ {4} + 5x ^ {3} -179x ^ {2} -126x + 720}$

que é desenhada em vermelho na figura à direita. O método de Newton é usado para encontrar o maior zero desse polinômio com uma estimativa inicial de 7. O maior zero desse polinômio que corresponde ao segundo maior zero do polinômio original é encontrado em 3 e é circulado em vermelho. O polinômio de grau 5 agora é dividido por para obter ${\ displaystyle (x-3)}$

${\ displaystyle p_ {4} (x) = x ^ {4} + 14x ^ {3} + 47x ^ {2} -38x-240}$

que é mostrado em amarelo. O zero para este polinômio é encontrado em 2 novamente usando o método de Newton e é circulado em amarelo. O método de Horner agora é usado para obter

${\ displaystyle p_ {3} (x) = x ^ {3} + 16x ^ {2} + 79x + 120}$

que é mostrado em verde e encontrado para ter um zero em -3. Este polinômio é ainda mais reduzido a

${\ displaystyle p_ {2} (x) = x ^ {2} + 13x + 40}$

que é mostrado em azul e resulta em zero de −5. A raiz final do polinômio original pode ser encontrada usando o zero final como uma estimativa inicial para o método de Newton ou reduzindo e resolvendo a equação linear. Como pode ser visto, as raízes esperadas de −8, −5, −3, 2, 3 e 7 foram encontradas. ${\ displaystyle p_ {2} (x)}$

Diferença dividida de um polinômio

O método de Horner pode ser modificado para calcular a diferença dividida Dado o polinômio (como antes) ${\ displaystyle (p (y) -p (x)) / (yx).}$

${\ displaystyle p (x) = \ sum _ {i = 0} ^ {n} a_ {i} x ^ {i} = a_ {0} + a_ {1} x + a_ {2} x ^ {2} + a_ {3} x ^ {3} + \ cdots + a_ {n} x ^ {n},}$

proceda da seguinte forma

${\ displaystyle {\ begin {alinhados} b_ {n} & = a_ {n}, & \ quad d_ {n} & = b_ {n}, \\ b_ {n-1} & = a_ {n-1} + b_ {n} x, & \ quad d_ {n-1} & = b_ {n-1} + d_ {n} y, \\ & {} \ \ \ vdots & \ quad & {} \ \ \ vdots \\ b_ {1} & = a_ {1} + b_ {2} x, & \ quad d_ {1} & = b_ {1} + d_ {2} y, \\ b_ {0} & = a_ {0 } + b_ {1} x. \ end {alinhado}}}$

Na conclusão, temos

${\ displaystyle {\ begin {alinhados} p (x) & = b_ {0}, \\ {\ frac {p (y) -p (x)} {yx}} & = d_ {1}, \\ p (y) & = b_ {0} + (yx) d_ {1}. \ end {alinhado}}}$

Este cálculo da diferença dividida está sujeito a menos erros de arredondamento do que a avaliação e separadamente, especialmente quando . Substituir neste método dá , a derivada de . ${\ displaystyle p (x)}$${\ displaystyle p (y)}$${\ displaystyle x \ approx y}$${\ displaystyle y = x}$${\ displaystyle d_ {1} = p '(x)}$${\ displaystyle p (x)}$

História

O artigo de Horner, intitulado "Um novo método de resolver equações numéricas de todas as ordens, por aproximação contínua", foi lido perante a Royal Society of London, em sua reunião em 1 de julho de 1819, com uma sequência em 1823. Artigo de Horner na Parte II of Philosophical Transactions of the Royal Society of London para 1819 foi calorosamente e amplamente recebido por um revisor na edição de The Monthly Review: ou, Literary Journal de abril de 1820; em comparação, um artigo técnico de Charles Babbage é descartado secamente nesta revisão. A sequência de revisões em The Monthly Review de setembro de 1821 conclui que Holdred foi a primeira pessoa a descobrir uma solução prática direta e geral de equações numéricas. Fuller mostrou que o método no artigo de Horner de 1819 difere do que posteriormente ficou conhecido como "método de Horner" e que, em conseqüência, a prioridade desse método deveria ir para Holdred (1820).

Ao contrário de seus contemporâneos ingleses, Horner baseou-se na literatura continental, notadamente na obra de Arbogast . Horner também é conhecido por ter feito uma leitura atenta do livro de John Bonneycastle sobre álgebra, embora tenha negligenciado a obra de Paolo Ruffini .

Embora Horner seja creditado por tornar o método acessível e prático, ele já era conhecido muito antes de Horner. Em ordem cronológica inversa, o método de Horner já era conhecido por:

• Paolo Ruffini em 1809 (ver regra de Ruffini )
• Isaac Newton em 1669
• o matemático chinês Zhu Shijie no século 14
• o matemático chinês Qin Jiushao em seu Tratado de Matemática em Nove Seções no século 13
• o matemático persa Sharaf al-Dīn al-Ṭūsī no século 12 (o primeiro a usar esse método em um caso geral de equação cúbica)
• o matemático chinês Jia Xian no século 11 ( dinastia Song )
• Os nove capítulos sobre a arte matemática , uma obra chinesa da dinastia Han (202 aC - 220 dC) editada por Liu Hui (fl. Século III).

Qin Jiushao , em seu Shu Shu Jiu Zhang ( Tratado de Matemática em Nove Seções ; 1247), apresenta um portfólio de métodos do tipo Horner para resolver equações polinomiais, que foi baseado em trabalhos anteriores do matemático Jia Xian da dinastia Song do século XI ; por exemplo, um método é especificamente adequado para bi-quintics, do qual Qin dá um exemplo, de acordo com o costume chinês de estudos de caso. Yoshio Mikami em Desenvolvimento da Matemática na China e no Japão (Leipzig 1913) escreveu:

"... quem pode negar o fato de o processo ilustre de Horner ter sido usado na China pelo menos quase seis longos séculos antes do que na Europa ... É claro que não pretendemos de forma alguma atribuir a invenção de Horner a uma origem chinesa, mas o lapso de tempo torna não de todo impossível que os europeus pudessem conhecer o método chinês de forma direta ou indireta. "

Ulrich Libbrecht concluiu: É óbvio que este procedimento é uma invenção chinesa ... o método não era conhecido na Índia . Ele disse, Fibonacci provavelmente aprendeu com os árabes, que talvez tenham emprestado dos chineses. A extração de raízes quadradas e cúbicas ao longo de linhas semelhantes já foi discutida por Liu Hui em conexão com os Problemas IV.16 e 22 em Jiu Zhang Suan Shu , enquanto Wang Xiaotong no século 7 supõe que seus leitores podem resolver cúbicas por um método de aproximação descrito em seu livro Jigu Suanjing .

Veja também

• Algoritmo de Clenshaw para avaliar polinômios na forma de Chebyshev
• Algoritmo de Boor para avaliar ranhuras em B-spline forma
• Algoritmo de De Casteljau para avaliar polinômios na forma de Bézier
• Esquema de Estrin para facilitar a paralelização em arquiteturas de computador modernas
• O método de Lill para aproximar as raízes graficamente
• Regra de Ruffini e divisão sintética para dividir um polinômio por um binômio da forma x - r

Notas

Referências

• Berggren, JL (1990). "Inovação e tradição no Muadalat de Sharaf al-Din al-Tusi". Jornal da Sociedade Oriental Americana . 110 (2): 304–309. doi : 10.2307 / 604533 . JSTOR  604533 .
• Cajori, Florian (1911). "Método de aproximação de Horner antecipado por Ruffini" . Boletim da American Mathematical Society . 17 (8): 409–414. doi : 10.1090 / s0002-9904-1911-02072-9 . Leia antes da Seção Sudoeste da American Mathematical Society em 26 de novembro de 1910.
• Cormen, Thomas H .; Leiserson, Charles E .; Rivest, Ronald L .; Stein10.1016 / 0315-0860 (81) 90069-0, Clifford (2009). "Introdução aos Algoritmos" . Historia Mathematica (3ª ed.). MIT Press. 8 (3): 277–318. doi : 10.1016 / 0315-0860 (81) 90069-0 .
• Fateman, RJ ; Kahan, W. (2000). Melhorar integrais exatas de sistemas de álgebra simbólica (PDF) (Relatório). PAM. University of California, Berkeley: Center for Pure and Applied Mathematics. Arquivado do original (PDF) em 14/08/2017 . Página visitada em 2017-05-17 .
• Fuller, AT (1999). "Horner versus Holdred: um episódio na história da computação raiz" . Historia Mathematica . 26 : 29–51. doi : 10.1006 / hmat.1998.2214 .
• Higham, Nicholas (2002). Precisão e estabilidade de algoritmos numéricos . SIAM. ISBN 978-0-89871-521-7.
• Holdred, T. (1820). Um novo método de resolver equações com facilidade e rapidez. pelo qual o valor verdadeiro da quantidade desconhecida é encontrado sem redução anterior. Com um suplemento, contendo dois outros métodos de resolução de equações, derivados do mesmo princípio (PDF) . Richard Watts. Arquivado do original (PDF) em 06/01/2014 . Página visitada em 2012-12-10 .

  O método de Holdred está no suplemento seguinte à página de número 45 (que é a 52ª página da versão em pdf).

• Horner, William George (julho de 1819). "Um novo método de resolução de equações numéricas de todas as ordens, por aproximação contínua" (PDF) . Transações filosóficas . Royal Society of London. 109 : 308–335. doi : 10.1098 / rstl.1819.0023 . JSTOR  107508 . S2CID  186210512 . Arquivado do original (PDF) em 28-03-2017 . Recuperado em 28-03-2017 .

  Disponível diretamente online através do link, mas também reimpresso com avaliação em DE Smith: A Source Book in Mathematics , McGraw-Hill, 1929; Reimpressão de Dover, 2 vols, 1959.

• Knuth, Donald (1997). The Art of Computer Programming . Vol. 2: Seminumerical Algorithms (3rd ed.). Addison-Wesley. pp. 486-488 na seção 4.6.4. ISBN 978-0-201-89684-8. |volume=tem texto extra ( ajuda )
• Kress, Rainer (1991). Análise Numérica . Springer.
• Kripasagar, Venkat (março de 2008). "Micro Matemática Eficiente - Técnicas de Multiplicação e Divisão para MCUs". Revista Circuit Cellar (212).
• Libbrecht, Ulrich (2005). "Capítulo 13" . Matemática chinesa no século XIII (2ª ed.). Dover. ISBN 978-0-486-44619-6. Arquivado do original em 06/06/2016 . Página visitada em 2016-08-23 .
• Mikami, Yoshio (1913). "Capítulo 11. Ch'in Chiu-Shao" . O Desenvolvimento da Matemática na China e no Japão (1ª ed.). Reimpressão da Chelsea Publishing Co. pp. 74–77.
• Ostrowski, Alexander M. (1954). "Sobre dois problemas de álgebra abstrata ligados à regra de Horner" . Estudos em Matemática e Mecânica apresentados a Richard von Mises . Academic Press. pp. 40–48. ISBN 978-1-4832-3272-0.
• Pan, Y. Ja (1966). "Sobre meios de cálculo de valores de polinômios". Matemática russa. Pesquisas . 21 : 105–136. doi : 10.1070 / rm1966v021n01abeh004147 .
• Pankiewicz, W. (1968). "Algoritmo 337: cálculo de um polinômio e seus valores derivados pelo esquema de Horner". Comunicações da ACM . ACM. 11 (9): 633. doi : 10.1145 / 364063.364089 . S2CID  52859619 .
• Spiegel, Murray R. (1956). Esboço de Teoria e Problemas de Álgebra Universitária de Schaum . McGraw-Hill.
• Temple, Robert (1986). O gênio da China: 3.000 anos de ciência, descoberta e invenção . Simon e Schuster. ISBN 978-0-671-62028-8.
• Whittaker, ET ; Robinson, G. (1924). O cálculo das observações . Londres: Blackie.
• Wylie, Alexander (1897). "Jottings on the Science of Chinese Arithmetic" . Pesquisas chinesas . Xangai. pp. 159–194.

  Reproduzido de edições do The North China Herald (1852).

links externos

• "Esquema de Horner" , Encyclopedia of Mathematics , EMS Press , 2001 [1994]
• Qiu Jin-Shao, Shu Shu Jiu Zhang (Cong Shu Ji Cheng ed.)
• Para obter mais informações sobre o aplicativo de localização de raiz, consulte [1]