Ponto Misiurewicz - Misiurewicz point

Em matemática, um ponto de Misiurewicz é um parâmetro no conjunto de Mandelbrot (o espaço de parâmetros de polinômios quadráticos) para o qual o ponto crítico é estritamente pré-periódico (ou seja, torna-se periódico após finitas iterações, mas não é periódico em si). Por analogia, o termo ponto de Misiurewicz também é usado para parâmetros em um conjunto multibrot onde o ponto crítico único é estritamente pré-periódico. (Este termo faz menos sentido para mapas em maior generalidade que têm mais de um ponto crítico (livre) porque alguns pontos críticos podem ser periódicos e outros não.)

Ponto principal Misiurewicz da esteira 31/01

Notação matemática

Um parâmetro é um ponto Misiurewicz se satisfizer as equações ${\ displaystyle c}$ ${\ displaystyle M_ {k, n}}$

{\ displaystyle f_ {c} ^ {(k)} (z_ {cr}) = f_ {c} ^ {(k + n)} (z_ {cr})}

e

{\ displaystyle f_ {c} ^ {(k-1)} (z_ {cr}) \ neq f_ {c} ^ {(k + n-1)} (z_ {cr})}

tão :

{\ displaystyle M_ {k, n} = c: f_ {c} ^ {(k)} (z_ {cr}) = f_ {c} ^ {(k + n)} (z_ {cr})}

Onde :

${\ displaystyle z_ {cr}}$ é um ponto crítico de , ${\ displaystyle f_ {c}}$
${\ displaystyle k}$ e são inteiros positivos, ${\ displaystyle n}$
${\ displaystyle f_ {c} ^ {(k)}}$ denota a -ésima iteração de . ${\ displaystyle k}$ ${\ displaystyle f_ {c}}$

Nome

Os pontos Misiurewicz foram nomeados em homenagem ao matemático polonês-americano Michał Misiurewicz .

O termo "ponto Misiurewicz" é usado de forma ambígua: Misiurewicz originalmente investigou mapas nos quais todos os pontos críticos eram não recorrentes (ou seja, há uma vizinhança de cada ponto crítico que não é visitado pela órbita desse ponto crítico), e este o significado é firmemente estabelecido no contexto da dinâmica dos mapas de intervalo iterativos. O caso de que, para um polinômio quadrático, o ponto crítico único é estritamente pré-periódico é apenas um caso muito especial. Nesse sentido restrito, o termo é usado em dinâmicas complexas; um mais apropriado seria os pontos Misiurewicz – Thurston (após William Thurston , que investigou mapas racionais pós-criticamente finitos).

Mapas quadráticos

Um polinômio quadrático complexo possui apenas um ponto crítico. Por uma conjugação adequada, qualquer polinômio quadrático pode ser transformado em um mapa da forma que tem um único ponto crítico em . Os pontos Misiurewicz desta família de mapas são raízes das equações ${\ displaystyle P_ {c} (z) = z ^ {2} + c}$ ${\ displaystyle z = 0}$

{\ displaystyle P_ {c} ^ {(k)} (0) = P_ {c} ^ {(k + n)} (0)}

,

(sujeito à condição de que o ponto crítico não seja periódico), onde:

k é o pré-período
n é o período
${\ displaystyle P_ {c} ^ {(n)} = P_ {c} (P_ {c} ^ {(n-1)})}$ denota a composição n- dobrada de consigo mesmo, isto é, a n- ^ésimaiteração de . ${\ displaystyle P_ {c} (z) = z ^ {2} + c}$ ${\ displaystyle P_ {c}}$

Por exemplo, os pontos Misiurewicz com k = 2 e n = 1, denotados por H _2,1 , são raízes de

{\ displaystyle P_ {c} ^ {(2)} (0) = P_ {c} ^ {(3)} (0)}

{\ displaystyle \ Rightarrow c ^ {2} + c = (c ^ {2} + c) ^ {2} + c}

{\ displaystyle \ Rightarrow c ^ {4} + 2c ^ {3} = 0}

.

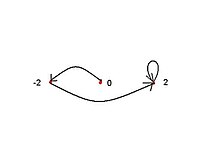
A raiz c = 0 não é um ponto Misiurewicz porque o ponto crítico é um ponto fixo quando c = 0 e, portanto, é periódico em vez de pré-periódico. Isso deixa um único ponto Misiurewicz M _2,1 em c = −2.

Propriedades dos pontos Misiurewicz de mapeamento quadrático complexo

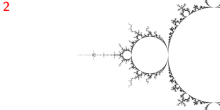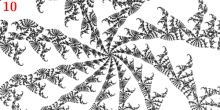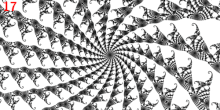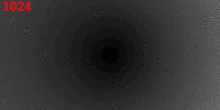
Os pontos Misiurewicz pertencem ao limite do conjunto de Mandelbrot . Os pontos Misiurewicz são densos na fronteira do conjunto Mandelbrot.

Se for um ponto Misiurewicz, o conjunto Julia preenchido associado é igual ao conjunto Julia e significa que o conjunto Julia preenchido não tem interior . ${\ displaystyle c}$

Se for um ponto Misiurewicz, então no conjunto Julia correspondente todos os ciclos periódicos são repelentes (em particular o ciclo em que a órbita crítica cai). ${\ displaystyle c}$

O conjunto Mandelbrot e o conjunto Julia são localmente assintoticamente auto-semelhantes em torno dos pontos Misiurewicz. ${\ displaystyle J_ {c}}$

Tipos

Os pontos Misiurewicz podem ser classificados de acordo com o número de raios externos que pousam sobre eles, ou seja, pontos onde os ramos se encontram:

pontos de ramificação, que desconectam o conjunto de Mandelbrot, com 3 ou mais argumentos externos (ou ângulos) ;
pontos não ramificados, com exatamente 2 argumentos externos (pontos de arcos dentro do conjunto de Mandelbrot) que são menos conspícuos e não são facilmente encontrados em imagens; e
pontos finais, com 1 argumento externo (dicas de ramificação).

De acordo com o Teorema da Ramificação do conjunto de Mandelbrot, todos os pontos de ramificação do conjunto de Mandelbrot são pontos de Misiurewicz. Além disso, em um sentido combinatório, os componentes hiperbólicos são representados por seus centros.

A maioria dos parâmetros Misiurewicz no conjunto de Mandelbrot parecem "centros de espirais". A explicação para isso é que em um parâmetro Misiurewicz, o valor crítico salta para um ciclo periódico de repulsão após um número finito de iterações. Em cada ponto durante o ciclo, o conjunto Julia é assintoticamente auto-similar por uma multiplicação complexa pela derivada desse ciclo. Se a derivada não for real, isso implica que o conjunto Julia próximo ao ciclo periódico tem uma estrutura em espiral. Assim, uma estrutura espiral semelhante ocorre no conjunto de Julia próximo ao valor crítico e, pelo teorema de Tan Lei , também no conjunto de Mandelbrot próximo a qualquer parâmetro de Misiurewicz para o qual a órbita de repulsão tem um multiplicador não real. Dependendo do valor deste multiplicador, a forma da espiral pode parecer mais ou menos pronunciada. O número de braços na espiral é igual ao número de ramos no parâmetro Misiurewicz, e isso é igual ao número de ramos no valor crítico no conjunto Julia. Mesmo o ponto principal de Misiurewicz no ramo 1/3, no final dos raios de parâmetro nos ângulos 9/56, 11/56 e 15/56, acaba sendo assintoticamente uma espiral, com infinitas voltas, embora isso é difícil de ver sem ampliação.

Argumentos externos

Os argumentos externos dos pontos Misiurewicz, medidos em turnos são:

números racionais
fração adequada com denominador par
- frações diádicas com denominador e expansão finita ( terminação ), como: ${\ displaystyle = 2 ^ {b}}$
${\ displaystyle {\ frac {1} {2}} _ {10} = 0,5_ {10} = 0,1_ {2}}$
- fração com denominador e expansão repetida como: ${\ displaystyle = a * 2 ^ {b}}$
${\ displaystyle {\ frac {1} {6}} _ {10} = {\ frac {1} {2 * 3}} _ {10} = 0,16666 ..._ {10} = 0,0 (01) ..._ {2}}$ .

onde: aeb são inteiros positivos eb é ímpar, o número subscrito mostra a base do sistema numeral .

Exemplos de pontos Misiurewicz de mapeamento quadrático complexo

Pontos finais

Órbita do ponto crítico sob

{\ displaystyle z = 0}

{\ displaystyle f _ {- 2}}

{\ displaystyle c = M_ {2,1}}

Ponto : ${\ displaystyle c = M_ {2,2} = i}$

é uma ponta do filamento
Suas órbitas críticas são ${\ displaystyle \ {0, i, i-1, -i, i-1, -i ... \}}$
ponto de aterrissagem do raio externo para o ângulo = 1/6

Apontar ${\ displaystyle c = M_ {2,1} = - 2}$

é o ponto final da antena principal do conjunto Mandelbrot
Suas órbitas críticas são ${\ displaystyle \ {0, -2,2,2,2, ... \}}$
Sequência simbólica = CLRRR ...
pré-período é 2 e período 1

Observe que é o plano z (plano dinâmico ), não o plano c ( plano de parâmetros ) e o ponto não é o mesmo ponto que . ${\ displaystyle z = -2}$ ${\ displaystyle c = -2}$

O ponto é o ponto de aterrissagem de apenas um raio externo (raio de parâmetro) de ângulo 1/2. ${\ displaystyle c = -2 = M_ {2,1}}$

Pontos não ramificados

{\ displaystyle c = M_ {23,2}}

Point fica perto de um ponto Misiurewicz . Isto é ${\ displaystyle c = -0,77568377 + 0,13646737 * i}$ ${\ displaystyle M_ {23,2}}$

um centro de uma espiral de dois braços
um ponto de aterrissagem de 2 raios externos com ângulos: e onde o denominador é ${\ displaystyle {\ frac {8388611} {25165824}}}$ ${\ displaystyle {\ frac {8388613} {25165824}}}$ ${\ displaystyle 3 * 2 ^ {23}}$
ponto pré -período com pré -período e período ${\ displaystyle k = 23}$ ${\ displaystyle n = 2}$

Point fica perto de um ponto Misiurewicz , ${\ displaystyle c = -1.54368901269109}$ ${\ displaystyle M_ {3,1}}$

que é ponto de aterragem para o par de raios: , ${\ displaystyle {\ frac {5} {12}}}$ ${\ displaystyle {\ frac {7} {12}}}$
tem pré -período e período ${\ displaystyle k = 3}$ ${\ displaystyle n = 1}$