Provas de identidades trigonométricas - Proofs of trigonometric identities

As principais identidades trigonométricas entre funções trigonométricas são provadas , usando principalmente a geometria do triângulo retângulo . Para ângulos maiores e negativos , consulte Funções trigonométricas .

Identidades trigonométricas elementares

Definições

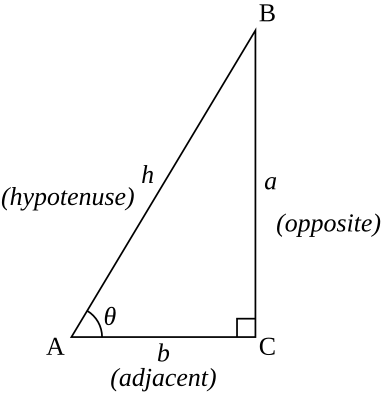
As funções trigonométricas especificam as relações entre os comprimentos laterais e os ângulos internos de um triângulo retângulo. Por exemplo, o seno do ângulo θ é definido como sendo o comprimento do lado oposto dividido pelo comprimento da hipotenusa.

As seis funções trigonométricas são definidas para cada número real , exceto, para alguns deles, para ângulos que diferem de 0 por um múltiplo do ângulo reto (90 °). Referindo-se ao diagrama à direita, as seis funções trigonométricas de θ são, para ângulos menores do que o ângulo reto:

${\ displaystyle \ sin \ theta = {\ frac {\ mathrm {oposto}} {\ mathrm {hipotenusa}}} = {\ frac {a} {h}}}$

${\ displaystyle \ cos \ theta = {\ frac {\ mathrm {adjacente}} {\ mathrm {hipotenusa}}} = {\ frac {b} {h}}}$

${\ displaystyle \ tan \ theta = {\ frac {\ mathrm {oposto}} {\ mathrm {adjacente}}} = {\ frac {a} {b}}}$

${\ displaystyle \ cot \ theta = {\ frac {\ mathrm {adjacente}} {\ mathrm {oposto}}} = {\ frac {b} {a}}}$

${\ displaystyle \ sec \ theta = {\ frac {\ mathrm {hipotenusa}} {\ mathrm {adjacente}}} = {\ frac {h} {b}}}$

${\ displaystyle \ csc \ theta = {\ frac {\ mathrm {hipotenusa}} {\ mathrm {oposto}}} = {\ frac {h} {a}}}$

Razão de identidades

No caso de ângulos menores do que um ângulo reto, as seguintes identidades são consequências diretas das definições acima por meio da divisão de identidade

${\ displaystyle {\ frac {a} {b}} = {\ frac {\ left ({\ frac {a} {h}} \ right)} {\ left ({\ frac {b} {h}} \ direito)}}.}$

Eles permanecem válidos para ângulos maiores que 90 ° e para ângulos negativos.

${\ displaystyle \ tan \ theta = {\ frac {\ mathrm {oposto}} {\ mathrm {adjacente}}} = {\ frac {\ left ({\ frac {\ mathrm {oposto}} {\ mathrm {hipotenusa} }} \ right)} {\ left ({\ frac {\ mathrm {adjacente}} {\ mathrm {hipotenusa}}} \ right)}} = {\ frac {\ sin \ theta} {\ cos \ theta}} }$

${\ displaystyle \ cot \ theta = {\ frac {\ mathrm {adjacente}} {\ mathrm {oposto}}} = {\ frac {\ left ({\ frac {\ mathrm {adjacente}} {\ mathrm {adjacente} }} \ right)} {\ left ({\ frac {\ mathrm {oposto}} {\ mathrm {adjacente}}} \ right)}} = {\ frac {1} {\ tan \ theta}} = {\ frac {\ cos \ theta} {\ sin \ theta}}}$

${\ displaystyle \ sec \ theta = {\ frac {1} {\ cos \ theta}} = {\ frac {\ mathrm {hipotenusa}} {\ mathrm {adjacente}}}}$

${\ displaystyle \ csc \ theta = {\ frac {1} {\ sin \ theta}} = {\ frac {\ mathrm {hipotenusa}} {\ mathrm {oposto}}}}$

${\ displaystyle \ tan \ theta = {\ frac {\ mathrm {oposto}} {\ mathrm {adjacente}}} = {\ frac {\ left ({\ frac {\ mathrm {oposto} \ times \ mathrm {hipotenusa} } {\ mathrm {oposto} \ times \ mathrm {adjacente}}} \ direita)} {\ left ({\ frac {\ mathrm {adjacente} \ times \ mathrm {hipotenusa}} {\ mathrm {oposto} \ times \ mathrm {adjacente}}} \ direita)}} = {\ frac {\ esquerda ({\ frac {\ mathrm {hipotenusa}} {\ mathrm {adjacente}}} \ direita)} {\ esquerda ({\ frac {\ mathrm {hipotenusa}} {\ mathrm {oposto}}} \ direita)}} = {\ frac {\ sec \ theta} {\ csc \ theta}}}$

Ou

${\ displaystyle \ tan \ theta = {\ frac {\ sin \ theta} {\ cos \ theta}} = {\ frac {\ left ({\ frac {1} {\ csc \ theta}} \ right)} { \ left ({\ frac {1} {\ sec \ theta}} \ right)}} = {\ frac {\ left ({\ frac {\ csc \ theta \ sec \ theta} {\ csc \ theta}} \ direita)} {\ left ({\ frac {\ csc \ theta \ sec \ theta} {\ sec \ theta}} \ right)}} = {\ frac {\ sec \ theta} {\ csc \ theta}}}$

${\ displaystyle \ cot \ theta = {\ frac {\ csc \ theta} {\ sec \ theta}}}$

Identidades de ângulo complementar

Dois ângulos cuja soma é π / 2 radianos (90 graus) são complementares . No diagrama, os ângulos nos vértices A e B são complementares, então podemos trocar a e b, e mudar θ para π / 2 - θ, obtendo:

${\ displaystyle \ sin \ left (\ pi / 2- \ theta \ right) = \ cos \ theta}$

${\ displaystyle \ cos \ left (\ pi / 2- \ theta \ right) = \ sin \ theta}$

${\ displaystyle \ tan \ left (\ pi / 2- \ theta \ right) = \ cot \ theta}$

${\ displaystyle \ cot \ left (\ pi / 2- \ theta \ right) = \ tan \ theta}$

${\ displaystyle \ sec \ left (\ pi / 2- \ theta \ right) = \ csc \ theta}$

${\ displaystyle \ csc \ left (\ pi / 2- \ theta \ right) = \ sec \ theta}$

Identidades pitagóricas

Identidade 1:

${\ displaystyle \ sin ^ {2} (x) + \ cos ^ {2} (x) = 1}$

Os dois resultados a seguir seguem disso e das identidades de razão. Para obter o primeiro, divida os dois lados de por ; para o segundo, divida por . ${\ displaystyle \ sin ^ {2} (x) + \ cos ^ {2} (x) = 1}$${\ displaystyle \ cos ^ {2} (x)}$${\ displaystyle \ sin ^ {2} (x)}$

${\ displaystyle \ tan ^ {2} (x) +1 \ = \ sec ^ {2} (x)}$

${\ displaystyle 1 \ + \ cot ^ {2} (x) = \ csc ^ {2} (x)}$

de forma similar

${\ displaystyle 1 \ + \ cot ^ {2} (x) = \ csc ^ {2} (x)}$

${\ displaystyle \ csc ^ {2} (x) - \ cot ^ {2} (x) = 1}$

Identidade 2:

O seguinte explica todas as três funções recíprocas.

${\ displaystyle \ csc ^ {2} (x) + \ sec ^ {2} (x) - \ cot ^ {2} (x) = 2 \ + \ tan ^ {2} (x)}$

Prova 2:

Consulte o diagrama do triângulo acima. Observe isso pelo teorema de Pitágoras . ${\ displaystyle a ^ {2} + b ^ {2} = h ^ {2}}$

${\ displaystyle \ csc ^ {2} (x) + \ sec ^ {2} (x) = {\ frac {h ^ {2}} {a ^ {2}}} + {\ frac {h ^ {2 }} {b ^ {2}}} = {\ frac {a ^ {2} + b ^ {2}} {a ^ {2}}} + {\ frac {a ^ {2} + b ^ {2 }} {b ^ {2}}} = 2 \ + {\ frac {b ^ {2}} {a ^ {2}}} + {\ frac {a ^ {2}} {b ^ {2}} }}$

Substituindo por funções apropriadas -

${\ displaystyle 2 \ + {\ frac {b ^ {2}} {a ^ {2}}} + {\ frac {a ^ {2}} {b ^ {2}}} = 2 \ + \ tan ^ {2} (x) + \ cot ^ {2} (x)}$

A reorganização dá:

${\ displaystyle \ csc ^ {2} (x) + \ sec ^ {2} (x) - \ cot ^ {2} (x) = 2 \ + \ tan ^ {2} (x)}$

Identidades de soma angular

Seno

Ilustração da fórmula da soma.

Desenhe uma linha horizontal (o eixo x ); marque uma origem O. Desenhe uma linha de O em um ângulo acima da linha horizontal e uma segunda linha em um ângulo acima dela ; o ângulo entre a segunda linha e o eixo x é . ${\ displaystyle \ alpha}$${\ displaystyle \ beta}$${\ displaystyle \ alpha + \ beta}$

Coloque P na linha definida por a uma unidade de distância da origem. ${\ displaystyle \ alpha + \ beta}$

Seja PQ uma linha perpendicular à linha OQ definida pelo ângulo , desenhada do ponto Q nesta linha até o ponto P. OQP é um ângulo reto. ${\ displaystyle \ alpha}$${\ displaystyle \ portanto}$

Seja QA uma perpendicular do ponto A no eixo x a Q e PB uma perpendicular do ponto B no eixo x a P. OAQ e OBP são ângulos retos. ${\ displaystyle \ portanto}$

Desenhe R em PB para que QR seja paralelo ao eixo x .

Agora ângulo (porque , fazendo e finalmente ) ${\ displaystyle RPQ = \ alpha}$${\ displaystyle OQA = {\ frac {\ pi} {2}} - \ alpha}$${\ displaystyle RQO = \ alpha, RQP = {\ frac {\ pi} {2}} - \ alpha}$${\ displaystyle RPQ = \ alpha}$

${\ displaystyle RPQ = {\ tfrac {\ pi} {2}} - RQP = {\ tfrac {\ pi} {2}} - ({\ tfrac {\ pi} {2}} - RQO) = RQO = \ alfa}$

${\ displaystyle OP = 1}$

${\ displaystyle PQ = \ sin \ beta}$

${\ displaystyle OQ = \ cos \ beta}$

${\ displaystyle {\ frac {AQ} {OQ}} = \ sin \ alpha}$, tão ${\ displaystyle AQ = \ sin \ alpha \ cos \ beta}$

${\ displaystyle {\ frac {PR} {PQ}} = \ cos \ alpha}$, tão ${\ displaystyle PR = \ cos \ alpha \ sin \ beta}$

${\ displaystyle \ sin (\ alpha + \ beta) = PB = RB + PR = AQ + PR = \ sin \ alpha \ cos \ beta + \ cos \ alpha \ sin \ beta}$

Substituindo por e usando Simetria , também temos: ${\ displaystyle - \ beta}$${\ displaystyle \ beta}$

${\ displaystyle \ sin (\ alpha - \ beta) = \ sin \ alpha \ cos (- \ beta) + \ cos \ alpha \ sin (- \ beta)}$

${\ displaystyle \ sin (\ alpha - \ beta) = \ sin \ alpha \ cos \ beta - \ cos \ alpha \ sin \ beta}$

Outra prova rigorosa, e muito mais fácil, pode ser dada usando a fórmula de Euler , conhecida por análises complexas. A fórmula de Euler é:

${\ displaystyle e ^ {i \ varphi} = \ cos \ varphi + i \ sin \ varphi}$

Segue-se que para ângulos e temos: ${\ displaystyle \ alpha}$${\ displaystyle \ beta}$

${\ displaystyle e ^ {i (\ alpha + \ beta)} = \ cos (\ alpha + \ beta) + i \ sin (\ alpha + \ beta)}$

Também usando as seguintes propriedades de funções exponenciais:

${\ displaystyle e ^ {i (\ alpha + \ beta)} = e ^ {i \ alpha} e ^ {i \ beta} = (\ cos \ alpha + i \ sin \ alpha) (\ cos \ beta + i \ sin \ beta)}$

Avaliando o produto:

${\ displaystyle e ^ {i (\ alpha + \ beta)} = (\ cos \ alpha \ cos \ beta - \ sin \ alpha \ sin \ beta) + i (\ sin \ alpha \ cos \ beta + \ sin \ beta \ cos \ alpha)}$

Equacionando partes reais e imaginárias:

${\ displaystyle \ cos (\ alpha + \ beta) = \ cos \ alpha \ cos \ beta - \ sin \ alpha \ sin \ beta}$

${\ displaystyle \ sin (\ alpha + \ beta) = \ sin \ alpha \ cos \ beta + \ sin \ beta \ cos \ alpha}$

Mas este é um tipo de argumento circular , uma vez que a prova da fórmula de Euler requer saber que a derivada de seno é cosseno, o que só pode ser provado usando a identidade para o seno da soma de dois ângulos.

Cosine

Usando a figura acima,

${\ displaystyle OP = 1}$

${\ displaystyle PQ = \ sin \ beta}$

${\ displaystyle OQ = \ cos \ beta}$

${\ displaystyle {\ frac {OA} {OQ}} = \ cos \ alpha}$, tão ${\ displaystyle OA = \ cos \ alpha \ cos \ beta}$

${\ displaystyle {\ frac {RQ} {PQ}} = \ sin \ alpha}$, tão ${\ displaystyle RQ = \ sin \ alpha \ sin \ beta}$

${\ displaystyle \ cos (\ alpha + \ beta) = OB = OA-BA = OA-RQ = \ cos \ alpha \ cos \ beta \ - \ sin \ alpha \ sin \ beta}$

Substituindo por e usando Simetria , também temos: ${\ displaystyle - \ beta}$${\ displaystyle \ beta}$

${\ displaystyle \ cos (\ alpha - \ beta) = \ cos \ alpha \ cos (- \ beta) - \ sin \ alpha \ sin (- \ beta),}$

${\ displaystyle \ cos (\ alpha - \ beta) = \ cos \ alpha \ cos \ beta + \ sin \ alpha \ sin \ beta}$

Além disso, usando as fórmulas de ângulos complementares,

${\ displaystyle {\ begin {alinhado} \ cos (\ alpha + \ beta) & = \ sin \ left (\ pi / 2 - (\ alpha + \ beta) \ right) \\ & = \ sin \ left (( \ pi / 2- \ alpha) - \ beta \ right) \\ & = \ sin \ left (\ pi / 2- \ alpha \ right) \ cos \ beta - \ cos \ left (\ pi / 2- \ alpha \ direita) \ sin \ beta \\ & = \ cos \ alpha \ cos \ beta - \ sin \ alpha \ sin \ beta \\\ end {alinhado}}}$

Tangente e cotangente

A partir das fórmulas de seno e cosseno, obtemos

${\ displaystyle \ tan (\ alpha + \ beta) = {\ frac {\ sin (\ alpha + \ beta)} {\ cos (\ alpha + \ beta)}} = {\ frac {\ sin \ alpha \ cos \ beta + \ cos \ alpha \ sin \ beta} {\ cos \ alpha \ cos \ beta - \ sin \ alpha \ sin \ beta}}}$

Dividindo o numerador e o denominador por , obtemos ${\ displaystyle \ cos \ alpha \ cos \ beta}$

${\ displaystyle \ tan (\ alpha + \ beta) = {\ frac {\ tan \ alpha + \ tan \ beta} {1- \ tan \ alpha \ tan \ beta}}}$

Subtraindo de , usando , ${\ displaystyle \ beta}$${\ displaystyle \ alpha}$${\ displaystyle \ tan (- \ beta) = - \ tan \ beta}$

${\ displaystyle \ tan (\ alpha - \ beta) = {\ frac {\ tan \ alpha + \ tan (- \ beta)} {1- \ tan \ alpha \ tan (- \ beta)}} = {\ frac {\ tan \ alpha - \ tan \ beta} {1+ \ tan \ alpha \ tan \ beta}}}$

Da mesma forma, a partir das fórmulas de seno e cosseno, obtemos

${\ displaystyle \ cot (\ alpha + \ beta) = {\ frac {\ cos (\ alpha + \ beta)} {\ sin (\ alpha + \ beta)}} = {\ frac {\ cos \ alpha \ cos \ beta - \ sin \ alpha \ sin \ beta} {\ sin \ alpha \ cos \ beta + \ cos \ alpha \ sin \ beta}}}$

Então, dividindo o numerador e o denominador por , obtemos ${\ displaystyle \ sin \ alpha \ sin \ beta}$

${\ displaystyle \ cot (\ alpha + \ beta) = {\ frac {\ cot \ alpha \ cot \ beta -1} {\ cot \ alpha + \ cot \ beta}}}$

Ou, usando , ${\ displaystyle \ cot \ theta = {\ frac {1} {\ tan \ theta}}}$

${\ displaystyle \ cot (\ alpha + \ beta) = {\ frac {1- \ tan \ alpha \ tan \ beta} {\ tan \ alpha + \ tan \ beta}} = {\ frac {{\ frac {1 } {\ tan \ alpha \ tan \ beta}} - 1} {{\ frac {1} {\ tan \ alpha}} + {\ frac {1} {\ tan \ beta}}}} = {\ frac { \ cot \ alpha \ cot \ beta -1} {\ cot \ alpha + \ cot \ beta}}}$

Usando , ${\ displaystyle \ cot (- \ beta) = - \ cot \ beta}$

${\ displaystyle \ cot (\ alpha - \ beta) = {\ frac {\ cot \ alpha \ cot (- \ beta) -1} {\ cot \ alpha + \ cot (- \ beta)}} = {\ frac {\ cot \ alpha \ cot \ beta +1} {\ cot \ beta - \ cot \ alpha}}}$

Identidades de ângulo duplo

A partir das identidades da soma angular, obtemos

${\ displaystyle \ sin (2 \ theta) = 2 \ sin \ theta \ cos \ theta}$

e

${\ displaystyle \ cos (2 \ theta) = \ cos ^ {2} \ theta - \ sin ^ {2} \ theta}$

As identidades pitagóricas fornecem as duas formas alternativas para a última destas:

${\ displaystyle \ cos (2 \ theta) = 2 \ cos ^ {2} \ theta -1}$

${\ displaystyle \ cos (2 \ theta) = 1-2 \ sin ^ {2} \ theta}$

As identidades da soma dos ângulos também fornecem

${\ displaystyle \ tan (2 \ theta) = {\ frac {2 \ tan \ theta} {1- \ tan ^ {2} \ theta}} = {\ frac {2} {\ cot \ theta - \ tan \ theta}}}$

${\ displaystyle \ cot (2 \ theta) = {\ frac {\ cot ^ {2} \ theta -1} {2 \ cot \ theta}} = {\ frac {\ cot \ theta - \ tan \ theta} { 2}}}$

Também pode ser provado usando a fórmula de Euler

${\ displaystyle e ^ {i \ varphi} = \ cos \ varphi + i \ sin \ varphi}$

A quadratura de ambos os lados produz

${\ displaystyle e ^ {i2 \ varphi} = (\ cos \ varphi + i \ sin \ varphi) ^ {2}}$

Mas substituir o ângulo por sua versão dobrada, que atinge o mesmo resultado no lado esquerdo da equação, produz

${\ displaystyle e ^ {i2 \ varphi} = \ cos 2 \ varphi + i \ sin 2 \ varphi}$

Segue que

${\ displaystyle (\ cos \ varphi + i \ sin \ varphi) ^ {2} = \ cos 2 \ varphi + i \ sin 2 \ varphi}$.

Expandir o quadrado e simplificar no lado esquerdo da equação dá

${\ displaystyle i (2 \ sin \ varphi \ cos \ varphi) + \ cos ^ {2} \ varphi - \ sin ^ {2} \ varphi \ = \ cos 2 \ varphi + i \ sin 2 \ varphi}$.

Porque as partes imaginárias e reais têm que ser as mesmas, ficamos com as identidades originais

${\ displaystyle \ cos ^ {2} \ varphi - \ sin ^ {2} \ varphi \ = \ cos 2 \ varphi}$,

e também

${\ displaystyle 2 \ sin \ varphi \ cos \ varphi = \ sin 2 \ varphi}$.

Identidades de meio ângulo

As duas identidades que fornecem as formas alternativas para cos 2θ levam às seguintes equações:

${\ displaystyle \ cos {\ frac {\ theta} {2}} = \ pm \, {\ sqrt {\ frac {1+ \ cos \ theta} {2}}},}$

${\ displaystyle \ sin {\ frac {\ theta} {2}} = \ pm \, {\ sqrt {\ frac {1- \ cos \ theta} {2}}}.}$

O sinal da raiz quadrada precisa ser escolhido corretamente - observe que se 2 π for adicionado a θ, as quantidades dentro das raízes quadradas não mudam, mas os lados esquerdos das equações mudam de sinal. Portanto, o sinal correto a ser usado depende do valor de θ.

Para a função tan, a equação é:

${\ displaystyle \ tan {\ frac {\ theta} {2}} = \ pm \, {\ sqrt {\ frac {1- \ cos \ theta} {1+ \ cos \ theta}}}.}$

Em seguida, multiplicar o numerador e o denominador dentro da raiz quadrada por (1 + cos θ) e usar as identidades pitagóricas leva a:

${\ displaystyle \ tan {\ frac {\ theta} {2}} = {\ frac {\ sin \ theta} {1+ \ cos \ theta}}.}$

Além disso, se o numerador e o denominador forem multiplicados por (1 - cos θ), o resultado será:

${\ displaystyle \ tan {\ frac {\ theta} {2}} = {\ frac {1- \ cos \ theta} {\ sin \ theta}}.}$

Isso também dá:

${\ displaystyle \ tan {\ frac {\ theta} {2}} = \ csc \ theta - \ cot \ theta.}$

Manipulações semelhantes para a função de berço fornecem:

${\ displaystyle \ cot {\ frac {\ theta} {2}} = \ pm \, {\ sqrt {\ frac {1+ \ cos \ theta} {1- \ cos \ theta}}} = {\ frac { 1+ \ cos \ theta} {\ sin \ theta}} = {\ frac {\ sin \ theta} {1- \ cos \ theta}} = \ csc \ theta + \ cot \ theta.}$

Diversos - a identidade tangente tripla

Se semicírculo (por exemplo , e são os ângulos de um triângulo), ${\ displaystyle \ psi + \ theta + \ phi = \ pi =}$${\ displaystyle \ psi}$${\ displaystyle \ theta}$${\ displaystyle \ phi}$

${\ displaystyle \ tan (\ psi) + \ tan (\ theta) + \ tan (\ phi) = \ tan (\ psi) \ tan (\ theta) \ tan (\ phi).}$

Prova:

${\ displaystyle {\ begin {alinhados} \ psi & = \ pi - \ theta - \ phi \\\ tan (\ psi) & = \ tan (\ pi - \ theta - \ phi) \\ & = - \ tan (\ theta + \ phi) \\ & = {\ frac {- \ tan \ theta - \ tan \ phi} {1- \ tan \ theta \ tan \ phi}} \\ & = {\ frac {\ tan \ theta + \ tan \ phi} {\ tan \ theta \ tan \ phi -1}} \\ (\ tan \ theta \ tan \ phi -1) \ tan \ psi & = \ tan \ theta + \ tan \ phi \ \\ tan \ psi \ tan \ theta \ tan \ phi - \ tan \ psi & = \ tan \ theta + \ tan \ phi \\\ tan \ psi \ tan \ theta \ tan \ phi & = \ tan \ psi + \ tan \ theta + \ tan \ phi \\\ end {alinhado}}}$

Diversos - a identidade tripla cotangente

Se um quarto de círculo, ${\ displaystyle \ psi + \ theta + \ phi = {\ tfrac {\ pi} {2}} =}$

${\ displaystyle \ cot (\ psi) + \ cot (\ theta) + \ cot (\ phi) = \ cot (\ psi) \ cot (\ theta) \ cot (\ phi)}$.

Prova:

Substitua cada um de , e por seus ângulos complementares, para que as cotangentes se transformem em tangentes e vice-versa. ${\ displaystyle \ psi}$${\ displaystyle \ theta}$${\ displaystyle \ phi}$

Dado

${\ displaystyle \ psi + \ theta + \ phi = {\ tfrac {\ pi} {2}}}$

${\ displaystyle \ portanto ({\ tfrac {\ pi} {2}} - \ psi) + ({\ tfrac {\ pi} {2}} - \ theta) + ({\ tfrac {\ pi} {2} } - \ phi) = {\ tfrac {3 \ pi} {2}} - (\ psi + \ theta + \ phi) = {\ tfrac {3 \ pi} {2}} - {\ tfrac {\ pi} {2}} = \ pi}$

portanto, o resultado segue da identidade tangente tripla.

Soma para identidades de produto

• ${\ displaystyle \ sin \ theta \ pm \ sin \ phi = 2 \ sin \ left ({\ frac {\ theta \ pm \ phi} {2}} \ right) \ cos \ left ({\ frac {\ theta \ mp \ phi} {2}} \ right)}$
• ${\ displaystyle \ cos \ theta + \ cos \ phi = 2 \ cos \ left ({\ frac {\ theta + \ phi} {2}} \ right) \ cos \ left ({\ frac {\ theta - \ phi } {2}} \ right)}$
• ${\ displaystyle \ cos \ theta - \ cos \ phi = -2 \ sin \ left ({\ frac {\ theta + \ phi} {2}} \ right) \ sin \ left ({\ frac {\ theta - \ phi} {2}} \ right)}$

Prova de identidades senoidais

Primeiro, comece com as identidades do ângulo de soma:

${\ displaystyle \ sin (\ alpha + \ beta) = \ sin \ alpha \ cos \ beta + \ cos \ alpha \ sin \ beta}$

${\ displaystyle \ sin (\ alpha - \ beta) = \ sin \ alpha \ cos \ beta - \ cos \ alpha \ sin \ beta}$

Ao somar estes juntos,

${\ displaystyle \ sin (\ alpha + \ beta) + \ sin (\ alpha - \ beta) = \ sin \ alpha \ cos \ beta + \ cos \ alpha \ sin \ beta + \ sin \ alpha \ cos \ beta - \ cos \ alpha \ sin \ beta = 2 \ sin \ alpha \ cos \ beta}$

Da mesma forma, subtraindo as duas identidades de ângulo de soma,

${\ displaystyle \ sin (\ alpha + \ beta) - \ sin (\ alpha - \ beta) = \ sin \ alpha \ cos \ beta + \ cos \ alpha \ sin \ beta - \ sin \ alpha \ cos \ beta + \ cos \ alpha \ sin \ beta = 2 \ cos \ alpha \ sin \ beta}$

Deixe e , ${\ displaystyle \ alpha + \ beta = \ theta}$${\ displaystyle \ alpha - \ beta = \ phi}$

${\ displaystyle \ portanto \ alpha = {\ frac {\ theta + \ phi} {2}}}$ e ${\ displaystyle \ beta = {\ frac {\ theta - \ phi} {2}}}$

Substituir e${\ displaystyle \ theta}$${\ displaystyle \ phi}$

${\ displaystyle \ sin \ theta + \ sin \ phi = 2 \ sin \ left ({\ frac {\ theta + \ phi} {2}} \ right) \ cos \ left ({\ frac {\ theta - \ phi } {2}} \ right)}$

${\ displaystyle \ sin \ theta - \ sin \ phi = 2 \ cos \ left ({\ frac {\ theta + \ phi} {2}} \ right) \ sin \ left ({\ frac {\ theta - \ phi } {2}} \ right) = 2 \ sin \ left ({\ frac {\ theta - \ phi} {2}} \ right) \ cos \ left ({\ frac {\ theta + \ phi} {2} }\direito)}$

Portanto,

${\ displaystyle \ sin \ theta \ pm \ sin \ phi = 2 \ sin \ left ({\ frac {\ theta \ pm \ phi} {2}} \ right) \ cos \ left ({\ frac {\ theta \ mp \ phi} {2}} \ right)}$

Prova de identidades de cosseno

Da mesma forma para o cosseno, comece com as identidades do ângulo de soma:

${\ displaystyle \ cos (\ alpha + \ beta) = \ cos \ alpha \ cos \ beta \ - \ sin \ alpha \ sin \ beta}$

${\ displaystyle \ cos (\ alpha - \ beta) = \ cos \ alpha \ cos \ beta + \ sin \ alpha \ sin \ beta}$

Novamente, adicionando e subtraindo

${\ displaystyle \ cos (\ alpha + \ beta) + \ cos (\ alpha - \ beta) = \ cos \ alpha \ cos \ beta \ - \ sin \ alpha \ sin \ beta + \ cos \ alpha \ cos \ beta + \ sin \ alpha \ sin \ beta = 2 \ cos \ alpha \ cos \ beta}$

${\ displaystyle \ cos (\ alpha + \ beta) - \ cos (\ alpha - \ beta) = \ cos \ alpha \ cos \ beta \ - \ sin \ alpha \ sin \ beta - \ cos \ alpha \ cos \ beta - \ sin \ alpha \ sin \ beta = -2 \ sin \ alpha \ sin \ beta}$

Substitua e como antes, ${\ displaystyle \ theta}$${\ displaystyle \ phi}$

${\ displaystyle \ cos \ theta + \ cos \ phi = 2 \ cos \ left ({\ frac {\ theta + \ phi} {2}} \ right) \ cos \ left ({\ frac {\ theta - \ phi } {2}} \ right)}$

${\ displaystyle \ cos \ theta - \ cos \ phi = -2 \ sin \ left ({\ frac {\ theta + \ phi} {2}} \ right) \ sin \ left ({\ frac {\ theta - \ phi} {2}} \ right)}$

Desigualdades

Ilustração das desigualdades seno e tangente.

A figura à direita mostra um setor de um círculo com raio 1. O setor é θ / (2 π ) de todo o círculo, então sua área é θ / 2 . Assumimos aqui que θ < π / 2 .

${\ displaystyle OA = OD = 1}$

${\ displaystyle AB = \ sin \ theta}$

${\ displaystyle CD = \ tan \ theta}$

A área do triângulo OAD é AB / 2 ou sin ( θ ) / 2 . A área do triângulo OCD é CD / 2 ou tan ( θ ) / 2 .

Uma vez que o triângulo OAD está completamente dentro do setor, que por sua vez está completamente dentro do triângulo OCD , temos

${\ displaystyle \ sin \ theta <\ theta <\ tan \ theta.}$

Este argumento geométrico baseia-se em definições de comprimento e área do arco , que atuam como suposições, portanto, é mais uma condição imposta na construção de funções trigonométricas do que uma propriedade provável. Para a função seno, podemos lidar com outros valores. Se θ > π / 2 , então θ > 1 . Mas sen θ ≤ 1 (por causa da identidade pitagórica), então sen θ < θ . Então nós temos

${\ displaystyle {\ frac {\ sin \ theta} {\ theta}} <1 \ \ \ \ mathrm {if} \ \ \ 0 <\ theta.}$

Para valores negativos de θ temos, pela simetria da função seno

${\ displaystyle {\ frac {\ sin \ theta} {\ theta}} = {\ frac {\ sin (- \ theta)} {- \ theta}} <1.}$

Portanto

${\ displaystyle {\ frac {\ sin \ theta} {\ theta}} <1 \ quad {\ text {if}} \ quad \ theta \ neq 0,}$

e

${\ displaystyle {\ frac {\ tan \ theta} {\ theta}}> 1 \ quad {\ text {if}} \ quad 0 <\ theta <{\ frac {\ pi} {2}}.}$

Identidades envolvendo cálculo

Preliminares

${\ displaystyle \ lim _ {\ theta \ to 0} {\ sin \ theta} = 0}$

${\ displaystyle \ lim _ {\ theta \ to 0} {\ cos \ theta} = 1}$

Identidade da razão senoidal e angular

${\ displaystyle \ lim _ {\ theta \ to 0} {\ frac {\ sin \ theta} {\ theta}} = 1}$

Em outras palavras, a função seno é diferenciável em 0 e sua derivada é 1.

Prova: A partir das desigualdades anteriores, temos, para pequenos ângulos

${\ displaystyle \ sin \ theta <\ theta <\ tan \ theta}$,

Portanto,

${\ displaystyle {\ frac {\ sin \ theta} {\ theta}} <1 <{\ frac {\ tan \ theta} {\ theta}}}$,

Considere a desigualdade do lado direito. Desde a

${\ displaystyle \ tan \ theta = {\ frac {\ sin \ theta} {\ cos \ theta}}}$

${\ displaystyle \ portanto 1 <{\ frac {\ sin \ theta} {\ theta \ cos \ theta}}}$

Multiplique por ${\ displaystyle \ cos \ theta}$

${\ displaystyle \ cos \ theta <{\ frac {\ sin \ theta} {\ theta}}}$

Combinando com a desigualdade do lado esquerdo:

${\ displaystyle \ cos \ theta <{\ frac {\ sin \ theta} {\ theta}} <1}$

Levando ao limite como${\ displaystyle \ cos \ theta}$${\ displaystyle \ theta \ a 0}$

${\ displaystyle \ lim _ {\ theta \ to 0} {\ cos \ theta} = 1}$

Portanto,

${\ displaystyle \ lim _ {\ theta \ to 0} {\ frac {\ sin \ theta} {\ theta}} = 1}$

Identidade de cosseno e razão angular

${\ displaystyle \ lim _ {\ theta \ to 0} {\ frac {1- \ cos \ theta} {\ theta}} = 0}$

Prova:

${\ displaystyle {\ begin {align} {\ frac {1- \ cos \ theta} {\ theta}} & = {\ frac {1- \ cos ^ {2} \ theta} {\ theta (1+ \ cos \ theta)}} \\ & = {\ frac {\ sin ^ {2} \ theta} {\ theta (1+ \ cos \ theta)}} \\ & = \ left ({\ frac {\ sin \ theta) } {\ theta}} \ right) \ times \ sin \ theta \ times \ left ({\ frac {1} {1+ \ cos \ theta}} \ right) \\\ end {alinhado}}}$

Os limites dessas três quantidades são 1, 0 e 1/2, portanto, o limite resultante é zero.

Cosseno e identidade da razão quadrada do ângulo

${\ displaystyle \ lim _ {\ theta \ to 0} {\ frac {1- \ cos \ theta} {\ theta ^ {2}}} = {\ frac {1} {2}}}$

Prova:

Como na prova anterior,

${\ displaystyle {\ frac {1- \ cos \ theta} {\ theta ^ {2}}} = {\ frac {\ sin \ theta} {\ theta}} \ times {\ frac {\ sin \ theta} { \ theta}} \ times {\ frac {1} {1+ \ cos \ theta}}.}$

Os limites dessas três quantidades são 1, 1 e 1/2, portanto, o limite resultante é 1/2.

Prova de composições de funções trigonométricas e inversas

Todas essas funções decorrem da identidade trigonométrica pitagórica. Podemos provar, por exemplo, a função

${\ displaystyle \ sin [\ arctan (x)] = {\ frac {x} {\ sqrt {1 + x ^ {2}}}}}$

Prova:

Nós começamos de

${\ displaystyle \ sin ^ {2} \ theta + \ cos ^ {2} \ theta = 1}$

Então, dividimos esta equação por ${\ displaystyle \ cos ^ {2} \ theta}$

${\ displaystyle \ cos ^ {2} \ theta = {\ frac {1} {\ tan ^ {2} \ theta +1}}}$

Em seguida, use a substituição , também use a identidade trigonométrica pitagórica: ${\ displaystyle \ theta = \ arctan (x)}$

${\ displaystyle 1- \ sin ^ {2} [\ arctan (x)] = {\ frac {1} {\ tan ^ {2} [\ arctan (x)] + 1}}}$

Então usamos a identidade ${\ displaystyle \ tan [\ arctan (x)] \ equiv x}$

${\ displaystyle \ sin [\ arctan (x)] = {\ frac {x} {\ sqrt {x ^ {2} +1}}}}$

Veja também

Notas

Referências