Álgebra C * de dimensão aproximada - Approximately finite-dimensional C*-algebra
Em matemática , uma álgebra C * de dimensão aproximadamente finita (AF) é uma álgebra C * que é o limite indutivo de uma sequência de álgebras C * de dimensão finita . A dimensionalidade finita aproximada foi primeiro definida e descrita combinatorialmente por Ola Bratteli . Mais tarde, George A. Elliott deu uma classificação completa de álgebras AF usando o functor K 0, cujo alcance consiste em grupos abelianos ordenados com estrutura de ordem suficientemente boa.
O teorema de classificação para álgebras AF serve como um protótipo para resultados de classificação para classes maiores de álgebras C * finitas e nucleares simples separáveis . Sua prova se divide em duas partes. O invariante aqui é K 0 com sua estrutura de ordem natural; este é um functor . Primeiro, prova-se a existência : um homomorfismo entre invariantes deve elevar-se a um * -homomorfismo de álgebras. Em segundo lugar, um mostra a singularidade : o elevador deve ser único até a equivalência unitária aproximada. A classificação segue então o que é conhecido como o argumento do entrelaçamento . Para álgebras AF unitais, tanto a existência quanto a singularidade seguem do fato do semigrupo de projeções de Murray-von Neumann em uma álgebra AF ser cancelativo.
A contraparte das álgebras AF C * simples no mundo da álgebra de von Neumann são os fatores hiperfinitos, que foram classificados por Connes e Haagerup .
No contexto da geometria e topologia não comutativas , AF C * -álgebras são generalizações não comutativas de C 0 ( X ), onde X é um espaço metrizável totalmente desconectado .
Definição e propriedades básicas
C * -álgebras de dimensão finita
Uma C * -álgebra A de dimensão finita arbitrária assume a seguinte forma, até o isomorfismo:
onde M i denota a álgebra de matriz completa de matrizes i × i .
Até a equivalência unitária, um unital * -homomorfismo Φ: M i → M j é necessariamente da forma
onde r · i = j . Diz-se que o número r é a multiplicidade de Φ. Em geral, um homomorfismo unital entre C * -álgebras de dimensão finita
é especificado, até a equivalência unitária, por uma matriz t × s de multiplicidades parciais ( r l k ) satisfazendo, para todo l
No caso não unital, a igualdade é substituída por ≤. Graficamente, Φ, equivalentemente ( r l k ), pode ser representado por seu diagrama de Bratteli . O diagrama de Bratteli é um grafo direcionado com nós correspondentes a cada n k e m l e o número de setas de n k a m l é a multiplicidade parcial r lk .
Considere a categoria cujos objetos são classes de isomorfismo de C * -álgebras de dimensão finita e cujos morfismos são * -homomorfismos módulo de equivalência unitária. Pela discussão acima, os objetos podem ser vistos como vetores com entradas em N e morfismos são as matrizes de multiplicidade parcial.
Álgebras AF
Álgebra AC * é AF se for o limite direto de uma sequência de álgebras C * de dimensão finita:
onde cada A i é uma C * -álgebra de dimensão finita e os mapas de conexão α i são * -homomorfismos. Vamos supor que cada α i é unital. O sistema indutivo que especifica uma álgebra AF não é único. Sempre se pode cair para uma subsequência. Suprimindo os mapas de conexão, A também pode ser escrito como
O diagrama de Bratteli de A é formado pelos diagramas de Bratteli de { α i } da maneira óbvia. Por exemplo, o triângulo de Pascal , com os nós conectados por setas para baixo apropriadas, é o diagrama de Bratteli de uma álgebra AF. Um diagrama de Bratteli da álgebra CAR é fornecido à direita. As duas setas entre os nós significam que cada mapa de conexão é uma incorporação da multiplicidade 2.
- (Um diagrama de Bratteli da álgebra CAR)
Se uma álgebra AF A = (∪ n A n ) - , então um ideal J em A assume a forma ∪ n ( J ∩ A n ) - . Em particular, J é uma álgebra AF. Dado um diagrama Bratteli de um e alguns subconjuntos S de nodos, a subdiagrama gerado por S dá sistema indutivo que especifica um ideais de um . Na verdade, todo ideal surge dessa maneira.
Devido à presença de unidades de matriz na sequência indutiva, álgebras AF têm a seguinte caracterização local: uma C * -álgebra A é AF se e somente se A for separável e qualquer subconjunto finito de A está "quase contido" em algum dimensional C * -subalgebra.
As projecções em ∪ n A n em forma de facto uma unidade aproximada de um .
É claro que a extensão de uma álgebra C * de dimensão finita por outra álgebra C * de dimensão finita é novamente de dimensão finita. Mais geralmente, a extensão de uma álgebra AF por outra álgebra AF é novamente AF.
Classificação
K 0
O grupo K-teórico K 0 é um invariante das C * -álgebras. Ele tem suas origens na teoria K topológica e serve como o intervalo de um tipo de "função dimensional". Para uma álgebra AF A , K 0 ( A ) pode ser definido como segue. Let H N ( A ) ser o C * -álgebra de n x n matrizes cujas entradas são elementos da Uma . M n ( A ) pode ser incorporado em M n + 1 ( A ) canonicamente, no "canto superior esquerdo". Considere o limite direto algébrico
Denote as projeções (idempotentes auto-adjuntos) nesta álgebra de P ( A ). Dois elementos de p e q são referidos como sendo equivalente Murray-von Neumann , denotada por p ~ q , se p = vv * e q = v * v para alguns isometría parcial v em H ∞ ( A ). É claro que ~ é uma relação de equivalência. Defina uma operação binária + no conjunto de equivalências P ( A ) / ~ por
onde ⊕ é a soma direta ortogonal . Isso torna P ( A ) / ~ um semigrupo que possui a propriedade de cancelamento . Denotamos este semigrupo por K 0 ( A ) + . A execução da construção do grupo Grothendieck dá um grupo abeliano, que é K 0 ( A ).
K 0 ( A ) carrega uma estrutura de ordem natural: dizemos [ p ] ≤ [ q ] se p é Murray-von Neumann equivalente a uma subprojeção de q . Isso torna K 0 ( A ) um grupo ordenado cujo cone positivo é K 0 ( A ) + .
Por exemplo, para uma C * -álgebra de dimensão finita
um tem
Duas características essenciais do mapeamento A ↦ K 0 ( A ) são:
- K 0 é um functor (covariante) . A * -homomorfismo α : A → B entre álgebras de AF induz um homomorfismo de grupo α * : K 0 ( A ) → K 0 ( B ). Em particular, quando A e B são ambos de dimensão finita, α * pode ser identificado com a matriz de multiplicidades parciais de α .
- K 0 respeita os limites diretos. Se A = ∪ n α n ( A n ) - , então K 0 ( A ) é o limite direto ∪ n α n * ( K 0 ( A n )).
O grupo de dimensão
Como M ∞ ( M ∞ ( A )) é isomórfico a M ∞ ( A ), K 0 só pode distinguir álgebras de AF até isomorfismo estável . Por exemplo, M 2 e M 4 são não isomórficas, mas de forma estável isomorfo; K 0 ( H 2 ) = K 0 ( M 4 ) = Z .
Um invariante mais fino é necessário para detectar classes de isomorfismo. Para uma álgebra AF A , definimos a escala de K 0 ( A ), denotada por Γ ( A ), como o subconjunto cujos elementos são representados por projeções em A :
Quando A é unital com unidade 1 A , o elemento K 0 [1 A ] é o elemento máximo de Γ ( A ) e, de fato,
O triplo ( K 0 , K 0 + , Γ ( A )) é chamado o grupo dimensão de Uma . Se A = M s , seu grupo de dimensão é ( Z , Z + , {1, 2, ..., s }).
Um homomorfismo de grupo entre o grupo de dimensão é considerado contrativo se ele preserva a escala. O grupo de duas dimensões é considerado isomórfico se houver um isomorfismo de grupo de contração entre eles.
O grupo de dimensão retém as propriedades essenciais de K 0 :
- A * -homomorfismo α : A → B entre as álgebras de AF de fato induz um homomorfismo de grupo de contração α * nos grupos de dimensão. Quando A e B são ambos finito-dimensionais, correspondendo a cada matriz de multiplicidades parciais ψ , existe um único, até equivalência unitária, * -homomorfismo α : A → B tal que α * = ψ .
- Se A = ∪ n α n ( A n ) - , então o grupo de dimensões de A é o limite direto daqueles de A n .
Teorema de Elliott
O teorema de Elliott diz que o grupo dimensional é um invariante completo das álgebras AF: duas álgebras AF A e B são isomórficas se e somente se seus grupos dimensionais forem isomórficos.
Dois fatos preliminares são necessários antes que se possa esboçar uma prova do teorema de Elliott. O primeiro resume a discussão acima sobre C * -álgebras de dimensão finita.
Lema Para duas C * -álgebras A e B de dimensão finita , e um homomorfismo contrativo ψ : K 0 ( A ) → K 0 ( B ), existe um * -homomorfismo φ : A → B tal que φ * = ψ , e φ é único até equivalência unitária.
O lema pode ser estendido para o caso em que B é AF. Um mapa ψ no nível de K 0 pode ser "movido para trás", no nível das álgebras, para algum estágio finito no sistema indutivo.
Lema Seja A dimensão finita e B AF, B = (∪ n B n ) - . Deixe β m ser o homomorphism canónica de B m em B . Então, para qualquer homomorfismo contrativo ψ : K 0 ( A ) → K 0 ( B ), existe um * -homomorfismo φ : A → B m tal que β m * φ * = ψ , e φ é único até a equivalência unitária em B .
A prova do lema é baseada na simples observação de que K 0 ( A ) é finitamente gerado e, uma vez que K 0 respeita limites diretos, K 0 ( B ) = ∪ n β n * K 0 ( B n ).
Teorema (Elliott) Duas álgebras AF A e B são isomórficas se e somente se seus grupos dimensionais ( K 0 ( A ), K 0 + ( A ), Γ ( A )) e ( K 0 ( B ), K 0 + ( B ), Γ ( B )) são isomórficos.
O ponto crucial da prova tornou-se conhecido como o argumento entrelaçado de Elliott . Dado um isomorfismo entre grupos de dimensões, constrói-se um diagrama de triângulos comutáveis entre os sistemas diretos de A e B aplicando o segundo lema.
Esboçamos a prova para a parte não trivial do teorema, correspondendo à seqüência de diagramas comutativos à direita.
Seja Φ: ( K 0 ( A ), K 0 + ( A ), Γ ( A )) → ( K 0 ( B ), K 0 + ( B ), Γ ( B )) um isomorfismo de grupo de dimensões.
- Considere a composição dos mapas Φ α 1 * : K 0 ( A 1 ) → K 0 ( B ). Pelo lema anterior, existe B 1 e um * -homomorfismo φ 1 : A 1 → B 1 tal que o primeiro diagrama à direita comuta.
- O mesmo argumento aplicado a β 1 * Φ −1 mostra que o segundo diagrama comuta para algum A 2 .
- A comparação dos diagramas 1 e 2 resulta no diagrama 3.
- Usando a propriedade do limite direto e movendo A 2 mais para baixo se necessário, obtemos o diagrama 4, um triângulo comutativo no nível de K 0 .
- Para álgebras de dimensão finita, dois * -homomorfismos induzem o mesmo mapa em K 0 se e somente se eles forem equivalentes unitários. Portanto, ao compor ψ 1 com uma conjugação unitária, se necessário, temos um triângulo comutativo no nível das álgebras.
- Por indução, temos um diagrama de triângulos comutantes, conforme indicado no último diagrama. O mapa φ : A → B é o limite direto da sequência { φ n }. Seja ψ : B → A é o limite direto da sequência { ψ n }. É claro que φ e ψ são inversos mútuos. Portanto, A e B são isomórficos.
Além disso, no nível de K 0 , o diagrama adjacente comuta para cada k . Pela unicidade do limite direto dos mapas, φ * = Φ.
Teorema Effros-Handelman-Shen
O grupo de dimensões de uma álgebra AF é um grupo de Riesz . O teorema Effros-Handelman-Shen diz que o inverso é verdadeiro. Cada grupo de Riesz, com uma determinada escala, surge como o grupo de dimensões de alguma álgebra AF. Isso especifica o intervalo do functor de classificação K 0 para álgebras AF e completa a classificação.
Grupos Riesz
Um grupo G com uma ordem parcial é chamado de grupo ordenado . O conjunto de G + de elementos ≥ 0 é chamado de cone positiva de L . Diz-se que G não é perfurado se k · g ∈ G + implica g ∈ G + .
A seguinte propriedade é chamada de propriedade de decomposição de Riesz : se x , y i ≥ 0 e x ≤ Σ y i , então existe x i ≥ 0 tal que x = Σ x i , e x i ≤ y i para cada i .
Um grupo Riesz ( G , G + ) é um grupo ordenado não perfurado e que possui a propriedade de decomposição de Riesz.
É claro que se A é finito-dimensional, ( K 0 , K 0 + ) é um grupo de Riesz, onde Z k é dada a ordem de entrada. As duas propriedades dos grupos de Riesz são preservadas por limites diretos, assumindo que a estrutura de ordem no limite direto vem daquelas no sistema indutivo. Então, ( K 0 , K 0 + ) é um grupo de Riesz para uma FA álgebra Uma .
Um passo fundamental para o teorema Effros-Handelman-Shen é o fato de que todo grupo de Riesz é o limite direto de Z k 's, cada um com a estrutura de ordem canônica. Isso depende do seguinte lema técnico, às vezes referido como o critério de Shen na literatura.
Lema Seja ( G , G + ) um grupo de Riesz, ϕ : ( Z k , Z k + ) → ( G , G + ) um homomorfismo positivo. Então existem os mapas σ e ψ , conforme indicado no diagrama adjacente, tais que ker ( σ ) = ker ( ϕ ).
Corolário Cada grupo de Riesz ( G , G + ) pode ser expresso como um limite direto
onde todos os homomorfismos de conexão no sistema direcionado do lado direito são positivos.
O teorema
Teorema Se ( G , G + ) é um grupo de Riesz contável com escala Γ ( G ), então existe uma álgebra AF A tal que ( K 0 , K 0 + , Γ ( A )) = ( G , G + , Γ ( G )). Em particular, se Γ ( G ) = [0, u G ] com elemento máximo u G , então A é unital com [1 A ] = [ u G ].
Consideremos primeiro o caso especial onde Γ ( L ) = [0, L L ] com o elemento máxima u L . Suponha
Descendo para uma subsequência, se necessário, deixe
onde φ 1 ( u 1 ) = u G para algum elemento u 1 . Agora considere o ideal de ordem G 1 gerado por u 1 . Como cada H 1 tem a estrutura de ordem canônica, G 1 é uma soma direta de Z 's (com o número de cópias possíveis menor do que em H 1 ). Portanto, isso nos dá uma álgebra de dimensão finita A 1 cujo grupo de dimensões é ( G 1 G 1 + , [0, u 1 ]). Em seguida, mova u 1 para frente definindo u 2 = φ 12 ( u 1 ). Novamente u 2 determina uma álgebra de dimensão finita A 2 . Existe um homomorfismo α 12 correspondente, tal que α 12 * = φ 12 . A indução dá um sistema direcionado
cujo K 0 é
com escala
Isso prova o caso especial.
Um argumento semelhante se aplica em geral. Observe que a escala é por definição um conjunto direcionado . Se Γ ( G ) = { v k }, pode-se escolher u k ∈ Γ ( G ) tal que u k ≥ v 1 ... v k . O mesmo argumento acima prova o teorema.
Exemplos
Por definição, as álgebras uniformemente hiperfinidas são AF e unitais . Seus grupos de dimensão são os subgrupos de Q . Por exemplo, para as matrizes 2 × 2 M 2 , K 0 ( M 2 ) é o grupo de números racionais da formauma/2para um em Z . A escala é Γ ( M 2 ) = {0,1/2, 1}. Para a álgebra CAR A , K 0 ( A ) é o grupo de racionais diádicos com escala K 0 ( A ) ∩ [0, 1], com 1 = [1 A ]. Todos esses grupos são simples , de certa forma apropriados para grupos ordenados. Assim, as álgebras UHF são álgebras C * simples. Em geral, os grupos que não são densos em Q são os grupos dimensionais de M k para algum k .
As álgebras C * comutativas, que foram caracterizadas por Gelfand , são AF precisamente quando o espectro está totalmente desconectado . As funções contínuas C ( X ) no conjunto Cantor X são um exemplo.
Programa de classificação de Elliott
Foi proposto por Elliott que outras classes de C * -álgebras podem ser classificáveis por invariantes da teoria K. Para uma C * -álgebra A , o invariante de Elliott é definido como
onde T + ( A ) são os funcionais lineares positivos traciais na topologia fraca- *, e ρ A é o emparelhamento natural entre T + ( A ) e K 0 ( A ).
A conjectura original de Elliott afirmava que o invariante de Elliott classifica álgebras C * nucleares separáveis unitais simples.
Na literatura, pode-se encontrar várias conjecturas desse tipo com os invariantes de Elliott modificados / refinados correspondentes.
Álgebras de Von Neumann
Em um contexto relacionado, uma álgebra de von Neumann de dimensão aproximadamente finita , ou hiperfinita , é aquela com um predual separável e contém uma álgebra AF C * fracamente densa. Murray e von Neumann mostraram que, até o isomorfismo, existe um único fator hiperfinito tipo II 1 . Connes obteve o resultado análogo para o fator II ∞ . Powers exibiu uma família de fatores hiperfinitos não isomórficos do tipo III com cardinalidade do contínuo. Hoje temos uma classificação completa de fatores hiperfinitos.
Notas
Referências
- Bratteli, Ola. (1972), Inductive limit of finite dimensional C * -algebras , Trans. Amer. Matemática. Soc. 171 , 195-234.
- Davidson, KR (1996), C * -algebras by Example , Field Institute Monographs 6 , American Mathematical Society.
- Effros, EG , Handelman, DE, e Shen CL (1980), Dimension groups and their affine representations , Amer. J. Math. 102 , 385-402.
- Elliott, GA (1976), On the Classification of Inductive Limits of Sequences of Semisimple Finite-Dimensional Algebras , J. Algebra 38 , 29-44.
- Elliott, GA e Toms, AS (2008), Propriedades de regularidade no programa de classificação para álgebras C separáveis , Bull. Amer. Matemática. Soc. 45 , 229-245.
- Fillmore, PA (1996), A User's Guide for Operator Algebras , Wiley-Interscience.
- Rørdam, M. (2002), Classification of Nuclear C * -Algebras , Encyclopaedia of Mathematical Sciences 126 , Springer-Verlag.
links externos
- "AF-algebra" , Encyclopedia of Mathematics , EMS Press , 2001 [1994]









![[p] + [q] = [p \ oplus q]](https://wikimedia.org/api/rest_v1/media/math/render/svg/fc79b9f4852ef6776ee2dfcee7bea2adddc57af3)


![\ Gamma (A) = \ {[p] \, | \, p ^ {*} = p ^ {2} = p \ em A \}.](https://wikimedia.org/api/rest_v1/media/math/render/svg/a6f3665f106405b46b7ecc584f0d83117e120962)
![\ Gamma (A) = \ {x \ in K_ {0} (A) \, | \, 0 \ leq x \ leq [1_ {A}] \}.](https://wikimedia.org/api/rest_v1/media/math/render/svg/6fa4f593f27c0ce5f96ecb21ba230d348090c12d)

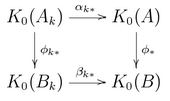






![\ cup _ {k} \ phi _ {k} [0, u_ {k}] = [0, u_ {G}].](https://wikimedia.org/api/rest_v1/media/math/render/svg/8e89f1f57e8019e5b4285cdb37cc26b8779c2d15)
