Regressão em direção à média - Regression toward the mean

Configuração experimental de Galton (Fig.8)

Em estatística , a regressão em direção à média (também chamada de regressão à média , reversão à média e reversão à mediocridade ) é o fenômeno que surge se um ponto de amostra de uma variável aleatória for extremo (quase um outlier ), caso em que um o ponto futuro provavelmente estará mais próximo da média ou da média . Para evitar fazer inferências incorretas , a regressão em direção à média deve ser considerada ao projetar experimentos científicos e interpretar dados.

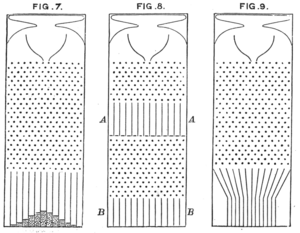
As condições sob as quais ocorre a regressão em direção à média dependem da maneira como o termo é definido matematicamente. O polímata britânico Sir Francis Galton observou o fenômeno pela primeira vez no contexto da regressão linear simples de pontos de dados. Galton desenvolveu o seguinte modelo: os pellets caem através de um quincunce para formar uma distribuição normal centrada diretamente sob seu ponto de entrada. Essas pelotas podem então ser liberadas para uma segunda galeria correspondendo a uma segunda medição. Galton então fez a pergunta inversa: "De onde vieram essas pelotas?"

A resposta não foi " em média diretamente acima " . Em vez disso, era " em média, mais para o meio " , pela simples razão de que havia mais pelotas acima dele em direção ao meio que podiam vagar para a esquerda do que havia no extremo esquerdo que poderia vagar para a direita, para dentro.

Por ser uma abordagem menos restritiva, a regressão à média pode ser definida para qualquer distribuição bivariada com distribuições marginais idênticas . Existem duas dessas definições. Uma definição está de acordo com o uso comum do termo "regressão em direção à média". Nem todas essas distribuições bivariadas mostram regressão em direção à média sob esta definição. No entanto, todas essas distribuições bivariadas mostram regressão em direção à média sob a outra definição.

Jeremy Siegel usa o termo "retorno à média" para descrever uma série temporal financeira na qual "os retornos podem ser muito instáveis ​​no curto prazo, mas muito estáveis ​​no longo prazo". Mais quantitativamente, é aquele em que o desvio padrão dos retornos médios anuais diminui mais rápido do que o inverso do período de manutenção, implicando que o processo não é uma caminhada aleatória , mas que os períodos de retornos mais baixos são sistematicamente seguidos por períodos de compensação de retornos mais elevados , como é o caso de muitos negócios sazonais, por exemplo.

Contexto conceitual

Considere um exemplo simples: uma classe de alunos faz um teste verdadeiro / falso de 100 itens sobre um assunto. Suponha que todos os alunos escolham aleatoriamente em todas as questões. Então, a pontuação de cada aluno seria uma realização de um conjunto de variáveis ​​aleatórias independentes e distribuídas de forma idêntica , com uma média esperada de 50. Naturalmente, alguns alunos irão pontuar substancialmente acima de 50 e alguns substancialmente abaixo de 50 apenas por acaso. Se alguém selecionar apenas os 10% de pontuação mais altos dos alunos e dar a eles um segundo teste no qual eles escolhem novamente aleatoriamente em todos os itens, a pontuação média seria novamente próxima de 50. Assim, a média desses alunos "regrediria "todo o caminho de volta à média de todos os alunos que fizeram o teste original. Não importa a pontuação do aluno no teste original, a melhor previsão de sua pontuação no segundo teste é 50.

Se a escolha das respostas para as perguntas do teste não fosse aleatória - ou seja, se não houvesse sorte (boa ou ruim) ou adivinhação aleatória envolvida nas respostas fornecidas pelos alunos - então todos os alunos deveriam ter a mesma pontuação no segundo teste que eles pontuado no teste original, e não haveria regressão em direção à média.

As situações mais realistas situam-se entre esses dois extremos: por exemplo, pode-se considerar as notas dos exames como uma combinação de habilidade e sorte . Nesse caso, o subconjunto de alunos com pontuação acima da média seria composto por aqueles que eram qualificados e não tinham muita má sorte, junto com aqueles que não eram qualificados, mas eram extremamente sortudos. Em um novo teste deste subconjunto, os não qualificados dificilmente repetirão seu golpe de sorte, enquanto os qualificados terão uma segunda chance de ter azar. Portanto, é improvável que aqueles que se saíram bem anteriormente se sairão tão bem no segundo teste, mesmo que o original não possa ser replicado.

A seguir, um exemplo desse segundo tipo de regressão em direção à média. Uma turma de alunos faz duas edições do mesmo teste em dois dias sucessivos. Freqüentemente, tem sido observado que os piores desempenhos no primeiro dia tendem a melhorar suas pontuações no segundo dia, e os melhores desempenhos no primeiro dia tendem a ter pior desempenho no segundo dia. O fenômeno ocorre porque as pontuações dos alunos são determinadas em parte pela capacidade subjacente e em parte pelo acaso. Para o primeiro teste, alguns terão sorte e pontuarão mais do que sua capacidade, e alguns terão azar e pontuarão menos do que sua capacidade. Alguns dos alunos sortudos no primeiro teste terão sorte novamente no segundo teste, mas a maioria deles terá (para eles) notas médias ou abaixo da média. Portanto, um aluno que teve sorte e superou suas habilidades no primeiro teste tem mais probabilidade de ter uma pontuação pior no segundo teste do que uma pontuação melhor. Da mesma forma, os alunos que, infelizmente, pontuam menos do que sua capacidade no primeiro teste, tenderão a ver suas pontuações aumentarem no segundo teste. Quanto maior a influência da sorte na produção de um evento extremo, menos provável que a sorte se repita em vários eventos.

Outros exemplos

Se seu time favorito ganhou o campeonato no ano passado, o que isso significa para as chances de vitória na próxima temporada? Na medida em que este resultado se deve à habilidade (equipe em boas condições, com um técnico de ponta, etc.), sua vitória sinaliza que é mais provável que voltem a vencer no próximo ano. Mas quanto maior a extensão disso é devido à sorte (outras equipes envolvidas em um escândalo de drogas, empate favorável, escolhas de recrutamento acabaram sendo produtivas, etc.), menos provável é que eles voltem a vencer no próximo ano.

Se um teste médico sugerir que um determinado medicamento ou tratamento está superando todos os outros tratamentos para uma condição, então, em um segundo teste, é mais provável que o medicamento ou tratamento com desempenho superior tenha um desempenho mais próximo da média.

Se uma organização empresarial tiver um trimestre altamente lucrativo, apesar das razões subjacentes para seu desempenho permanecerem inalteradas, é provável que ela se saia menos bem no próximo trimestre.

Os jogadores de beisebol que jogaram bem em sua temporada de estreia provavelmente se sairão pior na segunda; a " queda do segundo ano ". Da mesma forma, a regressão em direção à média é uma explicação para o feitiço da capa da Sports Illustrated - períodos de desempenho excepcional que resulta em um recurso de capa são provavelmente seguidos por períodos de desempenho mais medíocre, dando a impressão de que aparecer na capa causa o declínio do atleta .

História

O conceito de regressão vem da genética e foi popularizado por Sir Francis Galton durante o final do século 19 com a publicação de Regressão para a mediocridade na estatura hereditária . Galton observou que características extremas (por exemplo, altura) nos pais não são passadas completamente para seus filhos. Em vez disso, as características da prole regridem para um ponto medíocre (um ponto que desde então foi identificado como a média). Ao medir a altura de centenas de pessoas, ele foi capaz de quantificar a regressão à média e estimar o tamanho do efeito. Galton escreveu que "a regressão média da prole é uma fração constante de seus respectivos desvios parental médio". Isso significa que a diferença entre uma criança e seus pais para alguma característica é proporcional ao desvio de seus pais em relação às pessoas típicas da população. Se seus pais forem cinco centímetros mais altos do que as médias de homens e mulheres, então, em média, a prole será mais baixa do que seus pais por algum fator (que, hoje, chamaríamos de um menos o coeficiente de regressão ) vezes duas polegadas. Para a altura, Galton estimou esse coeficiente em cerca de 2/3: a altura de um indivíduo será medida em torno de um ponto médio que é dois terços do desvio dos pais em relação à média da população.

Galton cunhou o termo "regressão" para descrever um fato observável na herança de traços genéticos quantitativos multifatoriais : a saber, que a prole dos pais que estão nas caudas da distribuição tenderá a ficar mais perto do centro, a média, de a distribuição. Ele quantificou essa tendência e, ao fazê-lo, inventou a análise de regressão linear , lançando assim as bases para grande parte da modelagem estatística moderna. Desde então, o termo "regressão" assumiu uma variedade de significados e pode ser usado por estatísticos modernos para descrever fenômenos de viés de amostragem que pouco têm a ver com as observações originais de Galton no campo da genética.

Embora sua análise matemática estivesse correta, sabe-se que a explicação biológica de Galton para o fenômeno de regressão que observou está incorreta. Ele declarou: "Uma criança herda em parte de seus pais, em parte de seus ancestrais. Em termos gerais, quanto mais sua genealogia retrocede, mais numerosa e variada se tornará sua ancestralidade, até que eles deixem de ser diferentes de qualquer amostra igualmente numerosa tirada ao acaso da corrida em geral. " Isso é incorreto, uma vez que a criança recebe sua composição genética exclusivamente de seus pais. Não há salto de geração no material genético: qualquer material genético de ancestrais anteriores deve ter passado pelos pais (embora possa não ter sido expresso neles). O fenômeno é melhor compreendido se assumirmos que a característica herdada (por exemplo, altura) é controlada por um grande número de genes recessivos . Indivíduos excepcionalmente altos devem ser homozigotos para mutações de altura aumentada em uma grande proporção desses loci . Mas os loci que carregam essas mutações não são necessariamente compartilhados entre dois indivíduos altos e, se esses indivíduos se acasalarem, sua prole será, em média, homozigótica para mutações "altas" em menos loci do que qualquer um de seus pais. Além disso, a altura não é inteiramente determinada geneticamente, mas também está sujeita a influências ambientais durante o desenvolvimento, o que torna os filhos de pais excepcionais ainda mais propensos a estar mais próximos da média do que seus pais.

Este fenômeno genético populacional de regressão à média é melhor pensado como uma combinação de um processo de herança binomialmente distribuído mais influências ambientais normalmente distribuídas. Em contraste, o termo "regressão à média" agora é frequentemente usado para descrever o fenômeno pelo qual um viés de amostragem inicial pode desaparecer à medida que amostras novas, repetidas ou maiores exibem médias de amostra que estão mais próximas da verdadeira média da população subjacente.

Importância

A regressão em direção à média é uma consideração significativa no planejamento de experimentos .

Tome um exemplo hipotético de 1.000 indivíduos de idade semelhante que foram examinados e pontuados quanto ao risco de sofrer um ataque cardíaco. As estatísticas podem ser usadas para medir o sucesso de uma intervenção nas 50 pessoas classificadas como de maior risco. A intervenção pode ser uma mudança na dieta, exercícios ou um tratamento medicamentoso. Mesmo que as intervenções sejam inúteis, espera-se que o grupo de teste mostre uma melhora em seu próximo exame físico, por causa da regressão em direção à média. A melhor maneira de combater esse efeito é dividir o grupo aleatoriamente em um grupo de tratamento que recebe o tratamento e um grupo de controle que não recebe . O tratamento seria então considerado eficaz apenas se o grupo de tratamento melhorar mais do que o grupo de controle.

Alternativamente, um grupo de crianças desfavorecidas pode ser testado para identificar aquelas com maior potencial para a faculdade. O 1% do topo poderia ser identificado e fornecido com cursos especiais de enriquecimento, tutoria, aconselhamento e computadores. Mesmo que o programa seja eficaz, suas pontuações médias podem ser menores quando o teste é repetido um ano depois. No entanto, nessas circunstâncias, pode ser considerado antiético ter um grupo de controle de crianças desfavorecidas cujas necessidades especiais são ignoradas. Um cálculo matemático para o encolhimento pode ajustar esse efeito, embora não seja tão confiável quanto o método do grupo de controle (veja também o exemplo de Stein ).

O efeito também pode ser explorado para inferência e estimativa geral. O lugar mais quente do país hoje tem mais probabilidade de ser mais frio amanhã do que mais quente, em comparação com hoje. O fundo mútuo de melhor desempenho nos últimos três anos tem mais probabilidade de ver o declínio do desempenho relativo do que melhorar nos próximos três anos. O ator de Hollywood mais bem-sucedido deste ano provavelmente terá menos bruto do que mais bruto em seu próximo filme. O jogador de beisebol com a maior média de rebatidas no intervalo do All-Star tem mais probabilidade de ter uma média mais baixa do que uma média mais alta na segunda metade da temporada.

Mal-entendidos

O conceito de regressão em direção à média pode ser mal utilizado com muita facilidade.

No exemplo de teste do aluno acima, foi assumido implicitamente que o que estava sendo medido não mudou entre as duas medições. Suponha, no entanto, que o curso foi aprovado / reprovado e os alunos foram obrigados a pontuar acima de 70 em ambos os testes para serem aprovados. Assim, os alunos que pontuaram abaixo de 70 na primeira vez não teriam incentivo para se sair bem e poderiam pontuar pior, em média, na segunda vez. Os alunos com pouco mais de 70 anos, por outro lado, teriam um forte incentivo para estudar e se concentrar durante a realização do teste. Nesse caso, pode-se ver o movimento saindo de 70, as pontuações abaixo dele ficando mais baixas e as pontuações acima ficando mais altas. É possível que mudanças entre os tempos de medição aumentem, compensem ou invertam a tendência estatística de regredir em direção à média.

A regressão estatística em direção à média não é um fenômeno causal . Um aluno com a pior pontuação no teste no primeiro dia não necessariamente aumentará sua pontuação substancialmente no segundo dia devido ao efeito. Em média, os piores pontuadores melhoram, mas isso só é verdade porque os piores pontuadores têm mais probabilidade de ter tido azar do que sorte. Na medida em que uma pontuação seja determinada aleatoriamente, ou que uma pontuação tenha variação aleatória ou erro, ao invés de ser determinada pela capacidade acadêmica do aluno ou ser um "valor verdadeiro", o fenômeno terá efeito. Um erro clássico a esse respeito foi na educação. Os alunos que receberam elogios por um bom trabalho tiveram um desempenho pior na próxima medida e os alunos que foram punidos por um bom trabalho tiveram um desempenho melhor na próxima medida. Os educadores decidiram parar de elogiar e continuar punindo com base nisso. Tal decisão foi um erro, porque a regressão em direção à média não é baseada em causa e efeito, mas sim no erro aleatório em uma distribuição natural em torno de uma média.

Embora as medidas individuais extremas regridam em direção à média, a segunda amostra de medidas não estará mais perto da média do que a primeira. Considere os alunos novamente. Suponha que a tendência de indivíduos extremos seja regredir 10% do caminho em direção à média de 80, então um aluno que marcou 100 no primeiro dia deve marcar 98 no segundo dia, e um aluno que marcou 70 no primeiro dia deve pontuação 71 no segundo dia. Essas expectativas estão mais próximas da média do que as pontuações do primeiro dia. Mas as pontuações do segundo dia variam de acordo com suas expectativas; alguns serão mais altos e alguns serão mais baixos. Além disso, indivíduos que medem muito perto da média devem esperar afastar-se da média. O efeito é o inverso exato da regressão em direção à média e o compensa exatamente. Portanto, para indivíduos extremos, esperamos que a segunda pontuação esteja mais perto da média do que a primeira pontuação, mas para todos os indivíduos, esperamos que a distribuição das distâncias da média seja a mesma em ambos os conjuntos de medidas.

Relacionado ao ponto acima, a regressão em direção à média funciona igualmente bem em ambas as direções. Esperamos que o aluno com a maior pontuação de teste no segundo dia tenha se saído pior no primeiro dia. E se compararmos o melhor aluno do primeiro dia com o melhor aluno do segundo dia, independentemente de ser o mesmo indivíduo ou não, há uma tendência de regredir para a média indo em qualquer direção. Esperamos que as melhores pontuações em ambos os dias estejam igualmente longe da média.

Falácias de regressão

Muitos fenômenos tendem a ser atribuídos a causas erradas quando a regressão à média não é levada em consideração.

Um exemplo extremo é o livro de Horace Secrist , de 1933, The Triumph of Mediocrity in Business , no qual o professor de estatística coletou montanhas de dados para provar que as taxas de lucro de empresas competitivas tendem à média ao longo do tempo. Na verdade, esse efeito não existe; a variabilidade das taxas de lucro é quase constante ao longo do tempo. Secrist havia apenas descrito a regressão comum em direção à média. Um crítico exasperado, Harold Hotelling , comparou o livro a "provar a tabuada ao organizar os elefantes em linhas e colunas, e então fazer o mesmo com vários outros tipos de animais".

O cálculo e a interpretação das "pontuações de melhoria" em testes educacionais padronizados em Massachusetts provavelmente fornecem outro exemplo da falácia da regressão. Em 1999, as escolas receberam metas de melhoria. Para cada escola, o Departamento de Educação tabulou a diferença na pontuação média alcançada pelos alunos em 1999 e em 2000. Notou-se rapidamente que a maioria das escolas com pior desempenho havia atingido suas metas, o que o Departamento de Educação considerou como confirmação de a solidez de suas políticas. No entanto, também foi notado que muitas das escolas supostamente melhores da Comunidade, como a Brookline High School (com 18 finalistas do National Merit Scholarship) foram declaradas reprovadas. Como em muitos casos envolvendo estatísticas e políticas públicas, a questão é debatida, mas "notas de melhoria" não foram anunciadas nos anos subsequentes e os resultados parecem ser um caso de regressão à média.

O psicólogo Daniel Kahneman , ganhador do Prêmio Nobel Memorial de Ciências Econômicas de 2002 , apontou que a regressão à média pode explicar por que as repreensões parecem melhorar o desempenho, enquanto os elogios parecem sair pela culatra.

Tive a experiência Eureka mais satisfatória de minha carreira ao tentar ensinar instrutores de vôo que elogiar é mais eficaz do que punir por promover o aprendizado de habilidades. Quando terminei meu discurso entusiasmado, um dos instrutores mais experientes da platéia levantou a mão e fez seu próprio discurso curto, que começou admitindo que o reforço positivo poderia ser bom para os pássaros, mas negou que fosse o ideal para cadetes de vôo. Ele disse: "Em muitas ocasiões, elogiei os cadetes de vôo pela execução limpa de alguma manobra acrobática e, em geral, quando eles tentam de novo, fazem pior. Por outro lado, muitas vezes gritei com os cadetes por má execução e em geral, eles farão melhor da próxima vez. Portanto, não nos diga que o reforço funciona e a punição não, porque ocorre o oposto. " Foi um momento de alegria, em que compreendi uma verdade importante sobre o mundo: porque tendemos a recompensar os outros quando fazem bem e puni-los quando fazem mal, e porque há regressão ao meio, faz parte do humano condição de que sejamos estatisticamente punidos por recompensar os outros e recompensados ​​por puni-los. Eu imediatamente organizei uma demonstração em que cada participante jogava duas moedas em um alvo pelas costas, sem qualquer feedback. Medimos as distâncias do alvo e pudemos ver que aqueles que se saíram melhor na primeira vez pioraram principalmente na segunda tentativa, e vice-versa. Mas eu sabia que essa demonstração não desfaria os efeitos da exposição ao longo da vida a uma contingência perversa.

Para colocar a história de Kahneman em termos simples, quando alguém comete um erro grave, seu desempenho mais tarde geralmente retorna ao seu nível médio de qualquer maneira. Isso parecerá um avanço e uma "prova" de uma crença de que é melhor criticar do que elogiar (sustentada principalmente por quem está disposto a criticar naquele momento "baixo"). Na situação contrária, quando acontece de um desempenho muito acima da média, seu desempenho também tenderá a retornar ao seu nível médio mais tarde; a mudança será percebida como uma deterioração e qualquer elogio inicial após a primeira apresentação como a causa dessa deterioração. Só porque criticar ou elogiar precede a regressão à média, o ato de criticar ou elogiar é falsamente atribuído à causalidade. A falácia de regressão também é explicado no Rolf Dobelli é a arte de pensar claramente .

As políticas de aplicação da lei do Reino Unido encorajaram a localização visível de radares estáticos ou móveis em pontos negros de acidentes . Esta política foi justificada pela percepção de que há uma redução correspondente de acidentes rodoviários graves após a instalação de uma câmera. No entanto, os estatísticos apontaram que, embora haja um benefício líquido em vidas salvas, deixar de levar em consideração os efeitos da regressão à média resulta na superestimação dos efeitos benéficos.

Os analistas estatísticos há muito reconheceram o efeito da regressão à média nos esportes; eles até têm um nome especial para isso: a " crise do segundo ano ". Por exemplo, Carmelo Anthony da NBA 's Denver Nuggets teve uma temporada de estreia notável em 2004. Isso foi tão maravilhoso que ele não poderia ser esperado para repeti-lo: em 2005, os números de Anthony caiu de sua temporada de estreia. As razões para a "queda do segundo ano" abundam, já que os esportes dependem de ajustes e contra-ajustes, mas a excelência baseada na sorte para um novato é uma razão tão boa quanto qualquer outra. A regressão à média no desempenho esportivo também pode explicar o aparente " azar da capa da Sports Illustrated " e a " Maldição Madden ". John Hollinger tem um nome alternativo para o fenômeno da regressão à média: a "regra do acaso", enquanto Bill James a chama de "Princípio do Plexiglass".

Como a tradição popular tem se concentrado na regressão em direção à média como um relato do declínio do desempenho dos atletas de uma temporada para a seguinte, ela geralmente negligencia o fato de que tal regressão também pode ser responsável pela melhoria do desempenho. Por exemplo, se olharmos para a média de rebatidas dos jogadores da Liga Principal de Beisebol em uma temporada, aqueles cuja média de rebatidas estava acima da média da liga tendem a regredir para baixo em direção à média no ano seguinte, enquanto aqueles cuja média de rebatidas estava abaixo da média tendem a progresso para cima em direção à média no ano seguinte.

Outros fenômenos estatísticos

A regressão em direção à média simplesmente diz que, após um evento aleatório extremo, o próximo evento aleatório provavelmente será menos extremo. Em nenhum sentido o evento futuro "compensa" ou "compensa" o evento anterior, embora isso seja assumido na falácia do jogador (e na lei variante das médias ). Da mesma forma, a lei dos grandes números afirma que, a longo prazo, a média tenderá para o valor esperado, mas não faz qualquer afirmação sobre as tentativas individuais. Por exemplo, após uma sequência de 10 caras no lançamento de uma moeda justa (um evento raro e extremo), a regressão à média afirma que a próxima sequência de caras provavelmente será menor que 10, enquanto a lei dos grandes números afirma que a longo prazo, esse evento provavelmente terá uma média, e a fração média de caras tenderá a 1/2. Em contraste, a falácia do apostador assume incorretamente que a moeda agora está "na hora" para uma sequência de caudas se equilibrar.

O efeito oposto é a regressão à cauda, ​​resultante de uma distribuição com densidade de probabilidade não-evanescente em direção ao infinito

Definição para regressão linear simples de pontos de dados

Esta é a definição de regressão em direção à média que segue de perto o uso original de Sir Francis Galton .

Suponha que existam n pontos de dados { y _i , x _i }, onde i  = 1, 2, ..., n . Queremos encontrar a equação da linha de regressão , ou seja , a linha reta

${\ displaystyle y = \ alpha + \ beta x, \,}$

que forneceria um "melhor" ajuste para os pontos de dados. (Observe que uma linha reta pode não ser a curva de regressão apropriada para os pontos de dados fornecidos.) Aqui, o "melhor" será entendido como na abordagem de mínimos quadrados : uma linha que minimiza a soma dos resíduos quadrados da regressão linear modelo. Em outras palavras, os números α e β resolvem o seguinte problema de minimização:

Encontre onde${\ displaystyle \ min _ {\ alpha, \, \ beta} Q (\ alpha, \ beta)}$${\ displaystyle Q (\ alpha, \ beta) = \ sum _ {i = 1} ^ {n} {\ hat {\ varepsilon}} _ {i} ^ {\, 2} = \ sum _ {i = 1 } ^ {n} (y_ {i} - \ alpha - \ beta x_ {i}) ^ {2} \}$

Usando o cálculo , pode-se mostrar que os valores de α e β que minimizam a função objetivo Q são

${\ displaystyle {\ begin {align} & {\ hat {\ beta}} = {\ frac {\ sum _ {i = 1} ^ {n} (x_ {i} - {\ bar {x}}) ( y_ {i} - {\ bar {y}})} {\ sum _ {i = 1} ^ {n} (x_ {i} - {\ bar {x}}) ^ {2}}} = {\ frac {{\ overline {xy}} - {\ bar {x}} {\ bar {y}}} {{\ overline {x ^ {2}}} - {\ bar {x}} ^ {2}} } = {\ frac {\ operatorname {Cov} [x, y]} {\ operatorname {Var} [x]}} = r_ {xy} {\ frac {s_ {y}} {s_ {x}}}, \\ & {\ hat {\ alpha}} = {\ bar {y}} - {\ hat {\ beta}} \, {\ bar {x}}, \ end {alinhado}}}$

onde r _xy é o coeficiente de correlação amostra entre x e y , s _x é o desvio padrão de x , e s _y é, correspondentemente, o desvio padrão de y . A barra horizontal sobre uma variável significa a média da amostra dessa variável. Por exemplo:${\ displaystyle {\ overline {xy}} = {\ tfrac {1} {n}} \ textstyle \ sum _ {i = 1} ^ {n} x_ {i} y_ {i} \.}$

Substituir as expressões acima por e em resulta em valores ajustados ${\ displaystyle {\ hat {\ alpha}}}$${\ displaystyle {\ hat {\ beta}}}$${\ displaystyle y = \ alpha + \ beta x, \,}$

${\ displaystyle {\ hat {y}} = {\ hat {\ alpha}} + {\ hat {\ beta}} x, \,}$

que produz

${\ displaystyle {\ frac {{\ hat {y}} - {\ bar {y}}} {s_ {y}}} = r_ {xy} {\ frac {x - {\ bar {x}}} { s_ {x}}}}$

Isso mostra o papel que r _xy desempenha na linha de regressão de pontos de dados padronizados.

Se −1 <  r _xy  <1, então dizemos que os pontos de dados exibem regressão em direção à média. Em outras palavras, se a regressão linear é o modelo apropriado para um conjunto de pontos de dados cujo coeficiente de correlação da amostra não é perfeito, então há regressão em direção à média. O valor padronizado previsto (ou ajustado) de y está mais próximo de sua média do que o valor padronizado de x está de sua média.

Definições para distribuição bivariada com distribuições marginais idênticas

Definição restritiva

Deixe que X ₁ , X ₂ seja variáveis aleatórias com distribuições marginais idênticos com média μ . Nesta formalização, a distribuição bivariada de X ₁ e X ₂ é dita exibir regressão em direção à média se, para cada número c  >  μ , temos

μ  ≤ E [ X ₂  | X ₁  =  c ] <  c ,

com as desigualdades reversas valendo para c  <  μ .

A seguir está uma descrição informal da definição acima. Considere uma população de widgets . Cada widget tem dois números, X ₁ e X ₂ (digamos, sua extensão esquerda ( X ₁ ) e extensão direita ( X ₂ )). Suponha que as distribuições de probabilidade de X ₁ e X ₂ na população sejam idênticas e que as médias de X ₁ e X ₂ sejam μ . Agora pegamos um widget aleatório da população e denotamos seu valor X ₁ por c . (Observe que c pode ser maior, igual ou menor que μ .) Ainda não temos acesso ao valor do X ₂ deste widget . Deixe d denotar o valor esperado de X ₂ desse widget em particular. ( ou seja, deixe d denotar o valor médio de X ₂ de todos os widgets na população com X ₁ = c .) Se a seguinte condição for verdadeira:

Qualquer que seja o valor c , d está entre μ e c ( ou seja, d está mais próximo de μ do que c ),

então dizemos que X ₁ e X ₂ mostram regressão em direção à média .

Essa definição está de acordo com o uso comum atual, evoluído do uso original de Galton, do termo "regressão em direção à média". É "restritivo" no sentido de que nem toda distribuição bivariada com distribuições marginais idênticas exibe regressão em direção à média (sob esta definição).

Teorema

Se um par ( X ,  Y ) de variáveis aleatórias segue uma distribuição normal bivariável , em seguida, o E média condicional ( Y | X ) é uma função linear de X . O coeficiente de correlação r entre X e Y , junto com as médias marginais e variâncias de X e Y , determina esta relação linear:

${\ displaystyle {\ frac {E (Y \ mid X) -E [Y]} {\ sigma _ {y}}} = r {\ frac {XE [X]} {\ sigma _ {x}}}, }$

onde E [X] e E [Y] são os valores esperados de X e Y , respectivamente, e σ _x e σ _y são os desvios padrão de X e Y , respectivamente.

Por isso, o valor esperado condicional de Y , tendo em conta que X é t desvios padrão acima da sua média (e que inclui o caso em que é abaixo da sua média, quando t  <0), é rt desvios padrão acima da média de Y . Desde | r | ≤ 1, Y não está mais longe da média do que X , conforme medido no número de desvios padrão.

Portanto, se 0 ≤  r  <1, então ( X ,  Y ) mostra regressão em direção à média (por esta definição).

Definição geral

A seguinte definição de reversão em direção à média foi proposta por Samuels como uma alternativa à definição mais restritiva de regressão em direção à média acima.

Deixe que X ₁ , X ₂ seja variáveis aleatórias com distribuições marginais idênticos com média μ . Nesta formalização, a distribuição bivariada de X ₁ e X ₂ é dita exibir reversão em direção à média se, para cada número c , tivermos

μ  ≤ E [ X ₂  | X ₁  >  c ] <E [ X ₁  | X ₁  >  c ], e

μ  ≥ E [ X ₂  | X ₁  <  c ]> E [ X ₁  | X ₁  <  c ]

Essa definição é "geral" no sentido de que toda distribuição bivariada com distribuições marginais idênticas exibe reversão em direção à média .

Veja também

• Princípio de Hardy-Weinberg
• Validade interna
• Lei dos grandes números
• Martingale
• Diluição de regressão
• Viés de seleção

Referências

Leitura adicional

• JM Bland e DG Altman (junho de 1994). "Notas estatística: regressão à média" . British Medical Journal . 308 (6942): 1499. doi : 10.1136 / bmj.308.6942.1499 . PMC  2540330 . PMID  8019287 . Artigo, incluindo um diagrama dos dados originais de Galton.

• Michael R. Chernick e Robert H. Friis (2003). Bioestatística Introdutória para Ciências da Saúde . Wiley-Interscience . p. 272. ISBN 978-0-471-41137-6.

• Edward J. Dudewicz e Satya N. Mishra (1988). "Seção 14.1: Estimativa de parâmetros de regressão; Modelos lineares". Estatística Matemática Moderna . John Wiley & Sons . ISBN 978-0-471-81472-6.

• Francis Galton (1886). "Regressão à mediocridade na estatura hereditária" (PDF) . The Journal of the Anthropological Institute of Great Britain and Ireland . 15 : 246-263. doi : 10.2307 / 2841583 . JSTOR  2841583 .

• Donald F. Morrison (1967). "Capítulo 3: Amostras da população normal multivariada". Métodos estatísticos multivariados . McGraw-Hill . ISBN 978-0-534-38778-5.

• Stephen M. Stigler (1999). "Capítulo 9". Estatísticas na mesa . Harvard University Press .

• Myra L. Samuels (novembro de 1991). "Reversão estatística em direção à média: mais universal do que regressão em direção à média". The American Statistician . 45 (4): 344–346. doi : 10.2307 / 2684474 . JSTOR  2684474 .
• Stephen Senn. Regression: A New Mode for an Old Meaning , The American Statistician , Vol 44, No 2 (maio de 1990), pp. 181-183.
• David C. Schmittlein. Inferências surpreendentes de observações não surpreendentes: As expectativas condicionais realmente regressam à média? The American Statistician , Vol 43, No 3 (agosto de 1989), pp. 176–183.
• Regressão em direção à média e o estudo da mudança , Boletim Psicológico
• Uma explicação não matemática da regressão em direção à média.
• Uma simulação de regressão em direção à média.
• Amanda Wachsmuth, Leland Wilkinson, Gerard E. Dallal. Curva de Galton: uma não linearidade não descoberta nos dados de regressão da estatura da família de Galton e uma explicação provável com base nos dados de estatura de Pearson e Lee (um olhar moderno na análise de Galton.)
• Pontuações de teste padronizadas de Massachusetts, interpretadas por um estatístico como um exemplo de regressão: veja a discussão em sci.stat.edu e sua continuação .
• Gary Smith , What the Luck: The Surprising Role of Chance in Our Everyday Lives, Nova York: Overlook, Londres: Duckworth. ISBN  978-1-4683-1375-8 .

links externos

• Mídia relacionada à regressão em direção à média no Wikimedia Commons