Regra do marteloio - Rule of marteloio

A regra do marteloio é uma técnica medieval de computação de navegação que usa a direção da bússola , a distância e uma tabela trigonométrica simples conhecida como toleta de marteloio . A regra dizia aos marinheiros como traçar a travessia entre dois cursos de navegação diferentes por meio da resolução de triângulos com a ajuda do Toleta e da aritmética básica .
Aqueles que se incomodavam com a manipulação de números podiam recorrer ao visual tondo e quadro (círculo e quadrado) e obter sua resposta com divisórias . A regra do marteloio era comumente usada pelos navegadores do Mediterrâneo durante os séculos 14 e 15, antes do desenvolvimento da navegação astronômica .
Etimologia
A etimologia vem da língua veneziana . Em seu atlas de 1436, o capitão e cartógrafo veneziano Andrea Bianco introduziu uma tabela de números que chamou de toleta de marteloio ("tabela do marteloio") e o método de usá-la como raxon de marteloio ("razão do marteloio").
O significado do marteloio em si é incerto. A hipótese mais aceita, inicialmente encaminhada por AE Nordenskiöld , é que marteloio se refere a " martelo " (" martelo " em veneziano), referindo-se ao pequeno martelo que era usado para bater no sino do navio para marcar a passagem do tempo. . Foi sugerido que o sufixo - oio implica que marteloio significava não exatamente o martelo nem o martelador, mas sim "o martelar", pretendendo indicar "o martelar, o estrondo, a raquete" a partir da mudança do relógio a cada quatro horas. Como havia muitos ponteiros no convés durante a mudança de guarda, seria o momento oportuno para o piloto do navio ordenar a mudança de rumo (se necessário).
Hipóteses alternativas (não tão aceitas) são que "marteloio" é uma corruptela de mari logio (que significa "governo do mar"), ou de mare tela (que significa "rede marítima"), ou que deriva do grego homartologium ( όμαρτόλογίον , que significa "peça companheira"), ou do grego imeralogium ( ήμερόλογίον , que significa "cálculo diário") ou que pode ser do matelot do norte da França , que por sua vez vem do martolod bretão (que significa "marinheiros").
Propósito

A "regra do marteloio" foi usada na navegação europeia na Idade Média , principalmente no Mar Mediterrâneo entre os séculos 14 e 16, embora possa ter raízes mais antigas. Era parte integrante da navegação por "bússola e carta", antes do advento das coordenadas geográficas e do desenvolvimento da navegação celestial na Europa.
A navegação medieval dependia de dois parâmetros, direção e distância. A bordo do navio, a direção era determinada pela bússola do marinheiro (que surgiu por volta de 1300). A distância foi medida pelo cálculo morto , ( ou seja , distância = velocidade x tempo), onde o tempo foi medido por uma meia hora de vidro , e as leituras de velocidade foram feitas com alguma forma de um registro de chip (o método arcaico, usado no Séculos 14 e 15, envolveu o lançamento de um pedaço de madeira ou destroços ao mar; a tripulação se engajou em um canto rítmico para marcar o tempo que levou para o chip flutuar além do comprimento do navio).
Traçar um curso exigia saber a direção da bússola e a distância entre o ponto A e o ponto B. O conhecimento da localização dos portos entre si foi adquirido pelos navegadores por meio de longa experiência no mar. Essas informações às vezes eram coletadas e anotadas em um manual do piloto, conhecido como portolano ("port book", em italiano, equivalente ao grego periplus , ao roteiro do português e ao rutter do inglês ). Esses manuais foram usados para construir uma classe de mapas náuticos conhecida como cartas portulanas . As cartas Portolan começaram a ser produzidas em Gênova no final do século 13 e logo se espalharam por Veneza e Maiorca . As cartas de Portolan não eram quadriculadas por linhas de longitude e latitude, mas sim por uma teia de linhas de rumo de compasso , dando aos marinheiros uma ideia apenas da distância e direção entre os lugares.

Por um manual ou carta portulana, um navegador poderia ver imediatamente que, por exemplo, Pisa ficava 85 milhas a sudeste ("Scirocco" na nomenclatura tradicional da rosa dos ventos ) de Gênova , e assim um navio que partisse de Gênova para Pisa simplesmente mantenha esse rumo para essa distância. No entanto, a maioria dos percursos de vela não eram tão elegantes. Um marinheiro que desejasse navegar de Maiorca a Nápoles poderia dizer que este último estava para leste ("Levante") por cerca de 600 milhas - mas a ilha da Sardenha fica no caminho, portanto, o rumo do navio deve ser alterado ao longo da rota. É mais fácil falar do que fazer, pois as coordenadas geográficas não existiam nessa época. A única maneira de determinar a posição exata do navio no mar seria calcular por meio do rumo anterior e da distância percorrida.
As ilhas eram um obstáculo previsível - contornar a Sardenha seria simplesmente uma questão de navegar para sudeste por uma distância definida e, em seguida, mudar a direção para nordeste ("Greco") para o resto. Mais problemático é se o navio foi desviado de sua rota pretendida por ventos intermitentes, ou teve que se engajar em virada , mudando de rumo repetidamente. Como ele retorna ao curso pretendido? É aí que entra a regra do marteloio.
O problema transversal
A regra do marteloio abordou o problema da mudança de rumo no mar. Mais especificamente, ajudou um navegador a traçar a travessia de um curso de navegação para outro. Por exemplo, suponha que um navio navegasse da Córsega a Gênova , um curso rumo ao norte ("Tramontana") por cerca de 130 milhas. Mas os ventos não cooperam e o navio foi forçado a navegar para noroeste ("Maestro") por cerca de 70 milhas. Como ele retorna à sua rota original? Redefinir seu rumo para nordeste ("Greco") parece sensato o suficiente, mas por quanto tempo ele deve navegar nesse rumo? Como um navegador saberia quando o navio alcançou sua antiga rota e deveria virar para o norte novamente? Como evitar ultrapassar ou prejudicar o antigo curso?
Este é um problema matemático para resolver um triângulo . Se um navegador sabe quanto tempo o navio navegou no curso errado, ele pode calcular sua distância atual do curso pretendido e estimar quanto tempo ele deve navegar de volta em um novo rumo até que recupere seu curso anterior. No exemplo da Córsega para Gênova, há um triângulo ACD implícito , com um lado dado ( AC = 70 milhas no curso NW real), um ângulo de 45 ° em A (ângulo de diferença entre o curso NW real e o curso N pretendido) e outro ângulo de 90 ° a C (ângulo de diferença entre o curso real NW e o curso de retorno NE). O desafio para o navegador é descobrir quanto tempo se deve navegar no curso de retorno NE (o comprimento do CD lateral , o que é chamado de ritorno ) e quanto se avançou no curso pretendido no momento em que se endireita (o comprimento da hipotenusa AD , ou o que é chamado de avanzo total ).
Esta é a trigonometria elementar , resolvendo dois lados dados um lado (70) e dois ângulos (45 ° e 90 °). Isso é feito rapidamente aplicando a lei dos senos :
resultando nas soluções ritorno = 70 milhas e avanzo total = 98,99 milhas. Isso significa que se o navio seguir para NE a partir de sua posição atual ( C ), ele alcançará seu curso original pretendido após 70 milhas de navegação no rumo NE. No momento em que atingir seu ponto de junção ( D ), ele terá percorrido 98,99 milhas de seu curso original pretendido. Lá ele pode endireitar seu rumo N e navegar as 30 milhas restantes ou mais para Gênova.
Infelizmente, os marinheiros medievais com os níveis educacionais rudimentares dos séculos XIV e XV, provavelmente não conheciam a Lei de Sines ou a manipulavam com facilidade. Como resultado, os navegadores medievais precisavam de um método de cálculo mais simples e acessível.
Regras
"Miliária" de Ramon Llull
O erudito-clérigo Ramon Llull de Maiorca foi o primeiro escritor a referir-se a uma regra para resolver o problema transversal da navegação. Em seu Arbor Scientiae (1295), na seção de questões sobre geometria, Llul escreve:
Como os marinheiros medem milhas no mar ( miliária em mari )? Os navegantes consideram os quatro ventos gerais, ou seja, os de leste, oeste, norte e sul, e também outros quatro ventos que se encontram entre eles, grec (NE), exaloch (SE), lebeg (SW) e maestre (NW). E eles olham cuidadosamente para o centro do círculo em que os ventos (rumbos) se encontram em ângulos; eles consideram quando um navio viaja pelo vento leste ( levant ) 100 milhas do centro, quantas milhas ele faria com o vento sudeste ( exaloch ); e por 200 milhas, eles dobram o número multiplicando e então sabem quantas milhas existem do final de cada 100 milhas na direção leste ao ponto correspondente na direção sudeste. E para isso eles têm este instrumento [uma mesa matemática?] E um gráfico, canal, agulha e a estrela polar. "
O que Lúlio parece estar tentando explicar é que um navio realmente navegando a leste, mas com a intenção de navegar a sudeste, pode descobrir quanto da distância prevista para sudeste já compensou - o que os italianos chamam de " avanzar ", mas Lull parece chamar a " miliária em mari ". Lúlio não explica exatamente como, mas se refere apenas a um "instrumento", provavelmente algum tipo de mesa trigonométrica. Lull está implicando que os marinheiros podem calcular a miliária no curso pretendido multiplicando a distância realmente percorrida no curso errado pelo cosseno do ângulo entre as duas rotas.

- Miliária em mari = distância percorrida × cos ( θ )
onde θ é o ângulo de diferença entre as duas rotas.
Usando o exemplo de Lull, um navio que pretendia navegar para sudeste ("Exaloch" é catalão para "Scirocco"), mas foi forçado a navegar para o leste ("Levante"), então o ângulo de diferença é θ = 45 °. Depois de 100 milhas na rota errada, a miliária na rota pretendida é 100 × cos 45 ° = 70,71. Dobrar a navegação na rota errada para 200 milhas dobrará a miliária na rota pretendida para 141,42 milhas (= 200 cos 45 °).
(Diagramaticamente, a miliária de Lull em mari é medida pela construção de um triângulo retângulo , passando uma corda da distância percorrida no curso real até o curso pretendido, encontrando o último em um ângulo de 90 °).
Lúlio é um pouco mais explícito em seu Ars magna generalis et ultima (escrito por volta de 1305). Invertendo seu exemplo, com um navio realmente navegando para sudeste, mas pretendendo navegar para leste, Llull observa que para cada quatro milhas no rumo sudeste, ele "ganha três milhas" (2,83 na verdade) na rota pretendida para o leste. Assim, observa Lull, o navio "perde 25 milhas" (29 na verdade) de seu curso pretendido para cada 100 milhas que navega no curso atual.
Observe que em suas passagens, Ramon Lull não está recomendando a regra, mas relatando-a, insinuando que essa regra já era conhecida e usada pelos marinheiros contemporâneos na prática. Isso talvez não seja surpreendente - embora a trigonometria estivesse apenas em sua infância na Europa cristã, as tabelas de seno e cosseno já eram conhecidas na matemática árabe . O Reino de Maiorca , sob domínio muçulmano até a década de 1230, permaneceu um centro multicultural na época de Lull, com florescentes comunidades judaicas , muitas das quais se interessavam por matemática e astronomia, e cujos marinheiros tinham amplo contato com o mar Mediterrâneo. Não é improvável que os navegadores de Maiorca tivessem algum tipo de mesa trigonométrica à mão. No entanto, o conteúdo e o layout exatos dessa tabela sugeridos por Ramon Llull em 1295 são incertos.
"Toleta" de Andrea Bianco

Temos nosso primeiro vislumbre da mesa trigonométrica de um marinheiro, mais de um século depois de Lúlio. No primeiro fólio de seu atlas portulano de 1436 , o capitão veneziano Andrea Bianco explica a raxon de marteloio , como calcular a travessia e recuperar o curso. Ele prepara uma mesa trigonométrica simples que chama de toleta de marteloio e recomenda aos marinheiros que a memorizem.
A toleta de marteloio é definida da seguinte forma:
|
Quarto (ângulo de desvio) |
Alargar (distância do percurso) |
Avanzar (avanço no curso verdadeiro) |
Trimestre (ângulo de retorno) |
Ritorno (voltar ao curso) |
Avanzo di ritorno (avanço durante o retorno) |
|---|---|---|---|---|---|
| 1 | 20 | 98 | 1 | 51 | 50 |
| 2 | 38 | 92 | 2 | 26 | 24 |
| 3 | 55 | 83 | 3 | 18 | 15 |
| 4 | 71 | 71 | 4 | 14 | 10 |
| 5 | 83 | 55 | 5 | 12 | 6 1 ⁄ 2 |
| 6 | 92 | 38 | 6 | 11 | 4 |
| 7 | 98 | 20 | 7 | 10 1 ⁄ 5 | 2 1 ⁄ 5 |
| 8 | 100 | 0 | 8 | 10 | 0 |
| Para cada 100 milhas | Para cada 10 milhas alargar | ||||
Os números no Toleta podem ser aproximados pelas fórmulas modernas:
- Alargar = 100 × sin ( q × 11,15)
- Avanzar = 100 × cos ( q × 11,15)
- Ritorno = 10 / sin ( q × 11,15)
- Avanzo di ritorno = 10 / tan ( q × 11,15)
onde q = número de ventos de quarto (ângulo de diferença expresso em número de ventos de quarto). (observe que os números funcionam com um quarto de vento definido em intervalos de 11,15 °, em vez de 11,25 °, a definição usual de um quarto de vento).
O Toleta é uma tabela simples com várias colunas de números. Na primeira coluna está o ângulo de diferença entre os cursos reais e pretendidos, expresso pelo número de ventos de quarto de vento . Uma vez que essa diferença é determinada, a segunda coluna dá o Alargar (o " Widening ", a distância atual que o navio está do curso pretendido) enquanto a terceira coluna diz ao Avanzar (o "Advance", quanto da distância no pretendido o curso já foi percorrido navegando no rumo atual - isso é equivalente à miliaria di mari de Ramon Llull ). Os números de Alargar e Avanzar são mostrados na tabela de Bianco para 100 milhas de navegação no curso atual.
Exemplo : suponha que um navio pretendia navegar rumo ao leste ("Levante") do ponto A ao ponto B. Mas suponha que os ventos o obrigassem a navegar em um curso sudeste-leste (SEbE, "Quarto di Scirocco verso Levante"). Sudeste-a-leste está a três quartos dos ventos (ou 33,75 °) de leste (em uma bússola de 32 pontos , na ordem dos quartos de vento de leste, 1 quarto é leste-sul, 2 quartos é leste-sudeste , 3 quartos é sudeste-a-leste). Isso significa que o navegador deve consultar a terceira linha, q = 3, da toleta.
Suponha que o navio navegasse 100 milhas no rumo SE por E. Para verificar sua distância do curso pretendido para o leste, o marinheiro lerá a entrada correspondente na coluna alargar e verá imediatamente que ele está a 55 milhas do curso pretendido. A coluna avanzar informa que, tendo navegado 100 milhas no curso SEbE atual, ele percorreu 83 milhas do curso E pretendido.
A próxima etapa é determinar como retornar ao curso pretendido. Continuando o exemplo, para voltar ao curso pretendido para o leste, nosso marinheiro tem que reorientar o rumo do navio na direção nordeste. Mas existem vários ângulos nordeste - NbE, NNE, NE, ENE, etc. O marinheiro pode escolher o rumo - se ele retornar por um ângulo agudo (por exemplo, norte a leste), ele retornará ao curso pretendido mais rápido do que em um gradiente mais suave (por exemplo, leste a norte). Qualquer que seja o ângulo que escolher, ele deve deduzir exatamente quanto tempo deve navegar naquele rumo para alcançar seu antigo curso. Se ele navegar por muito tempo, ele corre o risco de ultrapassá-lo.
Calcular o curso de retorno é o que as últimas três colunas do toleta servem. Na quarta coluna, os ângulos de retorno são expressos como quartos do rumo do curso pretendido ( não o rumo do curso atual). Em nosso exemplo, o marinheiro pretendia ir para o leste, mas tem navegado sudeste-a-leste por 100 milhas. Dados os ventos, ele decide que é melhor retornar ao curso original reorientando o navio para leste-nordeste (ENE, "Greco-Levante"). ENE está dois quartos de vento acima do rumo pretendido , Leste, então agora ele olha para a segunda linha ("quartos = 2") na quarta coluna da tabela.
A quinta coluna é o ritorno , a distância que ele deve percorrer no ângulo de retorno escolhido para recuperar o curso original. Dado que ele escolheu retornar pelo rumo ENE (q = 2), então ele deve ler a segunda linha da coluna ritorno , que mostra o número 26. Isso representa o número necessário de milhas que ele deve viajar no rumo ENE para cada 10 milhas ele se desviou. Lembre-se, seu alargar (distância do curso pretendido) era de 55 milhas. Portanto, para retornar ao curso pretendido, ele deve viajar 5,5 × 26 = 143 milhas na ENE. Em outras palavras, ele precisa manter seu rumo ENE por 143 milhas; uma vez percorrida essa distância, ele deve endireitar seu navio para o leste e estará exatamente de volta ao curso pretendido.
A sexta e última coluna ( avanzo di ritorno ) dá a extensão do percurso pretendido que ele realizou em sua viagem de volta. Isso também é expresso em termos por 10 milhas alargar. Seu alargar era 55, e seu ângulo de retorno era ENE (portanto q = 2), o que significa que seu avanzo di ritorno é 5,5 × 24 = 132. Em outras palavras, se tudo der certo, e nosso marinheiro mantiver seu rumo ENE para 143 milhas ( ritorno ), então, durante aquele retorno, ele terá percorrido mais 132 milhas em seu curso pretendido para o leste ( avanzo di ritorno ).
Finalmente, para calcular a distância total percorrida (avanzo total) no rumo leste por toda a sua aventura, ele deve somar o avanzar durante o desvio (83 milhas) mais o avanzo di ritorno (132 milhas). Assim, no geral, ele percorreu 83 + 132 = 215 milhas no curso pretendido. Medindo essa distância no mapa a partir do ponto de partida ( A ), o navegador pode descobrir sua posição atual exata.
Este é o uso mais simples da toleta de marteloio. É, na raiz, uma tabela trigonométrica. No entanto, ela não resolve o problema transversal de uma vez, como a Lei de Sines, mas sim divide o problema em dois triângulos retângulos que passa a resolver sucessivamente. A trigonometria moderna dispensaria a etapa de cálculo do alargar e calcularia o ritorno diretamente - mas, para isso, é necessário estar armado com uma mesa sinusoidal completa . A toleta é uma mesa bastante simples, de fácil consulta e cálculos, e suficientemente compacta para ser memorizada pelos navegadores (como recomenda Bianco).
Regra de três
A toleta de marteloio é expressa por bons números redondos, 100 e 10. Mas, na prática, um navio normalmente não navegaria 100 milhas antes de tentar retornar, mas alguma outra distância, digamos 65 milhas. Calculá-lo é um problema simples de resolução de proporções . Por exemplo, se o navio navegou 65 milhas na direção sudeste-leste, então calcular o alargar do curso pretendido para o leste é simplesmente uma questão de resolver o seguinte para x :
onde 55 é o alargar para 100 milhas (conforme dado na segunda coluna da tabela em q = 3). Isso é feito facilmente pela simples " Regra de Três ", um método de multiplicação cruzada, usando três números para resolver o quarto por multiplicação e divisão sucessivas:
- x = 65 × 55 ÷ 100
Portanto, navegar por 65 milhas em SE por E implica alargar = x = 35,75 milhas. O avanzar, etc. pode ser calculado de forma análoga.
Embora a "regra de três" já fosse conhecida no século 14, a habilidade de executar a multiplicação e divisão poderia ser ilusória para os marinheiros medievais vindos de uma sociedade amplamente analfabeta. No entanto, não era inacessível. Como pedia Andrea Bianco, os navegadores devem "saber multiplicar bem e dividir bem" ("saver ben moltiplichar e ben partir"). É aqui que vemos a importante interface do comércio e da navegação. A matemática do comércio - algarismos arábicos , multiplicação, divisão, frações , as ferramentas necessárias para calcular compras e vendas de mercadorias e outras transações comerciais - era essencialmente a mesma que a matemática da navegação. E esse tipo de matemática era ensinado nas escolas de ábaco que foram estabelecidas no século 13 nos centros comerciais do norte da Itália para treinar filhos de mercadores, a mesma classe de onde os navegadores italianos eram oriundos. Como observa o historiador EGR Taylor, "os marinheiros foram o primeiro grupo profissional a usar a matemática em seu trabalho diário"
Círculo e quadrado
Para aqueles preocupados com a alta arte de manipular números, havia uma alternativa. Era o dispositivo visual conhecido como "círculo e quadrado" ( tondo e quadro ), também fornecido por Andrea Bianco em seu atlas de 1436.
O círculo era uma rosa dos ventos de 32 ventos (ou conjunto de linhas de rumo). O círculo foi inscrito com uma grade quadrada de 8 × 8.
A rosa dos ventos no centro pode ser negligenciada - na verdade, o próprio círculo pode ser ignorado, pois parece não ter outro propósito além da construção dos raios que percorrem a grade. A rosa de interesse está no canto superior esquerdo da grade quadrada. Desse canto, emana uma série de linhas de rumo do compasso . Em seu original 1436 tondo e quadro , Bianco tem dezesseis raios emanantes - isto é, Bianco inclui ventos de meio quarto, ou oitavos-ventos ( otava ), de forma que os raios emanantes estão em intervalos de 5,625 graus. Outras construções do círculo e do quadrado, por exemplo, o Cornaro Atlas , usam apenas oito raios que emanam a um quarto de vento (11,25 graus). Visualmente, esses raios replicam o quarto inferior direito de uma rosa dos ventos de 32 ventos : Leste (0q), E por S (1q), ESE (2q), SE por E (3q), SE (4q), SE por S ( 5q), SSE (6q), S por E (7q) e Sul (8q).
Acima da grade está uma escala de barra de distância , entalhada com subunidades. Existem dois conjuntos de números na escala, um para medir cada grade quadrada por 20 milhas, outro para medir cada grade quadrada por 100 milhas (veja o diagrama). A barra superior é a escala de 20 m por quadrado, com cada ponto preto denotando uma milha. A barra inferior é a escala de 100 m por quadrado, onde o comprimento de um quadrado unitário é dividido em dois sub-quadrados iguais de 50 m, e um conjunto de pontos e linhas vermelhas o divide em comprimentos de 10 milhas. Portanto, dependendo da escala escolhida, o comprimento do lado de toda a grade (oito quadrados) pode ser medido até 160 milhas (usando a escala de 20 m por quadrado) ou até 800 milhas (usando a escala de 100 m por quadrado -escala quadrada).
O querubim com as divisórias sugere como um navegador deve usar a grade para calcular alargar e avanzar por medição visual em vez de manipular números.
Exemplo : suponha que o navio tenha viajado 120 milhas com vento de um quarto abaixo do curso pretendido (por exemplo, viajou no ESE, quando o curso pretendido é Leste). Usando os divisores e a escala de 20m, o navegador pode medir 120 milhas com seus divisores. Em seguida, definindo uma extremidade no canto superior esquerdo ( A ), ele estabelece as divisórias ao longo do raio ESE (= dois quartos de vento abaixo do raio leste, ou topo horizontal da grade) e marca o ponto (ponto B no diagrama ) Em seguida, usando uma régua governante desenha uma linha até o raio Médio, e marca o correspondente ponto C .
É fácil ver imediatamente que um triângulo retângulo ABC foi criado. O comprimento BC é o alargar (distância do curso pretendido), que pode ser medido como 46 milhas (isso pode ser visto visualmente como dois quadrados de grade mais um pouco, que é 20m + 20m e um pouco que pode ser avaliado como 6m por usando as divisórias e a escala de barra de 20m). O comprimento AC é o avanzar (distância compensada ), que é 111 milhas - visualmente, cinco quadrículas e um bit, ou (20 × 5) + 11, medido por divisores e escala novamente.
É assim que o "círculo e quadrado" dispensa a manipulação de números por multiplicação e divisão ou regra de três. O navegador pode avaliar o avanzar e o alargar visualmente, apenas por medição.
Este método pode ser usado para qualquer direção e desvio pretendidos, pois o único propósito é resolver o triângulo por divisores e escala. por exemplo, usando nosso primeiro exemplo de Córsega para Gênova, onde o rumo pretendido era o norte, mas o navio realmente navegava para noroeste, o navegador ajustaria os divisores no comprimento de 70 milhas e os colocaria ao longo do vento do quarto quarto (= raio SE no tondo e quadro , já que NW está a quatro ventos de um quarto do Norte). Ele calcularia o alargar e o avanzar exatamente da mesma maneira - desenhar uma linha no topo horizontal da grade, medir os quadrados, etc.
O dispositivo tondo e quadro é muito semelhante ao quadrante sinusoidal árabe ( Rubul mujayyab ), com os raios de canto replicando o papel do fio de prumo ajustável .
Outras aplicações
Embora o toleta de marteloio (e sua contraparte visual, o tondo e quadro ) sejam projetados para a tarefa explícita de recuperar um curso pretendido, eles podem ser usados de mais maneiras, para muitas classes de problemas de navegação, por exemplo, traçando um curso com múltiplos - mudanças de suporte, etc.
Triangulação
Uma das aplicações interessantes da regra do marteloio é para a triangulação , por exemplo, determinar a distância do navio do ponto de referência da costa. (Este foi o último exercício tentado no caderno do navegador veneziano Miguel de Rodes , que reproduzimos aqui.)
Exemplo : suponha que um navio navegando para NW ("Maestro") avista um ponto de referência a oeste ("Ponente") uma noite, mas a distância é desconhecida. Suponha que o navio continue navegando na rota NW durante a noite e, na manhã seguinte, 40 milhas depois, perceba que o marco agora está na direção oeste-sudoeste (WSW, "Ponente-Libeccio") de sua posição atual. Determinar a distância do ponto de referência ao navio é apenas uma aplicação da regra do marteloio.
Para resolver o problema, comece da posição noturna ( A no mapa) e trate a distância entre o navio e o ponto de referência (comprimento AB ) como o curso pretendido e a rota real do navio (NW) como um desvio. Para calcular a distância do ponto de referência da posição do navio pela manhã ( C ) é uma questão de tratar a distância BC como o ritorno calculado. Como precisamos saber o alargar para calcular o ritorno, este é um procedimento de duas etapas.
Primeiro, observe que o NW está a quatro quartos de vento acima de W, então olhando para cima no toleta , na linha q = 4, o alargar é 71 milhas para cada 100 milhas no curso NW. Mas o navio navegou apenas 40 milhas durante a noite, então temos que resolver a razão 71/100 = x / 40, que pela regra de três significa x = alargar = 28,4 milhas. Em outras palavras, ao navegar durante a noite no NW por 40 milhas de A a C, o navio está agora a 28,4 milhas de seu curso para oeste "pretendido".
Agora, para o ritorno. O ponto de referência, conforme observado, é WSW da posição matinal do navio ( C ). Portanto, para "retornar" ao ponto de referência, o navio deve mudar seu rumo de seu rumo NW atual para um rumo WSW - ou seja, 6 quartos de vento abaixo de NW. No entanto, o toleta especifica um quarto de vento em termos de direção "pretendida" (neste caso, oeste), e WSW está dois quarto de vento abaixo do oeste, então precisamos olhar para q = 2 linha. Isso significa que o ritorno é de 26 milhas para cada 10 milhas alargar. Como o alargar é 28,4, isso significa que o ritorno é 26 × 2,84 = 73,84. E aí temos que. O marco está a 73,84 milhas de distância da posição matinal do navio.
(Para completar a história, podemos querer descobrir a distância que esse ponto de referência estava na noite anterior (ou seja, do ponto A ao ponto B). Isso é simplesmente uma questão de adicionar o avanzar e o avanzo em ritorno. Cálculos rápidos mostram o avanzar (@ q = 4, para 40 milhas) é 28,4 milhas (= 71 × 40/100) e o avanzo di ritorno (@ q = 2 para 28,4 milhas alargar), é 2,84 × 24 = 68,16. Portanto, avanzo total = 28,4 + 68,16 = 96,56 milhas. Essa foi a distância entre o ponto de referência e o navio na noite anterior.)
Encontrar locais
A regra do marteloio também pode ser usada com o avanzar como alvo, por exemplo, suponha que um navio parte com a intenção de encontrar a Linha de Tordesilhas , o meridiano legalmente estabelecido em um tratado de 1494 a 370 léguas a oeste de Cabo Verde . O navio não precisa de sair de Cabo Verde e zarpar constantemente no rumo oeste para o encontrar. Em vez disso, ele pode navegar em uma direção mais conveniente (por exemplo, SW) e tratar o oeste como um curso "pretendido". Assim, usando a regra do marteloio, ele pode navegar até que o avanzar no curso oeste "pretendido" alcance 370 léguas.
Na verdade, não precisa nem mesmo partir de Cabo Verde, mas pode partir de outro lugar, digamos, Sevilha , e usar a distância e o rumo conhecidos de Cabo Verde (viz. Sevilha) e a regra do marteloio para calcular quando finalmente atingiu o meridiano de Tordesilhas. Isso leva algumas etapas. Suponha que Cabo Verde ( B no mapa) esteja 400 léguas a sudoeste de Sevilha ( A no mapa), mas o navio pretende ir direto para oeste de Sevilha para alcançar o meridiano de Tordesilhas em mar aberto. Quanto tempo precisa para navegar?

A maneira de resolver isso pela regra do marteloio é colocar o problema ao contrário: trate Oeste como rumo pretendido e SW como curso real. SW está quatro quarto de vento abaixo de W, então olhando para cima no toleta para q = 4, o avanzar é 71 para cada 100 milhas navegadas. Assim, se um navio navegasse 400 léguas no curso "real" de SW para Cabo Verde, alcançaria uma avanzar de 284 léguas (= 71 × 4) no curso "pretendido" para Oeste. Claro, o navio não está realmente navegando a sudoeste para Cabo Verde, mas navegando ao oeste em mar aberto. Por outras palavras, quando o navio sai de Sevilha para oeste, sabe que precisa de navegar 284 léguas a oeste antes de atingir o meridiano implícito de Cabo Verde (ponto C no mapa), e só deve começar a contar as 370 léguas até ao Linha de Tordesilhas depois disso. Em outras palavras, ele precisa navegar um total de 284 + 370 = 654 léguas a oeste de Sevilha para chegar à linha de Tordesilhas (ponto D no mapa).
Embora este exemplo em particular mostre a flexibilidade da regra do marteloio, ele também mostra uma de suas principais desvantagens: o resultado ignora completamente a curvatura da Terra , ou seja, o fato de que os meridianos de longitude convergem para o Pólo Norte e, portanto, se estreitam em latitudes mais altas. Ao contrário do que o marteloio sugere, 370 léguas a oeste de Cabo Verde não está no mesmo meridiano de longitude que 654 léguas a oeste de Sevilha. Como Sevilha fica bem ao norte de Cabo Verde, os meridianos estão agrupados mais próximos na latitude de Sevilha do que na latitude de Cabo Verde. Um navio que navegue a oeste de Sevilha chegará, de fato, ao meridiano real de Tordesilhas (ponto T no mapa) bem antes do início de 654 léguas (ponto D ).
A regra do marteloio manda os marinheiros traçarem as rotas desenhando triângulos planos em um mapa, como se a superfície do mundo fosse plana. Embora isso possa ser prático o suficiente para navegar confinado às latitudes compactas do Mar Mediterrâneo , é bastante enganoso em uma escala maior.
Relação com regras posteriores
Relação com o "regimento das ligas"
No final dos séculos 15 e 16, o aprimoramento da astronomia náutica e a introdução de paralelos de latitude permitiram aos navegadores determinar sua posição no mar por leituras celestes, em vez de depender da estimativa da distância percorrida. O sucessor do Estado de marteloio foi o "regimento das Ligas" ( regimento das léguas ), que foi usado por vela navegadores Português no Oceano Atlântico. Ou, para usar o termo introduzido por William Bourne (1571), a "Regra para Elevar ou Estabelecer um Grau", também conhecida como "Tabela das Ligas" ou "Regra para Elevar o Pólo". Foi inicialmente escrito no manual de navegação português Regimento do astrolabio e do quadrante (publicado em Lisboa por volta de 1509, mas escrito por volta de 1480). Foi popularizado por Martín Cortés de Albacar no seu compendio Breve la esfera e del arte de navegar de 1551 .
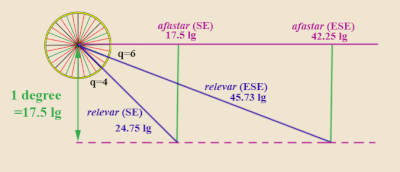
O “Regimento das Ligas” não difere muito da regra do marteloio. O Regimento das Ligas sempre considera o rumo oeste-leste como o "curso pretendido" e as medidas estabelecem desvios dele. Mais especificamente, a tabela classificativa considera um valor fixo de alargar - fixado em 1 grau de latitude (ou, nas medidas do tempo, 17,5 ligas (portuguesas) , ou o equivalente a 70 milhas (italianas) ). Ele então fornece para cada vento de quarto diferente da direção de navegação (sempre designado como quartos de distância do eixo norte-sul, ao invés de longe do curso pretendido), o relevar e o afastar . O relevar é o número de léguas no curso real que um navio deve navegar para cobrir o 1 grau de latitude predefinido (17,5 léguas de alargar a partir do paralelo de partida). O afastar é apenas o avanzar correspondente na direção oeste-leste.
Exemplo : suponha que um navio parte em direção leste-sudeste (ESE). Ou seja, seis quartos de vento acima do Sul (lembre-se: ao contrário do marteloio, o Regimento das Ligas sempre mede um quarto de vento do meridiano norte-sul). Olhando para qualquer regimento da tabela de ligas (por exemplo, Martín Cortés de Albacar , 1551), para q = 6, a tabela dá o relevar como 45 11 ⁄ 15 ligas e o afastar como 42 1 ⁄ 4 ligas. Isso significa que um navio navegando no rumo ESE terá que navegar 45,73 léguas para cobrir um grau de latitude (17,5 léguas de alargar do rumo leste, para usar a língua marteloio), e o correspondente afastar ( avanzar em termos de marteloio) ser 42,25 ligas.
Se, em vez disso, o navio partiu em um rumo SE, ou seja, quatro quartos de vento acima do Sul, os valores correspondentes da tabela do Regimento das Ligas em q = 4 são relevar = 24 3 ⁄ 4 e o afastar = 17 1 ⁄ 2 .
Observe que o rumo SE atinge 1 grau alargar mais rápido (ou seja, menor relevar ) do que o rumo ESE, e terá menos afastar (mais perto do meridiano N – S).
Matematicamente,
- relevar = 17,5 / cos θ
- afastar = 17,5 × tan θ
onde θ = 11,25 × número de quartos de vento longe do eixo norte-sul.
Apesar da diferença de terminologia, notadamente no uso de graus de latitude, a regra do marteloio e o Regimento das Ligas são muito semelhantes - ambos tratam da resolução de triângulos em um mapa plano. A vantagem do regimento sobre o marteloio é a introdução de paralelos de latitude na tabela, de forma que a posição possa ser verificada por observação astronômica (via quadrante , astrolábio , etc.), e não tenha que depender totalmente de estimativas de distância e direção.
Com o regimento, as coordenadas geográficas também podem ser usadas para orientar a navegação. Por exemplo, a busca pela linha de Todesilhas (meridiano 370 léguas a oeste de Cabo Verde) é muito simplificada por referência a uma latitude precisa. Por exemplo, suponha que dois navios partam de Cabo Verde (17 ° N), um em um rumo oeste por norte (WbN, que é um quarto acima de oeste, ou q = 7 do eixo norte), o outro por um rumo oeste-noroeste (WNW, dois quartos acima do oeste, ou q = 6 do eixo Norte). Usando o Regimento das Ligas, é possível calcular as latitudes precisas quando irão cruzar o meridiano de Tordesilhas - basta dividir 370 léguas a oeste pelo afastar implícito nas diferentes direções. O navio WbN alcançará o meridiano quando atingir a latitude 21 ° 21 'N, enquanto o navio WNW irá alcançá-lo quando atingir a latitude 29 ° N. Assim, em vez de contar léguas com ampulheta e leituras de velocidade, os navios podem apenas manter o rumo, e fazer observações astronômicas periódicas para avaliar sua latitude.
Relação com "navegação transversal"
A toleta de marteloio é ancestral da moderna " mesa transversal " usada na navegação mais moderna. Na nomenclatura moderna, a travessia é o "caminho tortuoso feito por um navio quando ele navega em várias direções sucessivas" e resolver a travessia é "o método de encontrar um único curso e distância que levaria um navio ao mesmo lugar que dois ou mais cursos e distâncias ". Na língua marteloio, ao "resolver a travessia", as informações conhecidas dadas são o "curso real" e o "ritorno", enquanto as incógnitas são o "rumo pretendido" e o "avanzo total".
As tabelas transversais usam três valores para cada um dos segmentos tortuosos do curso - a distância (Dist.), A diferença de latitude (D.Lat., Movimento ao longo do eixo N – S) e a partida (Dep., Movimento ao longo do eixo E – W) , os dois últimos calculados pelas fórmulas:
- Diferença de latitude = distância × cos θ
- Partida = distância × sen θ
onde θ é a diferença angular do curso do eixo N – S se os valores de θ forem menores que 45 °; se, no entanto, o ângulo exceder 45 °, então θ é expresso como o ângulo de diferença do eixo E – W, e as fórmulas são invertidas, ou seja, a fórmula de diferença de latitude torna-se a partida, e a fórmula de partida é a diferença de Latitude). Ou, ainda mais simplesmente, calcule θ como o ângulo de diferença do vento principal mais próximo (N, S, E, W), execute as fórmulas e coloque o número maior na coluna apropriada (D.Lat. Ou Dep.) .
Para cada segmento de curso, o navegador insere o trio relevante (Dist., D.Lat., Dep.) E pode calcular o rumo implícito do início ao ponto final e a distância compensada nesse rumo. Ele então combina, por adição e subtração, todas as diferenças de latitude e partida, para obter a diferença geral de latitude e partida, e a converte de volta em direção e distância totais compensadas.
Fontes de manuscritos
Deixando de lado as sugestões de Ramon Llull em 1295, a referência mais antiga conhecida ao marteloio é datada de 1390, no inventário da propriedade da mãe de um certo Oberto Foglieto de Gênova, onde se lê unum martelogium .... item carta una pro navegando . A primeira aparição e explicação claras é o atlas de 1436 do capitão veneziano Andrea Bianco . Outros manuscritos antigos já foram encontrados relacionando a regra do marteloio, incluem:

- um códice veneziano anônimo do século 15, pós-1428, que já foi parte da coleção do Doge Marco Foscarini , agora perdido.
- o Liber do marinheiro veneziano Miguel de Rodes (c. 1434-36) (Sra. em coleção particular)
- o portolano do Adriático de Grazioso Benincasa de Ancona, compilado de 1435 a 1445 (Sra. na Biblioteca comunale Luciano Benincasa em Ancona , Itália).
- o manuscrito portolano veneziano Alcune raxion de marineri de Pietro di Versi , c. 1444 (Ms.It.IV. 170 na Biblioteca Nazionale Marciana em Veneza , Itália)
- O Livro do trompetista naval veneziano conhecido como Zorzi Trombetta de Modone, datado de c. 1444–1449 (Cotton MS. Titus A.XXVI na British Library em Londres, Reino Unido)
- Manuscrito veneziano anônimo conhecido como Arte Veneziana del Navigare , c. 1444–1445 (Sra. CM17 na Biblioteca del Museo Civico de Padova em Pádua , Itália).
- Ragioni antique spettanti dall'arte del mare et fabriche de vasselli (Ms. NVT 19, no National Maritime Museum em Greenwich, Reino Unido).
- Cornaro Atlas , a c. Cópia de 1489 de um manuscrito anterior, (Ms.Egerton 73 na Biblioteca Britânica em Londres)
- Portolano veneziano anônimo do século 15 (Sra. 3345 * (Fosc.307) no Österreichische Nationalbibliothek (ÖNB) em Viena , Áustria)
Notas
Fontes externas
- Altante Bianco, 1436 em Internetculturale.it; Resolução mais alta em Geoweb.sbn.venezia.it.
- McGee, D. et al. (2003 em diante) Michael de Rodes: Um marinheiro medieval e seu website manuscrito (acessado em 20 de julho de 2011). (originalmente hospedado pelo Instituto Dibner de História da Ciência e Tecnologia no MIT , agora hospedado pelo Instituto Museo Galileo e Museu da História da Ciência em Florença, Itália)
Referências
- Aczel, AD (2001) The Riddle of the Compass: a invenção que mudou o mundo New York: Harcourt.
- Albertis, EA (1893) Le construzioni navale e l'arte della navigazione al tempo di Cristoforo Colombo , Pat IV, vol. 1 de Raccolta di Documenti e Studi Pubblicati dalla Reale Commissione Colombiana pel quarto Centenario della scoperta dell'America . Roma: Ministero della Pubblica Istruzione.
- Albuquerque, L. de (1970) "A navegação astronômica", in A. Cortesão, editor, 1969–70, História da cartografia portuguesa , vol. 2. Lisboa: Junta de Investigações do Ultramar, p. (reimpresso em 1975, Estudos de História , Vol. 3. Coimbra: UC Biblioteca Geral online )
- Albuquerque, Luís de (1973) "O Tratado de Tordesilhas e as dificuldades técnicas da sua aplicação rigorosa" in El Tratado de Tordesillas y su Proyeccion , vol. 1, pp. 119–366. (Reimpresso em 1974, Estudos de História , Vol. 2. Coimbra: UC Biblioteca Geral. Pp. 221p56
- Breusing, A. (1881) "La toleta de Martelojo und die loxodromischen Karten", Zeitschrift für wissenschaftliche Geographie , vol. II, Pt. 1 ( pp. 129–33 ), Pt.2 ( pp. 180–95 ).
- Brummelen, G. (2010) "Clear Sailing with Trigonometry" em D. Jardine e A. Shell-Gellasch , editores, Mathematical Time Capsules: Historical modules for the mathematics classroom . Mathematical Association of America.
- Campbell, T. (1987) "Cartas Portolan do final do século XIII a 1500", em JB Harley e D. Woodward, editores, The History of Cartography, Vol. 1 - Cartografia na Europa Pré-histórica, Antiga e Medieval e no Mediterrâneo . Chicago: University of Chicago Press, pp. 371-63 online (PDF)
- Cortesão, A. (1969) História da Cartografia Portuguesa . Coimbra: Junta de Investigações do Ultramar
- Cotter, CH (1978) "Early tabular, graphic and instrumental, methods for solving problems of plane sailing", Revista da Universidade de Coimbra , Vol. 26, pp. 3-20 offprint
- D'Avezac, MAP Marquis (1874) Aperçus historiques sur la rose des vents: lettre à Monsieur Henri Narducci . Roma: Civelli online
- Desimoni, C. (1888) "Le carte nautiche italiane del Medio Evo, a proposito di un libro del prof. Fischer", Atti della Società ligure di storia patria , vol. 19, pp. 225–66.
- Diffie, Bailey W. e George D. Winius (1977) Foundations of the Portuguese impire, 1415–1580 Minneapolis, MN: University of Minnesota Press.
- Edson, E. (2007) The World Map, 1300–1492: a persistência da tradição e transformação . Baltimore, MD: The Johns Hopkins University Press.
- Formaleoni, Vicenzio (1783) Saggio sulla Nautica antica de 'Veneziani, com uma ilustração de alcuna carte idrografiche antiché da Biblioteca de S. Marco, que dimonstrano l'isole Antille prima della scoperta di Cristoforo Colombo . Veneza. conectados
- Gelcich, E. (1892) "I primi passi della scienza nautica", Rivista Marittima , Vol. 25, pp. 71-102
- Kelley, JE (2000) Navegação analógica e digital no final da Idade Média , Melrose Park, Pa .: Someime Publishers
- Kelley, JE (1995) "Perspectives on the Origins and Use of Portolan Charts", Cartographica , vol. 32 (3), pp. 1-16. conectados
- Kretschmer, K. (1909) Die italienischen Portolane des Mittelalters: Ein Beitrag zur Geschichte der Kartographie und Nautik . Berlim: Mittler und Sohn
- Long, PI, D. McGee e AM Stahl, editores, (2009) O Livro de Michael de Rodes: Um manuscrito do século XV . 3 volumes, Cambridge, Mass: MIT Press.
- Masiero, F. (1984) "La raxon de marteloio", Studi veneziani , vol. 8, pp. 393–412.
- Merrifield, J. (1883) Treatise on Navigation . Londres: Spottiswoode. conectados
- Morelli, Jacopo (1810) Lettera rarissima di Cristoforo Colombo . Bassano: Stamperia Remondiniana online
- Nordenskiöld, Adolf Erik (1897) Periplus: An Essay on the Early History of Charts and Sailing Directions , tr. Frances A. Bather, Estocolmo: Norstedt.
- Parry, JH (1974) The Discovery of the Sea , edição de 1984, Berkeley: University of California Press. conectados
- Ramon Llull (1305) Ars magna generalis et ultima , edição de 1517, online , esp. Parte 10, "De Navigatione", fo. 93, p.213
- Ramon Llull (1295) L'arbre de ciència , 1635 Ed latim: Arbor scientiæ venerabilis et cælitvs illuminati patris Ravmvndi Lvllii Maiorieensis Lyons: Pillehotte. conectados
- Randles, WGL "(1998) The Emergence of Nautical Astronomy in Portugal in the XVth Century", Journal of Navigation , vol. 51, pp. 46–57.
- Rossi, F. (2009) "Introdução" ao Volume 2 de Long, McGee e Stalh, editores, Livro de Michael de Rodes . ( online )
- Ruge, S. (1900) "Der Periplus Nordenskiölds", Deutsche geographische Blätter Vol. 23, No. 4, pp. 161-228
- Sezgin, F. (2007) Geografia Matemática e Cartografia no Islã e sua continuação no Ocidente . Instituto de História da Ciência Árabe-Islâmica
- Taylor, EGR (1950) "Five Centuries of Dead Reckoning", Journal of Navigation , Vol. 3, pp. 280–85.
- Taylor, EGR (1956) The Haven-Finding Art: A history of navigation from Odysseus to Captain Cook , 1971 ed., London: Hollis and Carter.
- Taylor, EGR (1960) "Matemática e o Navegador no Século XIII", Journal of Navigation , Vol. 13, pp. 1-12.
- Toaldo, Giuseppe (1782) "Lettera a sua Eccellenza il. Sig. Cav. Giacopo Nani, conteúdo la spiegazione d'un antica Regola di navigare Practicata da 'Veneziani , Saggi di studi Veneti Veneza: Storti. Pp. 40-61
- Vernet, J. (2008) "O Mundo Científico da Coroa de Aragão sob Jaime I" em Ramon Llull e o Islã, o início do diálogo . Barcelona: IEMed., Pp. 99-114.
- Waters, DW (1988) "Reflexões sobre alguns problemas de navegação e hidrografia do século XVI relacionados com a viagem de Bartolomeu Dias", Revista da Universidade de Coimbra , vol. 34, pp. 275 347. separata