Coordenadas de nascimento - Born coordinates

Geometria espaço-temporal das coordenadas de Born. As linhas vermelhas ( | ) são linhas mundiais (congruência) de pontos no disco (com r = z = ϕ = const.). As listras azuis e cinza entrelaçadas mostram a mudança de t (listras de simultaneidade). As curvas laranja ( / \ ) são curvas semelhantes à luz (geodésicas nulas) com r fixo .

Na física relativística , o gráfico de coordenadas de Born é um gráfico de coordenadas para (parte do) espaço-tempo de Minkowski , o espaço-tempo plano da relatividade especial . É freqüentemente usado para analisar a experiência física de observadores que andam em um anel ou disco girando rigidamente em velocidades relativísticas , os chamados observadores de Langevin . Este gráfico é frequentemente atribuído a Max Born , devido ao seu trabalho de 1909 sobre a física relativística de um corpo em rotação. Para uma visão geral da aplicação de acelerações no espaço-tempo plano, consulte Aceleração (relatividade especial) e referencial adequado (espaço-tempo plano) .

Com base na experiência de cenários inerciais (ou seja, medições em referenciais inerciais), os observadores Langevin sincronizam seus relógios pela convenção de Einstein padrão ou por sincronização lenta do relógio , respectivamente (ambas as sincronizações internas). Para um certo observador Langevin, este método funciona perfeitamente. Em sua vizinhança imediata, os relógios são sincronizados e a luz se propaga isotrópica no espaço. Mas a experiência quando os observadores tentam sincronizar seus relógios ao longo de um caminho fechado no espaço é intrigante: sempre há pelo menos dois relógios vizinhos com horários diferentes. Para remediar a situação, os observadores concordam com um procedimento de sincronização externa (tempo de coordenada t - ou para observadores em anel, um tempo de coordenada adequado para um raio fixo r ). Por este acordo, os observadores Langevin montados em um disco girando rigidamente concluirão, a partir de medições de pequenas distâncias entre si, que a geometria do disco é não euclidiana. Independentemente de qual método eles usem, eles concluirão que a geometria é bem aproximada por uma certa métrica Riemanniana , ou seja, a métrica Langevin-Landau-Lifschitz. Isso, por sua vez, é muito bem aproximado pela geometria do plano hiperbólico (com as curvaturas negativas -3  ω ² e -3  ω ²  r ² , respectivamente). Mas se esses observadores medirem distâncias maiores, eles obterão resultados diferentes , dependendo do método de medição que usarem! Em todos esses casos, entretanto, eles provavelmente obterão resultados inconsistentes com qualquer métrica Riemanniana . Em particular, se eles usarem a noção mais simples de distância, distância de radar, devido a vários efeitos como a assimetria já observada, eles concluirão que a "geometria" do disco não é apenas não euclidiana, é não riemanniana.

O disco giratório não é um paradoxo . Qualquer que seja o método que os observadores utilizem para analisar a situação: no final, eles se veem analisando um disco giratório e não um referencial inercial.

Observadores Langevin no gráfico cilíndrico

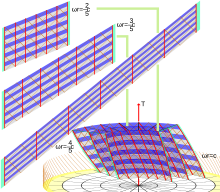
Para motivar o gráfico de Born, primeiro consideramos a família de observadores Langevin representados em um gráfico de coordenadas cilíndricas comum para o espaço-tempo de Minkowski. As linhas de mundo desses observadores formam uma congruência temporal que é rígida no sentido de ter um tensor de expansão desaparecendo. Eles representam observadores que giram rigidamente em torno de um eixo de simetria cilíndrica.

Fig. 1: Parte da linha helicoidal mundial de um observador Langevin típico (curva vermelha), representada no gráfico cilíndrico, com alguns cones de luz futuros apontando (ouro) com os vetores de moldura atribuídos pela moldura Langevin (hastes pretas). Nesta figura, a coordenada Z não é essencial e foi suprimida. O cilindro branco mostra um lugar geométrico de raio constante; a linha verde tracejada representa o eixo de simetria R = 0. A curva azul é uma curva integral do vetor de unidade azimutal .${\ displaystyle {\ vec {p}} _ {3}}$

Do elemento de linha

${\ displaystyle {\ begin {alinhados} & \ mathrm {d} s ^ {2} = - \ mathrm {d} T ^ {2} + \ mathrm {d} Z ^ {2} + \ mathrm {d} R ^ {2} + R ^ {2} \, \ mathrm {d} \ Phi ^ {2}, \; \; \\ & - \ infty <T, \, Z <\ infty, \; 0 <R < \ infty, \; - \ pi <\ Phi <\ pi \ end {alinhado}}}$

podemos ler imediatamente um campo de quadro que representa os quadros Lorentz locais de observadores estacionários (inerciais)

${\ displaystyle {\ vec {e}} _ {0} = \ parcial _ {T}, \; \; {\ vec {e}} _ {1} = \ parcial _ {Z}, \; \; { \ vec {e}} _ {2} = \ parcial _ {R}, \; \; {\ vec {e}} _ {3} = {\ frac {1} {R}} \, \ parcial _ { \ Phi}}$

Aqui, é um campo vetorial unitário semelhante ao tempo , enquanto os outros são campos vetoriais unitários semelhantes ao espaço ; em cada evento, todos os quatro são mutuamente ortogonais e determinam o quadro de Lorentz infinitesimal do observador estático cuja linha de mundo passa por aquele evento. ${\ displaystyle {\ vec {e}} _ {0}}$

Aumentando simultaneamente esses campos de quadro na direção, obtemos o campo de quadro desejado que descreve a experiência física dos observadores de Langevin, a saber ${\ displaystyle {\ vec {e}} _ {3}}$

${\ displaystyle {\ vec {p}} _ {0} = {\ frac {1} {\ sqrt {1- \ omega ^ {2} \, R ^ {2}}}} \, \ parcial _ {T } + {\ frac {\ omega \, R} {\ sqrt {1- \ omega ^ {2} \, R ^ {2}}}} \; {\ frac {1} {R}} \ parcial _ { \ Phi}}$

${\ displaystyle {\ vec {p}} _ {1} = \ parcial _ {Z}, \; \; {\ vec {p}} _ {2} = \ parcial _ {R}}$

${\ displaystyle {\ vec {p}} _ {3} = {\ frac {1} {\ sqrt {1- \ omega ^ {2} \, R ^ {2}}}} \; {\ frac {1 } {R}} \, \ partial _ {\ Phi} + {\ frac {\ omega \, R} {\ sqrt {1- \ omega ^ {2} \, R ^ {2}}}} \, \ parcial _ {T}}$

Aparentemente, esse quadro foi introduzido pela primeira vez (implicitamente) por Paul Langevin em 1935; seu primeiro uso explícito parece ter sido por TA Weber, ainda em 1997! É definido na região 0 <R <1 / ω; esta limitação é fundamental, uma vez que próximo ao limite externo, a velocidade dos observadores Langevin se aproxima da velocidade da luz.

Fig. 2: Esta figura mostra as linhas de mundo de um observador fiducial Langevin (curva vermelha) e seus vizinhos mais próximos (curvas azuis marinho tracejadas). Mostra um quarto de uma órbita pelo observador fiducial em torno do eixo de simetria (linha verde vertical).

Cada curva integral do campo vetorial de unidade semelhante ao tempo aparece no gráfico cilíndrico como uma hélice com raio constante (como a curva vermelha na Fig. 1). Suponha que escolhemos um observador Langevin e consideramos os outros observadores que andam em um anel de raio R que está girando rigidamente com velocidade angular ω. Então, se tomarmos uma curva integral (curva helicoidal azul na Fig. 1) do vetor de base espacial , obteremos uma curva que podemos esperar que possa ser interpretada como uma "linha de simultaneidade" para os observadores em anel. Mas, como vemos na Fig. 1, os relógios ideais carregados por esses observadores em anel não podem ser sincronizados . Esta é nossa primeira sugestão de que não é tão fácil como se poderia esperar definir uma noção satisfatória de geometria espacial mesmo para um anel giratório , muito menos um disco giratório!${\ displaystyle {\ vec {p}} _ {0}}$${\ displaystyle {\ vec {p}} _ {3}}$

Calculando a decomposição cinemática da congruência de Langevin, descobrimos que o vetor de aceleração é

${\ displaystyle \ nabla _ {{\ vec {p}} _ {0}} {\ vec {p}} _ {0} = {\ frac {- \ omega ^ {2} \, R} {1- \ ômega ^ {2} \, R ^ {2}}} \; {\ vec {p}} _ {2}}$

Isso aponta radialmente para dentro e depende apenas do raio (constante) de cada linha mundial helicoidal. O tensor de expansão desaparece de forma idêntica, o que significa que os observadores Langevin próximos mantêm uma distância constante uns dos outros. O vetor de vorticidade é

${\ displaystyle {\ vec {\ Omega}} = {\ frac {\ omega} {1- \ omega ^ {2} \, R ^ {2}}} \; {\ vec {p}} _ {1} }$

que é paralelo ao eixo de simetria. Isso significa que as linhas de mundo dos vizinhos mais próximos de cada observador Langevin estão se torcendo em torno de sua própria linha de mundo , como sugerido pela Fig. 2. Esse é um tipo de noção local de "redemoinho" ou vorticidade.

Em contraste, observe que projetar as hélices em qualquer um dos hiperslices espaciais ortogonais às linhas de mundo dos observadores estáticos resulta em um círculo, que é obviamente uma curva fechada. Melhor ainda, o vetor de base coordenada é um campo vetorial Killing semelhante a um espaço cujas curvas integrais são curvas semelhantes a espaços fechadas (círculos, na verdade), que além disso degeneram em curvas fechadas de comprimento zero no eixo R = 0. Isso expressa o fato de que nosso espaço-tempo exibe simetria cilíndrica e também exibe uma espécie de noção global da rotação de nossos observadores Langevin. ${\ displaystyle T = T_ {0}}$${\ displaystyle \ partial _ {\ Phi}}$

Na Fig. 2, a curva magenta mostra como os vetores espaciais estão girando (o que é suprimido na figura, uma vez que a coordenada Z não é essencial). Ou seja, os vetores não são transportados por Fermi-Walker ao longo da linha do mundo, então o referencial Langevin está girando , bem como não inercial . Em outras palavras, em nossa derivação direta do quadro de Langevin, mantivemos o quadro alinhado com o vetor de base das coordenadas radiais . Ao introduzir uma rotação de taxa constante do quadro transportado por cada observador Langevin , poderíamos, se quiséssemos "despin" nosso quadro para obter uma versão girostabilizada. ${\ displaystyle {\ vec {p}} _ {2}, \; {\ vec {p}} _ {3}}$${\ displaystyle {\ vec {p}} _ {1}}$${\ displaystyle {\ vec {p}} _ {2}, \; {\ vec {p}} _ {3}}$${\ displaystyle \ partial _ {R}}$${\ displaystyle {\ vec {p}} _ {1}}$

Transformando-se no mapa de Born

Fig. 3: Uma tentativa de definir uma noção de "espaço por vez" para nossos observadores Langevin, representada no mapa de Born. Essa tentativa está fadada ao fracasso por pelo menos duas razões! Esta figura representa a região 0 < r <1 quando ω = 1/5, com uma descontinuidade em ϕ = π. O raio radial a partir do qual "desenvolvemos" as curvas integrais para fazer a superfície está em ϕ = 0 (no lado oposto nesta imagem).

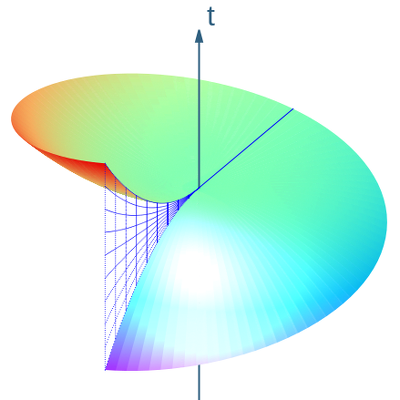
Para obter o gráfico de Born , endireitamos as linhas helicoidais do mundo dos observadores Langevin usando a transformação de coordenadas simples

${\ displaystyle t = T, \; \; z = Z, \; \; r = R, \; \; \ phi = \ Phi - \ omega \, T}$

O novo elemento de linha é

${\ displaystyle \ mathrm {d} s ^ {2} = - \ left (1- \ omega ^ {2} r ^ {2} \ right) \ mathrm {d} t ^ {2} +2 \ omega r ^ {2} \ mathrm {d} t \, \ mathrm {d} \ phi + \ mathrm {d} z ^ {2} + \ mathrm {d} r ^ {2} + r ^ {2} \ mathrm {d } \ phi ^ {2},}$

${\ displaystyle - \ infty <t, \, z <\ infty, 0 <r <{\ frac {1} {\ omega}}, \; - \ pi <\ phi <\ pi}$

Observe os "termos cruzados" envolvendo , que mostram que o gráfico de Born não é um gráfico de coordenadas ortogonais . As coordenadas de Born às vezes também são chamadas de coordenadas cilíndricas rotativas . ${\ displaystyle \ mathrm {d} t \, \ mathrm {d} \ phi}$

No novo gráfico, as linhas de mundo dos observadores Langevin aparecem como linhas retas verticais. Na verdade, podemos transformar facilmente os quatro campos vetoriais que constituem o quadro de Langevin no novo gráfico. Nós obtemos

${\ displaystyle {\ vec {p}} _ {0} = {\ frac {1} {\ sqrt {1- \ omega ^ {2} \, r ^ {2}}}} \, \ parcial _ {t }}$

${\ displaystyle {\ vec {p}} _ {1} = \ parcial _ {z}, \; \; {\ vec {p}} _ {2} = \ parcial _ {r}}$

${\ displaystyle {\ vec {p}} _ {3} = {\ frac {\ sqrt {1- \ omega ^ {2} \, r ^ {2}}} {r}} \, \ parcial _ {\ phi} + {\ frac {\ omega \, r} {\ sqrt {1- \ omega ^ {2} \, r ^ {2}}}} \, \ parcial _ {t}}$

Esses são exatamente os mesmos campos vetoriais de antes - agora eles são simplesmente representados em um gráfico de coordenadas diferente!

Desnecessário dizer que, no processo de "desenrolar" as linhas de mundo dos observadores Langevin, que aparecem como hélices no gráfico cilíndrico, "enrolamos" as linhas de mundo dos observadores estáticos, que agora aparecem como hélices no gráfico de Born ! Observe também que, como o quadro de Langevin, o gráfico de Born só é definido na região 0 <r <1 / ω.

Se recalcularmos a decomposição cinemática dos observadores Langevin, ou seja, da congruência temporal , obteremos com certeza a mesma resposta que obtivemos antes, apenas expressa em termos do novo gráfico. Especificamente, o vetor de aceleração é ${\ displaystyle {\ vec {p}} _ {0} = {\ frac {1} {\ sqrt {1- \ omega ^ {2} \, r ^ {2}}}} \, \ parcial _ {t }}$

${\ displaystyle \ nabla _ {{\ vec {p}} _ {0}} \, {\ vec {p}} _ {0} = {\ frac {- \ omega ^ {2} \, r} {1 - \ omega ^ {2} \, r ^ {2}}} \, {\ vec {p}} _ {2}}$

o tensor de expansão desaparece, e o vetor de vorticidade é

${\ displaystyle {\ vec {\ Omega}} = {\ frac {\ omega} {1- \ omega ^ {2} \, r ^ {2}}} \; {\ vec {p}} _ {1} }$

O campo covetor duplo do campo vetorial unitário semelhante ao tempo em qualquer campo de quadro representa hiperslices espaciais infinitesimais. No entanto, o teorema da integrabilidade de Frobenius dá uma forte restrição sobre se esses elementos do hiperplano espacial podem ou não ser "entrelaçados" para formar uma família de hipersuperfícies espaciais que são ortogonais em todos os lugares às linhas de mundo da congruência. Na verdade, isso é possível, caso em que dizemos que a congruência é ortogonal de hipersuperfície , se e somente se o vetor de vorticidade desaparecer de forma idêntica . Assim, enquanto os observadores estáticos no gráfico cilíndrico admitem uma única família de hiperslices ortogonais , os observadores de Langevin não admitem tais hiperslices . Em particular, as superfícies espaciais no gráfico de Born são ortogonais aos observadores estáticos, não aos observadores Langevin . Esta é nossa segunda (e muito mais pontual) indicação de que definir "a geometria espacial de um disco giratório" não é tão simples quanto se poderia esperar. ${\ displaystyle T = T_ {0}}$${\ displaystyle t = t_ {0}}$

Para entender melhor este ponto crucial, considere as curvas integrais do terceiro vetor de quadro de Langevin

${\ displaystyle {\ vec {p}} _ {3} = {\ sqrt {1- \ omega ^ {2} \, r ^ {2}}} \, {\ frac {1} {r}} \, \ parcial _ {\ phi} + {\ frac {\ omega \, r} {\ sqrt {1- \ omega ^ {2} \, r ^ {2}}}} \, \ parcial _ {t}}$

que passam pelo raio . (Por conveniência, suprimiremos a coordenada não essencial z de nossa discussão.) Essas curvas estão na superfície ${\ displaystyle \ phi = 0, \, t = 0}$

${\ displaystyle \ phi + \ omega \, t - {\ frac {t} {\ omega \, r ^ {2}}} = 0, \; \; - \ pi <\ phi <\ pi}$

mostrado na Fig. 3. Gostaríamos de considerar isso como um "espaço por vez" para nossos observadores Langevin. Mas duas coisas dão errado.

Primeiro, o teorema de Frobenius nos diz que não são tangentes a nenhum hiperslice espacial. Na verdade, exceto no raio inicial, os vetores não estão em nossa fatia . Assim, embora tenhamos encontrado uma hipersuperfície espacial, ela é ortogonal às linhas de mundo de apenas alguns de nossos observadores Langevin. Como a obstrução do teorema de Frobenius pode ser entendida em termos da falha dos campos vetoriais em formar uma álgebra de Lie , essa obstrução é diferencial, na verdade, teórica de Lie. Ou seja, é uma espécie de obstrução infinitesimal à existência de uma noção satisfatória de hiperslices espaciais para nossos observadores rotativos. ${\ displaystyle {\ vec {p}} _ {2}, \, {\ vec {p}} _ {3}}$${\ displaystyle {\ vec {p}} _ {2}}$ ${\ displaystyle {\ vec {p}} _ {2}, \, {\ vec {p}} _ {3}}$

Em segundo lugar, como mostra a Fig. 3, nossa tentativa de hiperslice levaria a uma noção descontínua de "tempo" devido aos "saltos" nas curvas integrais (mostradas como uma descontinuidade de grade de cor azul). Como alternativa, podemos tentar usar um tempo de vários valores. Nenhuma dessas alternativas parece muito atraente! Evidentemente, trata-se de uma obstrução global . É claro que é uma consequência de nossa incapacidade de sincronizar os relógios dos observadores Langevin montando um único anel - digamos a borda de um disco - muito menos um disco inteiro .

O efeito Sagnac

Imagine que prendemos um cabo de fibra óptica ao redor da circunferência de um anel que está girando com velocidade angular constante ω. Queremos calcular o tempo de viagem de ida e volta, medido por um observador em anel, para um pulso de laser enviado no sentido horário e anti-horário ao redor do cabo. Para simplificar, ignoraremos o fato de que a luz viaja através de um cabo de fibra óptica a um pouco menos que a velocidade da luz no vácuo e fingiremos que a linha de mundo de nosso pulso de laser é uma curva nula (mas certamente não uma geodésica nula !).

No elemento da linha Born, vamos colocar . Isto dá ${\ displaystyle \ mathrm {d} s = \ mathrm {d} z = \ mathrm {d} r = 0}$

${\ displaystyle (1- \ omega ^ {2} \, r_ {0} ^ {2}) \, \ mathrm {d} t ^ {2} = 2 \ omega \, r_ {0} ^ {2} \ , \ mathrm {d} t \, \ mathrm {d} \ phi + r_ {0} ^ {2} \, \ mathrm {d} \ phi ^ {2}}$

ou

${\ displaystyle \ mathrm {d} t _ {+} = {\ frac {r_ {0} \, \ mathrm {d} \ phi} {1- \ omega \, r_ {0}}}, \ quad \ mathrm { d} t _ {-} = - {\ frac {r_ {0} \, \ mathrm {d} \ phi} {1+ \ omega \, r_ {0}}}}$

Obtemos para o tempo de viagem de ida e volta

${\ displaystyle \ Delta t _ {+} = \ int _ {0} ^ {2 \ pi} {\ frac {r_ {0} \, \ mathrm {d} \ phi} {1- \ omega \, r_ {0 }}} = {\ frac {2 \ pi r_ {0}} {1- \ omega \, r_ {0}}}, \ quad \ Delta t _ {-} = \ int _ {0} ^ {- 2 \ pi} - {\ frac {r_ {0} \, \ mathrm {d} \ phi} {1+ \ omega \, r_ {0}}} = {\ frac {2 \ pi r_ {0}} {1+ \ omega \, r_ {0}}}}$

Colocando , encontramos (ω positivo significa rotação no sentido anti-horário, ω negativo significa rotação no sentido horário) para que os observadores do ringue possam determinar a velocidade angular do anel (medida por um observador estático) a partir da diferença entre o deslocamento no sentido horário e anti-horário vezes. Isso é conhecido como efeito Sagnac . É evidentemente um efeito global . ${\ displaystyle \ delta = {\ frac {\ Delta t _ {+} - \ Delta t _ {-}} {2 \, \ pi \, r_ {0}}}}$${\ displaystyle \ omega _ {+, -} = {\ frac {-1 \ pm {\ sqrt {1+ \ delta ^ {2}}}} {r_ {0} \, \ delta}}}$

Geodésica Nula

Fig. 4: Duas trilhas geodésicas nulas radiais (curva verde: limite externo, curva vermelha: limite interno) representadas no gráfico de Born. A trilha de um observador Langevin L orbitando no sentido anti-horário no raio R = R ₀ , ou seja, andando em um anel giratório no sentido anti-horário, também é mostrada (círculo azul marinho). Parâmetros: ω = +0,2, R ₀ = r ₀ = 1

Queremos comparar a aparência de geodésicas nulas na carta cilíndrica e na carta de Born.

No gráfico cilíndrico, as equações geodésicas leem

${\ displaystyle {\ ddot {T}} = 0, \; \; {\ ddot {Z}} = 0, \; \; {\ ddot {R}} - R \, {\ ponto {\ Phi}} ^ {2} = 0, \; \; {\ ddot {\ Phi}} + {\ frac {2} {R}} \, {\ dot {\ Phi}} \, {\ dot {R}} = 0.}$

Nós imediatamente obtemos as primeiras integrais

${\ displaystyle {\ dot {T}} = E, \; \; {\ dot {Z}} = P, \; \; {\ dot {\ Phi}} = {\ frac {L} {R ^ { 2}}}.}$

Conectando-os à expressão obtida a partir do elemento de linha por configuração , obtemos ${\ displaystyle \ mathrm {d} s ^ {2} = 0}$

${\ displaystyle {\ dot {R}} ^ {2} = E ^ {2} -P ^ {2} - {\ frac {L ^ {2}} {R ^ {2}}} \ geq 0}$

a partir do qual vemos que o raio mínimo de uma geodésica nula é dado por

${\ displaystyle E ^ {2} -P ^ {2} - {\ frac {L ^ {2}} {R _ {\ mathrm {min}} ^ {2}}} = 0 \ quad}$ ou seja, ${\ displaystyle \ quad R _ {\ mathrm {min}} = {\ frac {| L |} {\ sqrt {E ^ {2} -P ^ {2}}}}}$

portanto

${\ displaystyle {\ dot {R}} ^ {2} = L ^ {2} \ left ({\ frac {1} {R _ {\ mathrm {min}} ^ {2}}} - {\ frac {1 } {R ^ {2}}} \ right).}$

Fig. 5: Geodésicas nulas representadas na carta de Born entre observadores de Langevin montados no anel ( r = r ₀ = 1). As geodésicas nulas que se propagam com a rotação são dobradas para dentro (curva verde), as geodésicas nulas que se propagam contra a rotação são dobradas para fora (curva vermelha). O tempo de viagem da luz adequado de L ₁ a L ₂ Δ t ₁₂ é 1,311, de L ₂ a L ₁ Δ t ₂₁ é 1,510, os tempos de viagem da luz adequados não são simétricos, mas a distância do radar (Δ t ₁₂ + Δ t ₂₁ ) / 2 é. Para ω → 0, ambos os tempos adequados de viagem da luz tendem a √ 2 = 1,414. Geodésicas nulas entre observadores Langevin opostos (L ₁ e L ₃ ) dobram simetricamente em torno do centro de rotação. Parâmetros: ω = +0,1, R ₀ = r ₀ = 1, Δ ϕ (L ₁ , L ₂ ) = π / 2, Δ ϕ (L ₁ , L ₃ ) = π

Podemos agora resolver para obter as geodésicas nulas como curvas parametrizadas por um parâmetro afim, da seguinte maneira:

${\ displaystyle {\ begin {alinhados} R & = {\ sqrt {(E ^ {2} -P ^ {2}) \, s ^ ​​{2} + L ^ {2} / (E ^ {2} -P ^ {2})}} = \\ & = {\ sqrt {(E ^ {2} -P ^ {2}) \, s ^ ​​{2} + R _ {\ mathrm {min}} ^ {2}} }, \\ T & = T_ {0} + E \, s, \\ [1em] Z & = Z_ {0} + P \, s, \\\ Phi & = \ Phi _ {0} + \ operatorname {arctan } \ left ({\ frac {E ^ {2} -P ^ {2}} {L}} \, s \ right) = \\ & = \ Phi _ {0} + \ operatorname {arctan} \ left ( {\ frac {\ sqrt {E ^ {2} -P ^ {2}}} {R _ {\ mathrm {min}} \, \ operatorname {sgn} {(L)}}} \, s \ direita). \ end {alinhado}}}$

Mais útil para nossos propósitos é a observação de que a trajetória de uma geodésica nula (sua projeção em qualquer hiperslice espacial ) é, naturalmente, uma linha reta, dada por ${\ displaystyle T = T_ {0}}$

${\ displaystyle R = R _ {\ mathrm {min}} \, \ sec (\ Phi - \ Phi _ {0}).}$

Para obter o raio mínimo da linha através de dois pontos (do mesmo lado do ponto de aproximação mais próximo à origem), resolvemos

${\ displaystyle R_ {1} = R _ {\ mathrm {min}} \, \ sec (\ Phi _ {1} - \ Phi _ {0}), \; \; R_ {2} = R _ {\ mathrm { min}} \, \ sec (\ Phi _ {2} - \ Phi _ {0})}$

que dá

${\ displaystyle R _ {\ mathrm {min}} = {\ frac {R_ {1} \, R_ {2} \, | \ sin (\ Phi _ {2} - \ Phi _ {1}) |} {\ sqrt {R_ {1} ^ {2} -2 \, R_ {1} \, R_ {2} \, \ cos (\ Phi _ {2} - \ Phi _ {1}) + R_ {2} ^ { 2}}}}.}$

Agora considere o caso mais simples, a geodésica nula radial (R _min = L = 0, E = 1, P = 0). Uma geodésica nula radial de limite externo pode ser escrita na forma

${\ displaystyle T = s, \; Z = Z_ {0}, \; R = s,}$

${\ displaystyle \ Phi = \ mathrm {const.} = \ omega \, R_ {0}}$

com o raio R ₀ do anel montado no observador Langevin (ver Fig. 4). Transformando para o gráfico de Born, descobrimos que a trajetória pode ser escrita como

${\ displaystyle r = r_ {0} - {\ frac {\ phi} {\ omega}}.}$

As trilhas aparecem ligeiramente curvadas no gráfico de Born (veja a curva verde na Fig. 4). Na seção Transformando para o gráfico de Born , vemos que no gráfico de Born não podemos nos referir adequadamente a essas "trilhas" como "projeções", pois para o observador de Langevin um hiperslice ortogonal para t = t ₀ não existe (ver Fig. 3) .

Da mesma forma, para geodésicas nulas radiais de limite interno, obtemos

${\ displaystyle r = {\ frac {\ phi} {\ omega}}}$

representado como curva vermelha na Fig. 4.

Observe que para enviar um pulso de laser em direção ao observador estacionário S em R = 0, o observador Langevin L deve apontar ligeiramente para trás para corrigir seu próprio movimento. Virando as coisas, assim como um caçador de patos esperaria, para enviar um pulso de laser em direção ao observador Langevin montado em um anel giratório no sentido anti-horário, o observador central deve mirar, não na posição atual do observador, mas na posição em que ele chegará bem a tempo de interceptar o sinal. Essas famílias de geodésicas nulas radiais de limite interno e externo representam curvas muito diferentes no espaço-tempo e suas projeções não concordam para ω> 0.

Fig. 6: Um arco geodésico nulo, representado na carta de Born, que modela um sinal enviado de um observador circular para outro. As linhas de mundo desses observadores são mostradas como linhas verticais azuis; o centro de simetria como uma linha vertical verde. Observe que nosso geodésico nulo (arco âmbar) parece curvar ligeiramente para dentro (veja também a curva verde na Fig. 5).

Da mesma forma, geodésicas nulas entre observadores de Langevin em anel aparecem ligeiramente curvados para dentro na carta de Born, se as geodésicas se propagam com a direção da rotação (veja a curva verde na Fig. 5). Para ver isso, escreva a equação de uma geodésica nula no gráfico cilíndrico no formulário

${\ displaystyle T = R _ {\ mathrm {min}} \, \ tan (\ Phi),}$

${\ displaystyle R = R _ {\ mathrm {min}} \, \ sec (\ Phi).}$

Transformando em coordenadas de Born, obtemos as equações

${\ displaystyle t = r _ {\ mathrm {min}} \, \ tan (\ phi + \ omega \, t),}$

${\ displaystyle r = r _ {\ mathrm {min}} \, \ sec (\ phi + \ omega \, t).}$

Eliminando ϕ dá

${\ displaystyle r = {\ sqrt {r _ {\ mathrm {min}} ^ {2} + t ^ {2}}}}$

o que mostra que a geodésica de fato parece curvar-se para dentro (ver Fig. 6). Nós também achamos que

${\ displaystyle \ phi = - \ omega \, t + \ operatorname {arctan} (t / r _ {\ mathrm {min}}).}$

Para geodésicas nulas propagando contra a rotação (curva vermelha na Fig. 5), obtemos

${\ displaystyle r = {\ sqrt {r _ {\ mathrm {min}} ^ {2} + t ^ {2}}},}$

${\ displaystyle \ phi = - \ omega \, t- \ operatorname {arctan} (t / r _ {\ mathrm {min}})}$

e as curvas geodésicas ligeiramente para fora. Isso completa a descrição do aparecimento de geodésicas nulas no gráfico de Born, uma vez que toda geodésica nula é radial ou então tem algum ponto de aproximação mais próxima ao eixo de simetria cilíndrica.

Observe (ver Fig. 5) que um observador que está em anel tentando enviar um pulso de laser para outro observador em anel deve apontar um pouco para frente ou para trás de sua coordenada angular, conforme fornecido no gráfico de Born, a fim de compensar o movimento rotacional do alvo. Observe também que a imagem apresentada aqui é totalmente compatível com nossa expectativa (veja a aparência do céu noturno ) de que um observador em movimento verá a posição aparente de outros objetos em sua esfera celeste a serem deslocados na direção de seu movimento.

Distância de radar em grande

Fig. 7: Esta figura esquemática ilustra a noção de distância de radar entre um observador em anel e um observador central estático (com a mesma coordenada Z ).

Mesmo em um espaço-tempo plano, verifica-se que observadores em aceleração (mesmo observadores em aceleração linear; consulte as coordenadas de Rindler ) podem empregar várias noções de distância distintas, mas operacionalmente significativas. Talvez a mais simples delas seja a distância do radar .

Considere como um observador estático em R = 0 pode determinar sua distância para um observador em anel em R = R ₀ . No evento C, ele envia um pulso de radar em direção ao anel, que atinge a linha de mundo de um observador em A ′ e então retorna ao observador central no evento C ″. (Veja o diagrama do lado direito na Fig. 7.) Ele então divide o tempo decorrido (medido por um relógio ideal que ele carrega) por dois. Não é difícil ver que ele obtém para esta distância simplesmente R ₀ (no gráfico cilíndrico), ou r ₀ (no gráfico de Born).

Da mesma forma, um observador em anel pode determinar sua distância ao observador central enviando um pulso de radar, no evento A em direção ao observador central, que atinge sua linha mundial no evento C ′ e retorna ao observador em anel no evento A ″ . (Veja o diagrama à esquerda na Fig. 7.) Não é difícil ver que ele obtém para esta distância (no gráfico cilíndrico) ou (no gráfico de Born), um resultado um pouco menor que o obtido pelo observador central. Isso é uma consequência da dilatação do tempo: o tempo decorrido para um observador em anel é menor pelo fator do que o tempo para o observador central. Assim, embora a distância do radar tenha um significado operacional simples, ela nem mesmo é simétrica . ${\ displaystyle R_ {0} {\ sqrt {1- \ omega ^ {2} \, R_ {0} ^ {2}}}}$${\ displaystyle r_ {0} {\ sqrt {1- \ omega ^ {2} \, r_ {0} ^ {2}}}}$${\ displaystyle {\ sqrt {1- \ omega ^ {2} \, r_ {0} ^ {2}}}}$

Fig. 8: Esta figura esquemática ilustra a noção de distância de radar entre dois observadores Langevin montando um anel com raio R ₀ que está girando com velocidade angular ω . No diagrama à esquerda, o anel está girando no sentido anti-horário; no diagrama à direita, ele está girando no sentido horário.

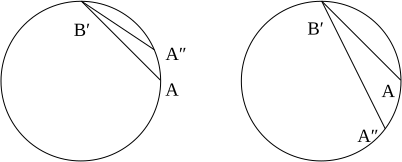
Para esclarecer este ponto crucial, compare as distâncias de radar obtidas por dois observadores em anel com coordenada radial R = R ₀ . No diagrama do lado esquerdo da Fig. 8, podemos escrever as coordenadas do evento A como

${\ displaystyle T = 0, \; Z = 0, \; X = R_ {0}, Y = 0}$

e podemos escrever as coordenadas do evento B ′ como

${\ displaystyle T = 2 \, R_ {0} \, \ sin \ left ({\ frac {\ Phi} {2}} \ right), \; Z = 0,}$

${\ displaystyle X = R_ {0} \ cos (\ Phi), \; Y = R_ {0} \ sin (\ Phi)}$

Escrevendo o tempo próprio decorrido desconhecido como , agora escrevemos as coordenadas do evento A ″ como ${\ displaystyle \ Delta s}$

${\ displaystyle T = {\ frac {\ Delta s} {\ sqrt {1- \ omega ^ {2} \, R_ {0} ^ {2}}}}, \; Z = 0}$

${\ displaystyle X = R_ {0} \ cos \ left ({\ frac {\ omega \, \ Delta s} {\ sqrt {1- \ omega ^ {2} \, R_ {0} ^ {2}}} } \ right), \; Y = R_ {0} \ sin \ left ({\ frac {\ omega \, \ Delta s} {\ sqrt {1- \ omega ^ {2} \, R_ {0} ^ { 2}}}} \ right)}$

Exigindo que os segmentos de linha que conectam esses eventos sejam nulos, obtemos uma equação que, em princípio, podemos resolver para Δ s . Acontece que este procedimento fornece uma equação não linear bastante complicada, portanto, simplesmente apresentamos alguns resultados numéricos representativos. Com R ₀ = 1, Φ = π / 2 e ω = 1/10, descobrimos que a distância do radar de A a B é de cerca de 1,311, enquanto a distância de B a A é de cerca de 1,510. Como ω tende a zero, ambos os resultados tendem a √ 2 = 1,414 (veja também a Fig. 5).

Apesar dessas discrepâncias possivelmente desencorajadoras, não é de forma alguma impossível conceber um gráfico de coordenadas que seja adaptado para descrever a experiência física de um único observador Langevin, ou mesmo de um único observador acelerando arbitrariamente no espaço-tempo de Minkowski. Pauri e Vallisneri adaptaram o procedimento de sincronização do relógio de Märzke-Wheeler para criar coordenadas adaptadas que eles chamam de coordenadas de Märzke-Wheeler (veja o artigo citado abaixo). No caso de movimento circular constante, este gráfico está de fato intimamente relacionado à noção de distância de radar "no grande" de um determinado observador de Langevin.

Distância de radar no pequeno

Como foi mencionado acima , por várias razões, a família de observadores de Langevin não admite nenhuma família de hiperslices ortogonais. Portanto, esses observadores simplesmente não podem ser associados a qualquer divisão do espaço-tempo em uma família de "fatias de tempo constantes" sucessivas.

No entanto, como a congruência de Langevin é estacionária , podemos imaginar a substituição de cada linha de mundo nesta congruência por um ponto . Ou seja, podemos considerar o espaço quociente do espaço -tempo de Minkowski (ou melhor, a região 0 < R <1 / ω ) pela congruência de Langevin, que é uma variedade topológica tridimensional . Melhor ainda, podemos colocar uma métrica Riemanniana nesta variedade quociente, transformando-a em uma variedade Riemanniana tridimensional , de forma que a métrica tenha um significado operacional simples.

Para ver isso, considere o elemento da linha Born

${\ displaystyle \ mathrm {d} s ^ {2} = - (1- \ omega ^ {2} \, r ^ {2}) \, \ mathrm {d} t ^ {2} +2 \, \ omega \, r ^ {2} \, \ mathrm {d} t \, \ mathrm {d} \ phi + \ mathrm {d} z ^ {2} + \ mathrm {d} r ^ {2} + r ^ { 2} \, \ mathrm {d} \ phi ^ {2},}$

${\ displaystyle - \ infty <t, z <\ infty, \; \; 0 <r <{\ frac {1} {\ omega}}, \; \; - \ pi <\ phi <\ pi.}$

Definindo d s ² = 0 e resolvendo para d t , obtemos

${\ displaystyle \ mathrm {d} t _ {+} = {\ frac {\ omega \, r ^ {2} \, \ mathrm {d} \ phi + {\ sqrt {(1- \ omega ^ {2} \ , r ^ {2}) \; (\ mathrm {d} z ^ {2} + \ mathrm {d} r ^ {2}) + r ^ {2} \, \ mathrm {d} \ phi ^ {2 }}}} {1- \ omega ^ {2} \, r ^ {2}}},}$

${\ displaystyle \ mathrm {d} t _ {-} = {\ frac {\ omega \, r ^ {2} \, \ mathrm {d} \ phi - {\ sqrt {(1- \ omega ^ {2} \ , r ^ {2}) \; (\ mathrm {d} z ^ {2} + \ mathrm {d} r ^ {2}) + r ^ {2} \, \ mathrm {d} \ phi ^ {2 }}}} {1- \ omega ^ {2} \, r ^ {2}}}.}$

O tempo adequado decorrido para um blip de radar de ida e volta emitido por um observador Langevin é então

${\ displaystyle {\ sqrt {1- \ omega ^ {2} \, r ^ {2}}} \; {\ frac {\ mathrm {d} t _ {+} - \ mathrm {d} t _ {-}} {2}} = {\ sqrt {\ mathrm {d} z ^ {2} + \ mathrm {d} r ^ {2} + {\ frac {r ^ {2} \, \ mathrm {d} \ phi ^ {2}} {1- \ omega ^ {2} \, r ^ {2}}}}}.}$

Portanto, em nossa variedade quociente, o elemento de linha Riemanniana

${\ displaystyle \ mathrm {d} \ sigma ^ {2} = \ mathrm {d} z ^ {2} + \ mathrm {d} r ^ {2} + {\ frac {r ^ {2} \, \ mathrm {d} \ phi ^ {2}} {1- \ omega ^ {2} \, r ^ {2}}},}$

${\ displaystyle - \ infty <t <\ infty, \; \; 0 <r <{\ frac {1} {\ omega}}, \; \; - \ pi <\ phi <\ pi}$

corresponde à distância entre observadores Langevin infinitesimalmente próximos . Vamos chamá-la de métrica Langevin-Landau-Lifschitz , e podemos chamar essa noção de distância de radar de distância "no pequeno" .

Esta métrica foi dada pela primeira vez por Langevin , mas a interpretação em termos de distância de radar "no pequeno" é devida a Lev Landau e Evgeny Lifshitz , que generalizou a construção para trabalhar para o quociente de qualquer variedade Lorentziana por uma congruência temporal estacionária .

Se adotarmos o coframe

${\ displaystyle \ theta ^ {\ hat {1}} = \ mathrm {d} z, \; \; \ theta ^ {\ hat {2}} = \ mathrm {d} r, \; \; \ theta ^ {\ hat {3}} = {\ frac {r \, \ mathrm {d} \ phi} {\ sqrt {1- \ omega ^ {2} \, r ^ {2}}}}}$

podemos calcular facilmente o tensor de curvatura Riemanniano de nossa variedade quociente tridimensional. Tem apenas dois componentes não triviais independentes,

${\ displaystyle {R ^ {\ hat {2}}} _ {{\ hat {3}} {\ hat {2}} {\ hat {3}}} = {\ frac {-3 \, \ omega ^ {2}} {(1- \ omega ^ {2} r ^ {2}) ^ {2}}} = - 3 \, \ omega ^ {2} + O (\ omega ^ {4} \, r ^ {2}),}$

${\ displaystyle {R ^ {\ hat {3}}} _ {{\ hat {2}} {\ hat {3}} {\ hat {2}}} = {\ frac {-3 \, \ omega ^ {2} \, r ^ {2}} {(1- \ omega ^ {2} r ^ {2}) ^ {3}}} = - 3 \, \ omega ^ {2} \, r ^ {2 } + O (\ omega ^ {4} \, r ^ {4}).}$

Assim, em certo sentido, a geometria de um disco giratório é curva , como Theodor Kaluza alegou (sem prova) já em 1910. Na verdade, para a segunda ordem em ω, ele tem a geometria do plano hiperbólico, assim como Kaluza alegou.

Aviso: como vimos, há muitas noções possíveis de distância que podem ser empregadas por observadores Langevin que montam em um disco rotativo rígido; portanto, as declarações referentes à "geometria de um disco rotativo" sempre requerem uma qualificação cuidadosa.

Para esclarecer este ponto importante, vamos usar a métrica Landau-Lifschitz para calcular a distância entre um observador Langevin andando em um anel com raio R ₀ e um observador estático central. Para fazer isso, precisamos apenas integrar nosso elemento de linha sobre a trilha geodésica nula apropriada. Em nosso trabalho anterior, vemos que devemos conectar

${\ displaystyle \ mathrm {d} r = {\ frac {\ mathrm {d} \ phi} {\ omega}}, \, \ mathrm {d} z = 0}$

em nosso elemento de linha e integrar

${\ displaystyle \ int _ {0} ^ {\ Delta} \ mathrm {d} \ sigma = \ int \ limits _ {0} ^ {r_ {0}} {\ left (1 + {\ frac {\ omega ^ {2} r ^ {2}} {1- \ omega ^ {2} r ^ {2}}} \ right) ^ {\ frac {1} {2}}} \, \ mathrm {d} r.}$

Isto dá

${\ displaystyle \ Delta = \ int _ {0} ^ {r_ {0}} {\ frac {\ mathrm {d} r} {\ sqrt {1- \ omega ^ {2} \, r ^ {2}} }} = {\ frac {\ arcsin (\ omega r_ {0})} {\ omega}} = r_ {0} + {\ frac {\ omega ^ {2} \, r_ {0} ^ {3}} {6}} + O (r_ {0} ^ {5}).}$

Como agora estamos lidando com uma métrica Riemanniana, essa noção de distância é obviamente simétrica com a troca de dois observadores, ao contrário da distância de radar "no grande". Os valores dados por esta noção estão em contradição com as distâncias de radar "no grande" calculadas na seção anterior. Além disso, porque até a segunda ordem a métrica de Landau-Lifschitz concorda com a convenção de sincronização de Einstein, vemos que o tensor de curvatura que acabamos de calcular tem significado operacional: enquanto a distância de radar "no grande" entre pares de observadores Langevin certamente não é um Noção Riemanniana de distância , a distância entre pares de observadores Langevin próximos corresponde a uma distância Riemanniana, dada pela métrica Langevin-Landau-Lifschitz. (Na frase feliz de Howard Percy Robertson , isso é cinemática im Kleinen .)

Uma maneira de ver que todas as noções razoáveis ​​de distância espacial para nossos observadores Langevin concordam com os observadores próximos é mostrar, seguindo Nathan Rosen , que para qualquer observador Langevin, um observador inercial co-movendo instantaneamente também obterá as distâncias dadas pelo Langevin -Landau-Lifschitz métrica, para distâncias muito pequenas.

Veja também

• Paradoxo de Ehrenfest , para um tópico às vezes controverso frequentemente estudado usando o gráfico de Born.
• Giroscópio de fibra óptica
• Coordenadas de Rindler , para outra carta de coordenadas útil adaptada a outra família importante de observadores acelerados no espaço-tempo de Minkowski ; este artigo também enfatiza a existência de noções distintas de distância que podem ser empregadas por tais observadores.
• Efeito Sagnac

Referências

Alguns papéis de interesse histórico:

• Nascido, M. (1909). "Die Theorie des starren Elektrons in der Kinematik des Relativitäts-Prinzipes" . Ann. Phys . 30 (11): 1-56. Bibcode : 1909AnP ... 335 .... 1B . doi : 10.1002 / andp.19093351102 .
  • Tradução do Wikisource: A Teoria do Elétron Rígido na Cinemática do Princípio da Relatividade
• Ehrenfest, P. (1909). "Gleichförmige Rotation starrer Körper und Relativitätstheorie". Phys. Z . 10 : 918. bibcode : 1909PhyZ ... 10..918E .
  • Tradução do Wikisource: Rotação Uniforme de Corpos Rígidos e a Teoria da Relatividade
• Langevin, P. (1935). "Remarques au sujet de la Note de Prunier". CR Acad. Sci. Paris . 200 : 48.

Algumas referências clássicas:

• Grøn, Ø. (1975). "Descrição relativística de um disco giratório". Sou. J. Phys . 43 (10): 869–876. Bibcode : 1975AmJPh..43..869G . doi : 10.1119 / 1.9969 .
• Landau, LD & Lifschitz, EM (1980). The Classical Theory of Fields (4ª ed.) . Londres: Butterworth-Heinemann. ISBN 0-7506-2768-9. Veja a Seção 84 para a métrica Landau-Lifschitz sobre o quociente de uma variedade Lorentziana por uma congruência estacionária ; veja o problema no final da Seção 89 para a aplicação aos observadores Langevin.

Fontes recentes selecionadas:

• Rizzi, G. & Ruggiero, ML (2004). Relatividade em quadros rotativos . Dordrecht: Kluwer. ISBN 1-4020-1805-3. Este livro contém uma valiosa pesquisa histórica de Øyvind Grøn e alguns outros artigos sobre o paradoxo de Ehrenfest e controvérsias relacionadas e um artigo de Lluis Bel discutindo a congruência Langevin. Centenas de referências adicionais podem ser encontradas neste livro.
• Pauri, Massimo e Vallisneri, Michele (2000). "Coordenadas de Märzke-Wheeler para observadores acelerados na relatividade especial". Encontrado. Phys. Lett . 13 (5): 401–425. Bibcode : 2000gr.qc ..... 6095P . doi : 10.1023 / A: 1007861914639 . S2CID  15097773 .Estuda um gráfico de coordenadas construído usando a distância de radar "em grande" de um único observador Langevin. Veja também a versão eprint .

links externos

• The Rigid Rotating Disk in Relativity , de Michael Weiss (1995), do sci.physics FAQ .