Relatividade especial -Special relativity

| Relatividade especial |
|---|
 |
Na física , a teoria da relatividade especial , ou relatividade especial , é uma teoria científica sobre a relação entre espaço e tempo . No tratamento original de Albert Einstein , a teoria é baseada em dois postulados :
- As leis da física são invariantes (isto é, idênticas) em todos os referenciais inerciais (isto é, referenciais sem aceleração ).
- A velocidade da luz no vácuo é a mesma para todos os observadores, independentemente do movimento da fonte de luz ou do observador.
Origens e significado
A relatividade especial foi originalmente proposta por Albert Einstein em um artigo publicado em 26 de setembro de 1905 intitulado " Sobre a eletrodinâmica dos corpos em movimento ". A incompatibilidade da mecânica newtoniana com as equações de eletromagnetismo de Maxwell e, experimentalmente, o resultado nulo de Michelson-Morley (e experimentos semelhantes subsequentes) demonstraram que o éter luminífero historicamente hipotético não existia. Isso levou ao desenvolvimento da relatividade especial de Einstein, que corrige a mecânica para lidar com situações que envolvem todos os movimentos e especialmente aqueles a uma velocidade próxima à da luz (conhecida como velocidades relativísticas ). Hoje, a relatividade especial provou ser o modelo mais preciso de movimento em qualquer velocidade quando os efeitos gravitacionais e quânticos são insignificantes. Mesmo assim, o modelo newtoniano ainda é válido como uma aproximação simples e precisa em baixas velocidades (relativas à velocidade da luz), por exemplo, movimentos cotidianos na Terra.
A relatividade especial tem uma ampla gama de consequências que foram verificadas experimentalmente. Eles incluem a relatividade da simultaneidade , contração do comprimento , dilatação do tempo , a fórmula de adição de velocidade relativística , o efeito Doppler relativístico , massa relativística , um limite de velocidade universal , equivalência massa-energia , a velocidade de causalidade e a precessão de Thomas . Ela substituiu, por exemplo, a noção convencional de um tempo universal absoluto pela noção de um tempo que depende do referencial e da posição espacial . Em vez de um intervalo de tempo invariável entre dois eventos, existe um intervalo de espaço -tempo invariável . Combinados com outras leis da física, os dois postulados da relatividade especial prevêem a equivalência de massa e energia , conforme expresso na fórmula de equivalência massa-energia , onde é a velocidade da luz no vácuo. Também explica como os fenômenos da eletricidade e do magnetismo estão relacionados.
Uma característica definidora da relatividade especial é a substituição das transformações galileanas da mecânica newtoniana pelas transformações de Lorentz . Tempo e espaço não podem ser definidos separadamente um do outro (como se pensava anteriormente). Em vez disso, espaço e tempo estão entrelaçados em um único continuum conhecido como "espaço-tempo" . Eventos que ocorrem ao mesmo tempo para um observador podem ocorrer em momentos diferentes para outro.
Até Einstein desenvolver a relatividade geral , introduzindo um espaço-tempo curvo para incorporar a gravidade, a expressão "relatividade especial" não era usada. Uma tradução às vezes usada é "relatividade restrita"; "especial" realmente significa "caso especial". Alguns dos trabalhos de Albert Einstein em relatividade especial são construídos sobre os trabalhos anteriores de Hendrik Lorentz e Henri Poincaré . A teoria tornou-se essencialmente completa em 1907.
A teoria é "especial" na medida em que só se aplica no caso especial onde o espaço-tempo é "plano", ou seja, a curvatura do espaço -tempo , consequência do tensor energia-momento e representando a gravidade , é desprezível. A fim de acomodar corretamente a gravidade, Einstein formulou a relatividade geral em 1915. A relatividade especial, ao contrário de algumas descrições históricas, acomoda tanto acelerações quanto referenciais acelerados .
Assim como a relatividade galileana é agora aceita como uma aproximação da relatividade especial válida para baixas velocidades, a relatividade especial é considerada uma aproximação da relatividade geral válida para campos gravitacionais fracos , isto é, em uma escala suficientemente pequena (por exemplo, quando forças de maré são desprezíveis) e em condições de queda livre . A relatividade geral, no entanto, incorpora a geometria não-euclidiana para representar os efeitos gravitacionais como a curvatura geométrica do espaço-tempo. A relatividade especial é restrita ao espaço-tempo plano conhecido como espaço de Minkowski . Desde que o universo possa ser modelado como uma variedade pseudo-Riemanniana , um referencial invariante de Lorentz que obedece à relatividade especial pode ser definido para uma vizinhança suficientemente pequena de cada ponto neste espaço- tempo curvo .
Galileu Galilei já havia postulado que não existe um estado de repouso absoluto e bem definido (nenhum referencial privilegiado ), princípio agora chamado de princípio da relatividade de Galileu . Einstein estendeu esse princípio de modo que explicasse a velocidade constante da luz, um fenômeno que havia sido observado no experimento de Michelson-Morley. Ele também postulou que vale para todas as leis da física , incluindo as leis da mecânica e da eletrodinâmica .
Abordagem tradicional de "dois postulados" para a relatividade especial
"Reflexões desse tipo deixaram claro para mim já logo após 1900, ou seja, logo após o trabalho pioneiro de Planck, que nem a mecânica nem a eletrodinâmica poderiam (exceto em casos limites) reivindicar validade exata. as verdadeiras leis por meio de esforços construtivos baseados em fatos conhecidos. Quanto mais e mais desesperadamente eu tentava, mais eu me convencia de que somente a descoberta de um princípio formal universal poderia nos levar a resultados seguros... Como, então, , poderia tal princípio universal ser encontrado?"
Albert Einstein: notas autobiográficas
Einstein discerniu duas proposições fundamentais que pareciam ser as mais seguras, independentemente da validade exata das (então) conhecidas leis da mecânica ou da eletrodinâmica. Essas proposições eram a constância da velocidade da luz no vácuo e a independência das leis físicas (especialmente a constância da velocidade da luz) da escolha do sistema inercial. Em sua apresentação inicial da relatividade especial em 1905, ele expressou esses postulados como:
- O princípio da relatividade – as leis pelas quais os estados dos sistemas físicos sofrem mudanças não são afetadas, quer essas mudanças de estado sejam referidas a um ou outro de dois sistemas em movimento de translação uniforme um em relação ao outro.
- O princípio da velocidade da luz invariante - "... a luz é sempre propagada no espaço vazio com uma velocidade definida [velocidade] c que é independente do estado de movimento do corpo emissor" (do prefácio). Ou seja, a luz no vácuo se propaga com velocidade c (uma constante fixa, independente da direção) em pelo menos um sistema de coordenadas inerciais (o "sistema estacionário"), independentemente do estado de movimento da fonte de luz.
A constância da velocidade da luz foi motivada pela teoria do eletromagnetismo de Maxwell e pela falta de evidência do éter luminífero . Há evidências conflitantes sobre até que ponto Einstein foi influenciado pelo resultado nulo do experimento de Michelson-Morley . De qualquer forma, o resultado nulo do experimento de Michelson-Morley ajudou a noção da constância da velocidade da luz a ganhar ampla e rápida aceitação.
A derivação da relatividade especial depende não apenas desses dois postulados explícitos, mas também de várias suposições tácitas ( feitas em quase todas as teorias da física ), incluindo a isotropia e homogeneidade do espaço e a independência das hastes de medição e relógios de sua história passada.
Seguindo a apresentação original da relatividade especial de Einstein em 1905, muitos conjuntos diferentes de postulados foram propostos em várias derivações alternativas. No entanto, o conjunto de postulados mais comum continua sendo aquele empregado por Einstein em seu artigo original. Uma declaração mais matemática do princípio da relatividade feita mais tarde por Einstein, que introduz o conceito de simplicidade não mencionado acima, é:
Princípio especial da relatividade : Se um sistema de coordenadas K é escolhido de modo que, em relação a ele, as leis físicas sejam válidas em sua forma mais simples, as mesmas leis são válidas em relação a qualquer outro sistema de coordenadas K′ movendo-se em translação uniforme relativamente para K.
Henri Poincaré forneceu a estrutura matemática para a teoria da relatividade provando que as transformações de Lorentz são um subconjunto de seu grupo Poincaré de transformações de simetria. Mais tarde, Einstein derivou essas transformações de seus axiomas.
Muitos dos artigos de Einstein apresentam derivações da transformação de Lorentz com base nesses dois princípios.
Princípio da relatividade
Quadros de referência e movimento relativo

Os referenciais desempenham um papel crucial na teoria da relatividade. O termo referencial usado aqui é uma perspectiva observacional no espaço que não está sofrendo nenhuma mudança em movimento (aceleração), a partir do qual uma posição pode ser medida ao longo de 3 eixos espaciais (portanto, em repouso ou velocidade constante). Além disso, um quadro de referência tem a capacidade de determinar as medições do tempo dos eventos usando um 'relógio' (qualquer dispositivo de referência com periodicidade uniforme).
Um evento é uma ocorrência que pode ser atribuída a um único momento e localização únicos no espaço em relação a um quadro de referência: é um "ponto" no espaço -tempo . Como a velocidade da luz é constante na relatividade, independentemente do referencial, pulsos de luz podem ser usados para medir distâncias sem ambiguidade e se referir aos tempos em que os eventos ocorreram no relógio, mesmo que a luz demore para chegar ao relógio após o evento. aconteceu.
Por exemplo, a explosão de um foguete pode ser considerada um "evento". Podemos especificar completamente um evento por suas quatro coordenadas de espaço-tempo: O tempo de ocorrência e sua localização espacial tridimensional definem um ponto de referência. Vamos chamar este referencial de S .
Na teoria da relatividade, muitas vezes queremos calcular as coordenadas de um evento a partir de diferentes referenciais. As equações que relacionam medições feitas em diferentes quadros são chamadas de equações de transformação .
Configuração padrão
Para obter uma visão de como as coordenadas do espaço-tempo medidas pelos observadores em diferentes referenciais se comparam, é útil trabalhar com uma configuração simplificada com quadros em uma configuração padrão. Com cuidado, isso permite simplificar a matemática sem perda de generalidade nas conclusões a que se chega. Na Fig. 2-1, dois quadros de referência Galileanos (isto é, quadros convencionais de 3 espaços) são exibidos em movimento relativo. O quadro S pertence a um primeiro observador O, e o quadro S′ (pronuncia-se "S prime" ou "S dash") pertence a um segundo observador O′.
- Os eixos x , y , z do quadro S são orientados paralelamente aos respectivos eixos iniciados do quadro S'.
- O referencial S' se move, por simplicidade, em uma única direção: a direção x do referencial S com uma velocidade constante v medida no referencial S.
- As origens dos quadros S e S′ são coincidentes quando o tempo t = 0 para o quadro S e t ′ = 0 para o quadro S′.
Como não existe um referencial absoluto na teoria da relatividade, um conceito de 'mover' não existe estritamente, pois tudo pode estar se movendo em relação a algum outro referencial. Em vez disso, quaisquer dois quadros que se movem na mesma velocidade e na mesma direção são chamados de comoventes . Portanto, S e S ' não são comoventes .
Falta de um quadro de referência absoluto
O princípio da relatividade , que afirma que as leis físicas têm a mesma forma em cada referencial inercial , remonta a Galileu e foi incorporado à física newtoniana. No entanto, no final do século XIX, a existência de ondas eletromagnéticas levou alguns físicos a sugerirem que o universo estava repleto de uma substância que chamaram de " éter ", que, postularam, atuaria como o meio pelo qual essas ondas, ou vibrações, propagado (em muitos aspectos semelhante à forma como o som se propaga através do ar). O éter foi pensado para ser um referencial absoluto contra o qual todas as velocidades poderiam ser medidas, e poderia ser considerado fixo e imóvel em relação à Terra ou algum outro ponto de referência fixo. O éter deveria ser suficientemente elástico para suportar ondas eletromagnéticas, enquanto essas ondas podiam interagir com a matéria, mas não oferecendo resistência aos corpos que passavam por ela (sua única propriedade era permitir que as ondas eletromagnéticas se propagassem). Os resultados de vários experimentos, incluindo o experimento de Michelson-Morley em 1887 (posteriormente verificado com experimentos mais precisos e inovadores), levaram à teoria da relatividade especial, mostrando que o éter não existia. A solução de Einstein foi descartar a noção de éter e o estado absoluto de repouso. Na relatividade, qualquer referencial movendo-se com movimento uniforme observará as mesmas leis da física. Em particular, a velocidade da luz no vácuo é sempre medida como c , mesmo quando medida por vários sistemas que estão se movendo em velocidades diferentes (mas constantes).
Relatividade sem o segundo postulado
A partir do princípio da relatividade sozinho, sem assumir a constância da velocidade da luz (ou seja, usando a isotropia do espaço e a simetria implícita no princípio da relatividade especial) , pode-se mostrar que as transformações do espaço-tempo entre referenciais inerciais são euclidianas, galileanas , ou Lorentziano. No caso lorentziano, pode-se então obter a conservação do intervalo relativístico e uma certa velocidade limite finita. Experimentos sugerem que essa velocidade é a velocidade da luz no vácuo.
Invariância de Lorentz como o núcleo essencial da relatividade especial
Abordagens alternativas para a relatividade especial
Einstein baseou consistentemente a derivação da invariância de Lorentz (o núcleo essencial da relatividade especial) apenas nos dois princípios básicos da relatividade e da invariância da velocidade da luz. Ele escreveu:
O insight fundamental para a teoria da relatividade especial é este: As suposições da relatividade e da invariância da velocidade da luz são compatíveis se relações de um novo tipo ("transformação de Lorentz") forem postuladas para a conversão de coordenadas e tempos de eventos... O princípio universal da teoria da relatividade especial está contida no postulado: As leis da física são invariantes em relação às transformações de Lorentz (para a transição de um sistema inercial para qualquer outro sistema inercial arbitrariamente escolhido). Este é um princípio restritivo para as leis naturais...
Assim, muitos tratamentos modernos da relatividade especial a baseiam no postulado único da covariância universal de Lorentz, ou, equivalentemente, no postulado único do espaço-tempo de Minkowski .
Em vez de considerar a covariância universal de Lorentz como um princípio derivado, este artigo a considera o postulado fundamental da relatividade especial. A abordagem tradicional de dois postulados para a relatividade especial é apresentada em inúmeros livros universitários e apresentações populares. Os livros didáticos que começam com o postulado único do espaço-tempo de Minkowski incluem os de Taylor e Wheeler e os de Callahan. Esta é também a abordagem seguida pelos artigos da Wikipédia Spacetime e Minkowski diagram .
Transformação de Lorentz e sua inversa
Defina um evento para ter coordenadas de espaço-tempo ( t , x , y , z ) no sistema S e ( t ′, x ′, y ′, z ′) em um referencial movendo-se a uma velocidade v em relação a esse referencial, S ′ . Em seguida, a transformação de Lorentz especifica que essas coordenadas estão relacionadas da seguinte maneira:
Resolver as quatro equações de transformação acima para as coordenadas não prime produz a transformação inversa de Lorentz:
Forçar essa transformação de Lorentz inversa para coincidir com a transformação de Lorentz do sistema com primer para o sistema sem primer, mostra o referencial sem primer movendo-se com a velocidade v′ = − v , medida no referencial com primer.
Não há nada de especial sobre o eixo x . A transformação pode ser aplicada ao eixo y ou z , ou mesmo em qualquer direção paralela ao movimento (que são deformadas pelo fator γ ) e perpendicular; veja o artigo Transformação de Lorentz para detalhes.
Uma quantidade invariante sob transformações de Lorentz é conhecida como escalar de Lorentz .
Escrevendo a transformação de Lorentz e sua inversa em termos de diferenças de coordenadas, onde um evento tem coordenadas ( x 1 , t 1 ) e ( x ′ 1 , t ′ 1 ) , outro evento tem coordenadas ( x 2 , t 2 ) e ( x ′ 2 , t ′ 2 ) , e as diferenças são definidas como
- Eq. 1:
- Eq. 2:
Nós temos
- Eq. 3:
- Eq. 4:
Se tomarmos diferenciais em vez de diferenças, obtemos
- Eq. 5:
- Eq. 6:
Representação gráfica da transformação de Lorentz
Diagramas de espaço-tempo (diagramas de Minkowski ) são uma ajuda extremamente útil para visualizar como as coordenadas se transformam entre diferentes referenciais. Embora não seja tão fácil realizar cálculos exatos usando-os quanto invocando diretamente as transformações de Lorentz, seu principal poder é a capacidade de fornecer uma compreensão intuitiva dos resultados de um cenário relativístico.
Para desenhar um diagrama de espaço-tempo, comece considerando dois referenciais galileanos, S e S', na configuração padrão, como mostrado na Fig. 2-1.
Fig. 3-1a. Desenhe os eixos e do quadro S. O eixo é horizontal e o eixo (na verdade ) é vertical, o que é o oposto da convenção usual em cinemática. O eixo é dimensionado por um fator de de modo que ambos os eixos tenham unidades comuns de comprimento. No diagrama mostrado, as linhas de grade são espaçadas uma unidade de distância. As linhas diagonais de 45° representam as linhas do mundo de dois fótons passando pela origem no tempo. A inclinação dessas linhas do mundo é 1 porque os fótons avançam uma unidade no espaço por unidade de tempo. Dois eventos, e foram plotados neste gráfico para que suas coordenadas possam ser comparadas nos quadros S e S'.
Fig. 3-1b. Desenhe os eixos e do quadro S'. O eixo representa a linha de mundo da origem do sistema de coordenadas S' conforme medido no quadro S. Nesta figura, os eixos e são inclinados a partir dos eixos não iniciados por um ângulo em que os eixos iniciados e não iniciados compartilham uma origem comum porque os quadros S e S' foram configurados na configuração padrão, de modo que quando
Fig. 3-1c. As unidades nos eixos com primer têm uma escala diferente das unidades nos eixos sem primer. A partir das transformações de Lorentz, observamos que as coordenadas de no sistema de coordenadas com primer se transformam em no sistema de coordenadas sem primer. Da mesma forma, as coordenadas de no sistema de coordenadas com primer se transformam no sistema sem primer. Desenhe linhas de grade paralelas ao eixo através dos pontos medidos no quadro sem primer, onde é um número inteiro. Da mesma forma, desenhe linhas de grade paralelas ao eixo conforme medido no quadro sem primer. Usando o teorema de Pitágoras, observamos que o espaçamento entre unidades é igual a vezes o espaçamento entre unidades, medido no referencial S. Essa razão é sempre maior que 1 e, finalmente, se aproxima do infinito como
Fig. 3-1d. Como a velocidade da luz é invariante, as linhas de mundo de dois fótons que passam pela origem no momento ainda são traçadas como linhas diagonais de 45°. As coordenadas prime de e estão relacionadas com as coordenadas não prime através das transformações de Lorentz e podem ser medidas aproximadamente a partir do gráfico (assumindo que foi plotado com precisão suficiente), mas o verdadeiro mérito de um diagrama de Minkowski é nos conceder uma visão geométrica de o cenário. Por exemplo, nesta figura, observamos que os dois eventos separados no tempo que tinham diferentes coordenadas x no quadro não iniciado estão agora na mesma posição no espaço.
Enquanto o quadro sem primer é desenhado com eixos de espaço e tempo que se encontram em ângulos retos, o quadro com primer é desenhado com eixos que se encontram em ângulos agudos ou obtusos. Essa assimetria se deve a distorções inevitáveis em como as coordenadas do espaço-tempo são mapeadas em um plano cartesiano , mas os quadros são na verdade equivalentes.
Consequências derivadas da transformação de Lorentz
As consequências da relatividade especial podem ser derivadas das equações de transformação de Lorentz . Essas transformações e, portanto, a relatividade especial, levam a previsões físicas diferentes das da mecânica newtoniana em todas as velocidades relativas, e mais pronunciadas quando as velocidades relativas se tornam comparáveis à velocidade da luz. A velocidade da luz é muito maior do que qualquer coisa que a maioria dos humanos encontra que alguns dos efeitos previstos pela relatividade são inicialmente contraintuitivos .
Intervalo invariável
Na relatividade galileana, o comprimento ( ) e a separação temporal entre dois eventos ( ) são invariantes independentes, cujos valores não mudam quando observados a partir de diferentes referenciais.
Na relatividade especial, no entanto, o entrelaçamento de coordenadas espaciais e temporais gera o conceito de um intervalo invariante , denotado como :
O entrelaçamento de espaço e tempo revoga os conceitos implicitamente assumidos de simultaneidade absoluta e sincronização em quadros não móveis.
A forma de ser a diferença do quadrado do lapso de tempo e do quadrado da distância espacial, demonstra uma discrepância fundamental entre as distâncias euclidiana e espaço-temporal. A invariância desse intervalo é uma propriedade da transformada geral de Lorentz (também chamada de transformação de Poincaré ), tornando-se uma isometria do espaço-tempo. A transformada de Lorentz geral estende a transformada de Lorentz padrão (que lida com translações sem rotação, ou seja, Lorentz impulsiona , na direção x) com todas as outras translações , reflexões e rotações entre qualquer quadro inercial cartesiano.
Na análise de cenários simplificados, como diagramas de espaço-tempo, uma forma de dimensionalidade reduzida do intervalo invariante é frequentemente empregada:
Demonstrar que o intervalo é invariante é simples para o caso de dimensionalidade reduzida e com frames na configuração padrão:
O valor de é, portanto, independente do quadro em que é medido.
Ao considerar o significado físico de , há três casos a serem observados:
- Δs 2 > 0: Neste caso, os dois eventos são separados por mais tempo do que espaço e, portanto, são considerados separados no tempo . Isso implica que e dada a transformação de Lorentz é evidente que existe um menor que para o qual (em particular, ). Em outras palavras, dados dois eventos que estão separados no tempo, é possível encontrar um quadro no qual os dois eventos acontecem no mesmo lugar. Neste quadro, a separação no tempo, é chamada de tempo próprio .
- Δs 2 < 0: Neste caso, os dois eventos são separados por mais espaço do que tempo e, portanto, são considerados separados por espaço . Isso implica que e dada a transformação de Lorentz existe um menor que para o qual (em particular, ). Em outras palavras, dados dois eventos separados como no espaço, é possível encontrar um quadro no qual os dois eventos ocorram ao mesmo tempo. Nesse quadro, a separação no espaço é chamada de distância própria , ou comprimento próprio . Para valores maiores que e menores que o sinal de mudanças, significa que a ordem temporal de eventos separados por espaço muda dependendo do quadro em que os eventos são vistos. A ordem temporal de eventos separados no tempo, no entanto, é absoluta, uma vez que a única maneira que poderia ser maior do que seria se
- Δs 2 = 0: Neste caso, diz-se que os dois eventos são separados como luz . Isso implica que e essa relação é independente do referencial devido à invariância de A partir disso, observamos que a velocidade da luz está em todo referencial inercial. Em outras palavras, partindo da suposição da covariância universal de Lorentz, a velocidade constante da luz é um resultado derivado, e não um postulado como na formulação de dois postulados da teoria especial.
Relatividade de simultaneidade

Considere dois eventos acontecendo em dois locais diferentes que ocorrem simultaneamente no referencial de um observador inercial. Podem ocorrer de forma não simultânea no referencial de outro observador inercial (falta de simultaneidade absoluta ).
Da Equação 3 (a transformação direta de Lorentz em termos de diferenças de coordenadas)
É claro que os dois eventos que são simultâneos no referencial S (satisfazendo Δ t = 0 ), não são necessariamente simultâneos em outro referencial inercial S ′ (satisfazendo Δ t ′ = 0 ). Somente se esses eventos forem adicionalmente co-locais no quadro S (satisfazendo Δ x = 0 ), eles serão simultâneos em outro quadro S ′.
O efeito Sagnac pode ser considerado uma manifestação da relatividade da simultaneidade. Como a relatividade de simultaneidade é um efeito de primeira ordem em , instrumentos baseados no efeito Sagnac para sua operação, como giroscópios a laser de anel e giroscópios de fibra óptica , são capazes de níveis extremos de sensibilidade.
Dilatação do tempo
O lapso de tempo entre dois eventos não é invariante de um observador para outro, mas depende das velocidades relativas dos referenciais dos observadores (por exemplo, o paradoxo do gêmeo que diz respeito a um gêmeo que voa em uma nave espacial viajando próximo à velocidade da luz e retorna para descobrir que o irmão gêmeo que não viaja envelheceu muito mais, o paradoxo é que em velocidade constante somos incapazes de discernir qual gêmeo não viaja e qual gêmeo viaja).
Suponha que um relógio esteja em repouso no sistema sem primer S. A localização do relógio em dois ticks diferentes é então caracterizada por Δ x = 0 . Para encontrar a relação entre os tempos entre esses ticks medidos em ambos os sistemas, a Equação 3 pode ser usada para encontrar:
- para eventos satisfatórios
Isso mostra que o tempo (Δ t ′) entre os dois tiques, como visto no quadro em que o relógio está se movendo ( S ′), é maior do que o tempo (Δ t ) entre esses tiques, medido no quadro de descanso do relógio ( S ). A dilatação do tempo explica vários fenômenos físicos; por exemplo, o tempo de vida de múons de alta velocidade criados pela colisão de raios cósmicos com partículas na atmosfera externa da Terra e movendo-se em direção à superfície é maior do que o tempo de vida de múons de movimento lento, criados e decaindo em laboratório.
Contração do comprimento
As dimensões (por exemplo, comprimento) de um objeto medido por um observador podem ser menores do que os resultados das medições do mesmo objeto feitas por outro observador (por exemplo, o paradoxo da escada envolve uma longa escada viajando perto da velocidade da luz e sendo contida dentro de uma garagem menor).
Da mesma forma, suponha que uma barra de medição esteja em repouso e alinhada ao longo do eixo x no sistema sem primer S . Neste sistema, o comprimento desta haste é escrito como Δ x . Para medir o comprimento desta haste no sistema S ', no qual a haste está se movendo, as distâncias x ' até os pontos extremos da haste devem ser medidas simultaneamente nesse sistema S '. Em outras palavras, a medida é caracterizada por Δ t ′ = 0 , que pode ser combinada com a Equação 4 para encontrar a relação entre os comprimentos Δ x e Δ x ′:
- para eventos satisfatórios
Isso mostra que o comprimento (Δ x ′) da haste medido no quadro em que está se movendo ( S ′ ) é menor que seu comprimento (Δ x ) em seu próprio quadro de repouso ( S ).
A dilatação do tempo e a contração do comprimento não são meras aparências. A dilatação do tempo está explicitamente relacionada à nossa maneira de medir intervalos de tempo entre eventos que ocorrem no mesmo local em um determinado sistema de coordenadas (chamados eventos "co-locais"). Esses intervalos de tempo (que podem ser, e são, na verdade medidos experimentalmente por observadores relevantes) são diferentes em outro sistema de coordenadas movendo-se em relação ao primeiro, a menos que os eventos, além de co-locais, também sejam simultâneos. Da mesma forma, a contração do comprimento está relacionada às nossas distâncias medidas entre eventos separados, mas simultâneos, em um determinado sistema de coordenadas de escolha. Se esses eventos não forem co-locais, mas estiverem separados por distância (espaço), eles não ocorrerão na mesma distância espacial um do outro quando vistos de outro sistema de coordenadas em movimento.
Transformação de Lorentz de velocidades
Considere dois quadros S e S′ na configuração padrão. Uma partícula em S se move na direção x com vetor velocidade Qual é sua velocidade no referencial S' ?
Nós podemos escrever
|
|
|
( 7 ) |
|
|
|
( 8 ) |
A substituição de expressões para e da Equação 5 na Equação 8 , seguida por manipulações matemáticas diretas e substituição reversa da Equação 7 produz a transformação de Lorentz da velocidade para :
|
|
|
( 9 ) |
A relação inversa é obtida trocando os símbolos primos e não primos e substituindo por
|
|
|
( 10 ) |
Para não alinhado ao longo do eixo x, escrevemos:
|
|
|
( 11 ) |
|
|
|
( 12 ) |
As transformações direta e inversa para este caso são:
|
|
|
( 13 ) |
|
|
|
( 14 ) |
A Equação 10 e a Equação 14 podem ser interpretadas como dando a resultante das duas velocidadesesubstituem a fórmulaque é válida na relatividade galileana. Interpretadas dessa forma, elas são comumente chamadas de fórmulas de adição (ou composição) de velocidade relativística , válidas para os três eixos de S e S′ estarem alinhados entre si (embora não necessariamente na configuração padrão).
Observamos os seguintes pontos:
- Se um objeto (por exemplo, um fóton ) estivesse se movendo na velocidade da luz em um quadro (ou seja, u = ± c ou u′ = ± c ), então ele também estaria se movendo na velocidade da luz em qualquer outro quadro, movendo-se em | v | < c .
- A velocidade resultante de duas velocidades com módulo menor que c é sempre uma velocidade com módulo menor que c .
- Se ambos | você | e | v | (e então também | u′ | e | v′ |) são pequenos em relação à velocidade da luz (isto é, por exemplo, | você/c| ≪ 1 ), então as transformações intuitivas de Galileu são recuperadas das equações de transformação para a relatividade especial
- Anexar um quadro a um fóton ( montando um feixe de luz como Einstein considera) requer um tratamento especial das transformações.
Não há nada de especial na direção x na configuração padrão. O formalismo acima se aplica a qualquer direção; e três direções ortogonais permitem lidar com todas as direções no espaço decompondo os vetores velocidade em seus componentes nessas direções. Consulte Fórmula de adição de velocidade para obter detalhes.
Rotação de Thomas
A composição de dois boosts de Lorentz não colineares (ou seja, duas transformações de Lorentz não colineares, nenhuma das quais envolve rotação) resulta em uma transformação de Lorentz que não é um boost puro, mas é a composição de um boost e uma rotação.
A rotação de Thomas resulta da relatividade da simultaneidade. Na Fig. 4-2a, uma haste de comprimento em sua estrutura de repouso (isto é, com um comprimento adequado de ) sobe verticalmente ao longo do eixo y na estrutura de solo.
Na Fig. 4-2b, a mesma haste é observada do referencial de um foguete movendo-se com velocidade para a direita. Se imaginarmos dois relógios situados nas extremidades esquerda e direita da haste que estão sincronizados no quadro da haste, a relatividade da simultaneidade faz com que o observador no quadro do foguete observe (não veja ) o relógio na extremidade direita da haste como sendo avançado no tempo e a haste é correspondentemente observada como inclinada.
Ao contrário dos efeitos relativísticos de segunda ordem, como contração do comprimento ou dilatação do tempo, esse efeito se torna bastante significativo mesmo em velocidades bastante baixas. Por exemplo, isso pode ser visto no spin de partículas em movimento , onde a precessão de Thomas é uma correção relativista que se aplica ao spin de uma partícula elementar ou à rotação de um giroscópio macroscópico , relacionando a velocidade angular do spin de uma partícula seguindo um órbita curvilínea à velocidade angular do movimento orbital.
A rotação de Thomas fornece a resolução para o conhecido "paradoxo do medidor e do buraco".
Causalidade e proibição de movimento mais rápido que a luz

Na Fig. 4-3, o intervalo de tempo entre os eventos A (a "causa") e B (o "efeito") é 'semelhante ao tempo'; isto é, existe um quadro de referência no qual os eventos A e B ocorrem no mesmo local no espaço , separados apenas por ocorrerem em tempos diferentes. Se A precede B nesse quadro, então A precede B em todos os quadros acessíveis por uma transformação de Lorentz. É possível que a matéria (ou informação) viaje (abaixo da velocidade da luz) do local de A, começando no momento de A, até o local de B, chegando no momento de B, de modo que pode haver uma relação causal ( sendo A a causa e B o efeito).
O intervalo AC no diagrama é 'semelhante ao espaço'; ou seja, há um referencial no qual os eventos A e C ocorrem simultaneamente, separados apenas no espaço. Há também quadros em que A precede C (como mostrado) e quadros em que C precede A. No entanto, não há quadros acessíveis por uma transformação de Lorentz, em que os eventos A e C ocorrem no mesmo local. Se fosse possível existir uma relação de causa e efeito entre os eventos A e C, então surgiriam paradoxos de causalidade.
Por exemplo, se os sinais pudessem ser enviados mais rápido que a luz, então os sinais poderiam ser enviados para o passado do emissor (observador B nos diagramas). Uma variedade de paradoxos causais poderia então ser construída.
Considere os diagramas de espaço-tempo na Fig. 4-4. A e B estão ao lado de uma linha férrea, quando um trem de alta velocidade passa, com C no último vagão do trem e D no vagão da frente. As linhas do mundo de A e B são verticais ( ct ), distinguindo a posição estacionária desses observadores no solo, enquanto as linhas do mundo de C e D são inclinadas para frente ( ct′ ), refletindo o movimento rápido dos observadores C e D parados em seu trem, observados do solo.
- Fig. 4-4a. O evento "B passando uma mensagem para D", quando o carro da frente passa, está na origem do quadro de D. D envia a mensagem ao longo do trem para C no vagão traseiro, usando um "comunicador instantâneo" fictício. A linha de mundo desta mensagem é a seta vermelha gorda ao longo do eixo, que é uma linha de simultaneidade nos quadros preparados de C e D. No quadro de terra (sem preparação), o sinal chega mais cedo do que foi enviado.
- Fig. 4-4b. O evento de "C passando a mensagem para A", que está de pé junto aos trilhos da ferrovia, está na origem de seus quadros. Agora A envia a mensagem ao longo das trilhas para B através de um "comunicador instantâneo". A linha de mundo desta mensagem é a seta azul gorda, ao longo do eixo, que é uma linha de simultaneidade para os quadros de A e B. Como visto no diagrama de espaço-tempo, B receberá a mensagem antes de enviá-la, uma violação de causalidade.
Não é necessário que os sinais sejam instantâneos para violar a causalidade. Mesmo que o sinal de D para C fosse um pouco mais raso que o eixo (e o sinal de A para B um pouco mais inclinado que o eixo), ainda seria possível para B receber sua mensagem antes de enviá-la. Ao aumentar a velocidade do trem para velocidades próximas da luz, os eixos e podem ser espremidos muito perto da linha tracejada que representa a velocidade da luz. Com esta configuração modificada, pode ser demonstrado que mesmo sinais apenas ligeiramente mais rápidos que a velocidade da luz resultarão em violação de causalidade.
Portanto, se a causalidade deve ser preservada, uma das consequências da relatividade especial é que nenhum sinal de informação ou objeto material pode viajar mais rápido que a luz no vácuo.
Isso não quer dizer que todas as velocidades mais rápidas que a da luz sejam impossíveis. Várias situações triviais podem ser descritas onde algumas "coisas" (não matéria ou energia reais) se movem mais rápido que a luz. Por exemplo, o local onde o feixe de uma luz de busca atinge o fundo de uma nuvem pode se mover mais rápido que a luz quando a luz de busca é ligada rapidamente (embora isso não viole a causalidade ou qualquer outro fenômeno relativista).
Efeitos ópticos
Efeitos de arrastar
Em 1850, Hippolyte Fizeau e Léon Foucault estabeleceram independentemente que a luz viaja mais lentamente na água do que no ar, validando assim uma previsão da teoria ondulatória da luz de Fresnel e invalidando a previsão correspondente da teoria corpuscular de Newton . A velocidade da luz foi medida em água parada. Qual seria a velocidade da luz na água corrente?
Em 1851, Fizeau realizou um experimento para responder a essa pergunta, cuja representação simplificada está ilustrada na Figura 5-1. Um feixe de luz é dividido por um divisor de feixe, e os feixes divididos são passados em direções opostas através de um tubo de água corrente. Eles são recombinados para formar franjas de interferência, indicando uma diferença no comprimento do caminho óptico, que um observador pode ver. O experimento demonstrou que o arrasto da luz pela água corrente causava um deslocamento das franjas, mostrando que o movimento da água havia afetado a velocidade da luz.
De acordo com as teorias prevalecentes na época, a luz viajando através de um meio em movimento seria uma simples soma de sua velocidade através do meio mais a velocidade do meio. Ao contrário da expectativa, Fizeau descobriu que, embora a luz parecesse ser arrastada pela água, a magnitude do arrasto era muito menor do que o esperado. Se é a velocidade da luz na água parada, e é a velocidade da água, e é a velocidade da luz na água no quadro do laboratório com o fluxo de água somando ou subtraindo a velocidade da luz, então
Os resultados de Fizeau, embora consistentes com a hipótese anterior de Fresnel de arrastamento parcial do éter , foram extremamente desconcertantes para os físicos da época. Entre outras coisas, a presença de um termo de índice de refração significava que, como depende do comprimento de onda, o éter deve ser capaz de sustentar diferentes movimentos ao mesmo tempo. Uma variedade de explicações teóricas foram propostas para explicar o coeficiente de arrasto de Fresnel que estavam completamente em desacordo entre si. Mesmo antes do experimento de Michelson-Morley , os resultados experimentais de Fizeau estavam entre uma série de observações que criaram uma situação crítica para explicar a ótica dos corpos em movimento.
Do ponto de vista da relatividade especial, o resultado de Fizeau nada mais é do que uma aproximação da Equação 10 , a fórmula relativística para composição de velocidades.
Aberração relativística da luz
Por causa da velocidade finita da luz, se os movimentos relativos de uma fonte e receptor incluem um componente transversal, então a direção da qual a luz chega ao receptor será deslocada da posição geométrica no espaço da fonte em relação ao receptor. O cálculo clássico do deslocamento assume duas formas e faz previsões diferentes dependendo se o receptor, a fonte ou ambos estão em movimento em relação ao meio. (1) Se o receptor estiver em movimento, o deslocamento seria consequência da aberração da luz . O ângulo de incidência do feixe em relação ao receptor seria calculável a partir da soma vetorial dos movimentos do receptor e da velocidade da luz incidente. (2) Se a fonte estiver em movimento, o deslocamento seria consequência da correção luz-tempo . O deslocamento da posição aparente da fonte de sua posição geométrica seria o resultado do movimento da fonte durante o tempo que sua luz leva para chegar ao receptor.
A explicação clássica falhou no teste experimental. Como o ângulo de aberração depende da relação entre a velocidade do receptor e a velocidade da luz incidente, a passagem da luz incidente através de um meio refrativo deve alterar o ângulo de aberração. Em 1810, Arago usou esse fenômeno esperado em uma tentativa fracassada de medir a velocidade da luz e, em 1870, George Airy testou a hipótese usando um telescópio cheio de água, descobrindo que, contra a expectativa, a aberração medida era idêntica à aberração medida. com um telescópio cheio de ar. Uma tentativa "embaraçosa" de explicar esses resultados usou a hipótese de arrasto de éter parcial, mas foi incompatível com os resultados do experimento de Michelson-Morley , que aparentemente exigia arrasto de éter completo .
Assumindo referenciais inerciais, a expressão relativística para a aberração da luz é aplicável tanto para os casos de movimentação do receptor quanto da movimentação da fonte. Uma variedade de fórmulas trigonométricas equivalentes foram publicadas. Expresso em termos das variáveis na Fig. 5-2, elas incluem
- OU OU
Efeito Doppler Relativístico
Efeito Doppler longitudinal relativístico
O efeito Doppler clássico depende se a fonte, o receptor ou ambos estão em movimento em relação ao meio. O efeito Doppler relativístico é independente de qualquer meio. No entanto, o deslocamento Doppler relativístico para o caso longitudinal, com fonte e receptor movendo-se diretamente em direção ou para longe um do outro, pode ser derivado como se fosse o fenômeno clássico, mas modificado pela adição de um termo de dilatação do tempo , e esse é o tratamento descrito aqui.
Suponha que o receptor e a fonte estejam se afastando um do outro com uma velocidade relativa medida por um observador no receptor ou na fonte (a convenção de sinal adotada aqui é negativa se o receptor e a fonte estiverem se movendo um em direção ao outro). Suponha que a fonte esteja estacionária no meio. Então
Para a luz, e com o receptor se movendo em velocidades relativísticas, os relógios no receptor são dilatados no tempo em relação aos relógios na fonte. O receptor medirá a frequência recebida a ser
- e
- é o fator de Lorentz .
Uma expressão idêntica para o deslocamento Doppler relativístico é obtida ao realizar a análise no quadro de referência do receptor com uma fonte em movimento.
Efeito Doppler Transversal
O efeito Doppler transversal é uma das principais novas previsões da teoria da relatividade especial.
Classicamente, pode-se esperar que, se a fonte e o receptor estiverem se movendo transversalmente um em relação ao outro, sem componente longitudinal para seus movimentos relativos, não haverá deslocamento Doppler na luz que chega ao receptor.
A relatividade especial prevê o contrário. A Fig. 5-3 ilustra duas variantes comuns desse cenário. Ambas as variantes podem ser analisadas usando argumentos simples de dilatação do tempo. Na Fig. 5-3a, o receptor observa a luz da fonte como sendo desviada para o azul por um fator de . Na Fig. 5-3b, a luz é desviada para o vermelho pelo mesmo fator.
Medição versus aparência visual
A dilatação do tempo e a contração do comprimento não são ilusões de ótica, mas efeitos genuínos. As medições desses efeitos não são um artefato do deslocamento Doppler , nem são o resultado da negligência em levar em conta o tempo que a luz leva para viajar de um evento para um observador.
Os cientistas fazem uma distinção fundamental entre medição ou observação , por um lado, versus aparência visual , ou o que se vê . A forma medida de um objeto é um instantâneo hipotético de todos os pontos do objeto como eles existem em um único momento no tempo. A aparência visual de um objeto, no entanto, é afetada pela variação de tempo que a luz leva para viajar de diferentes pontos do objeto até o olho.
Por muitos anos, a distinção entre os dois não foi geralmente apreciada, e geralmente se pensava que um objeto de comprimento contraído passando por um observador seria de fato visto como comprimento contraído. Em 1959, James Terrell e Roger Penrose apontaram independentemente que os efeitos de atraso de tempo diferencial em sinais que chegam ao observador de diferentes partes de um objeto em movimento resultam em uma aparência visual de um objeto em movimento rápido sendo bastante diferente de sua forma medida. Por exemplo, um objeto que se afasta parece contraído, um objeto que se aproxima parece alongado e um objeto que passa teria uma aparência inclinada que foi comparada a uma rotação. Uma esfera em movimento mantém o contorno circular, embora a superfície da esfera e as imagens nela apareçam distorcidas.

A Fig. 5-4 ilustra um cubo visto a uma distância de quatro vezes o comprimento de seus lados. Em altas velocidades, os lados do cubo que são perpendiculares à direção do movimento parecem hiperbólicos. O cubo na verdade não é girado. Em vez disso, a luz da parte traseira do cubo leva mais tempo para atingir os olhos em comparação com a luz da frente, durante o qual o cubo se moveu para a direita. Essa ilusão ficou conhecida como rotação Terrell ou efeito Terrell-Penrose .
Outro exemplo em que a aparência visual está em desacordo com a medição vem da observação do movimento superluminal aparente em várias galáxias de rádio , objetos BL Lac , quasares e outros objetos astronômicos que ejetam jatos de matéria de velocidade relativística em ângulos estreitos em relação ao observador. Uma aparente ilusão de ótica resulta dando a aparência de uma viagem mais rápida que a luz. Na Fig. 5-5, a galáxia M87 emite um jato de partículas subatômicas em alta velocidade quase diretamente em nossa direção, mas a rotação de Penrose-Terrell faz com que o jato pareça estar se movendo lateralmente da mesma maneira que a aparência do cubo na Fig . 5-5. 5-4 foi estendido.
Dinâmica
A seção Consequências derivadas da transformação de Lorentz tratou estritamente da cinemática , o estudo do movimento de pontos, corpos e sistemas de corpos sem considerar as forças que causaram o movimento. Esta seção discute massas, forças, energia e assim por diante e, como tal, requer a consideração de efeitos físicos além daqueles englobados pela própria transformação de Lorentz.
Equivalência de massa e energia
À medida que a velocidade de um objeto se aproxima da velocidade da luz do ponto de vista de um observador, sua massa relativística aumenta, tornando cada vez mais difícil acelerá-lo a partir do referencial do observador.
O conteúdo de energia de um objeto em repouso com massa m é igual a mc 2 . A conservação de energia implica que, em qualquer reação, uma diminuição da soma das massas das partículas deve ser acompanhada por um aumento nas energias cinéticas das partículas após a reação. Da mesma forma, a massa de um objeto pode ser aumentada absorvendo energias cinéticas.
Além dos artigos mencionados acima – que fornecem derivações da transformação de Lorentz e descrevem os fundamentos da relatividade especial – Einstein também escreveu pelo menos quatro artigos dando argumentos heurísticos para a equivalência (e transmutabilidade) de massa e energia, para E = mc 2 .
A equivalência massa-energia é uma consequência da relatividade especial. A energia e o momento, que são separados na mecânica newtoniana, formam um quatro vetores na relatividade, e isso relaciona o componente do tempo (a energia) aos componentes do espaço (o momento) de uma maneira não trivial. Para um objeto em repouso, o quatro vetor energia-momento é ( E / c , 0, 0, 0) : ele tem um componente de tempo que é a energia e três componentes de espaço que são zero. Ao mudar os quadros com uma transformação de Lorentz na direção x com um pequeno valor da velocidade v, o quatro vetores do momento de energia se torna ( E / c , Ev / c 2 , 0, 0) . O momento é igual à energia multiplicada pela velocidade dividida por c 2 . Como tal, a massa newtoniana de um objeto, que é a razão entre o momento e a velocidade para velocidades lentas, é igual a E / c 2 .
A energia e o momento são propriedades da matéria e da radiação, e é impossível deduzir que eles formam um quatro vetor apenas a partir dos dois postulados básicos da relatividade especial por si mesmos, porque estes não falam sobre matéria ou radiação, eles apenas falam sobre espaço e tempo. A derivação, portanto, requer algum raciocínio físico adicional. Em seu artigo de 1905, Einstein usou os princípios adicionais que a mecânica newtoniana deve manter para velocidades lentas, de modo que haja uma energia escalar e um momento de três vetores em velocidades lentas, e que a lei de conservação para energia e momento seja exatamente verdadeira na relatividade. . Além disso, ele assumiu que a energia da luz é transformada pelo mesmo fator de deslocamento Doppler que sua frequência, o que ele havia demonstrado anteriormente com base nas equações de Maxwell. O primeiro dos artigos de Einstein sobre esse assunto foi "A inércia de um corpo depende de seu conteúdo de energia?" em 1905. Embora o argumento de Einstein neste artigo seja quase universalmente aceito pelos físicos como correto, até mesmo evidente, muitos autores ao longo dos anos sugeriram que ele está errado. Outros autores sugerem que o argumento foi meramente inconclusivo porque se baseou em algumas suposições implícitas.
Einstein reconheceu a controvérsia sobre sua derivação em seu trabalho de pesquisa de 1907 sobre a relatividade especial. Lá, ele observa que é problemático confiar nas equações de Maxwell para o argumento heurístico de massa-energia. O argumento em seu artigo de 1905 pode ser realizado com a emissão de quaisquer partículas sem massa, mas as equações de Maxwell são usadas implicitamente para tornar óbvio que a emissão de luz em particular só pode ser alcançada realizando trabalho. Para emitir ondas eletromagnéticas, tudo o que você precisa fazer é sacudir uma partícula carregada, e isso está claramente fazendo trabalho, de modo que a emissão é de energia.
A que distância se pode viajar da Terra?
Como não se pode viajar mais rápido que a luz, pode-se concluir que um humano nunca pode viajar mais longe da Terra do que 40 anos-luz se o viajante estiver ativo entre 20 e 60 anos. atingem mais do que os poucos sistemas solares que existem dentro do limite de 20 a 40 anos-luz da Terra. Mas essa seria uma conclusão equivocada. Por causa da dilatação do tempo, uma nave espacial hipotética pode viajar milhares de anos-luz durante os 40 anos ativos do piloto. Se uma nave espacial pudesse ser construída com uma aceleração constante de 1 g , ela estaria, depois de pouco menos de um ano, viajando quase à velocidade da luz vista da Terra. Isso é descrito por:
onde v ( t ) é a velocidade no instante t , a é a aceleração de 1 g e t é o tempo medido pelas pessoas na Terra. Portanto, após um ano de aceleração de 9,81 m/s 2 , a espaçonave estará viajando a v = 0,77 c em relação à Terra. A dilatação do tempo aumentará o tempo de vida do viajante visto do referencial da Terra para 2,7 anos, mas seu tempo de vida medido por um relógio viajando com ele não mudará. Durante sua jornada, as pessoas na Terra experimentarão mais tempo do que elas. Uma viagem de ida e volta de 5 anos para o viajante levará 6,5 anos terrestres e cobrirá uma distância de mais de 6 anos-luz. Uma viagem de ida e volta de 20 anos para eles (5 anos acelerando, 5 desacelerando, duas vezes cada) os levará de volta à Terra, tendo viajado por 335 anos terrestres e uma distância de 331 anos-luz. Uma viagem completa de 40 anos a 1 g aparecerá na Terra para durar 58.000 anos e cobrir uma distância de 55.000 anos-luz. Uma viagem de 40 anos a 1,1 g levará 148.000 anos terrestres e cobrirá cerca de 140.000 anos-luz. Uma viagem de ida de 28 anos (14 anos acelerando, 14 desacelerando conforme medido com o relógio do astronauta) com 1 g de aceleração poderia chegar a 2.000.000 anos-luz até a Galáxia de Andrômeda. Essa mesma dilatação de tempo é o motivo pelo qual um múon viajando próximo a c é observado viajando muito mais do que c vezes sua meia-vida (quando em repouso).
Relatividade e eletromagnetismo unificador
A investigação teórica no eletromagnetismo clássico levou à descoberta da propagação de ondas. Equações generalizando os efeitos eletromagnéticos descobriram que a velocidade de propagação finita dos campos E e B exigiam certos comportamentos em partículas carregadas. O estudo geral de cargas em movimento forma o potencial de Liénard-Wiechert , que é um passo em direção à relatividade especial.
A transformação de Lorentz do campo elétrico de uma carga em movimento no referencial de um observador imóvel resulta no aparecimento de um termo matemático comumente chamado de campo magnético . Por outro lado, o campo magnético gerado por uma carga em movimento desaparece e se torna um campo puramente eletrostático em um quadro de referência comovente. As equações de Maxwell são, portanto, simplesmente um ajuste empírico para efeitos relativísticos especiais em um modelo clássico do Universo. Como os campos elétrico e magnético são dependentes do referencial e, portanto, entrelaçados, fala-se de campos eletromagnéticos . A relatividade especial fornece as regras de transformação de como um campo eletromagnético em um referencial inercial aparece em outro referencial inercial.
As equações de Maxwell na forma 3D já são consistentes com o conteúdo físico da relatividade especial, embora sejam mais fáceis de manipular em uma forma manifestamente covariante , ou seja, na linguagem do cálculo tensorial .
Teorias da relatividade e mecânica quântica
A relatividade especial pode ser combinada com a mecânica quântica para formar a mecânica quântica relativística e a eletrodinâmica quântica . Como a relatividade geral e a mecânica quântica podem ser unificadas é um dos problemas não resolvidos da física ; gravidade quântica e uma " teoria de tudo ", que requerem uma unificação incluindo também a relatividade geral, são áreas ativas e em andamento na pesquisa teórica.
O modelo atômico inicial de Bohr-Sommerfeld explicou a estrutura fina dos átomos de metais alcalinos usando tanto a relatividade especial quanto o conhecimento preliminar da mecânica quântica da época.
Em 1928, Paul Dirac construiu uma influente equação de onda relativística , agora conhecida como equação de Dirac em sua homenagem, que é totalmente compatível tanto com a relatividade especial quanto com a versão final da teoria quântica existente após 1926. momento dos elétrons chamado spin , também levou à previsão da antipartícula do elétron (o pósitron ), e a estrutura fina só poderia ser totalmente explicada com relatividade especial. Foi o primeiro fundamento da mecânica quântica relativística .
Por outro lado, a existência de antipartículas leva à conclusão de que a mecânica quântica relativística não é suficiente para uma teoria mais precisa e completa das interações das partículas. Em vez disso, torna-se necessária uma teoria de partículas interpretadas como campos quantizados, chamada teoria quântica de campos ; em que partículas podem ser criadas e destruídas ao longo do espaço e do tempo.
Status
A relatividade especial em seu espaço-tempo Minkowski é precisa apenas quando o valor absoluto do potencial gravitacional é muito menor que c 2 na região de interesse. Em um campo gravitacional forte, deve-se usar a relatividade geral . A relatividade geral torna-se relatividade especial no limite de um campo fraco. Em escalas muito pequenas, como no comprimento de Planck e abaixo, os efeitos quânticos devem ser levados em consideração, resultando em gravidade quântica . No entanto, em escalas macroscópicas e na ausência de campos gravitacionais fortes, a relatividade especial é testada experimentalmente com um grau de precisão extremamente alto (10 −20 ) e, portanto, aceito pela comunidade física. Os resultados experimentais que parecem contradizê-lo não são reprodutíveis e, portanto, acredita-se amplamente que se devem a erros experimentais.
A relatividade especial é matematicamente auto-consistente e é uma parte orgânica de todas as teorias físicas modernas, mais notavelmente a teoria quântica de campos , a teoria das cordas e a relatividade geral (no caso limite de campos gravitacionais desprezíveis).
A mecânica newtoniana segue matematicamente da relatividade especial em pequenas velocidades (em comparação com a velocidade da luz) - assim, a mecânica newtoniana pode ser considerada como uma relatividade especial de corpos em movimento lento. Veja mecânica clássica para uma discussão mais detalhada.
Vários experimentos anteriores ao artigo de Einstein de 1905 são agora interpretados como evidência da relatividade. Destes, sabe-se que Einstein estava ciente do experimento de Fizeau antes de 1905, e os historiadores concluíram que Einstein estava pelo menos ciente do experimento de Michelson-Morley já em 1899, apesar das alegações que ele fez em seus últimos anos de que não desempenhou nenhum papel em seu desenvolvimento. desenvolvimento da teoria.
- O experimento de Fizeau (1851, repetido por Michelson e Morley em 1886) mediu a velocidade da luz em meios móveis, com resultados consistentes com a adição relativística de velocidades colineares.
- O famoso experimento de Michelson-Morley (1881, 1887) deu mais suporte ao postulado de que a detecção de uma velocidade de referência absoluta não era possível. Deve-se afirmar aqui que, ao contrário de muitas alegações alternativas, ele disse pouco sobre a invariância da velocidade da luz em relação à fonte e à velocidade do observador, já que tanto a fonte quanto o observador estavam viajando juntos na mesma velocidade o tempo todo.
- O experimento de Trouton-Noble (1903) mostrou que o torque em um capacitor é independente da posição e do referencial inercial.
- Os Experimentos de Rayleigh e Brace (1902, 1904) mostraram que a contração do comprimento não leva à birrefringência para um observador em movimento, de acordo com o princípio da relatividade.
Os aceleradores de partículas rotineiramente aceleram e medem as propriedades das partículas que se movem perto da velocidade da luz, onde seu comportamento é completamente consistente com a teoria da relatividade e inconsistente com a mecânica newtoniana anterior . Essas máquinas simplesmente não funcionariam se não fossem projetadas de acordo com princípios relativísticos. Além disso, um número considerável de experimentos modernos foi conduzido para testar a relatividade especial. Alguns exemplos:
- Testes de energia e momento relativísticos – testando a velocidade limite das partículas
- Experimento de Ives-Stilwell - testando efeito Doppler relativístico e dilatação do tempo
- Teste experimental de dilatação do tempo - efeitos relativísticos na meia-vida de uma partícula em movimento rápido
- Experimento Kennedy–Thorndike – dilatação do tempo de acordo com as transformações de Lorentz
- Experimento Hughes-Drever - testando a isotropia do espaço e da massa
- Pesquisas modernas por violação de Lorentz – vários testes modernos
- Experimentos para testar a teoria da emissão demonstraram que a velocidade da luz é independente da velocidade do emissor.
- Experimentos para testar a hipótese de arrasto do éter - sem "obstrução do fluxo do éter".
Discussão técnica do espaço-tempo
Geometria do espaço-tempo
Comparação entre o espaço euclidiano plano e o espaço de Minkowski

A relatividade especial usa um espaço 'plano' de Minkowski de 4 dimensões – um exemplo de espaço -tempo . O espaço-tempo de Minkowski parece ser muito semelhante ao espaço euclidiano tridimensional padrão , mas há uma diferença crucial em relação ao tempo.
No espaço 3D, o diferencial de distância (elemento de linha) ds é definido por
onde d x = ( dx 1 , dx 2 , dx 3 ) são os diferenciais das três dimensões espaciais. Na geometria de Minkowski, há uma dimensão extra com coordenada X 0 derivada do tempo, tal que o diferencial de distância cumpre
onde dX = ( dX 0 , dX 1 , dX 2 , dX 3 ) são os diferenciais das quatro dimensões do espaço-tempo . Isso sugere um profundo insight teórico: a relatividade especial é simplesmente uma simetria rotacional do nosso espaço-tempo, análoga à simetria rotacional do espaço euclidiano (veja a Fig. 10-1). Assim como o espaço euclidiano usa uma métrica euclidiana , o espaço-tempo usa uma métrica Minkowski .Basicamente, a relatividade especial pode ser definida como a invariância de qualquer intervalo de espaço-tempo (que é a distância 4D entre quaisquer dois eventos) quando vista de qualquer referencial inercial . Todas as equações e efeitos da relatividade especial podem ser derivados dessa simetria rotacional (o grupo de Poincaré ) do espaço-tempo de Minkowski.
A forma real de ds acima depende da métrica e das escolhas para a coordenada X 0 . Para fazer a coordenada de tempo parecer com as coordenadas do espaço, ela pode ser tratada como imaginária : X 0 = ict (isso é chamado de rotação Wick ). De acordo com Misner, Thorne e Wheeler (1971, §2.3), em última análise, a compreensão mais profunda da relatividade especial e geral virá do estudo da métrica de Minkowski (descrita abaixo) e tomar X 0 = ct , em vez de um "disfarçado " Métrica euclidiana usando ict como coordenada de tempo.
Alguns autores usam X 0 = t , com fatores de c em outros lugares para compensar; por exemplo, as coordenadas espaciais são divididas por c ou fatores de c ±2 são incluídos no tensor métrico. Essas numerosas convenções podem ser substituídas usando unidades naturais onde c = 1 . Então espaço e tempo têm unidades equivalentes e nenhum fator de c aparece em qualquer lugar.
espaço-tempo 3D
Se reduzirmos as dimensões espaciais para 2, para que possamos representar a física em um espaço 3D
vemos que as geodésicas nulas se encontram ao longo de um cone duplo (veja a Fig. 10-2) definido pela equação;
ou simplesmente
que é a equação de um círculo de raio c dt .
espaço-tempo 4D
Se estendermos isso para três dimensões espaciais, as geodésicas nulas são o cone de 4 dimensões:
assim
Conforme ilustrado na Fig. 10-3, as geodésicas nulas podem ser visualizadas como um conjunto de esferas concêntricas contínuas com raios = c dt .
Este dual-cone nulo representa a "linha de visão" de um ponto no espaço. Ou seja, quando olhamos para as estrelas e dizemos "A luz daquela estrela que estou recebendo tem X anos", estamos olhando para esta linha de visão: uma geodésica nula. Estamos olhando para um evento distante e um tempo d/c no passado. Por esta razão, o cone dual nulo também é conhecido como 'cone de luz'. (O ponto no canto inferior esquerdo da Fig. 10-2 representa a estrela, a origem representa o observador e a linha representa a "linha de visão" geodésica nula.)
O cone na região −t é a informação que o ponto está 'recebendo', enquanto o cone na seção + t é a informação que o ponto está 'enviando'.
A geometria do espaço de Minkowski pode ser representada usando diagramas de Minkowski , que também são úteis para entender muitos dos experimentos mentais em relatividade especial.
Observe que, no espaço-tempo 4d, o conceito de centro de massa fica mais complicado, veja Centro de massa (relativístico) .
Física no espaço-tempo
Transformações de grandezas físicas entre referenciais
Acima, a transformação de Lorentz para a coordenada de tempo e três coordenadas de espaço ilustra que elas estão entrelaçadas. Isso é verdade de maneira mais geral: certos pares de quantidades "semelhantes ao tempo" e "semelhantes ao espaço" combinam-se naturalmente em pé de igualdade sob a mesma transformação de Lorentz.
A transformação de Lorentz na configuração padrão acima, ou seja, para um impulso na direção x , pode ser reformulada em forma de matriz da seguinte forma:
Na mecânica newtoniana, as quantidades que possuem magnitude e direção são matematicamente descritas como vetores 3d no espaço euclidiano e, em geral, são parametrizadas pelo tempo. Na relatividade especial, essa noção é estendida adicionando a quantidade apropriada do tipo tempo a uma quantidade vetorial tipo espaço, e temos vetores 4d, ou " quatro vetores ", no espaço-tempo de Minkowski. Os componentes de vetores são escritos usando notação de índice tensorial , pois isso tem inúmeras vantagens. A notação deixa claro que as equações são manifestamente covariantes sob o grupo de Poincaré , contornando assim os cálculos tediosos para verificar esse fato. Ao construir tais equações, muitas vezes descobrimos que as equações anteriormente consideradas não relacionadas são, de fato, intimamente conectadas, sendo parte da mesma equação tensorial. Reconhecer outras quantidades físicas como tensores simplifica suas leis de transformação. Em toda parte, os índices superiores (sobrescritos) são índices contravariantes em vez de expoentes, exceto quando indicam um quadrado (isso deve ficar claro no contexto), e os índices inferiores (subscritos) são índices covariantes. Por simplicidade e consistência com as equações anteriores, serão usadas coordenadas cartesianas.
O exemplo mais simples de um quatro-vetor é a posição de um evento no espaço-tempo, que constitui um componente tipo-tempo ct e componente tipo-espaço x = ( x , y , z ) , em um vetor de posição contravariante com componentes:
onde há uma soma implícita de 0 a 3, e é uma matriz .
Mais geralmente, todos os componentes contravariantes de uma transformação de quatro vetores de um quadro para outro quadro por uma transformação de Lorentz :
Exemplos de outros 4-vetores incluem a 4-velocidade definida como a derivada do 4-vetor de posição em relação ao tempo adequado :
A energia relativística e o momento relativístico de um objeto são, respectivamente, os componentes temporal e espacial de um vetor de quatro momentos contravariantes :
A aceleração de quatro é a derivada de tempo adequada de 4 velocidades:
As regras de transformação para velocidades e acelerações tridimensionais são muito complicadas ; mesmo acima, na configuração padrão, as equações de velocidade são bastante complicadas devido à sua não linearidade. Por outro lado, as transformações de quatro velocidades e quatro acelerações são mais simples por meio da matriz de transformação de Lorentz.
O gradiente de quatro de um campo escalar φ se transforma de forma covariante em vez de contravariante:
que é a transposição de:
apenas em coordenadas cartesianas. É a derivada covariante que se transforma em covariância manifesta, em coordenadas cartesianas isso se reduz às derivadas parciais, mas não em outras coordenadas.
Mais geralmente, os componentes covariantes de uma transformação de 4 vetores de acordo com a transformação inversa de Lorentz:
Os postulados da relatividade especial restringem a forma exata que as matrizes de transformação de Lorentz assumem.
Mais geralmente, a maioria das quantidades físicas são melhor descritas como (componentes de) tensores . Então, para transformar de um quadro para outro, usamos a conhecida lei de transformação tensorial
Um exemplo de tensor antissimétrico quadridimensional de segunda ordem é o momento angular relativístico , que possui seis componentes: três são o momento angular clássico e os outros três estão relacionados ao impulso do centro de massa do sistema. A derivada do momento angular relativístico em relação ao tempo próprio é o torque relativístico, também tensor antisimétrico de segunda ordem .
O tensor de campo eletromagnético é outro campo tensor antisimétrico de segunda ordem , com seis componentes: três para o campo elétrico e outros três para o campo magnético . Há também o tensor tensão-energia para o campo eletromagnético, ou seja, o tensor tensão-energia eletromagnética .
Métrica
O tensor métrico permite definir o produto interno de dois vetores, que por sua vez permite atribuir uma magnitude ao vetor. Dada a natureza quadridimensional do espaço-tempo, a métrica de Minkowski η tem componentes (válidos com coordenadas adequadamente escolhidas) que podem ser organizados em uma matriz 4 × 4 :
O grupo de Poincaré é o grupo mais geral de transformações que preserva a métrica de Minkowski:
e esta é a simetria física subjacente à relatividade especial.
A métrica pode ser usada para aumentar e diminuir índices em vetores e tensores. Invariantes podem ser construídos usando a métrica, o produto interno de um 4 vetor T com outro 4 vetor S é:
Invariante significa que assume o mesmo valor em todos os referenciais inerciais, porque é um escalar (tensor de posto 0), e assim nenhum Λ aparece em sua transformação trivial. A magnitude do 4-vetor T é a raiz quadrada positiva do produto interno consigo mesmo:
Pode-se estender essa ideia para tensores de ordem superior, para um tensor de segunda ordem podemos formar os invariantes:
Cinemática Relativística e Invariância
Os diferenciais de coordenadas também se transformam de forma contravariante:
A 4 velocidades U μ tem uma forma invariante:
Dinâmica relativística e invariância
A magnitude invariante do vetor momento 4 gera a relação energia-momento :
Podemos descobrir o que é esse invariante primeiro argumentando que, como é um escalar, não importa em qual referencial o calculamos e, em seguida, transformando para um referencial onde o momento total é zero.
Vemos que a energia de repouso é uma invariante independente. Uma energia de repouso pode ser calculada mesmo para partículas e sistemas em movimento, traduzindo para um referencial no qual o momento é zero.
A energia de repouso está relacionada com a massa de acordo com a célebre equação discutida acima:
A massa dos sistemas medida em seu centro do referencial de momento (onde o momento total é zero) é dada pela energia total do sistema neste referencial. Pode não ser igual à soma das massas individuais do sistema medidas em outros quadros.
Para usar a terceira lei do movimento de Newton , ambas as forças devem ser definidas como a taxa de variação do momento em relação à mesma coordenada de tempo. Ou seja, requer a força 3D definida acima. Infelizmente, não há tensor em 4D que contenha os componentes do vetor de força 3D entre seus componentes.
Se uma partícula não estiver viajando em c , pode-se transformar a força 3D do referencial em movimento da partícula no referencial do observador. Isso produz um vetor de 4, chamado de força de quatro . É a taxa de variação do quatro vetor de momento de energia acima em relação ao tempo adequado. A versão covariante da força de quatro é:
No quadro de repouso do objeto, o componente de tempo das quatro forças é zero, a menos que a " massa invariante " do objeto esteja mudando (isso requer um sistema não fechado no qual energia/massa está sendo adicionada ou removida diretamente do objeto ), caso em que é o negativo daquela taxa de variação de massa, vezes c . Em geral, porém, os componentes da força quatro não são iguais aos componentes da força três, porque a força três é definida pela taxa de variação do momento em relação ao tempo coordenado, ou seja, dp / dt enquanto o quatro força é definida pela taxa de variação do momento em relação ao tempo próprio, ou seja, dp / dτ .
Em um meio contínuo, a densidade de força 3D combina com a densidade de potência para formar um vetor de 4 covariantes. A parte espacial é o resultado da divisão da força em uma pequena célula (em 3 espaços) pelo volume dessa célula. A componente de tempo é -1/ c vezes a potência transferida para aquela célula dividida pelo volume da célula. Isso será usado abaixo na seção sobre eletromagnetismo.
Veja também
- Pessoas :
- Relatividade :
- Física :
- Matemática :
- Filosofia :
- Paradoxos :
Notas
Fontes primárias
Referências
Leitura adicional
Livros didáticos
- Einstein, Albert (1920). Relatividade: A Teoria Especial e Geral .
- Einstein, Albert (1996). O Significado da Relatividade . Belas Comunicações. ISBN 1-56731-136-9
- Logunov, Anatoly A. (2005). Henri Poincaré e a Teoria da Relatividade (tradução do russo por G. Pontocorvo e VO Soloviev, editado por VA Petrov). Nauka, Moscou.
- Charles Misner , Kip Thorne e John Archibald Wheeler (1971) Gravitação . WH Freeman & Co. ISBN 0-7167-0334-3
- Post, EJ, 1997 (1962) Formal Structure of Electromagnetics: General Covariance and Electromagnetics . Publicações Dover.
- Wolfgang Rindler (1991). Introdução à Relatividade Especial (2ª ed.), Oxford University Press. ISBN 978-0-19-853952-0 ; ISBN 0-19-853952-5
- Harvey R. Brown (2005). Relatividade física: estrutura espaço-tempo de uma perspectiva dinâmica, Oxford University Press, ISBN 0-19-927583-1 ; ISBN 978-0-19-927583-0
- Qadir, Asgar (1989). Relatividade: Uma Introdução à Teoria Especial . Cingapura: Publicações Científicas Mundiais . pág. 128. Bibcode : 1989rist.book.....Q . ISBN 978-9971-5-0612-4.
- Francês, AP (1968). Relatividade Especial (MIT Introductory Physics) (1ª ed.). WW Norton & Company. ISBN 978-0393097931.
- Silberstein, Ludwik (1914). A Teoria da Relatividade .
- Lawrence Sklar (1977). Espaço, Tempo e Espaço-tempo . Imprensa da Universidade da Califórnia. ISBN 978-0-520-03174-6.
- Lawrence Sklar (1992). Filosofia da Física . Imprensa Westview. ISBN 978-0-8133-0625-4.
- Sergey Stepanov (2018). Mundo Relativista . De Gruyter. ISBN 9783110515879.
- Taylor, Edwin e John Archibald Wheeler (1992). Física do espaço-tempo (2ª ed.). WH Freeman & Co. ISBN 0-7167-2327-1 .
- Tipler, Paul e Llewellyn, Ralph (2002). Física Moderna (4ª ed.). WH Freeman & Co. ISBN 0-7167-4345-0 .
artigos de jornal
- Alvager, T.; Farley, FJM; Kjellman, J.; Wallin, L.; et ai. (1964). "Teste do Segundo Postulado da Relatividade Especial na região GeV". Letras de Física . 12 (3): 260–262. Bibcode : 1964PhL....12..260A . doi : 10.1016/0031-9163(64)91095-9 .
- Darrigol, Oliver (2004). "O Mistério da Conexão Poincaré-Einstein". Ísis . 95 (4): 614–26. doi : 10.1086/430652 . PMID 16011297 . S2CID 26997100 .
- Lobo, Pedro; Petit, Geraldo (1997). "Teste de satélite de Relatividade Especial usando o Sistema de Posicionamento Global". Revisão Física A . 56 (6): 4405-09. Bibcode : 1997PhRvA..56.4405W . doi : 10.1103/PhysRevA.56.4405 .
- Relatividade Especial Scholarpedia
- Rindler, Wolfgang (2011). "Relatividade especial: Cinemática" . Scholarpedia . 6 (2): 8520. Bibcode : 2011SchpJ...6.8520R . doi : 10.4249/scholarpedia.8520 .
links externos
Obras originais
- Zur Elektrodynamik bewegter Körper Einstein's trabalho original em alemão, Annalen der Physik , Berna 1905
- Sobre a Eletrodinâmica dos Corpos em Movimento Tradução em inglês publicada no livro de 1923 The Principle of Relativity .
Relatividade especial para um público geral (não é necessário conhecimento matemático)
- Einstein Light Uma premiada introdução não técnica (clipes de filmes e demonstrações) apoiada por dezenas de páginas de explicações e animações adicionais, em níveis com ou sem matemática.
- Einstein Online Introdução à teoria da relatividade, do Instituto Max Planck de Física Gravitacional.
- Áudio: Caim/Gay (2006) – Elenco de Astronomia . A Teoria da Relatividade Especial de Einstein
Relatividade especial explicada (usando matemática simples ou mais avançada)
- Bondi K-Calculus – Uma introdução simples à teoria da relatividade especial.
- Fundações de Greg Egan .
- As Notas de Hogg sobre Relatividade Especial Uma boa introdução à relatividade especial no nível de graduação, usando cálculo.
- Calculadora de Relatividade: Relatividade Especial – Uma derivação de cálculo algébrico e integral para E = mc 2 .
- MathPages – Reflections on Relativity Um livro online completo sobre relatividade com uma extensa bibliografia.
- Relatividade Especial Uma introdução à relatividade especial no nível de graduação.
- Relatividade: a Teoria Especial e Geral no Projeto Gutenberg , deAlbert Einstein
- Notas de aula de relatividade especial é uma introdução padrão à relatividade especial contendo explicações ilustrativas baseadas em desenhos e diagramas de espaço-tempo do Instituto Politécnico da Virgínia e da Universidade Estadual.
- Entendendo a Relatividade Especial A teoria da relatividade especial de uma forma facilmente compreensível.
- An Introduction to the Special Theory of Relativity (1964) por Robert Katz, "uma introdução ... que é acessível a qualquer estudante que tenha tido uma introdução à física geral e alguma familiaridade com o cálculo" (130 pp; formato pdf) .
- Notas de Palestra sobre Relatividade Especial por JD Cresser Departamento de Física da Universidade Macquarie.
- SpecialRelativity.net – Uma visão geral com visualizações e matemática mínima.
- Relatividade 4-nunca? O problema do movimento superluminal é discutido de maneira divertida.
Visualização
- Software de Relatividade Especial de Raytracing que visualiza vários cenários sob a influência da relatividade especial.
- Relatividade em tempo real A Universidade Nacional Australiana. Efeitos visuais relativísticos experimentados através de um programa interativo.
- Viagem no espaço-tempo Uma variedade de visualizações de efeitos relativísticos, de movimento relativístico a buracos negros.
- Através dos olhos de Einstein A Universidade Nacional Australiana. Efeitos visuais relativísticos explicados com filmes e imagens.
- Warp Special Relativity Simulator Um programa de computador para mostrar os efeitos de viajar perto da velocidade da luz.
- Clipe de animação no YouTube visualizando a transformação de Lorentz.
- Animações FLASH interativas originais de John de Pillis ilustrando quadros de Lorentz e Galileu, Train and Tunnel Paradox, Twin Paradox, Wave Propagation, Clock Synchronization, etc.
- lightspeed Um programa baseado em OpenGL desenvolvido para ilustrar os efeitos da relatividade especial na aparência de objetos em movimento.
- Animação mostrando as estrelas perto da Terra, vistas de uma espaçonave acelerando rapidamente até a velocidade da luz.

















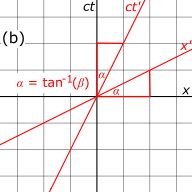

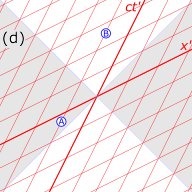









































































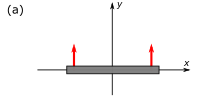



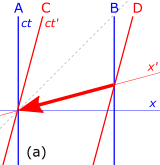














![{\displaystyle \sin \theta '={\frac {\sin \theta }{\gamma [1+(v/c)\cos \theta ]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/04b1d959a5aa9840f249611011e804cba5079e53)























































