Grupo diédrico de ordem 6 - Dihedral group of order 6

Gráfico de Cayley com permutações de um triângulo

Gráfico de ciclo com matrizes de permutações de 3 elementos
(os geradores a e b são iguais aos do gráfico de Cayley mostrado acima.)

Tabela Cayley como tabela de multiplicação das matrizes de permutação

Posições dos seis elementos na tabela de Cayley
Apenas os elementos neutros são simétricos à diagonal principal, portanto, este grupo não é abeliano .

Tabela Cayley como grupo linear geral (e especial ) GL (2, 2)

Em matemática , D ₃ (às vezes alternativamente denotado por D ₆ ) é o grupo diédrico de grau 3, ou, em outras palavras, o grupo diédrico de ordem 6. É isomórfico ao grupo simétrico S ₃ de grau 3. Também é o menor grupo não abeliano possível .

Esta página ilustra muitos conceitos de grupo usando este grupo como exemplo.

Grupos de simetria

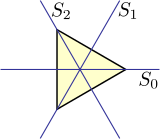
O grupo diédrico D ₃ é o grupo de simetria de um triângulo equilátero , ou seja, é o conjunto de todas as transformações, como reflexão, rotação e combinações destas, que deixam fixa a forma e a posição desse triângulo. No caso de D ₃ , toda permutação possível dos vértices do triângulo constitui tal transformação, de forma que o grupo dessas simetrias é isomorfo ao grupo simétrico S ₃ de todas as permutações de três elementos distintos. Este não é o caso para grupos diédricos de ordens superiores.

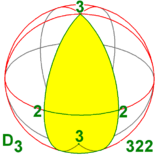
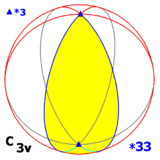
O grupo diédrico D ₃ é isomórfico a dois outros grupos de simetria em três dimensões:

um com um eixo de rotação de 3 vezes e um eixo de rotação de 2 vezes perpendicular (portanto, três destes): D ₃
um com um eixo de rotação de 3 vezes em um plano de reflexão (e, portanto, também em dois outros planos de reflexão): C _3v

Permutações de um conjunto de três objetos

Considere três blocos coloridos (vermelho, verde e azul), inicialmente colocados na ordem RGB. O grupo simétrico S ₃ é então o grupo de todos os rearranjos possíveis desses blocos. Se denotarmos por a a ação "trocar os dois primeiros blocos" e por b a ação "trocar os dois últimos blocos", podemos escrever todas as permutações possíveis em termos dessas duas ações.

Na forma multiplicativa, tradicionalmente escrevemos xy para a ação combinada "primeiro faça y , depois faça x "; de forma que ab é a ação RGB ↦ RBG ↦ BRG , ou seja, "pegue o último bloco e mova-o para frente". Se escrevermos e para "deixar os blocos como estão" (a ação de identidade), podemos escrever as seis permutações do conjunto de três blocos como as seguintes ações:

e : RGB ↦ RGB ou ()
a : RGB ↦ GRB ou (RG)
b : RGB ↦ RBG ou (GB)
ab : RGB ↦ BRG ou (RBG)
ba : RGB ↦ GBR ou (RGB)
aba : RGB ↦ BGR ou (RB)

A notação entre parênteses é a notação do ciclo .

Observe que a ação aa tem o efeito RGB ↦ GRB ↦ RGB , deixando os blocos como estavam; então podemos escrever aa = e . De forma similar,

bb = e ,
( aba ) ( aba ) = e , e
( ab ) ( ba ) = ( ba ) ( ab ) = e ;

portanto, cada uma das ações acima tem um inverso.

Por inspeção, também podemos determinar a associatividade e o fechamento (dois dos axiomas de grupo necessários ); observe por exemplo que

( ab ) a = a ( ba ) = aba , e
( ba ) b = b ( ab ) = bab .

O grupo é não abeliano, pois, por exemplo, ab ≠ ba . Uma vez que é construída a partir de ações básicas a e b , dizemos que o conjunto { a , b } gera -lo.

O grupo tem apresentação

{\ displaystyle \ langle r, a \ mid r ^ {3} = 1, a ^ {2} = 1, ara = r ^ {- 1} \ rangle}

, também escrito

{\ displaystyle \ langle r, a \ mid r ^ {3}, a ^ {2}, arar \ rangle}

ou

{\ displaystyle \ langle a, b \ mid a ^ {2} = b ^ {2} = (ab) ^ {3} = 1 \ rangle}

, também escrito

{\ displaystyle \ langle a, b \ mid a ^ {2}, b ^ {2}, (ab) ^ {3} \ rangle}

onde um e b são permutas e r = AB é uma permutação cíclica. Observe que a segunda apresentação significa que o grupo é um grupo Coxeter . (Na verdade, todos os grupos diédricos e de simetria são grupos Coxeter.)

Resumo das operações do grupo

Com os geradores de um e b , que definem as abreviaturas adicionais c : = aba , d : = AB e F : = ba , de modo que a, b, c, d, e , e f são todos os elementos deste grupo. Podemos então resumir as operações do grupo na forma de uma tabela Cayley :

*	e	uma	b	c	d	f
e	e	uma	b	c	d	f
uma	uma	e	d	f	b	c
b	b	f	e	d	c	uma
c	c	d	f	e	uma	b
d	d	c	uma	b	f	e
f	f	b	c	uma	e	d

Observe que os elementos não iguais e não-identidade comutam apenas se forem inversos uns dos outros. Portanto, o grupo não tem centro , ou seja, o centro do grupo consiste apenas no elemento identidade.

Aulas de conjugação

Podemos facilmente distinguir três tipos de permutações dos três blocos, as classes de conjugação do grupo:

sem mudança (), um elemento de grupo de ordem 1
intercambiando dois blocos: (RG), (RB), (GB), três elementos do grupo de ordem 2
uma permutação cíclica de todos os três blocos: (RGB), (RBG), dois elementos de grupo de ordem 3

Por exemplo, (RG) e (RB) são ambos da forma ( x y ); uma permutação das letras R, G e B (nomeadamente (GB)) muda a notação (RG) para (RB). Portanto, se aplicarmos (GB), então (RB), e então o inverso de (GB), que também é (GB), a permutação resultante é (RG).

Observe que os elementos do grupo conjugado sempre têm a mesma ordem , mas em geral dois elementos do grupo que têm a mesma ordem não precisam ser conjugados.

Subgrupos

A partir do teorema de Lagrange , sabemos que qualquer subgrupo não trivial de um grupo com 6 elementos deve ter ordem 2 ou 3. Na verdade, as duas permutações cíclicas de todos os três blocos, com a identidade, formam um subgrupo de ordem 3, índice 2 e as trocas de dois blocos, cada um com a identidade, formam três subgrupos de ordem 2, índice 3. A existência de subgrupos de ordem 2 e 3 também é uma consequência do teorema de Cauchy .

O primeiro mencionado é {(), (RGB), (RBG)}, o grupo alternado A ₃ .

Os cosets esquerdos e cosets direitos de A ₃ coincidem (como fazem para qualquer subgrupo do índice 2) e consistem em A ₃ e o conjunto de três swaps {(RB), (RG), (BG) }.

Os cosets esquerdos de {(), (RG)} são:

{(), (RG)}
{(RB), (RGB)}
{(GB), (RBG)}

Os cosets certos de {(RG), ()} são:

{(RG), ()}
{(RBG), (RB)}
{(RGB), (GB)}

Assim, A ₃ é normal e os outros três subgrupos não triviais não. O grupo quociente G / A ₃ é isomórfico com C ₂ .

${\ displaystyle G = \ mathrm {A} _ {3} \ rtimes H}$ , um produto semidireto , onde H é um subgrupo de dois elementos: () e um dos três swaps. Esta decomposição também é uma consequência (caso particular) do teorema de Schur – Zassenhaus .

Em termos de permutações, os dois elementos do grupo de G / A ₃ são o conjunto de permutações pares e o conjunto de permutações ímpares.

Se o grupo original é aquele gerado por uma rotação de 120 ° de um plano em torno de um ponto, e reflexão em relação a uma linha através desse ponto, então o grupo de quociente tem os dois elementos que podem ser descritos como os subconjuntos "apenas girar ( ou não fazer nada) "e" tirar uma imagem espelhada ".

Observe que, para o grupo de simetria de um quadrado , uma permutação desigual de vértices não corresponde a obter uma imagem espelhada, mas a operações não permitidas para retângulos , ou seja, rotação de 90 ° e aplicação de um eixo diagonal de reflexão.

Produtos semi-diretos

${\ displaystyle \ mathrm {C} _ {3} \ rtimes _ {\ varphi} \ mathrm {C} _ {2}}$ é se φ (0) e φ (1) são a identidade. O produto semidireto é isomórfico ao grupo diédrico de ordem 6 se φ (0) é a identidade e φ (1) é o automorfismo não trivial de C ₃ , que inverte os elementos. ${\ displaystyle \ mathrm {C} _ {3} \ times \ mathrm {C} _ {2}}$

Assim, obtemos:

( n ₁ , 0) * ( n ₂ , h ₂ ) = ( n ₁ + n ₂ , h ₂ )

( n ₁ , 1) * ( n ₂ , h ₂ ) = ( n ₁ - n ₂ , 1 + h ₂ )

para todo n ₁ , n ₂ em C ₃ e h ₂ em C ₂ . Mais concisamente,

{\ displaystyle (n_ {1}, h_ {1}) * (n_ {2}, h_ {2}) = (n_ {1} + (- 1) ^ {h_ {1}} n_ {2}, h_ {1} + h_ {2})}

para todo n ₁ , n ₂ em C ₃ e h ₁ , h ₂ em C ₂ .

Em uma mesa Cayley:

	00	10	20	01	11	21
00	00	10	20	01	11	21
10	10	20	00	11	21	01
20	20	00	10	21	01	11
01	01	21	11	00	20	10
11	11	01	21	10	00	20
21	21	11	01	20	10	00

Observe que, para o segundo dígito, temos essencialmente uma tabela 2 × 2, com 3 × 3 valores iguais para cada uma dessas 4 células. Para o primeiro dígito, a metade esquerda da tabela é igual à metade direita, mas a metade superior é diferente da metade inferior.

Para o produto direto, a tabela é a mesma, exceto que os primeiros dígitos da metade inferior da tabela são os mesmos da metade superior.

Ação em grupo

Considere D ₃ na forma geométrica, como um grupo de simetria de isometrias do plano, e considere a ação do grupo correspondente em um conjunto de 30 pontos uniformemente espaçados em um círculo, numerados de 0 a 29, com 0 em um dos eixos de reflexão.

Esta seção ilustra os conceitos de ação de grupo para este caso.

A ação de G em X é chamada

transitivo se para quaisquer dois x , y em X existe um g em G tal que g · x = y ; Este não é o caso
fiel (ou eficaz ) se para quaisquer dois diferentes g , h em G existe um x em X tal que g · x ≠ h · x ; este é o caso, porque, exceto para a identidade, os grupos de simetria não contêm elementos que "não fazem nada"
livre se para quaisquer dois g diferentes , h em G e todo x em X temos g · x ≠ h · x ; este não é o caso porque há reflexos

Órbitas e estabilizadores

As órbitas de 30 pontos uniformemente espaçados em um círculo sob a ação de grupo de D3

A órbita de um ponto X em X é o conjunto de elementos de X para que x pode ser movidas por os elementos de L . A órbita de x é denotada por Gx :

{\ displaystyle Gx = \ left \ {g \ cdot x \ mid g \ in G \ right \}}

As órbitas são {0, 10, 20}, {1, 9, 11, 19, 21, 29}, {2, 8, 12, 18, 22, 28}, {3, 7, 13, 17, 23, 27}, {4, 6, 14, 16, 24, 26} e {5, 15, 25}. Os pontos dentro de uma órbita são "equivalentes". Se um grupo de simetria se aplica a um padrão, então, dentro de cada órbita, a cor é a mesma.

O conjunto de todas as órbitas de X sob a acção de L está escrito como X / L .

Se Y é um subconjunto de X , escrevemos GY para o conjunto { g · y : y ∈ Y e g ∈ G }. Chamamos o subconjunto Y de invariante em G se GY = Y (que é equivalente a GY ⊆ Y ) . Nesse caso, L também opera em Y . O subconjunto Y é chamado fixo em G se g · y = y para todas g em L e todos Y em Y . A união de, por exemplo, duas órbitas é invariante em G , mas não fixa.

Para cada x em X , definimos o subgrupo estabilizador de x (também chamado de grupo de isotropia ou pequeno grupo ) como o conjunto de todos os elementos em G que fixam x :

{\ displaystyle G_ {x} = \ {g \ in G \ mid g \ cdot x = x \}}

Se x é um ponto de reflexão (0, 5, 10, 15, 20 ou 25) , seu estabilizador é o grupo de ordem dois contendo a identidade e o reflexo em x . Em outros casos, o estabilizador é o grupo trivial.

Para um x fixo em X , considere o mapa de G a X dado por g ↦ g · x . A imagem deste mapa é a órbita de x eo coimagem é o conjunto de todas as esquerdas cosets de G _x . O teorema do quociente padrão da teoria dos conjuntos fornece então uma bijeção natural entre G / G _x e Gx . Especificamente, a bijeção é dada por hG _x ↦ h · x . Este resultado é conhecido como teorema do estabilizador de órbita . Nos dois casos de órbita pequena, o estabilizador não é trivial.

Se dois elementos de x e y pertencem à mesma órbita, em seguida, os seus subgrupos estabilizador, L _x e G _y , são isomorfos . Mais precisamente: se y = g · x , então G _y = gG _x g ⁻¹ . No exemplo, isso se aplica, por exemplo, para 5 e 25, ambos os pontos de reflexão. A reflexão de cerca de 25 corresponde a uma rotação de 10, a reflexão de cerca de 5 e a rotação de -10.

Um resultado intimamente relacionado ao teorema do estabilizador de órbita é o lema de Burnside :

{\ displaystyle \ left | X / G \ right | = {\ frac {1} {\ left | G \ right |}} \ sum _ {g \ in G} \ left | X ^ {g} \ right |}

onde X ^g é o conjunto de pontos fixados por g . Ou seja, o número de órbitas é igual ao número médio de pontos fixados por elemento do grupo.

Para a identidade todos os 30 pontos são fixos, para as duas rotações nenhum e para as três reflexões dois cada: {0, 15}, {5, 20} e {10, 25}. Assim, a média é seis, o número de órbitas.

Teoria da representação

Até o isomorfismo, este grupo possui três representações unitárias complexas irredutíveis, que chamaremos de (a representação trivial), e , onde o subscrito indica a dimensão. Por sua definição como um grupo de permutação sobre o conjunto de três elementos, o grupo tem uma representação por permutando as entradas do vetor, a representação fundamental. Essa representação não é irredutível, pois se decompõe como uma soma direta de e . aparece como o subespaço de vetores da forma e é a representação em seu complemento ortogonal, que são vetores da forma . A representação unidimensional não trivial surge por meio da graduação dos grupos : A ação é a multiplicação pelo sinal da permutação do elemento do grupo. Todo grupo finito tem tal representação, uma vez que é um subgrupo de um grupo cíclico por sua ação regular. Contando as dimensões quadradas das representações ( , a ordem do grupo), vemos que essas devem ser todas as representações irredutíveis. ${\ displaystyle I}$ ${\ displaystyle \ rho _ {1}}$ ${\ displaystyle \ rho _ {2}}$ ${\ displaystyle \ mathbb {C} ^ {3}}$ ${\ displaystyle I}$ ${\ displaystyle \ rho _ {2}}$ ${\ displaystyle I}$ ${\ displaystyle (\ lambda, \ lambda, \ lambda), \ lambda \ in \ mathbb {C}}$ ${\ displaystyle \ rho _ {2}}$ ${\ displaystyle (\ lambda _ {1}, \ lambda _ {2}, - \ lambda _ {1} - \ lambda _ {2})}$ ${\ displaystyle \ rho _ {1}}$ ${\ displaystyle \ mathbb {Z} _ {2}}$ ${\ displaystyle 1 ^ {2} + 1 ^ {2} + 2 ^ {2} = 6}$

Uma representação linear irredutível bidimensional produz uma representação projetiva unidimensional (isto é, uma ação na linha projetiva , uma incorporação no grupo Möbius PGL (2, C ) ), como transformadas elípticas . Isso pode ser representado por matrizes com entradas 0 e ± 1 (aqui escritas como transformações lineares fracionárias ), conhecido como grupo anarmônico :

pedido 1: ${\ displaystyle z}$
pedido 2: ${\ displaystyle 1-z, 1 / z, z / (z-1)}$
pedido 3: ${\ displaystyle (z-1) / z, 1 / (1-z)}$

e, assim, desce a uma representação sobre qualquer campo, que é sempre fiel / injetiva (uma vez que dois termos não diferem apenas por um sinal). Sobre o campo com dois elementos, a linha projetiva tem apenas 3 pontos, e este é, portanto, o isomorfismo excepcional. Na característica 3, esse embedding estabiliza o ponto, uma vez que (na característica maior que 3 esses pontos são distintos e permutados, e são a órbita de a razão cruzada harmônica ). Sobre o campo com três elementos, a linha projetiva tem 4 elementos, e como PGL (2, 3) é isomórfico ao grupo simétrico em 4 elementos, S ₄ , o embutimento resultante é igual ao estabilizador do ponto . ${\ displaystyle S_ {3} \ approx \ mathrm {PGL} (2,2).}$ ${\ displaystyle -1 = [- 1: 1],}$ ${\ displaystyle 2 = 1/2 = -1}$ ${\ displaystyle \ mathrm {S} _ {3} \ hookrightarrow \ mathrm {S} _ {4}}$ ${\ displaystyle -1}$