Grupo diédrico - Dihedral group

O grupo de simetria de um floco de neve é D ₆ , uma simetria diedral, a mesma de um hexágono regular .

Em matemática , um grupo diedro é o grupo de simetrias de um polígono regular , que inclui rotações e reflexos . Os grupos diédricos estão entre os exemplos mais simples de grupos finitos e desempenham um papel importante na teoria dos grupos , geometria e química .

A notação para o grupo diédrico difere em geometria e álgebra abstrata . Em geometria , $D n$ ou $Dih n$ refere-se às simetrias do $n$ -gon , um grupo de ordem $2 n$ . Na álgebra abstrata , $D 2 n$ refere-se a este mesmo grupo diedro. A convenção geométrica é usada neste artigo.

Definição

Elementos

Os seis eixos de reflexão de um hexágono regular

Um polígono regular com lados tem diferentes simetrias: simetrias rotacionais e simetrias de reflexão . Normalmente, levamos aqui. As rotações e reflexões associadas constituem o grupo diedro . Se for ímpar, cada eixo de simetria conecta o ponto médio de um lado ao vértice oposto. Se for par, existem eixos de simetria conectando os pontos médios de lados opostos e eixos de simetria conectando vértices opostos. Em ambos os casos, existem eixos de simetria e elementos no grupo de simetria. Refletir em um eixo de simetria seguido de refletir em outro eixo de simetria produz uma rotação por meio do dobro do ângulo entre os eixos. ${\ displaystyle n}$ ${\ displaystyle 2n}$ ${\ displaystyle n}$ ${\ displaystyle n}$ ${\ displaystyle n \ geq 3}$ ${\ displaystyle \ mathrm {D} _ {n}}$ ${\ displaystyle n}$ ${\ displaystyle n}$ ${\ displaystyle n / 2}$ ${\ displaystyle n / 2}$ ${\ displaystyle n}$ ${\ displaystyle 2n}$

A imagem a seguir mostra o efeito dos dezesseis elementos de em um sinal de parada : ${\ displaystyle \ mathrm {D} _ {8}}$

A primeira linha mostra o efeito das oito rotações, e a segunda linha mostra o efeito das oito reflexões, em cada caso atuando no sinal de parada com a orientação mostrada no canto superior esquerdo.

Estrutura de grupo

Como acontece com qualquer objeto geométrico, a composição de duas simetrias de um polígono regular é novamente uma simetria desse objeto. Com a composição de simetrias para produzir outra como a operação binária, isso dá às simetrias de um polígono a estrutura algébrica de um grupo finito .

As linhas de reflexão marcadas S ₀ , S ₁ e S ₂ permanecem fixas no espaço (na página) e não se movem quando uma operação de simetria (rotação ou reflexão) é feita no triângulo (isso é importante ao fazer composições de simetrias )

A composição dessas duas reflexões é uma rotação.

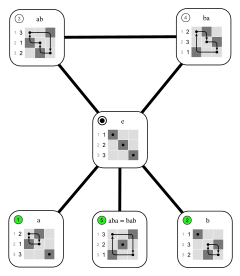
A seguinte tabela de Cayley mostra o efeito da composição no grupo D ₃ (as simetrias de um triângulo equilátero ). r ₀ denota a identidade; r ₁ e r ₂ denotam rotações no sentido anti-horário em 120 ° e 240 °, respectivamente, e s ₀ , s ₁ e s ₂ denotam reflexos através das três linhas mostradas na imagem adjacente.

	r ₀	r ₁	r ₂	s ₀	s ₁	s ₂
r ₀	r ₀	r ₁	r ₂	s ₀	s ₁	s ₂
r ₁	r ₁	r ₂	r ₀	s ₁	s ₂	s ₀
r ₂	r ₂	r ₀	r ₁	s ₂	s ₀	s ₁
s ₀	s ₀	s ₂	s ₁	r ₀	r ₂	r ₁
s ₁	s ₁	s ₀	s ₂	r ₁	r ₀	r ₂
s ₂	s ₂	s ₁	s ₀	r ₂	r ₁	r ₀

Por exemplo, s ₂ s ₁ = r ₁ , porque a reflexão s ₁ seguida pela reflexão s ₂ resulta em uma rotação de 120 °. A ordem dos elementos que denotam a composição é da direita para a esquerda, refletindo a convenção de que o elemento atua na expressão à sua direita. A operação de composição não é comutativa .

Em geral, o grupo D _n possui elementos r ₀ , ..., r _{n −1} e s ₀ , ..., s _{n −1} , com composição dada pelas seguintes fórmulas:

{\ displaystyle \ mathrm {r} _ {i} \, \ mathrm {r} _ {j} = \ mathrm {r} _ {i + j}, \ quad \ mathrm {r} _ {i} \, \ mathrm {s} _ {j} = \ mathrm {s} _ {i + j}, \ quad \ mathrm {s} _ {i} \, \ mathrm {r} _ {j} = \ mathrm {s} _ {ij}, \ quad \ mathrm {s} _ {i} \, \ mathrm {s} _ {j} = \ mathrm {r} _ {ij}.}

Em todos os casos, a adição e subtração de subscritos devem ser realizadas usando aritmética modular com módulo n .

Representação matricial

As simetrias desse pentágono são transformações lineares do plano como um espaço vetorial.

Se centrarmos o polígono regular na origem, os elementos do grupo diédrico atuam como transformações lineares do plano . Isso nos permite representar os elementos de D _n como matrizes , com a composição sendo a multiplicação da matriz . Este é um exemplo de representação de grupo (bidimensional) .

Por exemplo, os elementos do grupo D ₄ podem ser representados pelas seguintes oito matrizes:

{\ displaystyle {\ begin {matrix} \ mathrm {r} _ {0} = \ left ({\ begin {smallmatrix} 1 & 0 \\ [0.2em] 0 & 1 \ end {smallmatrix}} \ right), & \ mathrm { r} _ {1} = \ left ({\ begin {smallmatrix} 0 & -1 \\ [0.2em] 1 & 0 \ end {smallmatrix}} \ right), & \ mathrm {r} _ {2} = \ left ( {\ begin {smallmatrix} -1 & 0 \\ [0.2em] 0 & -1 \ end {smallmatrix}} \ right), & \ mathrm {r} _ {3} = \ left ({\ begin {smallmatrix} 0 & 1 \\ [0.2em] -1 & 0 \ end {smallmatrix}} \ right), \\ [1em] \ mathrm {s} _ {0} = \ left ({\ begin {smallmatrix} 1 & 0 \\ [0.2em] 0 & -1 \ end {smallmatrix}} \ right), & \ mathrm {s} _ {1} = \ left ({\ begin {smallmatrix} 0 & 1 \\ [0.2em] 1 & 0 \ end {smallmatrix}} \ right), & \ mathrm {s} _ {2} = \ left ({\ begin {smallmatrix} -1 & 0 \\ [0.2em] 0 & 1 \ end {smallmatrix}} \ right), & \ mathrm {s} _ {3} = \ left ({\ begin {smallmatrix} 0 & -1 \\ [0.2em] -1 & 0 \ end {smallmatrix}} \ right). \ end {matrix}}}

Em geral, as matrizes para elementos de D _n têm a seguinte forma:

{\ displaystyle {\ begin {alinhados} \ mathrm {r} _ {k} & = {\ begin {pmatrix} \ cos {\ frac {2 \ pi k} {n}} & - \ sin {\ frac {2 \ pi k} {n}} \\\ sin {\ frac {2 \ pi k} {n}} & \ cos {\ frac {2 \ pi k} {n}} \ end {pmatrix}} \ \ { \ text {and}} \\\ mathrm {s} _ {k} & = {\ begin {pmatrix} \ cos {\ frac {2 \ pi k} {n}} & \ sin {\ frac {2 \ pi k} {n}} \\\ sin {\ frac {2 \ pi k} {n}} & - \ cos {\ frac {2 \ pi k} {n}} \ end {pmatrix}}. \ end { alinhado}}}

r _k é uma matriz de rotação , expressando uma rotação no sentido anti-horário através de um ângulo de 2 πk / n . s _k é um reflexo através de uma linha que forma um ângulo de πk / n com o eixo x .

Outras definições

Outras definições equivalentes de $D n$ são:

O grupo de automorfismo do gráfico consiste apenas em um ciclo com n vértices (se n ≥ 3).
O grupo com apresentação
${\ displaystyle {\ begin {alinhado} \ mathrm {D} _ {n} & = \ left \ langle \ mathrm {r}, \ mathrm {s} \ mid \ operatorname {ord} (\ mathrm {r}) = n, \ operatorname {ord} (\ mathrm {s}) = 2, \ mathrm {srs} = \ mathrm {r} ^ {- 1} \ right \ rangle \\ & = \ left \ langle \ mathrm {r, s} \ mid \ mathrm {r} ^ {n} = \ mathrm {s} ^ {2} = (\ mathrm {sr}) ^ {2} = 1 \ direita \ rangle. \ end {alinhado}}}$
Da segunda apresentação segue que $D n$ pertence à classe dos grupos de Coxeter .
O produto semidireto dos grupos cíclicos $Z n$ e $Z 2$ , com $Z 2$ agindo em $Z n$ por inversão (assim, $D n$ sempre tem um subgrupo normal isomórfico ao grupo $Z n$ ). Z _n ⋊ _φ Z ₂ é isomorfo a $D n$ se $φ (0)$ for a identidade e $φ (1)$ for inversão.

Pequenos grupos diédricos

Exemplos de subgrupos de uma simetria diédrica hexagonal

$D 1$ é isomórfico a $Z 2$ , o grupo cíclico de ordem 2.

$D 2$ é isomórfico a $K 4$ , o quatro grupo de Klein .

$D 1$ e $D 2$ são excepcionais em que:

$D 1$ e $D 2$ são os únicos grupos diédricos abelianos . Caso contrário, $D n$ é não abeliano.
$D n$ é um subgrupo do grupo simétrico $S n$ para $n \geq 3$ . Como $2 n > n!$ para $n = 1$ ou $n = 2$ , para esses valores, $D n$ é muito grande para ser um subgrupo.
O grupo de automorfismo interno de $D 2$ é trivial, enquanto para outros valores pares de $n$ , é $D n / Z 2$ .

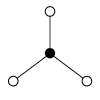
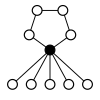
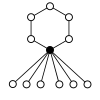
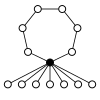
Os gráficos de ciclo de grupos diédricos consistem em um ciclo de n elementos e n ciclos de 2 elementos. O vértice escuro nos gráficos de ciclo abaixo de vários grupos diédricos representa o elemento de identidade, e os outros vértices são os outros elementos do grupo. Um ciclo consiste em poderes sucessivos de qualquer um dos elementos conectados ao elemento de identidade .

Gráficos de ciclo
D ₁ = Z ₂	D ₂ = Z ₂² = K ₄	D ₃	D ₄	D ₅


D ₆ = D ₃ × Z ₂	D ₇	D ₈	D ₉	D ₁₀ = D ₅ × Z ₂

D ₃ = S ₃	D ₄

O grupo diédrico como grupo de simetria em 2D e grupo de rotação em 3D

Um exemplo de grupo abstrato $D n$ , e uma forma comum de visualizá-lo, é o grupo de isometrias do plano euclidiano que mantém a origem fixa. Esses grupos formam uma das duas séries de grupos de pontos discretos em duas dimensões . $D n$ consiste em $n$ rotações de múltiplos de $360 ° / n$ sobre a origem e reflexos através de $n$ linhas através da origem, criando ângulos de múltiplos de $180 ° / n$ entre si. Este é o grupo de simetria de um polígono regular com $n$ lados (para $n \geq 3$ ; isso se estende aos casos $n = 1$ e $n = 2$ onde temos um plano com, respectivamente, um ponto deslocado do "centro" do "1- gon "e um" 2-gon "ou segmento de linha).

$D n$ é gerado por uma rotação $r$ de ordem $n$ e uma reflexão $s$ de ordem 2, de modo que

{\ displaystyle \ mathrm {srs} = \ mathrm {r} ^ {- 1} \,}

Em termos geométricos: no espelho, uma rotação parece uma rotação inversa.

Em termos de números complexos : multiplicação por e conjugação complexa . ${\ displaystyle e ^ {2 \ pi i \ over n}}$

Em forma de matriz, definindo

{\ displaystyle \ mathrm {r} _ {1} = {\ begin {bmatrix} \ cos {2 \ pi \ over n} & - \ sin {2 \ pi \ over n} \\ [4pt] \ sin {2 \ pi \ over n} & \ cos {2 \ pi \ over n} \ end {bmatrix}} \ qquad \ mathrm {s} _ {0} = {\ begin {bmatrix} 1 & 0 \\ 0 & -1 \ end { bmatrix}}}

e definir e para nós podemos escrever as regras do produto para D _n como ${\ displaystyle \ mathrm {r} _ {j} = \ mathrm {r} _ {1} ^ {j}}$ ${\ displaystyle \ mathrm {s} _ {j} = \ mathrm {r} _ {j} \, \ mathrm {s} _ {0}}$ ${\ displaystyle j \ in \ {1, \ ldots, n-1 \}}$

{\ displaystyle {\ begin {alinhado} \ mathrm {r} _ {j} \, \ mathrm {r} _ {k} & = \ mathrm {r} _ {(j + k) {\ text {mod}} n} \\\ mathrm {r} _ {j} \, \ mathrm {s} _ {k} & = \ mathrm {s} _ {(j + k) {\ text {mod}} n} \\\ mathrm {s} _ {j} \, \ mathrm {r} _ {k} & = \ mathrm {s} _ {(jk) {\ text {mod}} n} \\\ mathrm {s} _ {j } \, \ mathrm {s} _ {k} & = \ mathrm {r} _ {(jk) {\ text {mod}} n} \ end {alinhado}}}

(Compare rotações e reflexos de coordenadas .)

O grupo diédrico D ₂ é gerado pela rotação r de 180 graus e a reflexão s através do eixo x . Os elementos de D ₂ podem então ser representados como {e, r, s, rs}, onde e é a identidade ou transformação nula e rs é o reflexo através do eixo y .

Os quatro elementos de D ₂ (o eixo x é vertical aqui)

D ₂ é isomórfico ao quatro grupo de Klein .

Para n > 2 as operações de rotação e reflexão em geral não comutam e D _n não é abeliano ; por exemplo, em D ₄ , uma rotação de 90 graus seguida por uma reflexão produz um resultado diferente de uma reflexão seguida por uma rotação de 90 graus.

D ₄ é nonabelian (o eixo x é vertical aqui).

Assim, além de sua aplicação óbvia a problemas de simetria no plano, esses grupos estão entre os exemplos mais simples de grupos não abelianos, e como tais surgem freqüentemente como contraexemplos fáceis para teoremas que são restritos a grupos abelianos.

Os $2 n$ elementos de $D n$ podem ser escritos como $e$ , $r$ , $r 2$ , ..., $r n -1$ , $s$ , $rs$ , $r 2 s$ , ..., $r n -1 s$ . Os primeiros $n$ elementos listados são rotações e os $n$ elementos restantes são reflexos de eixo (todos os quais têm ordem 2). O produto de duas rotações ou duas reflexões é uma rotação; o produto de uma rotação e um reflexo é um reflexo.

Até agora, consideramos $D n$ como um subgrupo de $O (2)$ , ou seja, o grupo de rotações (sobre a origem) e reflexões (através dos eixos através da origem) do plano. No entanto, a notação $D n$ também é usada para um subgrupo de SO (3) que também é do tipo de grupo abstrato $D n$ : o grupo de simetria adequado de um polígono regular embutido no espaço tridimensional (se n ≥ 3). Tal figura pode ser considerada como um sólido regular degenerado com sua face contada duas vezes. Portanto, também é chamado de diedro (grego: sólido com duas faces), o que explica o nome grupo diédrico (em analogia ao grupo tetraédrico , octaédrico e icosaédrico , referindo-se aos grupos de simetria próprios de um tetraedro regular , octaedro e icosaedro, respectivamente )

Exemplos de simetria diedral 2D

Simetria 2D D ₆ - A Estrela de Davi Vermelha
Simetria 2D D ₁₆ - Selo Imperial do Japão, representando crisântemo óctuplo com dezesseis pétalas .
Simetria 2D D ₂₄ - Ashoka Chakra , conforme representado na bandeira nacional da República da Índia .

Propriedades

As propriedades dos grupos diédricos $D n$ com $n \geq 3$ dependem se $n$ é par ou ímpar. Por exemplo, o centro de $D n$ consiste apenas na identidade se n for ímpar, mas se n for par, o centro tem dois elementos, nomeadamente a identidade e o elemento r ^{n / 2} (com D _n como um subgrupo de O (2 ), isso é inversão ; uma vez que é multiplicação escalar por −1, é claro que comuta com qualquer transformação linear).

No caso de isometrias 2D, isso corresponde a adicionar inversão, dando rotações e espelhos entre os existentes.

Para n duas vezes um número ímpar, o grupo abstrato $D n$ é isomórfico com o produto direto de $D n / 2$ e $Z 2$ . Geralmente, se m divide n , então $D n$ tem subgrupos n / m do tipo $D$ $m$ , e um subgrupo ℤ _m . Portanto, o número total de subgrupos de $D$ $n$ ( n ≥ 1), é igual a d ( n ) + σ ( n ), onde d ( n ) é o número de divisores positivos de n e σ ( n ) é a soma dos divisores positivos de n . Veja a lista de pequenos grupos para os casos n ≤ 8.

O grupo didrico de ordem 8 (D ₄ ) é o menor exemplo de um grupo que não é um t-grupo . Qualquer um dos seus dois subgrupos de quatro grupos de Klein (que são normais em D ₄ ) tem como subgrupos normais a ordem de 2 subgrupos gerados por uma reflexão (flip) em D ₄ , mas esses subgrupos não são normais em D ₄ .

Aulas de conjugação de reflexões

Todas as reflexões são conjugadas entre si caso n seja ímpar, mas elas se enquadram em duas classes de conjugação se n for par. Se pensarmos nas isometrias de um n- gon regular : para n ímpar, há rotações no grupo entre cada par de espelhos, enquanto para n par apenas metade dos espelhos pode ser alcançada de um por meio dessas rotações. Geometricamente, em um polígono ímpar todo eixo de simetria passa por um vértice e um lado, enquanto em um polígono par existem dois conjuntos de eixos, cada um correspondendo a uma classe de conjugação: aqueles que passam por dois vértices e aqueles que passam por dois lados .

Algebricamente, esta é uma instância do teorema de Sylow conjugado (para n ímpar): para n ímpar, cada reflexão, juntamente com a identidade, forma um subgrupo de ordem 2, que é um subgrupo de Sylow 2 ( 2 = 2 ¹ é o potência máxima de 2 dividindo 2 n = 2 [2 k + 1] ), enquanto para n par, esses subgrupos de ordem 2 não são subgrupos de Sylow porque 4 (uma potência maior de 2) divide a ordem do grupo.

Pois n mesmo existe, em vez disso, um automorfismo externo trocando os dois tipos de reflexos (propriamente, uma classe de automorfismo externo, que são todos conjugados por um automorfismo interno).

Grupo de automorfismo

O grupo de automorfismo de $D n$ é isomorfo ao holomorfo de ℤ / n ℤ, ou seja, a Hol (ℤ / n ℤ) = { ax + b | ( a , n ) = 1} e tem ordem nϕ ( n ), onde ϕ é a função totiente de Euler , o número de k em 1,…, n - 1 coprime para n .

Pode ser entendido em termos dos geradores de uma reflexão e uma rotação elementar (rotação por k (2 π / n ), para k coprime para n ); quais automorfismos são internos e externos depende da paridade de n .

Para n ímpar, o grupo diédrico não tem centro, portanto, qualquer elemento define um automorfismo interno não trivial; para n par, a rotação de 180 ° (reflexão através da origem) é o elemento não trivial do centro.
Assim, para n ímpar, o grupo de automorfismo interno tem ordem 2 n , e para n par (diferente de n = 2 ) o grupo de automorfismo interno tem ordem n .
Para n ímpar, todas as reflexões são conjugadas; para n even, eles caem em duas classes (aqueles através de dois vértices e aqueles através de duas faces), relacionadas por um automorfismo externo, que pode ser representado por rotação por π / n (metade da rotação mínima).
As rotações são um subgrupo normal; a conjugação por um reflexo muda o sinal (direção) da rotação, mas de outra forma os deixa inalterados. Assim que automorphisms ângulos de multiplicar por K (coprimas a N ) são exterior, a menos que k = ± 1 .

Exemplos de grupos de automorfismo

$D 9$ tem 18 automorfismos internos . Como grupo de isometria 2D D ₉ , o grupo possui espelhos em intervalos de 20 °. Os 18 automorfismos internos fornecem rotação dos espelhos em múltiplos de 20 ° e reflexos. Como grupo de isometria, todos são automorfismos. Como grupo abstrato existem, além destes, 36 automorfismos externos ; por exemplo, multiplicando os ângulos de rotação por 2.

$D 10$ tem 10 automorfismos internos. Como grupo de isometria 2D D ₁₀ , o grupo possui espelhos em intervalos de 18 °. Os 10 automorfismos internos fornecem rotação dos espelhos em múltiplos de 36 ° e reflexos. Como grupo de isometria, existem mais 10 automorfismos; são conjugados por isometrias fora do grupo, girando os espelhos 18 ° com respeito aos automorfismos internos. Como grupo abstrato, existem além desses 10 automorfismos internos e 10 externos, mais 20 automorfismos externos; por exemplo, multiplicar as rotações por 3.

Compare os valores 6 e 4 para a função totiente de Euler , o grupo multiplicativo de inteiros módulo n para n = 9 e 10, respectivamente. Isso triplica e dobra o número de automorfismos em comparação com os dois automorfismos como isometrias (mantendo a mesma ordem das rotações ou invertendo a ordem).

Os únicos valores de n para os quais φ ( n ) = 2 são 3, 4 e 6 e, consequentemente, existem apenas três grupos diédricos que são isomórficos aos seus próprios grupos de automorfismo, a saber $D 3$ (ordem 6), $D 4$ ( pedido 8) e $D 6$ (pedido 12).

Grupo de automorfismo interno

O grupo de automorfismo interno de $D n$ é isomórfico a:

$D n$ se n for ímpar;
$D n / Z 2$ se $n$ for par (para $n = 2$ , $D 2 / Z 2 = 1$ ).

Generalizações

Existem várias generalizações importantes dos grupos diédricos:

O grupo diédrico infinito é um grupo infinito com estrutura algébrica semelhante aos grupos diédricos finitos. Ele pode ser visto como o grupo de simetrias dos inteiros .
O grupo ortogonal O (2), ou seja, o grupo de simetria do círculo , também possui propriedades semelhantes aos grupos diédricos.
A família de grupos diédricos generalizados inclui ambos os exemplos acima, bem como muitos outros grupos.
Os grupos quase-diédricos são famílias de grupos finitos com propriedades semelhantes aos grupos diédricos.

Veja também

Referências

links externos

Grupo diédrico n de Ordem 2n por Shawn Dudzik, Projeto de Demonstrações do Wolfram .
Grupo diédrico em Groupprops
Weisstein, Eric W. "Dihedral Group" . MathWorld .
Weisstein, Eric W. "Dihedral Group D3" . MathWorld .
Weisstein, Eric W. "Dihedral Group D4" . MathWorld .
Weisstein, Eric W. "Dihedral Group D5" . MathWorld .
Davis, Declan. "Grupo Diédrico D6" . MathWorld .
Grupos diédricos em GroupNames

Languages

In other projects