Grupo alternado - Alternating group
|
Estrutura algébrica → Teoria de grupos Teoria de grupos |
|---|
 |
Em matemática , um grupo alternado é o grupo de permutações pares de um conjunto finito . O grupo alternado em um conjunto de n elementos é chamado de grupo alternado de grau n , ou o grupo alternado de n letras e denotado por A n ou Alt ( n ).
Propriedades básicas
Para n > 1 , o grupo A n é o subgrupo comutador do grupo simétrico S n com índice 2 e, portanto, n ! / 2 elementos. É o núcleo do homomorfismo do grupo de assinatura sgn: S n → {1, −1} explicado em grupo simétrico .
O grupo A n é abeliano se e somente se n ≤ 3 e simples se e somente se n = 3 ou n ≥ 5 . A 5 é o menor grupo simples não abeliano , tendo ordem 60, e o menor grupo não solucionável .
O grupo A 4 tem o grupo V de Klein quatro como um subgrupo normal próprio , ou seja, a identidade e as transposições duplas {(), (12) (34), (13) (24), (14) (23)} , esse é o cerne da sobreposição de A 4 em A 3 = Z 3 . Temos a sequência exata V → A 4 → A 3 = Z 3 . Na teoria de Galois , este mapa, ou melhor, o mapa correspondente S 4 → S 3 , corresponde a associar o resolvente de Lagrange cúbico a um quártico, o que permite que o polinômio quártico seja resolvido por radicais, conforme estabelecido por Lodovico Ferrari .
Aulas de conjugação
Como no grupo simétrico , quaisquer dois elementos de A n que são conjugados por um elemento de A n devem ter a mesma forma de ciclo . O inverso não é necessariamente verdadeiro, no entanto. Se a forma do ciclo consiste apenas em ciclos de comprimento ímpar, sem dois ciclos do mesmo comprimento, onde os ciclos de comprimento um são incluídos no tipo de ciclo, então existem exatamente duas classes de conjugação para esta forma de ciclo ( Scott 1987 , §11.1, p299 )
Exemplos:
- As duas permutações (123) e (132) não são conjugadas em A 3 , embora tenham a mesma forma de ciclo e, portanto, são conjugadas em S 3 .
- A permutação (123) (45678) não é conjugada com seu inverso (132) (48765) em A 8 , embora as duas permutações tenham a mesma forma de ciclo, portanto, são conjugadas em S 8 .
Relação com grupo simétrico
- Veja grupo simétrico .
Geradores e relações
Um n é gerado por 3 ciclos, uma vez que 3 ciclos podem ser obtidos combinando pares de transposições. Este conjunto gerador é freqüentemente usado para provar que A n é simples para n ≥ 5 .
Grupo de automorfismo
| n | Aut (A n ) | Fora (A n ) |
|---|---|---|
| n ≥ 4, n ≠ 6 | S n | Z 2 |
| n = 1, 2 | Z 1 | Z 1 |
| n = 3 | Z 2 | Z 2 |
| n = 6 | S 6 ⋊ Z 2 | V = Z 2 × Z 2 |
Para n > 3 , exceto para n = 6 , o grupo de automorfismo de A n é o grupo simétrico S n , com grupo de automorfismo interno A n e grupo de automorfismo externo Z 2 ; o automorfismo externo vem da conjugação por uma permutação ímpar.
Para n = 1 e 2, o grupo de automorfismo é trivial. Para n = 3, o grupo de automorfismo é Z 2 , com grupo de automorfismo interno trivial e grupo de automorfismo externo Z 2 .
O grupo de automorfismo externo de A 6 é o quatro grupos de Klein V = Z 2 × Z 2 e está relacionado ao automorfismo externo de S 6 . O automorfismo externo extra em A 6 troca os 3 ciclos (como (123)) com elementos de forma 3 2 (como (123) (456) ).
Isomorfismos excepcionais
Existem alguns isomorfismos excepcionais entre alguns dos pequenos grupos alternados e pequenos grupos do tipo Lie , particularmente grupos lineares especiais projetivos . Estes são:
- A 4 é isomórfico ao PSL 2 (3) e ao grupo de simetria da simetria tetraédrica quiral .
- A 5 é isomórfico a PSL 2 (4), PSL 2 (5) e ao grupo de simetria de simetria icosaédrica quiral . (Veja para um isomorfismo indireto de PSL 2 (F 5 ) → A 5 usando uma classificação de grupos simples de ordem 60, e aqui para uma prova direta).
- A 6 é isomórfico a PSL 2 (9) e PSp 4 (2) '.
- A 8 é isomórfico ao PSL 4 (2).
Mais obviamente, A 3 é isomórfico ao grupo cíclico Z 3 e A 0 , A 1 e A 2 são isomórficos ao grupo trivial (que também é SL 1 ( q ) = PSL 1 ( q ) para qualquer q ).
Exemplos S 4 e A 4

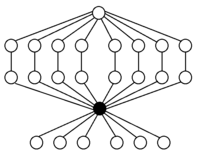
Tabela Cayley do grupo simétrico S 4
As permutações ímpares são coloridas: Transposições em verde e 4 ciclos em laranja |

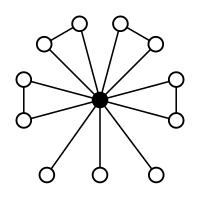
Tabela de Cayley do grupo alternado A 4
Elementos: As permutações pares (a identidade, oito 3 ciclos e três transposições duplas (transposições duplas em negrito)) Subgrupos:     
|
 A 3 = Z 3 (pedido 3) |
 A 4 (pedido 12) |
 A 4 × Z 2 (pedido 24) |
 S 3 = Dih 3 (pedido 6) |
 S 4 (pedido 24) |
 A 4 em S 4 à esquerda |
Exemplo A 5 como um subgrupo de rotações de 3 espaços
A 5 é o grupo de isometrias de um dodecaedro no espaço 3, então há uma representação A 5 → SO 3 ( R ) .
Nesta figura, os vértices dos poliedros representam os elementos do grupo, com o centro da esfera representando o elemento de identidade. Cada vértice representa uma rotação em torno do eixo que aponta do centro para aquele vértice, por um ângulo igual à distância da origem, em radianos. Vértices no mesmo poliedro estão na mesma classe de conjugação. Como a equação da classe de conjugação para A 5 é 1 + 12 + 12 + 15 + 20 = 60 , obtemos quatro poliedros distintos (não triviais).
Os vértices de cada poliedro estão em correspondência bijetiva com os elementos de sua classe de conjugação, com exceção da classe de conjugação de (2,2) -ciclos, que é representada por um icosidodecaedro na superfície externa, com seus vértices antípodais identificados com uns aos outros. A razão para essa redundância é que as rotações correspondentes são por π radianos e, portanto, podem ser representadas por um vetor de comprimento π em qualquer uma das duas direções. Assim, a classe dos (2,2) -ciclos contém 15 elementos, enquanto o icosidodecaedro tem 30 vértices.
As duas classes de conjugação de doze 5-ciclos em A 5 são representadas por dois icosaedros, de raios 2 π / 5 e 4 π / 5, respectivamente. O automorfismo externo não trivial em Out (A 5 ) ≃ Z 2 troca essas duas classes e o icosaedra correspondente.
Exemplo: o quebra-cabeça 15
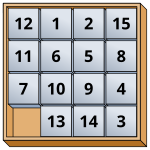
Pode-se provar que o quebra-cabeça 15 , famoso exemplo do quebra-cabeça deslizante , pode ser representado pelo grupo alternado A 15 , pois as combinações do quebra-cabeça 15 podem ser geradas por 3 ciclos . Na verdade, qualquer quebra-cabeça deslizante 2 k - 1 com ladrilhos quadrados de tamanho igual pode ser representado por A 2 k −1 .
Subgrupos
A 4 é o menor grupo demonstrando que o inverso do teorema de Lagrange não é verdadeiro em geral: dado um grupo finito G e um divisor d de | G |, não existe necessariamente um subgrupo de G de ordem d : o grupo G = A 4 , de ordem 12, não tem subgrupo de ordem 6. Um subgrupo de três elementos (gerado por uma rotação cíclica de três objetos) com qualquer elemento não trivial distinto gera o grupo inteiro.
Para todo n > 4 , A n não tem subgrupos normais não triviais (ou seja, adequados) . Assim, A n é um grupo simples para todo n > 4 . A 5 é o menor grupo não solucionável .
Homologia de grupo
A homologia de grupo dos grupos alternados exibe estabilização, como na teoria da homotopia estável : para n suficientemente grande , é constante. No entanto, há alguma homologia excepcional de baixa dimensão. Observe que a homologia do grupo simétrico exibe estabilização semelhante, mas sem as exceções de baixa dimensão (elementos de homologia adicionais).
H 1 : Abelianização
O primeiro grupo de homologia coincide com a abelianização , e (uma vez que A n é perfeito , exceto para as exceções citadas) é assim:
- H 1 (A n , Z) = Z 1 para n = 0, 1, 2;
-
H 1 (A 3 , Z) = A ab
3 = A 3 = Z 3 ; -
H 1 (A 4 , Z) = A ab
4 = Z 3 ; - H 1 (A n , Z) = Z 1 para n ≥ 5.
Isso é facilmente visto diretamente, como segue. A n é gerado por 3 ciclos - então os únicos mapas de abelianização não triviais são A n → Z 3 , uma vez que elementos de ordem 3 devem ser mapeados para elementos de ordem 3 - e para n ≥ 5 todos os 3 ciclos são conjugados, então eles devem mapear para o mesmo elemento na abelianização, uma vez que a conjugação é trivial em grupos abelianos. Assim, um ciclo de 3 como (123) deve mapear para o mesmo elemento que seu inverso (321), mas, portanto, deve mapear para a identidade, já que deve ter ordem dividindo 2 e 3, então a abelianização é trivial.
Para n <3 , A n é trivial e, portanto, tem abelianização trivial. Para A 3 e A 4 pode-se calcular a abelianização diretamente, observando que os 3 ciclos formam duas classes de conjugação (ao invés de serem todos conjugados) e há mapas não triviais A 3 ↠ Z 3 (na verdade, um isomorfismo) e A 4 ↠ Z 3 .
H 2 : multiplicadores de Schur
Os multiplicadores de Schur dos grupos alternados A n (no caso em que n é pelo menos 5) são os grupos cíclicos de ordem 2, exceto no caso em que n é 6 ou 7, caso em que também há uma cobertura tripla. Nestes casos, então, o multiplicador de Schur é (o grupo cíclico) de ordem 6. Eles foram calculados pela primeira vez em ( Schur 1911 ).
- H 2 (A n , Z) = Z 1 para n = 1, 2, 3;
- H 2 (A n , Z) = Z 2 para n = 4, 5;
- H 2 (A n , Z) = Z 6 para n = 6, 7;
- H 2 (A n , Z) = Z 2 para n ≥ 8.
Notas
Referências
- Robinson, Derek John Scott (1996), Um curso na teoria dos grupos , Textos de graduação em matemática, 80 (2 ed.), Springer, ISBN 978-0-387-94461-6
- Schur, Issai (1911), "Über die Darstellung der symmetrischen und der alternierenden Gruppe durch gebrochene lineare Substitutionen", Journal für die reine und angewandte Mathematik , 139 : 155-250, doi : 10.1515 / crll.1911.139.155
- Scott, WR (1987), Group Theory , Nova York: Dover Publications , ISBN 978-0-486-65377-8


