Sequência Farey - Farey sequence

Diagrama de Farey para F ₉ representado com arcos circulares. Na imagem SVG , passe o mouse sobre uma curva para destacá-la e seus termos.

Diagrama de Farey para F ₉ .

Padrão simétrico formado pelos denominadores da sequência de Farey, F ₉ .

Padrão simétrico formado pelos denominadores da sequência de Farey, F ₂₅ .

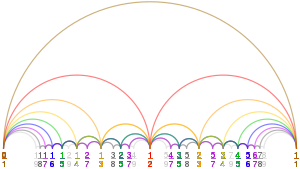
Em matemática , a sequência de Farey de ordem n é a sequência de frações totalmente reduzidas , seja entre 0 e 1, ou sem essa restrição, que quando em termos mais baixos têm denominadores menores ou iguais a n , dispostos em ordem crescente de tamanho.

Com a definição restrita, cada sequência Farey começa com o valor 0, denotado pela fração 0/1e termina com o valor 1, denotado pela fração 1/1 (embora alguns autores omitam esses termos).

Uma sequência Farey às vezes é chamada de série Farey , o que não é estritamente correto, porque os termos não são somados.

Exemplos

As sequências Farey das ordens 1 a 8 são:

F ₁ = {0/1_, 1/1 }

F ₂ = {0/1_, 1/2_, 1/1 }

F ₃ = {0/1_, 1/3_, 1/2_, 2/3_, 1/1 }

F ₄ = {0/1_, 1/4_, 1/3_, 1/2_, 2/3_, 3/4_, 1/1 }

F ₅ = {0/1_, 1/5_, 1/4_, 1/3_, 2/5_, 1/2_, 3/5_, 2/3_, 3/4_, 4/5_, 1/1 }

F ₆ = {0/1_, 1/6_, 1/5_, 1/4_, 1/3_, 2/5_, 1/2_, 3/5_, 2/3_, 3/4_, 4/5_, 5/6_, 1/1 }

F ₇ = {0/1_, 1/7_, 1/6_, 1/5_, 1/4_, 2/7_, 1/3_, 2/5_, 3/7_, 1/2_, 4/7_, 3/5_, 2/3_, 5/7_, 3/4_, 4/5_, 5/6_, 6/7_, 1/1 }

F ₈ = {0/1_, 1/8_, 1/7_, 1/6_, 1/5_, 1/4_, 2/7_, 1/3_, 3/8_, 2/5_, 3/7_, 1/2_, 4/7_, 3/5_, 5/8_, 2/3_, 5/7_, 3/4_, 4/5_, 5/6_, 6/7_, 7/8_, 1/1 }

 F1 = {0/1, 1/1}
 F2 = {0/1, 1/2, 1/1}
 F3 = {0/1, 1/3, 1/2, 2/3, 1/1}
 F4 = {0/1, 1/4, 1/3, 1/2, 2/3, 3/4, 1/1}
 F5 = {0/1, 1/5, 1/4, 1/3, 2/5, 1/2, 3/5, 2/3, 3/4, 4/5, 1/1}
 F6 = {0/1, 1/6, 1/5, 1/4, 1/3, 2/5, 1/2, 3/5, 2/3, 3/4, 4/5, 5/6 , 1/1}
 F7 = {0/1, 1/7, 1/6, 1/5, 1/4, 2/7, 1/3, 2/5, 3/7, 1/2, 4/7, 3/5 , 2/3, 5/7, 3/4, 4/5, 5/6, 6/7, 1/1}
 F8 = {0/1, 1/8, 1/7, 1/6, 1/5, 1/4, 2/7, 1/3, 3/8, 2/5, 3/7, 1/2 , 4/7, 3/5, 5/8, 2/3, 5/7, 3/4, 4/5, 5/6, 6/7, 7/8, 1/1}

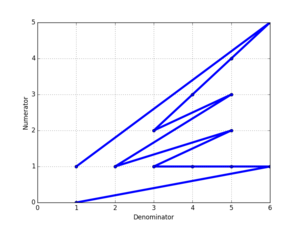
Plotar os numeradores em relação aos denominadores de uma sequência de Farey dá uma forma como a da direita, mostrada para F ₆ .

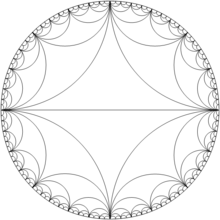
O reflexo dessa forma em torno dos eixos diagonais e principais gera o raio de sol de Farey , mostrado abaixo. O sunburst de Farey de ordem n conecta os pontos de grade inteiros visíveis da origem no quadrado do lado 2 n , centralizado na origem. Usando o teorema de Pick, a área da explosão solar é 4 (| F _n | −1), onde | F _n | é o número de frações em F _n .

História

A história da 'série Farey' é muito curiosa - Hardy & Wright (1979)

... mais uma vez o homem cujo nome foi dado a uma relação matemática não foi o descobridor original até onde vão os registros. - Beiler (1964)

As sequências de Farey têm o nome do geólogo britânico John Farey, Sr. , cuja carta sobre essas sequências foi publicada na Philosophical Magazine em 1816. Farey conjecturou, sem oferecer provas, que cada novo termo em uma expansão da sequência de Farey é o mediante de seus vizinhos . A carta de Farey foi lida por Cauchy , que forneceu uma prova em seus Exercices de mathématique , e atribuiu esse resultado a Farey. Na verdade, outro matemático, Charles Haros , publicou resultados semelhantes em 1802, que não eram conhecidos nem por Farey nem por Cauchy. Portanto, foi um acidente histórico que ligou o nome de Farey a essas sequências. Este é um exemplo da lei da epônima de Stigler .

Propriedades

Comprimento da sequência e índice de uma fração

A sequência Farey de ordem n contém todos os membros das sequências Farey de ordens inferiores. Em particular, F _n contém todos os membros de F _{n −1} e também contém uma fração adicional para cada número menor que n e coprime para n . Assim, F ₆ consiste em F ₅ junto com as frações1/6 e 5/6.

O meio termo de uma sequência Farey F _n é sempre1/2, para n > 1. A partir disso, podemos relacionar os comprimentos de F _n e F _{n −1} usando a função totiente de Euler  : ${\ displaystyle \ varphi (n)}$

${\ displaystyle | F_ {n} | = | F_ {n-1} | + \ varphi (n).}$

Usando o fato de que | F ₁ | = 2, podemos derivar uma expressão para o comprimento de F _n :

${\ displaystyle | F_ {n} | = 1 + \ sum _ {m = 1} ^ {n} \ varphi (m) = 1 + \ Phi (n),}$

onde está o totiente sumatório . ${\ displaystyle \ Phi (n)}$

Nos tambem temos :

${\ displaystyle | F_ {n} | = {\ frac {1} {2}} \ left (3+ \ sum _ {d = 1} ^ {n} \ mu (d) \ left \ lfloor {\ tfrac { n} {d}} \ right \ rfloor ^ {2} \ right),}$

e por uma fórmula de inversão de Möbius  :

${\ displaystyle | F_ {n} | = {\ frac {1} {2}} (n + 3) n- \ sum _ {d = 2} ^ {n} | F _ {\ lfloor n / d \ rfloor} |,}$

onde µ ( d ) é a função de Möbius teórica numérica e é a função de piso . ${\ displaystyle \ lfloor {\ tfrac {n} {d}} \ rfloor}$

O comportamento assintótico de | F _n | é :

${\ displaystyle | F_ {n} | \ sim {\ frac {3n ^ {2}} {\ pi ^ {2}}}.}$

O índice de uma fração na sequência de Farey é simplesmente a posição que ocupa na sequência. Isso é de especial relevância, pois é usado em uma formulação alternativa da hipótese de Riemann , veja abaixo . Seguem várias propriedades úteis: ${\ displaystyle I_ {n} (a_ {k, n}) = k}$${\ displaystyle a_ {k, n}}$${\ displaystyle F_ {n} = \ {a_ {k, n}: k = 0,1, \ ldots, m_ {n} \}}$${\ displaystyle a_ {k, n}}$

${\ displaystyle I_ {n} (0/1) = 0,}$

${\ displaystyle I_ {n} (1 / n) = 1,}$

${\ displaystyle I_ {n} (1/2) = (| F_ {n} | -1) / 2,}$

${\ displaystyle I_ {n} (1/1) = | F_ {n} | -1,}$

${\ displaystyle I_ {n} (h / k) = | F_ {n} | -1-I_ {n} ((kh) / k).}$

O índice de onde e é o mínimo múltiplo comum dos primeiros números,, é dado por: ${\ displaystyle 1 / k}$${\ displaystyle n / (i + 1) <k \ leq n / i}$${\ displaystyle n}$${\ displaystyle i}$${\ displaystyle n = {\ rm {lcm}} ([2, i])}$

${\ displaystyle I_ {n} (1 / k) = 1 + n \ sum _ {j = 1} ^ {i} {\ frac {\ varphi (j)} {j}} - k \ Phi (i). }$

Vizinhos baratos

As frações que são termos vizinhos em qualquer sequência de Farey são conhecidas como par de Farey e têm as seguintes propriedades.

Se uma/b e c/d são vizinhos em uma sequência de Farey, com uma/b < c/d, então a diferença deles c/d - uma/b é igual a 1/bd. Isso ocorre porque cada par consecutivo de racionais de Farey tem uma área equivalente a 1.

Se r1 = p / q e r2 = p '/ q' são interpretados como vetores (p, q) no plano x, y, a área de A (p / q, p '/ q') é dada por qp ' - q'p. Como qualquer fração adicionada entre duas frações de sequência de Farey consecutivas anteriores é calculada como a mediante (⊕)

A (r1, r1⊕r2) = A (r1, r1) + A (r1, r2) = A (r1, r2) = 1 (uma vez que r1 = 1/0 e r2 = 0/1, sua área deve ser um) .

Desde:${\ displaystyle {\ frac {c} {d}} - {\ frac {a} {b}} = {\ frac {bc-ad} {bd}},}$

isso é equivalente a dizer que

${\ displaystyle bc-ad = 1}$.

Desse modo 1/3 e 2/5são vizinhos em F ₅ , e sua diferença é1/15.

O inverso também é verdadeiro. Se

${\ displaystyle bc-ad = 1}$

para inteiros positivos a , b , c e d com a < b e c < d entãouma/b e c/dserão vizinhos na sequência de Farey de ordem max ( b, d ).

Se p/q tem vizinhos uma/b e c/d em alguma sequência de Farey, com

${\ displaystyle {\ frac {a} {b}} <{\ frac {p} {q}} <{\ frac {c} {d}}}$

então p/qé o mediante deuma/b e c/d - em outras palavras,

${\ displaystyle {\ frac {p} {q}} = {\ frac {a + c} {b + d}}.}$

Isso segue facilmente da propriedade anterior, uma vez que se bp - aq = qc - pd = 1 , então bp + pd = qc + aq , p ( b + d ) = q ( a + c ) ,p/q = a + c/b + d.

Segue-se que se uma/b e c/d são vizinhos em uma sequência Farey, então o primeiro termo que aparece entre eles conforme a ordem da sequência Farey é incrementada é

${\ displaystyle {\ frac {a + c} {b + d}},}$

que aparece pela primeira vez na sequência de Farey de ordem b + d .

Assim, o primeiro termo a aparecer entre 1/3 e 2/5 é 3/8, que aparece em F ₈ .

O número total de pares de vizinhos Farey em F _n é 2 | F _n | -3.

A árvore Stern-Brocot é uma estrutura de dados que mostra como a sequência é construída a partir de 0 (=0/1) e 1 (= 1/1), tomando mediantes sucessivos.

Vizinhos baratos e frações contínuas

As frações que aparecem como vizinhas em uma sequência de Farey têm expansões de fração contínuas estreitamente relacionadas . Cada fração tem duas expansões de fração contínuas - em uma, o termo final é 1; no outro, o prazo final é maior que 1. Sep/q, que aparece pela primeira vez na sequência de Farey F _q , tem expansões de fração contínuas

[0; a ₁ , a ₂ , ..., a _{n - 1} , a _n , 1]

[0; a ₁ , a ₂ , ..., a _{n - 1} , a _n + 1]

então o vizinho mais próximo de p/qem F _q (que será seu vizinho com o maior denominador) tem uma expansão de fração contínua

[0; a ₁ , a ₂ , ..., a _n ]

e seu outro vizinho tem uma expansão contínua da fração

[0; a ₁ , a ₂ , ..., a _{n - 1} ]

Por exemplo, 3/8tem as duas expansões de fração contínuas [0; 2, 1, 1, 1] e [0; 2, 1, 2] , e seus vizinhos em F ₈ são2/5, que pode ser expandido como [0; 2, 1, 1] ; e1/3, que pode ser expandido como [0; 2, 1] .

Farey frações e o mínimo múltiplo comum

O lcm pode ser expresso como os produtos das frações Farey como

${\ displaystyle {\ text {lcm}} [1,2, ..., N] = e ^ {\ psi (N)} = {\ frac {1} {2}} \ left (\ prod _ {r \ in F_ {N}, 0 <r \ leq 1/2} 2 \ sin (\ pi r) \ right) ^ {2}}$

onde está a segunda função Chebyshev . ${\ displaystyle \ psi (N)}$

Frações frágeis e o maior divisor comum

Uma vez que a função totiente de Euler está diretamente conectada ao mdc , o número de elementos em F _{n também está} ,

${\ displaystyle | F_ {n} | = 1 + \ sum _ {m = 1} ^ {n} \ varphi (m) = 1 + \ sum \ limits _ {m = 1} ^ {n} \ sum \ limites _ {k = 1} ^ {m} \ gcd (k, m) \ cos {2 \ pi {\ frac {k} {m}}}.}$

Para quaisquer 3 frações tarifárias uma/b, c/d e e/fa seguinte identidade entre os mdc dos determinantes da matriz 2x2 em valor absoluto é válida:

${\ displaystyle \ gcd \ left ({\ begin {Vmatrix} a & c \\ b & d \ end {Vmatrix}}, {\ begin {Vmatrix} a & e \\ b & f \ end {Vmatrix}} \ right) = \ gcd \ left ( {\ begin {Vmatrix} a & c \\ b & d \ end {Vmatrix}}, {\ begin {Vmatrix} c & e \\ d & f \ end {Vmatrix}} \ right) = \ gcd \ left ({\ begin {Vmatrix} a & e \ \ b & f \ end {Vmatrix}}, {\ begin {Vmatrix} c & e \\ d & f \ end {Vmatrix}} \ right)}$

Formulários

As sequências Farey são muito úteis para encontrar aproximações racionais de números irracionais. Por exemplo, a construção por Eliahou de um limite inferior no comprimento de ciclos não triviais no processo 3 x +1 usa sequências de Farey para calcular uma expansão de fração contínua do número log ₂ (3).

Em sistemas físicos com fenômenos de ressonância, as sequências de Farey fornecem um método muito elegante e eficiente para calcular localizações de ressonância em 1D e 2D.

As sequências de Farey são proeminentes em estudos de planejamento de caminhos de qualquer ângulo em grades de células quadradas, por exemplo, na caracterização de sua complexidade computacional ou otimização. A conexão pode ser considerada em termos de caminhos restritos por r , ou seja, caminhos feitos de segmentos de linha que atravessam no máximo linhas e no máximo colunas de células. Let É o conjunto de vetores de tal forma que , e , são primos entre si. Deixe ser o resultado de refletir na linha . Deixe . Então, qualquer caminho restrito por r pode ser descrito como uma sequência de vetores de . Há uma bijeção entre e a sequência de ordem de Farey dada pelo mapeamento de . ${\ displaystyle r}$${\ displaystyle r}$${\ displaystyle Q}$${\ displaystyle (q, p)}$${\ displaystyle 1 \ leq q \ leq r}$${\ displaystyle 0 \ leq p \ leq q}$${\ displaystyle p}$${\ displaystyle q}$${\ displaystyle Q *}$${\ displaystyle Q}$${\ displaystyle y = x}$${\ displaystyle S = \ {(\ pm x, \ pm y) :( x, y) \ in Q \ cup Q * \}}$${\ displaystyle S}$${\ displaystyle Q}$${\ displaystyle r}$${\ displaystyle (q, p)}$${\ displaystyle {\ tfrac {p} {q}}}$

Círculos de Ford

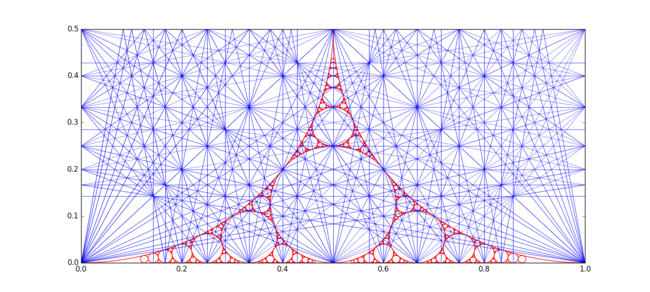
Comparação de círculos de Ford e um diagrama de Farey com arcos circulares para n de 1 a 9. Cada arco intercepta seus círculos correspondentes em ângulos retos. Na imagem SVG , passe o mouse sobre um círculo ou curva para destacá-lo e seus termos.

Há uma conexão entre a sequência de Farey e os círculos de Ford .

Para cada fração p/q (em seus termos mais baixos) existe um círculo Ford C [p/q], que é o círculo com raio 1 / (2 q ² ) e centro em (p/q, 1/ 2 q ² ) Dois círculos Ford para frações diferentes são disjuntos ou tangentes um ao outro - dois círculos Ford nunca se cruzam. Se 0 <p/q <1 então os círculos de Ford que são tangentes a C [p/q] são precisamente os círculos da Ford para frações vizinhas de p/q em alguma sequência de Farey.

Assim, C [2/5] é tangente a C [1/2], C [1/3], C [3/7], C [3/8] etc.

Os círculos de Ford aparecem também na junta apolínea (0,0,1,1). A imagem abaixo ilustra isso junto com as linhas de ressonância de Farey.

Junta apolínea (0,0,1,1) e o diagrama de ressonância de Farey.

Hipótese de Riemann

As sequências de Farey são usadas em duas formulações equivalentes da hipótese de Riemann . Suponha que os termos de são . Definir , em outras palavras, é a diferença entre o k- ésimo termo da n- ésima seqüência de Farey, e o k- ésimo membro de um conjunto de mesmo número de pontos, distribuídos uniformemente no intervalo unitário. Em 1924 Jérôme Franel provou que a declaração ${\ displaystyle F_ {n}}$${\ displaystyle \ {a_ {k, n}: k = 0,1, \ ldots, m_ {n} \}}$${\ displaystyle d_ {k, n} = a_ {k, n} -k / m_ {n}}$${\ displaystyle d_ {k, n}}$

${\ displaystyle \ sum _ {k = 1} ^ {m_ {n}} d_ {k, n} ^ {2} = O (n ^ {r}) \ quad \ forall r> -1}$

é equivalente à hipótese de Riemann, e então Edmund Landau observou (logo após o artigo de Franel) que a declaração

${\ displaystyle \ sum _ {k = 1} ^ {m_ {n}} | d_ {k, n} | = O (n ^ {r}) \ quad \ forall r> 1/2}$

também é equivalente à hipótese de Riemann.

Outras somas envolvendo frações tarifárias

A soma de todas as frações Farey de ordem n é a metade do número de elementos:

${\ displaystyle \ sum _ {r \ in F_ {n}} r = {\ frac {1} {2}} | F_ {n} |.}$

A soma dos denominadores na sequência de Farey é duas vezes a soma dos numeradores e está relacionada à função totiente de Euler:

${\ displaystyle \ sum _ {a / b \ in F_ {n}} b = 2 \ sum _ {a / b \ in F_ {n}} a = 1 + \ sum _ {i = 1} ^ {n} i \ varphi (i),}$

que foi conjecturado por Harold L. Aaron em 1962 e demonstrado por Jean A. Blake em 1966. Uma prova de uma linha da conjectura de Harold L. Aaron é a seguinte. A soma dos numeradores é . A soma dos denominadores é . O quociente da primeira soma pela segunda soma é . ${\ displaystyle {\ displaystyle 1+ \ sum _ {2 \ leq b \ leq n} \ sum _ {(a, b) = 1} a = 1 + \ sum _ {2 \ leq b \ leq n} b { \ frac {\ varphi (b)} {2}}}}$${\ displaystyle {\ displaystyle 2+ \ sum _ {2 \ leq b \ leq n} \ sum _ {(a, b) = 1} b = 2 + \ sum _ {2 \ leq b \ leq n} b \ varphi (b)}}$${\ displaystyle {\ frac {1} {2}}}$

Sejam b _j os denominadores ordenados de F _n , então:

${\ displaystyle \ sum _ {j = 0} ^ {| F_ {n} | -1} {\ frac {b_ {j}} {b_ {j + 1}}} = {\ frac {3 | F_ {n } | -4} {2}}}$

e

${\ displaystyle \ sum _ {j = 0} ^ {| F_ {n} | -1} {\ frac {1} {b_ {j + 1} b_ {j}}} = 1.}$

Seja a _j / b _j a _j -ésima fração de Farey em F _n , então

${\ displaystyle \ sum _ {j = 1} ^ {| F_ {n} | -1} (a_ {j-1} b_ {j + 1} -a_ {j + 1} b_ {j-1}) = \ sum _ {j = 1} ^ {| F_ {n} | -1} {\ begin {Vmatrix} a_ {j-1} & a_ {j + 1} \\ b_ {j-1} & b_ {j + 1 } \ end {Vmatrix}} = 3 (| F_ {n} | -1) -2n-1,}$

que é demonstrado em. Também de acordo com esta referência, o termo dentro da soma pode ser expresso de muitas maneiras diferentes:

${\ displaystyle a_ {j-1} b_ {j + 1} -a_ {j + 1} b_ {j-1} = {\ frac {b_ {j-1} + b_ {j + 1}} {b_ { j}}} = {\ frac {a_ {j-1} + a_ {j + 1}} {a_ {j}}} = \ left \ lfloor {\ frac {n + b_ {j-1}} {b_ {j}}} \ right \ rfloor,}$

obtendo assim muitas somas diferentes sobre os elementos Farey com o mesmo resultado. Usando a simetria em torno de 1/2, a soma anterior pode ser limitada à metade da sequência como

${\ displaystyle \ sum _ {j = 1} ^ {\ lfloor | F_ {n} | / 2 \ rfloor} (a_ {j-1} b_ {j + 1} -a_ {j + 1} b_ {j- 1}) = 3 (| F_ {n} | -1) / 2-n- \ lceil n / 2 \ rceil,}$

A função Mertens pode ser expressa como uma soma sobre as frações Farey como

${\ displaystyle M (n) = - 1+ \ sum _ {a \ in {\ mathcal {F}} _ {n}} e ^ {2 \ pi ia}}$   onde     está a seqüência de Farey de ordem n .${\ displaystyle {\ mathcal {F}} _ {n}}$

Esta fórmula é usada na demonstração do teorema de Franel – Landau .

Próximo termo

Um algoritmo surpreendentemente simples existe para gerar os termos de F _n na ordem tradicional (crescente) ou na ordem não tradicional (decrescente). O algoritmo calcula cada entrada sucessiva em termos das duas entradas anteriores usando a propriedade mediante fornecida acima. Seuma/b e c/d são as duas entradas fornecidas, e p/q é a próxima entrada desconhecida, então c/d = a  +  p/b  +  q. Desdec/dé menor em termos, deve haver um número inteiro k tal que kc  =  um  +  P e KD  =  b  +  q , dando p  =  kc  -  um e q  =  kd  -  b . Se considerarmos p e q ser funções de k , em seguida,

${\ displaystyle {\ frac {p (k)} {q (k)}} - {\ frac {c} {d}} = {\ frac {cb-da} {d (kd-b)}}}$

então quanto maior k fica, mais pertop/q chega a c/d.

Para dar o próximo termo na sequência, k deve ser o maior possível, sujeito a kd  -  b  ≤  n (já que estamos considerando apenas números com denominadores não maiores que n ), então k é o maior inteiro ≤ n  +  b/d. Colocando este valor de k de volta nas equações para p e q dá

${\ displaystyle p = \ left \ lfloor {\ frac {n + b} {d}} \ right \ rfloor ca}$

${\ displaystyle q = \ left \ lfloor {\ frac {n + b} {d}} \ right \ rfloor db}$

Isso é implementado em Python da seguinte maneira:

def farey_sequence(n: int, descending: bool = False) -> None:
    """Print the n'th Farey sequence. Allow for either ascending or descending."""
    (a, b, c, d) = (0, 1, 1, n)
    if descending:
        (a, c) = (1, n - 1)
    print("{0}/{1}".format(a, b))
    while (c <= n and not descending) or (a > 0 and descending):
        k = (n + b) // d
        (a, b, c, d) = (c, d, k * c - a, k * d - b)
        print("{0}/{1}".format(a, b))

As buscas de força bruta por soluções para equações diofantinas em racionais podem freqüentemente tirar vantagem da série de Farey (para pesquisar apenas formas reduzidas). As linhas marcadas com (*) também podem ser modificadas para incluir quaisquer dois termos adjacentes de modo a gerar termos apenas maiores (ou menores) do que um determinado termo.

Veja também

• Padrão ABACABA
• Árvore Stern-Brocot
• Função totiente de Euler

Notas de rodapé

Referências

Leitura adicional

• Hatcher, Allen . “Topologia de Números” . Matemática. Ithaca, NY: Cornell U.
• Graham, Ronald L .; Knuth, Donald E .; Patashnik, Oren (1989). Concrete Mathematics: A Foundation for Computer Science (2ª ed.). Boston, MA: Addison-Wesley. pp. 115–123, 133–139, 150, 462–463, 523–524. ISBN 0-201-55802-5. - em particular, consulte §4.5 (pp. 115–123), Bonus Problem 4.61 (pp. 150, 523–524), §4.9 (pp. 133–139), §9.3, Problema 9.3.6 (pp. 462– 463).
• Vepstas, Linas. "O ponto de interrogação de Minkowski, GL (2, Z) e o grupo modular" (PDF) . - analisa os isomorfismos da Árvore Stern-Brocot.
• Vepstas, Linas. "Simetrias de mapas de duplicação de período" (PDF) . - analisa as conexões entre as frações de Farey e os fractais.
• Cobeli, Cristian; Zaharescu, Alexandru (2003). "A sequência Haros-Farey aos duzentos anos. Um levantamento". Acta Univ. Apulensis Math. Informar. (5): 1–38. "pp. 1-20" (PDF) . Acta Univ. Apulensis . "pp. 21–38" (PDF) . Acta Univ. Apulensis .
• Matveev, Andrey O. (2017). Sequências Farey: Dualidade e Mapas Entre Subsequências . Berlim, DE: De Gruyter. ISBN 978-3-11-054662-0.

links externos

• Bogomolny, Alexander . "Série Farey" . Corte o nó .
• Bogomolny, Alexander . "Árvore Stern-Brocot" . Corte o nó .
• Pennestri, Ettore. "Uma mesa Brocot de base 120" .
• "Farey series" , Encyclopedia of Mathematics , EMS Press , 2001 [1994]
• Weisstein, Eric W. "Stern-Brocot Tree" . MathWorld .
• Sequência OEIS A005728 (Número de frações na série Farey de ordem n)
• Sequência OEIS A006842 (Numeradores da série Farey de ordem n)
• Sequência OEIS A006843 (Denominadores da série Farey de ordem n)
• Bonahon, Francis . Frações engraçadas e círculos de Ford (vídeo). Brady Haran . Obtido em 9 de junho de 2015 - via YouTube.