Processo Gaussiano - Gaussian process

Em teoria de probabilidade e estatística , um processo gaussiano é um processo estocástico (uma coleção de variáveis aleatórias indexadas por tempo ou espaço), de modo que toda coleção finita dessas variáveis aleatórias tem uma distribuição normal multivariada , ou seja, toda combinação linear finita delas é normalmente distribuído. A distribuição de um processo gaussiano é a distribuição conjunta de todas aquelas (infinitamente muitas) variáveis aleatórias e, como tal, é uma distribuição sobre funções com um domínio contínuo, por exemplo, tempo ou espaço.

O conceito de processos gaussianos tem o nome de Carl Friedrich Gauss porque se baseia na noção de distribuição gaussiana ( distribuição normal ). Os processos gaussianos podem ser vistos como uma generalização infinita dimensional de distribuições normais multivariadas.

Os processos gaussianos são úteis na modelagem estatística , beneficiando-se de propriedades herdadas da distribuição normal. Por exemplo, se um processo aleatório é modelado como um processo gaussiano, as distribuições de várias quantidades derivadas podem ser obtidas explicitamente. Essas quantidades incluem o valor médio do processo em um intervalo de tempos e o erro na estimativa da média usando valores de amostra em um pequeno conjunto de tempos. Embora os modelos exatos muitas vezes sejam escalonados de maneira inadequada à medida que a quantidade de dados aumenta, vários métodos de aproximação foram desenvolvidos, os quais geralmente mantêm uma boa precisão enquanto reduzem drasticamente o tempo de computação.

Definição

Um processo estocástico contínuo no tempo é gaussiano se e somente se para cada conjunto finito de índices no conjunto de índices ${\ displaystyle \ left \ {X_ {t}; t \ in T \ right \}}$ ${\ displaystyle t_ {1}, \ ldots, t_ {k}}$ ${\ displaystyle T}$

{\ displaystyle \ mathbf {X} _ {t_ {1}, \ ldots, t_ {k}} = (X_ {t_ {1}}, \ ldots, X_ {t_ {k}})}

é uma variável aleatória gaussiana multivariada . Isso é o mesmo que dizer que cada combinação linear de tem uma distribuição normal univariada (ou gaussiana). ${\ displaystyle (X_ {t_ {1}}, \ ldots, X_ {t_ {k}})}$

Usando funções características de variáveis aleatórias, a propriedade gaussiana pode ser formulada da seguinte forma: é gaussiana se e somente se, para cada conjunto finito de índices , houver valores reais , com tal que a seguinte igualdade seja válida para todos ${\ displaystyle \ left \ {X_ {t}; t \ in T \ right \}}$ ${\ displaystyle t_ {1}, \ ldots, t_ {k}}$ ${\ displaystyle \ sigma _ {\ ell j}}$ ${\ displaystyle \ mu _ {\ ell}}$ ${\ displaystyle \ sigma _ {jj}> 0}$ ${\ displaystyle s_ {1}, s_ {2}, \ ldots, s_ {k} \ in \ mathbb {R}}$

{\ displaystyle \ operatorname {E} \ left (\ exp \ left (i \ \ sum _ {\ ell = 1} ^ {k} s _ {\ ell} \ \ mathbf {X} _ {t _ {\ ell}} \ right) \ right) = \ exp \ left (- {\ frac {1} {2}} \, \ sum _ {\ ell, j} \ sigma _ {\ ell j} s _ {\ ell} s_ {j } + i \ sum _ {\ ell} \ mu _ {\ ell} s _ {\ ell} \ right)}

.

onde denota a unidade imaginária tal que . ${\ displaystyle i}$ ${\ displaystyle i ^ {2} = - 1}$

Os números e podem ser as covariâncias e as médias das variáveis no processo. ${\ displaystyle \ sigma _ {\ ell j}}$ ${\ displaystyle \ mu _ {\ ell}}$

Variância

A variância de um processo gaussiano é finita a qualquer momento , formalmente ${\ displaystyle t}$

{\ displaystyle \ operatorname {var} [X (t)] = \ operatorname {E} [| X (t) - \ operatorname {E} [X (t)] | ^ {2}] <\ infty \ quad { \ text {para todos}} t \ em T}

.

Estacionariedade

Para processos estocásticos gerais, a estacionariedade no sentido estrito implica a estacionariedade no sentido amplo, mas nem todo processo estocástico estacionário no sentido amplo é estacionário no sentido estrito. No entanto, para um processo estocástico gaussiano, os dois conceitos são equivalentes.

Um processo estocástico gaussiano é estacionário em senso estrito se, e somente se, for estacionário em senso amplo.

Exemplo

Há uma representação explícita para processos gaussianos estacionários. Um exemplo simples desta representação é

{\ displaystyle X_ {t} = \ cos (arroba) \ xi _ {1} + \ sin (arroba) \ xi _ {2}}

onde e são variáveis aleatórias independentes com a distribuição normal padrão . ${\ displaystyle \ xi _ {1}}$ ${\ displaystyle \ xi _ {2}}$

Funções de covariância

Um fato chave dos processos gaussianos é que eles podem ser completamente definidos por suas estatísticas de segunda ordem. Assim, se um processo gaussiano é assumido como tendo média zero, definir a função de covariância define completamente o comportamento do processo. É importante ressaltar que a definição não negativa desta função permite sua decomposição espectral usando a expansão de Karhunen-Loève . Aspectos básicos que podem ser definidos através da função de covariância são a estacionariedade , isotropia , suavidade e periodicidade do processo .

A estacionariedade se refere ao comportamento do processo em relação à separação de quaisquer dois pontos e . Se o processo é estacionário, depende de sua separação, enquanto se não estacionário depende da posição real dos pontos e . Por exemplo, o caso especial de um processo Ornstein-Uhlenbeck , um processo de movimento browniano , é estacionário. ${\ displaystyle x}$ ${\ displaystyle x '}$ ${\ displaystyle x-x '}$ ${\ displaystyle x}$ ${\ displaystyle x '}$

Se o processo depender apenas da distância euclidiana (não da direção) entre e , então o processo é considerado isotrópico. Um processo simultaneamente estacionário e isotrópico é considerado homogêneo ; na prática, essas propriedades refletem as diferenças (ou melhor, a falta delas) no comportamento do processo dada a localização do observador. ${\ displaystyle | x-x '|}$ ${\ displaystyle x}$ ${\ displaystyle x '}$

Em última análise, os processos gaussianos se traduzem como priorizando as funções e a suavidade dessas prioridades pode ser induzida pela função de covariância. Se esperarmos que para os pontos de entrada "próximos" e seus pontos de saída correspondentes e também para os pontos de entrada "próximos", então a suposição de continuidade está presente. Se quisermos permitir um deslocamento significativo, podemos escolher uma função de covariância mais grosseira. Exemplos extremos do comportamento são a função de covariância de Ornstein-Uhlenbeck e o exponencial ao quadrado, onde o primeiro nunca é diferenciável e o último infinitamente diferenciável. ${\ displaystyle x}$ ${\ displaystyle x '}$ ${\ displaystyle y}$ ${\ displaystyle y '}$

Periodicidade se refere à indução de padrões periódicos no comportamento do processo. Formalmente, isso é obtido mapeando a entrada para um vetor bidimensional . ${\ displaystyle x}$ ${\ displaystyle u (x) = \ left (\ cos (x), \ sin (x) \ right)}$

Funções usuais de covariância

O efeito da escolha de diferentes kernels na distribuição de funções anteriores do processo Gaussiano. A esquerda é um kernel exponencial ao quadrado. O meio é browniano. A direita é quadrática.

Existem várias funções de covariância comuns:

Constante: ${\ displaystyle K _ {\ operatorname {C}} (x, x ') = C}$
Linear: ${\ displaystyle K _ {\ operatorname {L}} (x, x ') = x ^ {T} x'}$
ruído gaussiano branco: ${\ displaystyle K _ {\ operatorname {GN}} (x, x ') = \ sigma ^ {2} \ delta _ {x, x'}}$
Exponencial ao quadrado: ${\ displaystyle K _ {\ operatorname {SE}} (x, x ') = \ exp {\ Big (} - {\ frac {| d | ^ {2}} {2 \ ell ^ {2}}} {\ Grande )}}$
Ornstein – Uhlenbeck: ${\ displaystyle K _ {\ operatorname {OU}} (x, x ') = \ exp \ left (- {\ frac {| d |} {\ ell}} \ right)}$
Matérn: ${\ displaystyle K _ {\ operatorname {Matern}} (x, x ') = {\ frac {2 ^ {1- \ nu}} {\ Gamma (\ nu)}} {\ Big (} {\ frac {{ \ sqrt {2 \ nu}} | d |} {\ ell}} {\ Grande)} ^ {\ nu} K _ {\ nu} {\ Grande (} {\ frac {{\ sqrt {2 \ nu}} | d |} {\ ell}} {\ Big)}}$
Periódico: ${\ displaystyle K _ {\ operatorname {P}} (x, x ') = \ exp \ left (- {\ frac {2 \ sin ^ {2} \ left ({\ frac {d} {2}} \ right )} {\ ell ^ {2}}} \ right)}$
Quadrático Racional: ${\ displaystyle K _ {\ operatorname {RQ}} (x, x ') = (1+ | d | ^ {2}) ^ {- \ alpha}, \ quad \ alpha \ geq 0}$

Aqui . O parâmetro é a escala de comprimento característica do processo (praticamente, "quão próximos" dois pontos e têm que estar para se influenciarem significativamente), é o delta de Kronecker e o desvio padrão das flutuações de ruído. Além disso, é a função de Bessel modificada de ordem e é a função gama avaliada em . É importante ressaltar que uma função de covariância complicada pode ser definida como uma combinação linear de outras funções de covariância mais simples, a fim de incorporar diferentes percepções sobre o conjunto de dados em questão. ${\ displaystyle d = x-x '}$ ${\ displaystyle \ ell}$ ${\ displaystyle x}$ ${\ displaystyle x '}$ ${\ displaystyle \ delta}$ ${\ displaystyle \ sigma}$ ${\ displaystyle K _ {\ nu}}$ ${\ displaystyle \ nu}$ ${\ displaystyle \ Gamma (\ nu)}$ ${\ displaystyle \ nu}$

Claramente, os resultados inferenciais dependem dos valores dos hiperparâmetros (por exemplo, e ) que definem o comportamento do modelo. Uma escolha popular para é fornecer estimativas máximas a posteriori (MAP) dele com alguns escolhidos a priori. Se o prior for quase uniforme, isso equivale a maximizar a probabilidade marginal do processo; a marginalização sendo feita sobre os valores de processo observados . Essa abordagem também é conhecida como máxima verossimilhança II , maximização de evidências ou Bayes empírica . ${\ displaystyle \ theta}$ ${\ displaystyle \ ell}$ ${\ displaystyle \ sigma}$ ${\ displaystyle \ theta}$ ${\ displaystyle y}$

Continuidade

Para um processo gaussiano, a continuidade na probabilidade é equivalente à continuidade do quadrado médio , e a continuidade com a probabilidade um é equivalente à continuidade da amostra . O último implica, mas não está implícito por, continuidade na probabilidade. A continuidade na probabilidade é mantida se e somente se a média e a autocovariância forem funções contínuas. Em contraste, a continuidade da amostra foi desafiadora mesmo para processos gaussianos estacionários (como provavelmente notado primeiro por Andrey Kolmogorov ), e mais desafiadora para processos mais gerais. Como de costume, por processo contínuo de amostra entende-se um processo que admite modificação contínua de amostra .

Maleta estacionária

Para um processo gaussiano estacionário, algumas condições em seu espectro são suficientes para a continuidade da amostra, mas deixam de ser necessárias. Uma condição necessária e suficiente, às vezes chamada de teorema de Dudley-Fernique, envolve a função definida por ${\ displaystyle X = (X_ {t}) _ {t \ in \ mathbb {R}},}$ ${\ displaystyle \ sigma}$

{\ displaystyle \ sigma (h) = {\ sqrt {\ mathbb {E} {\ big (} X (t + h) -X (t) {\ big)} ^ {2}}}}

(o lado direito não depende devido à estacionariedade). Continuidade de em probabilidade é equivalente a continuidade de em Quando a convergência de para (as ) é muito lenta, a continuidade da amostra de pode falhar. A convergência das seguintes questões integrais: ${\ displaystyle t}$ ${\ displaystyle X}$ ${\ displaystyle \ sigma}$ ${\ displaystyle 0.}$ ${\ displaystyle \ sigma (h)}$ ${\ displaystyle 0}$ ${\ displaystyle h \ a 0}$ ${\ displaystyle X}$

{\ displaystyle I (\ sigma) = \ int _ {0} ^ {1} {\ frac {\ sigma (h)} {h {\ sqrt {\ log (1 / h)}}}} \, dh = \ int _ {0} ^ {\ infty} 2 \ sigma (\ mathbb {e} ^ {- x ^ {2}}) \, dx,}

essas duas integrais sendo iguais de acordo com a integração por substituição. O primeiro integrando não precisa ser limitado, pois assim a integral pode convergir ( ) ou divergir ( ). Tomando por exemplo o grande, isto é, o pequeno obtém-se quando e quando. Nestes dois casos, a função está aumentando, mas geralmente não é. Além disso, a condição ${\ displaystyle h = \ mathbb {e} ^ {- x ^ {2}},}$ ${\ displaystyle \ textstyle x = {\ sqrt {\ log (1 / h)}}.}$ ${\ displaystyle h \ a 0+,}$ ${\ displaystyle I (\ sigma) <\ infty}$ ${\ displaystyle I (\ sigma) = \ infty}$ ${\ displaystyle \ sigma (\ mathbb {e} ^ {- x ^ {2}}) = {\ tfrac {1} {x ^ {a}}}}$ ${\ displaystyle x,}$ ${\ displaystyle \ sigma (h) = (\ log (1 / h)) ^ {- a / 2}}$ ${\ displaystyle h,}$ ${\ displaystyle I (\ sigma) <\ infty}$ ${\ displaystyle a> 1,}$ ${\ displaystyle I (\ sigma) = \ infty}$ ${\ displaystyle 0 <a \ leq 1.}$ ${\ displaystyle \ sigma}$ ${\ displaystyle [0, \ infty),}$

{\ displaystyle (*)}

existe tal que é monótono

{\ displaystyle \ varepsilon> 0}

{\ displaystyle \ sigma}

{\ displaystyle [0, \ varepsilon]}

não decorre da continuidade e das relações evidentes (para todos ) e ${\ displaystyle \ sigma}$ ${\ displaystyle \ sigma (h) \ geq 0}$ ${\ displaystyle h}$ ${\ displaystyle \ sigma (0) = 0.}$

Teorema 1. Seja contínuo e satisfatório Então a condição é necessária e suficiente para a continuidade da amostra de ${\ displaystyle \ sigma}$ ${\ displaystyle (*).}$ ${\ displaystyle I (\ sigma) <\ infty}$ ${\ displaystyle X.}$

Alguma história. A suficiência foi anunciada por Xavier Fernique em 1964, mas a primeira prova foi publicada por Richard M. Dudley em 1967. A necessidade foi provada por Michael B. Marcus e Lawrence Shepp em 1970.

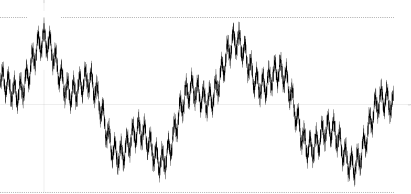
Existem exemplos de processos contínuos que violam a condição. Um exemplo encontrado por Marcus e Shepp é uma série aleatória de Fourier lacunar ${\ displaystyle X}$ ${\ displaystyle I (\ sigma) = \ infty;}$ ${\ displaystyle (*).}$

{\ displaystyle X_ {t} = \ sum _ {n = 1} ^ {\ infty} c_ {n} (\ xi _ {n} \ cos \ lambda _ {n} t + \ eta _ {n} \ sin \ lambda _ {n} t),}

onde estão variáveis aleatórias independentes com distribuição normal padrão ; as frequências são uma sequência de crescimento rápido; e os coeficientes satisfazem. A última relação implica de onde quase certamente, o que garante convergência uniforme da série de Fourier quase certamente, e a continuidade da amostra de ${\ displaystyle \ xi _ {1}, \ eta _ {1}, \ xi _ {2}, \ eta _ {2}, \ dots}$ ${\ displaystyle 0 <\ lambda _ {1} <\ lambda _ {2} <\ dots}$ ${\ displaystyle c_ {n}> 0}$ ${\ displaystyle \ textstyle \ sum _ {n} c_ {n} <\ infty.}$ ${\ displaystyle \ textstyle \ mathbb {E} \ sum _ {n} c_ {n} (| \ xi _ {n} | + | \ eta _ {n} |) = \ sum _ {n} c_ {n} \ mathbb {E} (| \ xi _ {n} | + | \ eta _ {n} |) = {\ text {const}} \ cdot \ sum _ {n} c_ {n} <\ infty,}$ ${\ displaystyle \ sum _ {n} c_ {n} (| \ xi _ {n} | + | \ eta _ {n} |) <\ infty}$ ${\ displaystyle X.}$

Autocorrelação de uma série lacunária de Fourier aleatória

Sua função de autocovariação

{\ displaystyle \ mathbb {E} X_ {t} X_ {t + h} = \ sum _ {n = 1} ^ {\ infty} c_ {n} ^ {2} \ cos \ lambda _ {n} h}

em nenhum lugar é monótono (veja a imagem), bem como a função correspondente ${\ displaystyle \ sigma,}$

{\ displaystyle \ sigma (h) = {\ sqrt {2 \ mathbb {E} X_ {t} X_ {t} -2 \ mathbb {E} X_ {t} X_ {t + h}}} = 2 {\ sqrt {\ sum _ {n = 1} ^ {\ infty} c_ {n} ^ {2} \ sin ^ {2} {\ frac {\ lambda _ {n} h} {2}}}}.}

Movimento browniano como parte integrante dos processos gaussianos

Um processo de Wiener (também conhecido como movimento browniano) é a integral de um processo gaussiano generalizado de ruído branco . Não é estacionário , mas tem incrementos estacionários.

O processo Ornstein-Uhlenbeck é um processo gaussiano estacionário .

A ponte browniana é (como o processo Ornstein-Uhlenbeck) um exemplo de um processo gaussiano cujos incrementos não são independentes .

O movimento browniano fracionário é um processo gaussiano cuja função de covariância é uma generalização daquela do processo de Wiener.

Lei zero-um de Driscoll

A lei zero-um de Driscoll é um resultado que caracteriza as funções de amostra geradas por um processo gaussiano.

Seja um processo gaussiano de média zero com função de covariância definida não negativa . Let Ser um Espaço de Hilbert do kernel Reproduzindo com kernel definido positivo . ${\ displaystyle f}$ ${\ displaystyle \ left \ {X_ {t}; t \ in T \ right \}}$ ${\ displaystyle K}$ ${\ displaystyle {\ mathcal {H}} (R)}$ ${\ displaystyle R}$

Então

{\ displaystyle \ lim _ {n \ to \ infty} \ operatorname {tr} [K_ {n} R_ {n} ^ {- 1}] <\ infty}

,

onde e são as matrizes de covariância de todos os pares possíveis de pontos, implica ${\ displaystyle K_ {n}}$ ${\ displaystyle R_ {n}}$ ${\ displaystyle n}$

{\ displaystyle \ Pr [f \ in {\ mathcal {H}} (R)] = 1}

.

O que mais,

{\ displaystyle \ lim _ {n \ to \ infty} \ operatorname {tr} [K_ {n} R_ {n} ^ {- 1}] = \ infty}

implica

{\ displaystyle \ Pr [f \ in {\ mathcal {H}} (R)] = 0}

.

Isso tem implicações significativas quando , como ${\ displaystyle K = R}$

{\ displaystyle \ lim _ {n \ to \ infty} \ operatorname {tr} [R_ {n} R_ {n} ^ {- 1}] = \ lim _ {n \ to \ infty} \ operatorname {tr} [ I] = \ lim _ {n \ to \ infty} n = \ infty}

.

Como tal, quase todos os caminhos de amostra de um processo gaussiano de média zero com kernel definido positivo estarão fora do espaço de Hilbert . ${\ displaystyle K}$ ${\ displaystyle {\ mathcal {H}} (K)}$

Processos gaussianos linearmente restritos

Para muitas aplicações de interesse, algum conhecimento pré-existente sobre o sistema em questão já é fornecido. Considere, por exemplo, o caso em que a saída do processo gaussiano corresponde a um campo magnético; aqui, o campo magnético real é limitado pelas equações de Maxwell e uma maneira de incorporar essa restrição ao formalismo do processo gaussiano seria desejável, pois isso provavelmente aumentaria a precisão do algoritmo.

Já existe um método sobre como incorporar restrições lineares em processos gaussianos:

Considere a função de saída (com valor vetorial) que é conhecida por obedecer à restrição linear (ou seja, é um operador linear) ${\ displaystyle f (x)}$ ${\ displaystyle {\ mathcal {F}} _ {X}}$

{\ displaystyle {\ mathcal {F}} _ {X} (f (x)) = 0.}

Em seguida, a restrição pode ser cumprida escolhendo onde é modelado como um processo gaussiano e encontrando st ${\ displaystyle {\ mathcal {F}} _ {X}}$ ${\ displaystyle f (x) = {\ mathcal {G}} _ {X} (g (x))}$ ${\ displaystyle g (x) \ sim {\ mathcal {GP}} (\ mu _ {g}, K_ {g})}$ ${\ displaystyle {\ mathcal {G}} _ {X}}$

{\ displaystyle {\ mathcal {F}} _ {X} ({\ mathcal {G}} _ {X} (g)) = 0 \ qquad \ forall g.}

Dado e usando o fato de que os processos gaussianos são fechados sob transformações lineares, o processo gaussiano para obedecer à restrição torna-se ${\ displaystyle {\ mathcal {G}} _ {X}}$ ${\ displaystyle f}$ ${\ displaystyle {\ mathcal {F}} _ {X}}$

{\ displaystyle f (x) = {\ mathcal {G}} _ {X} g \ sim {\ mathcal {GP}} ({\ mathcal {G}} _ {X} \ mu _ {g}, {\ mathcal {G}} _ {X} K_ {g} {\ mathcal {G}} _ {X '} ^ {T}).}

Portanto, as restrições lineares podem ser codificadas na função de média e covariância de um processo gaussiano.

Formulários

Um exemplo de regressão do processo gaussiano (previsão) em comparação com outros modelos de regressão.

Um processo gaussiano pode ser usado como uma distribuição de probabilidade a priori sobre funções na inferência bayesiana . Dado qualquer conjunto de N pontos no domínio desejado de suas funções, pegue um Gaussiano multivariado cujo parâmetro da matriz de covariância é a matriz de Gram de seus N pontos com algum kernel desejado e faça uma amostra desse Gaussiano. Para a solução do problema de predição de múltiplas saídas, foi desenvolvida a regressão do processo gaussiano para função com valor vetorial. Neste método, uma 'grande' covariância é construída, que descreve as correlações entre todas as variáveis de entrada e saída tomadas em N pontos no domínio desejado. Esta abordagem foi elaborada em detalhes para os processos gaussianos com valor de matriz e generalizada para processos com 'caudas mais pesadas' como processos de Student-t .

A inferência de valores contínuos com um processo gaussiano anterior é conhecida como regressão do processo gaussiano, ou krigagem ; estender a regressão do processo gaussiano a várias variáveis de destino é conhecido como cokriging . Os processos gaussianos são, portanto, úteis como uma ferramenta de interpolação multivariada não linear poderosa .

Os processos gaussianos também podem ser usados no contexto da mistura de modelos de especialistas, por exemplo. O fundamento lógico de tal estrutura de aprendizagem consiste na suposição de que um determinado mapeamento não pode ser bem capturado por um único modelo de processo gaussiano. Em vez disso, o espaço de observação é dividido em subconjuntos, cada um dos quais é caracterizado por uma função de mapeamento diferente; cada um deles é aprendido por meio de um componente de processo gaussiano diferente na mistura postulada.

Previsão de processo gaussiano, ou Krigagem

Regressão Gaussiana do Processo (predição) com kernel exponencial ao quadrado. O gráfico à esquerda é extraído da distribuição de função anterior. No meio são desenhados a partir da parte posterior. À direita está a previsão média com um desvio padrão sombreado.

Quando se trata de um problema de regressão de processo gaussiano geral (Krigagem), assume-se que para um processo gaussiano observado em coordenadas , o vetor de valores é apenas uma amostra de uma distribuição gaussiana multivariada de dimensão igual ao número de coordenadas observadas . Portanto, assumindo uma distribuição de média zero,, onde é a matriz de covariância entre todos os pares possíveis para um determinado conjunto de hiperparâmetros θ . Como tal, a probabilidade marginal logarítmica é: ${\ displaystyle f}$ ${\ displaystyle x}$ ${\ displaystyle f (x)}$ ${\ displaystyle n}$ ${\ displaystyle f (x ') \ sim N (0, K (\ theta, x, x'))}$ ${\ displaystyle K (\ theta, x, x ')}$ ${\ displaystyle (x, x ')}$

{\ displaystyle \ log p (f (x ') \ mid \ theta, x) = - {\ frac {1} {2}} f (x) ^ {T} K (\ theta, x, x') ^ {-1} f (x ') - {\ frac {1} {2}} \ log \ det (K (\ theta, x, x')) - {\ frac {n} {2}} \ log 2 \ pi}

e maximizar essa verossimilhança marginal em direção a θ fornece a especificação completa do processo gaussiano f . Pode-se notar brevemente neste ponto que o primeiro termo corresponde a um termo de penalidade para o não ajuste de um modelo aos valores observados e o segundo termo a um termo de penalidade que aumenta proporcionalmente à complexidade do modelo. Tendo especificado θ , fazer previsões sobre valores não observados nas coordenadas x * é então apenas uma questão de extrair amostras da distribuição preditiva onde a estimativa média posterior A é definida como ${\ displaystyle f (x ^ {*})}$ ${\ displaystyle p (y ^ {*} \ mid x ^ {*}, f (x), x) = N (y ^ {*} \ mid A, B)}$

{\ displaystyle A = K (\ theta, x ^ {*}, x) K (\ theta, x, x ') ^ {- 1} f (x)}

e a estimativa de variância posterior B é definida como:

{\ displaystyle B = K (\ theta, x ^ {*}, x ^ {*}) - K (\ theta, x ^ {*}, x) K (\ theta, x, x ') ^ {- 1 } K (\ theta, x ^ {*}, x) ^ {T}}

onde é a covariância entre a nova coordenada de estimativa x * e todas as outras coordenadas observadas x para um dado vetor de hiperparâmetro θ , e são definidas como antes e é a variância no ponto x * conforme ditado por θ . É importante notar que praticamente a estimativa média posterior (a "estimativa pontual") é apenas uma combinação linear das observações ; de maneira semelhante, a variância de é realmente independente das observações . Um conhecido gargalo na previsão do processo gaussiano é que a complexidade computacional da inferência e da avaliação da verossimilhança é cúbica no número de pontos | x | e, como tal, pode se tornar inviável para conjuntos de dados maiores. Trabalhos em processos gaussianos esparsos, que geralmente se baseiam na ideia de construir um conjunto representativo para um determinado processo f , procuram contornar esse problema. O método de krigagem pode ser usado no nível latente de um modelo não linear de efeitos mistos para uma previsão funcional espacial: esta técnica é chamada de krigagem latente. ${\ displaystyle K (\ theta, x ^ {*}, x)}$ ${\ displaystyle K (\ theta, x, x ')}$ ${\ displaystyle f (x)}$ ${\ displaystyle K (\ theta, x ^ {*}, x ^ {*})}$ ${\ displaystyle f (x ^ {*})}$ ${\ displaystyle f (x)}$ ${\ displaystyle f (x ^ {*})}$ ${\ displaystyle f (x)}$

Redes neurais bayesianas como processos gaussianos

As redes neurais bayesianas são um tipo particular de rede bayesiana que resulta do tratamento probabilístico de modelos de redes neurais artificiais e de aprendizagem profunda e da atribuição de uma distribuição prévia aos seus parâmetros . A computação em redes neurais artificiais é geralmente organizada em camadas sequenciais de neurônios artificiais . O número de neurônios em uma camada é chamado de largura da camada. À medida que a largura da camada aumenta, muitas redes neurais bayesianas se reduzem a um processo gaussiano com um kernel composicional de forma fechada . Este processo gaussiano é denominado Processo Gaussiano da Rede Neural (NNGP). Ele permite que as previsões das redes neurais bayesianas sejam avaliadas com mais eficiência e fornece uma ferramenta analítica para entender os modelos de aprendizado profundo .

Questões computacionais

Em aplicações práticas, os modelos de processos gaussianos são frequentemente avaliados em uma grade levando a distribuições normais multivariadas. O uso desses modelos para predição ou estimativa de parâmetro usando máxima verossimilhança requer a avaliação de uma densidade gaussiana multivariada, que envolve o cálculo do determinante e do inverso da matriz de covariância. Ambas as operações têm complexidade computacional cúbica, o que significa que mesmo para grades de tamanhos modestos, ambas as operações podem ter um custo computacional proibitivo. Essa desvantagem levou ao desenvolvimento de métodos de aproximação múltipla .

Veja também

Referências

links externos

Programas

GPML: Uma abrangente caixa de ferramentas Matlab para regressão e classificação GP
STK: uma caixa de ferramentas pequena (Matlab / Octave) para modelagem de Krigagem e GP
Módulo Kriging no framework UQLab (Matlab)
Função Matlab / Octave para campos gaussianos estacionários
Yelp MOE - Um mecanismo de otimização de caixa preta usando aprendizagem de processo Gaussiano
ooDACE - Uma caixa de ferramentas do Matlab Kriging orientada a objetos flexível.
GPstuff - caixa de ferramentas de processo gaussiano para Matlab e Octave
GPy - Uma estrutura de processos gaussianos em Python
GSTools - Uma caixa de ferramentas geoestatística, incluindo regressão do processo Gaussiano, escrita em Python
Demonstração de regressão de processo Gaussiano interativo
Biblioteca básica de processos gaussianos escrita em C ++ 11
scikit-learn - Uma biblioteca de aprendizado de máquina para Python que inclui regressão e classificação de processo Gaussiano
[1] - O Kriging toolKit (KriKit) é desenvolvido no Institute of Bio- and Geosciences 1 (IBG-1) de Forschungszentrum Jülich (FZJ)

Languages

In other projects