Categoria monoidal - Monoidal category

Em matemática , uma categoria monoidal (ou categoria tensorial ) é uma categoria equipada com um bifunctor${\ displaystyle \ mathbf {C}}$

${\ displaystyle \ otimes: \ mathbf {C} \ times \ mathbf {C} \ to \ mathbf {C}}$

que é associativo até um isomorfismo natural , e um objeto I que é uma identidade esquerda e direita para ⊗, novamente até um isomorfismo natural. Os isomorfismos naturais associados estão sujeitos a certas condições de coerência , que garantem que todos os diagramas relevantes comutam .

O ordinária produto tensor faz espaços vetoriais , grupos abelianos , R -modules , ou R -álgebras em categorias monoidais. As categorias monoidais podem ser vistas como uma generalização desses e de outros exemplos. Cada ( pequena ) categoria monoidal também pode ser vista como uma " categorização " de um monóide subjacente , a saber, o monóide cujos elementos são as classes de isomorfismo dos objetos da categoria e cuja operação binária é dada pelo produto tensorial da categoria.

Uma aplicação bastante diferente, da qual categorias monoidais podem ser consideradas uma abstração, é a de um sistema de tipos de dados fechado sob um construtor de tipo que pega dois tipos e constrói um tipo agregado; os tipos são os objetos e é o construtor agregado. A associatividade até o isomorfismo é, então, uma forma de expressar que diferentes maneiras de agregar os mesmos dados - como e - armazenam as mesmas informações, embora os valores agregados não precisem ser os mesmos. O tipo de agregado pode ser análogo à operação de adição (tipo de soma) ou de multiplicação (tipo de produto). Para o produto tipo, o objeto de identidade é a unidade , portanto, há apenas um habitante do tipo, e é por isso que um produto com ele é sempre isomórfico ao outro operando. Para o tipo soma, o objeto identidade é o tipo vazio , que não armazena nenhuma informação e é impossível se dirigir a um habitante. O conceito de categoria monoidal não presume que os valores de tais tipos agregados podem ser desmontados; pelo contrário, fornece uma estrutura que unifica a teoria da informação clássica e quântica . ${\ displaystyle \ otimes}$${\ displaystyle ((a, b), c)}$${\ displaystyle (a, (b, c))}$${\ displaystyle ()}$

Na teoria das categorias , as categorias monoidais podem ser usadas para definir o conceito de um objeto monoidal e uma ação associada nos objetos da categoria. Eles também são usados ​​na definição de uma categoria enriquecida .

As categorias monoidais têm inúmeras aplicações fora da teoria das categorias propriamente dita. Eles são usados ​​para definir modelos para o fragmento multiplicativo da lógica linear intuicionista . Eles também formam a base matemática para a ordem topológica na física da matéria condensada . Trançados categorias monoidais têm aplicações em informação quântica , teoria quântica de campos , e a teoria das cordas .

Definição formal

Uma categoria monoidal é uma categoria equipada com uma estrutura monoidal. Uma estrutura monoidal consiste no seguinte: ${\ displaystyle \ mathbf {C}}$

• um bifunctor chamado produto tensor ou produto monoidal ,${\ displaystyle \ otimes \ colon \ mathbf {C} \ times \ mathbf {C} \ to \ mathbf {C}}$
• um objeto chamado de objeto de unidade ou objeto de identidade ,${\ displaystyle I}$
• três isomorfismos naturais sujeitos a certas condições de coerência expressando o fato de que a operação tensorial
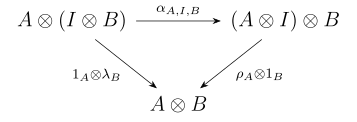
  • é associativo: há uma forma natural (em cada um dos três argumentos , , ) isomorfismo , chamado associativa , com componentes ,${\ displaystyle A}$${\ displaystyle B}$${\ displaystyle C}$${\ displaystyle \ alpha}$${\ displaystyle \ alpha _ {A, B, C} \ colon A \ otimes (B \ otimes C) \ cong (A \ otimes B) \ otimes C}$
  • tem como identidade esquerda e direita: existem dois isomorfismos naturais e , respectivamente chamados de unitor esquerdo e direito , com os componentes e .${\ displaystyle I}$${\ displaystyle \ lambda}$${\ displaystyle \ rho}$${\ displaystyle \ lambda _ {A} \ dois pontos I \ otimes A \ cong A}$${\ displaystyle \ rho _ {A} \ dois pontos A \ otimes I \ cong A}$

Observe que uma boa maneira de lembrar como e agir é por aliteração; Lambda , , cancela a identidade na esquerda , enquanto Rho , , cancela a identidade na direita . ${\ displaystyle \ lambda}$${\ displaystyle \ rho}$${\ displaystyle \ lambda}$${\ displaystyle \ rho}$

As condições de coerência para essas transformações naturais são:

• para todos , , e em , o pentágono diagrama${\ displaystyle A}$${\ displaystyle B}$${\ displaystyle C}$${\ displaystyle D}$${\ displaystyle \ mathbf {C}}$

comuta ;

• para todos e em , o diagrama do triângulo${\ displaystyle A}$${\ displaystyle B}$${\ displaystyle \ mathbf {C}}$

comuta.

Uma categoria monoidal estrita é aquela para a qual os isomorfismos naturais α , λ e ρ são identidades. Cada categoria monoidal é monoidalmente equivalente a uma categoria monoidal estrita.

Exemplos

• Qualquer categoria com produtos finitos pode ser considerada monoidal, com o produto como o produto monoidal e o objeto terminal como a unidade. Essa categoria é às vezes chamada de categoria monoidal cartesiana . Por exemplo:
  • Conjunto , a categoria de conjuntos com o produto cartesiano, qualquer conjunto de um elemento particular servindo como unidade.
  • Cat , a categoria de pequenas categorias com a categoria de produto , onde a categoria com um objeto e apenas seu mapa de identidade é a unidade.
• Dualmente, qualquer categoria com coprodutos finitos é monoidal, com o coproduto como o produto monoidal e o objeto inicial como a unidade. Essa categoria monoidal é chamada monoidal cocartesiana
• R -Mod , a categoria de módulos sobre um anel comutativo R , é uma categoria monoidal com o produto tensorial dos módulos ⊗ _R servindo como o produto monoidal e o anel R (pensado como um módulo sobre si mesmo) servindo como a unidade. Como casos especiais, temos:
  • K -Vect , a categoria de espaços vetoriais sobre um campo K , com o espaço vetorial unidimensional K servindo como unidade.
  • Ab , a categoria dos grupos abelianos , com o grupo de inteiros Z servindo como unidade.
• Para qualquer anel conmutativo R , a categoria de R -álgebras é monoidal com o produto tensor de álgebra de como o produto e R como a unidade.
• A categoria de espaços pontiagudos (restrito a espaços gerados compactamente, por exemplo) é monoidal com o produto esmagado servindo como o produto e a esfera 0 pontiaguda (um espaço discreto de dois pontos) servindo como a unidade.
• A categoria de todos os endofunctors em uma categoria C é uma categoria monoidal estrita com a composição de functores como o produto e o functor de identidade como a unidade.
• Assim como para qualquer categoria E , a subcategoria completa abrangida por qualquer dado objeto é um monóide, é o caso de qualquer 2-categoria E , e qualquer objeto C em Ob ( E ), a 2-subcategoria completa de E abrangida por { C } é uma categoria monoidal. No caso E = Cat , temos o exemplo de endofunctors acima.
• As semilattices de encontro delimitadas acima são categorias monoidais simétricas estritas : o produto é justo e a identidade é o elemento superior.
• Qualquer monóide comum é uma pequena categoria monoidal com conjunto de objetos , apenas identidades para morfismos , como tensorproduto e como seu objeto de identidade. Por outro lado, o conjunto de classes de isomorfismo (se tal coisa faz sentido) de uma categoria monoidal é um monóide do produto tensorial.${\ displaystyle (M, \ cdot, 1)}$${\ displaystyle M}$${\ displaystyle \ cdot}$${\ displaystyle 1}$

Pré-encomendas monoidais

As pré-encomendas monoidais, também conhecidas como "monóides pré-encomendadas", são casos especiais de categorias monoidais. Esse tipo de estrutura surge na teoria dos sistemas de reescrita de cordas , mas também é abundante na matemática pura. Por exemplo, o conjunto de números naturais tem uma estrutura monoidal (usando + e 0) e uma estrutura de pré - ordem (usando ≤), que juntas formam uma pré-ordem monoidal, basicamente porque e implica . Agora apresentamos o caso geral. ${\ displaystyle \ mathbb {N}}$${\ displaystyle m \ leq n}$${\ displaystyle m '\ leq n'}$${\ displaystyle m + m '\ leq n + n'}$

É sabido que uma pré-venda pode ser considerado como uma categoria C , de tal forma que para cada dois objetos , existe no máximo um morfismo em C . Se acontecer de haver um morfismo de c para c ' , poderíamos escrever , mas na seção atual achamos mais conveniente expressar esse fato em forma de seta . Como existe no máximo um desses morfismos, nunca precisamos dar a ele um nome, como . Os reflexividade e transitividade propriedades de um pedido são, respectivamente, responsável por pelo morfismo identidade e a fórmula da composição em C . Nós escrevemos sse e , ou seja, se eles são isomorfos em C . Observe que, em uma ordem parcial , quaisquer dois objetos isomórficos são de fato iguais. ${\ displaystyle c, c '\ in \ mathrm {Ob} (\ mathbf {C})}$${\ displaystyle c \ a c '}$${\ displaystyle c \ leq c '}$${\ displaystyle c \ a c '}$${\ displaystyle f \ colon c \ to c '}$${\ displaystyle c \ cong c '}$${\ displaystyle c \ leq c '}$${\ displaystyle c '\ leq c}$

Avançando, suponha que deseja adicionar uma estrutura monoidal à pré-venda C . Para fazer isso, devemos escolher

• um objeto , chamado de unidade monoidal , e${\ displaystyle I \ in \ mathbf {C}}$
• um functor , que denotaremos simplesmente pelo ponto " ", chamado de multiplicação monoidal .${\ displaystyle \ mathbf {C} \ times \ mathbf {C} \ to \ mathbf {C}}$${\ displaystyle \; \ cdot \;}$

Portanto, para quaisquer dois objetos , temos um objeto . Devemos escolher e ser associativos e unitais, até o isomorfismo. Isso significa que devemos ter: ${\ displaystyle c_ {1}, c_ {2}}$${\ displaystyle c_ {1} \ cdot c_ {2}}$${\ displaystyle I}$${\ displaystyle \ cdot}$

${\ displaystyle (c_ {1} \ cdot c_ {2}) \ cdot c_ {3} \ cong c_ {1} \ cdot (c_ {2} \ cdot c_ {3})}$e .${\ displaystyle I \ cdot c \ cong c \ cong c \ cdot I}$

Além disso, o fato de que · é necessário para ser um functor significa - no presente caso, onde C é uma pré-encomenda - nada mais do que o seguinte:

se e então .${\ displaystyle c_ {1} \ a c_ {1} '}$${\ displaystyle c_ {2} \ a c_ {2} '}$${\ displaystyle (c_ {1} \ cdot c_ {2}) \ to (c_ {1} '\ cdot c_ {2}')}$

As condições adicionais de coerência para categorias monoidais são vazias neste caso porque cada diagrama comuta em uma pré-encomenda.

Observe que se C for uma ordem parcial, a descrição acima é simplificada ainda mais, porque os isomorfismos de associatividade e unitalidade tornam-se igualidades. Outra simplificação ocorre se assumirmos que o conjunto de objetos é o monóide livre em um conjunto gerador . Neste caso, poderíamos escrever , onde * denota a estrela de Kleene e a unidade monoidal I representa a string vazia. Se começarmos com um conjunto R de morfismos geradores (fatos sobre ≤), recuperamos a noção usual de sistema semi-Thue , onde R é chamado de "regra de reescrita". ${\ displaystyle \ Sigma}$${\ displaystyle \ mathrm {Ob} (\ mathbf {C}) = \ Sigma ^ {*}}$

Para retornar ao nosso exemplo, seja N a categoria cujos objetos são os números naturais 0, 1, 2, ..., com um único morfismo se estiver na ordem usual (e sem morfismos de i a j caso contrário), e um morfismo monoidal estrutura com a unidade monoidal dada por 0 e a multiplicação monoidal dada pela adição usual ,. Então N é uma pré-ordem monoidal; na verdade, é aquele gerado livremente por um único objeto 1, e um único morfismo 0 ≤ 1, onde novamente 0 é a unidade monoidal. ${\ displaystyle i \ a j}$${\ displaystyle i \ leq j}$${\ displaystyle i \ cdot j: = i + j}$

Propriedades e noções associadas

Resulta das três que determinam as condições de coerência que uma grande classe de diagramas (ou seja, cujo diagramas morphisms são construídos utilizando , , , identidades e produto tensor) comute: este é Mac Lane " coerência teorema ". Às vezes é afirmado incorretamente que todos esses diagramas comutam. ${\ displaystyle \ alpha}$${\ displaystyle \ lambda}$${\ displaystyle \ rho}$

Há uma noção geral de objeto monóide em uma categoria monoidal, que generaliza a noção comum de monóide da álgebra abstrata . Monóides comuns são precisamente os objetos monoidais na categoria monoidal cartesiana Conjunto . Além disso, qualquer (pequena) categoria monoidal estrita pode ser vista como um objeto monoidal na categoria de categorias Cat (equipado com a estrutura monoidal induzida pelo produto cartesiano).

Os functores monoidais são os functores entre as categorias monoidais que preservam o produto tensorial e as transformações naturais monoidais são as transformações naturais, entre esses functores, que são "compatíveis" com o produto tensorial.

Cada categoria monoidal pode ser vista como a categoria B (∗, ∗) de uma bicategoria B com apenas um objeto, denotado ∗.

O conceito de uma categoria C enriquecido em uma categoria monoidal H substitui a noção de um conjunto de morphisms entre pares de objectos em C com a noção de um H -object de morphisms entre cada dois objectos em C .

Categoria monoidal estrita gratuita

Para cada categoria C , a categoria monoidal estrita livre Σ ( C ) pode ser construída da seguinte forma:

• seus objetos são listas (sequências finitas) A ₁ , ..., A _n de objetos de C ;
• existem setas entre dois objetos A ₁ , ..., A _m e B ₁ , ..., B _n apenas se m = n , e então as setas são listas (sequências finitas) de setas f ₁ : A ₁ → B ₁ , ..., f _n : A _n → B _n de C ;
• o produto tensorial de dois objetos A ₁ , ..., A _n e B ₁ , ..., B _m é a concatenação A ₁ , ..., A _n , B ₁ , ..., B _m dos dois listas e, da mesma forma, o produto tensorial de dois morfismos é dado pela concatenação de listas. O objeto de identidade é a lista vazia.

Esta operação Σ mapeando a categoria C para Σ ( C ) pode ser estendida para uma 2- mônada estrita no Cat .

Especializações

• Se, em uma categoria monoidal, e são naturalmente isomórficos de maneira compatível com as condições de coerência, falamos de uma categoria monoidal trançada . Se, além disso, esse isomorfismo natural é seu próprio inverso, temos uma categoria monoidal simétrica .${\ displaystyle A \ otimes B}$${\ displaystyle B \ otimes A}$
• Uma categoria monoidal fechada é uma categoria monoidal onde o functor tem um adjunto à direita , que é chamado de "Hom-functor interno" . Os exemplos incluem categorias fechadas cartesianas , como Set , a categoria de conjuntos, e categorias fechadas compactas , como FdVect , a categoria de espaços vetoriais de dimensão finita.${\ displaystyle X \ mapsto X \ otimes A}$${\ displaystyle X \ mapsto \ mathrm {Hom} _ {\ mathbf {C}} (A, X)}$
• Categorias autónomos (ou compacto categorias fechadas ou categorias rígidas ) são categorias monoidais em que existem duos com propriedades agradáveis; eles abstraem a ideia do FdVect .
• Categorias adaga simétricas monoidais , equipadas com um functor adaga extra, abstraindo a ideia de FdHilb , espaços de Hilbert de dimensão finita. Isso inclui as categorias compactas de punhal .
• As categorias de Tannakian são categorias monoidais enriquecidas sobre um campo, que são muito semelhantes às categorias de representação de grupos algébricos lineares .

Veja também

• Esqueleto (teoria da categoria)
• Categoria esférica
• Ação de categoria monoidal

Referências

• Joyal, André ; Street, Ross (1993). "Categorias de tensores trançados". Advances in Mathematics 102 , 20-78.
• Joyal, André ; Street, Ross (1988). " Diagramas planares e álgebra tensorial ".
• Kelly, G. Max (1964). "Sobre as Condições de MacLane para Coerência de Associatividades Naturais, Comutatividades, etc." Journal of Algebra 1 , 397-402
• Kelly, G. Max (1982). Conceitos básicos da teoria das categorias enriquecidas (PDF) . Série de notas de aula da London Mathematical Society No. 64. Cambridge University Press.
• Mac Lane, Saunders (1963). "Associatividade Natural e Comutatividade". Rice University Studies 49 , 28-46.
• Mac Lane, Saunders (1998), Categories for the Working Mathematician (2ª ed.). Nova York: Springer-Verlag.
• Categoria monoidal em nLab

links externos

• Mídia relacionada à categoria Monoidal no Wikimedia Commons