Círculo de Spieker - Spieker circle
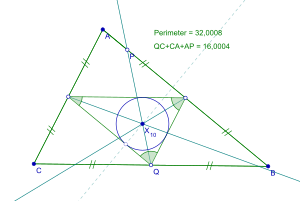
Em geometria , o incircle do triângulo medial de um triângulo é o círculo de Spieker , em homenagem ao geômetra alemão do século 19 Theodor Spieker . Seu centro, o centro de Spieker , além de ser o incentivo do triângulo medial, é o centro de massa da fronteira de densidade uniforme do triângulo. O centro de Spieker é também o ponto onde todos os três cutelos do triângulo (bissetores de perímetro com uma extremidade no ponto médio de um lado) se cruzam.
História
O círculo e o centro Spieker receberam o nome de Theodor Spieker , um matemático e professor de Potsdam, Alemanha. Em 1862, ele publicou Lehrbuch der ebenen geometrie mit übungsaufgaben für höhere lehranstalten , que trata da geometria plana. Devido a esta publicação, influente na vida de muitos cientistas e matemáticos famosos, incluindo Albert Einstein , Spieker se tornou o matemático que deu nome ao círculo e centro de Spieker.
Construção
Para encontrar o círculo Spieker de um triângulo, o triângulo medial deve primeiro ser construído a partir dos pontos médios de cada lado do triângulo original. O círculo é então construído de forma que cada lado do triângulo medial seja tangente ao círculo dentro do triângulo medial, criando o incircle . Este centro do círculo é denominado centro Spieker.
Pontos e linhas de Nagel
Os círculos de Spieker também têm relações com os pontos Nagel . O incentivo do triângulo e o ponto de Nagel formam uma linha dentro do círculo de Spieker. O meio deste segmento de linha é o centro de Spieker. A linha de Nagel é formada pelo incentivo do triângulo, o ponto de Nagel e o centróide do triângulo. O centro de Spieker sempre estará nesta linha.
Círculo de nove pontos e linha de Euler
Os círculos de Spieker foram inicialmente considerados muito semelhantes aos círculos de nove pontos de Julian Coolidge. Neste momento, ele ainda não foi identificado como o círculo Spieker, mas é referido como o "círculo P" em todo o livro. O círculo de nove pontos com a linha de Euler e o círculo de Spieker com a linha de Nagel são análogos um ao outro, mas não são duais , tendo apenas semelhanças duais. Uma semelhança entre o círculo de nove pontos e o círculo de Spieker trata de sua construção. O círculo de nove pontos é o círculo circunscrito do triângulo medial, enquanto o círculo de Spieker é o círculo inscrito do triângulo medial. Em relação às suas linhas associadas, o incentivo para a linha Nagel refere-se ao circuncentro para a linha Euler. Outro ponto análogo é o ponto de Nagel e o otocentro , com o ponto de Nagel associado ao círculo de Spieker e o ortocentro associado ao círculo de nove pontos. Cada círculo encontra os lados do triângulo medial onde as linhas do ortocentro, ou o ponto de Nagel, aos vértices do triângulo original encontram os lados do triângulo medial.
Spieker cônica
O círculo de nove pontos com a linha de Euler foi generalizado na cônica de nove pontos. Por meio de um processo semelhante, devido às propriedades análogas dos dois círculos, o círculo de Spieker também foi capaz de ser generalizado na cônica de Spieker. A cônica de Spieker ainda é encontrada dentro do triângulo medial e toca cada lado do triângulo medial, porém não encontra esses lados do triângulo nos mesmos pontos. Se as linhas são construídas de cada vértice do triângulo medial até o ponto de Nagel, então o ponto médio de cada uma dessas linhas pode ser encontrado. Além disso, os pontos médios de cada lado do triângulo medial são encontrados e conectados ao ponto médio da linha oposta através do ponto Nagel. Cada uma dessas linhas compartilha um ponto médio comum, S. Com cada uma dessas linhas refletidas por S, o resultado é 6 pontos dentro do triângulo medial. Desenhe uma cônica através de qualquer um desses 5 pontos refletidos e a cônica tocará o ponto final. Isso foi comprovado por de Villiers em 2006.
Círculo radical de Spieker
O círculo radical de Spieker é o círculo, centralizado no centro de Spieker, que é ortogonal aos três círculos do triângulo medial.
Referências
- Johnson, Roger A. (1929). Geometria moderna . Boston: Houghton Mifflin. Reimpressão de Dover, 1960.
- Kimberling, Clark (1998). "Centros de triângulos e triângulos centrais". Congressus Numerantium . 129 : i – xxv, 1–295.
links externos
- Spieker Conic e generalização da linha de Nagel em Dynamic Geometry Sketches Generaliza o círculo de Spieker e a linha de Nagel associada.
