Hierarquia aritmética - Arithmetical hierarchy

Uma ilustração de como os níveis da hierarquia interagem e onde algumas categorias de conjuntos básicos se encontram dentro dela.

Na lógica matemática , a hierarquia aritmética , hierarquia aritmética ou hierarquia Kleene – Mostowski ( em homenagem aos matemáticos Stephen Cole Kleene e Andrzej Mostowski ) classifica certos conjuntos com base na complexidade das fórmulas que os definem. Qualquer conjunto que recebe uma classificação é denominado aritmético .

A hierarquia aritmética é importante na teoria da recursão , na teoria dos conjuntos descritivos eficazes e no estudo de teorias formais como a aritmética de Peano .

O algoritmo Tarski – Kuratowski fornece uma maneira fácil de obter um limite superior nas classificações atribuídas a uma fórmula e ao conjunto que ela define.

A hierarquia hiperaritmética e a hierarquia analítica estendem a hierarquia aritmética para classificar fórmulas e conjuntos adicionais.

A hierarquia aritmética das fórmulas

A hierarquia aritmética atribui classificações às fórmulas na linguagem da aritmética de primeira ordem . As classificações são denotadas e para números naturais n (incluindo 0). As letras gregas aqui são símbolos de face clara , o que indica que as fórmulas não contêm parâmetros definidos. ${\ displaystyle \ Sigma _ {n} ^ {0}}$${\ displaystyle \ Pi _ {n} ^ {0}}$

Se uma fórmula é logicamente equivalente a uma fórmula com apenas quantificadores limitados , são atribuídas as classificações e . ${\ displaystyle \ phi}$${\ displaystyle \ phi}$${\ displaystyle \ Sigma _ {0} ^ {0}}$${\ displaystyle \ Pi _ {0} ^ {0}}$

As classificações e são definidas indutivamente para cada número natural n usando as seguintes regras: ${\ displaystyle \ Sigma _ {n} ^ {0}}$${\ displaystyle \ Pi _ {n} ^ {0}}$

• Se for logicamente equivalente a uma fórmula do formulário , onde está , então é atribuída a classificação .${\ displaystyle \ phi}$${\ displaystyle \ existe m_ {1} \ existe m_ {2} \ cdots \ existe m_ {k} \ psi}$${\ displaystyle \ psi}$${\ displaystyle \ Pi _ {n} ^ {0}}$${\ displaystyle \ phi}$${\ displaystyle \ Sigma _ {n + 1} ^ {0}}$
• Se for logicamente equivalente a uma fórmula do formulário , onde está , então é atribuída a classificação .${\ displaystyle \ phi}$${\ displaystyle \ forall m_ {1} \ forall m_ {2} \ cdots \ forall m_ {k} \ psi}$${\ displaystyle \ psi}$${\ displaystyle \ Sigma _ {n} ^ {0}}$${\ displaystyle \ phi}$${\ displaystyle \ Pi _ {n + 1} ^ {0}}$

Uma fórmula é equivalente a uma fórmula que começa com alguns quantificadores existenciais e alterna tempos entre séries de quantificadores existenciais e universais ; enquanto uma fórmula é equivalente a uma fórmula que começa com alguns quantificadores universais e alterna analogamente. ${\ displaystyle \ Sigma _ {n} ^ {0}}$${\ displaystyle n-1}$${\ displaystyle \ Pi _ {n} ^ {0}}$

Como toda fórmula de primeira ordem tem uma forma normal prenex , toda fórmula recebe pelo menos uma classificação. Porque quantificadores redundantes podem ser adicionados a qualquer fórmula, uma vez que uma fórmula seja atribuída à classificação ou ela será atribuída às classificações e para cada r> n . A única classificação relevante atribuída a uma fórmula é, portanto, aquela com o mínimo n ; todas as outras classificações podem ser determinadas a partir dele. ${\ displaystyle \ Sigma _ {n} ^ {0}}$${\ displaystyle \ Pi _ {n} ^ {0}}$${\ displaystyle \ Sigma _ {r} ^ {0}}$${\ displaystyle \ Pi _ {r} ^ {0}}$

A hierarquia aritmética de conjuntos de números naturais

Um conjunto X de números naturais é definido pela fórmula φ na linguagem da aritmética de Peano (a linguagem de primeira ordem com os símbolos "0" para zero, "S" para a função sucessora, "+" para adição, "×" para multiplicação , e "=" para igualdade), se os elementos de X forem exatamente os números que satisfazem φ. Ou seja, para todos os números naturais n ,

${\ displaystyle n \ in X \ Leftrightarrow \ mathbb {N} \ models \ varphi ({\ underline {n}}),}$

onde é o numeral na linguagem da aritmética correspondente a . Um conjunto é definível na aritmética de primeira ordem se for definido por alguma fórmula na linguagem da aritmética de Peano. ${\ displaystyle {\ underline {n}}}$${\ displaystyle n}$

Cada conjunto X de números naturais que é definível em aritmética de primeira ordem é atribuído classificações da forma , e , em que é um número natural, como se segue. Se X é definível por uma fórmula, então X é atribuída a classificação . Se X é definível por uma fórmula, então X é atribuída a classificação . Se X for ambos, e então será atribuída a classificação adicional . ${\ displaystyle \ Sigma _ {n} ^ {0}}$${\ displaystyle \ Pi _ {n} ^ {0}}$${\ displaystyle \ Delta _ {n} ^ {0}}$${\ displaystyle n}$${\ displaystyle \ Sigma _ {n} ^ {0}}$${\ displaystyle \ Sigma _ {n} ^ {0}}$${\ displaystyle \ Pi _ {n} ^ {0}}$${\ displaystyle \ Pi _ {n} ^ {0}}$${\ displaystyle \ Sigma _ {n} ^ {0}}$${\ displaystyle \ Pi _ {n} ^ {0}}$${\ displaystyle X}$${\ displaystyle \ Delta _ {n} ^ {0}}$

Observe que raramente faz sentido falar de fórmulas; o primeiro quantificador de uma fórmula é existencial ou universal. Portanto, um conjunto não é definido por uma fórmula; em vez disso, existem fórmulas e que definem o conjunto. Por exemplo, o conjunto de números naturais ímpares pode ser definido por ou . ${\ displaystyle \ Delta _ {n} ^ {0}}$${\ displaystyle \ Delta _ {n} ^ {0}}$${\ displaystyle \ Delta _ {n} ^ {0}}$${\ displaystyle \ Sigma _ {n} ^ {0}}$${\ displaystyle \ Pi _ {n} ^ {0}}$${\ displaystyle n}$${\ displaystyle \ forall k (n \ neq 2 \ times k)}$${\ displaystyle \ existe k (n = 2 \ vezes k + 1)}$

Uma definição paralela é usada para definir a hierarquia aritmética em poderes cartesianos finitos do conjunto de números naturais. Em vez de fórmulas com uma variável livre, fórmulas com k variáveis ​​de número livre são usadas para definir a hierarquia aritmética em conjuntos de k - tuplas de números naturais. Na verdade, eles estão relacionados pelo uso de uma função de emparelhamento .

Hierarquias aritméticas relativizadas

Assim como podemos definir o que significa para um conjunto X ser recursivo em relação a outro conjunto Y , permitindo que o cálculo que define X consulte Y como um oráculo, podemos estender essa noção a toda a hierarquia aritmética e definir o que significa para X ser ser , ou em Y , denotado respectivamente e . Para fazer isso, fixe um conjunto de inteiros Y e adicione um predicado para associação em Y à linguagem da aritmética de Peano. Dizemos então que X está dentro se for definido por uma fórmula nesta linguagem expandida. Em outras palavras, X é se ele é definido por uma fórmula autorizados a fazer perguntas sobre filiação em Y . Alternativamente, pode-se ver os conjuntos como aqueles conjuntos que podem ser construídos começando com conjuntos recursivos em Y e alternativamente tomando uniões e interseções desses conjuntos até n vezes. ${\ displaystyle \ Sigma _ {n} ^ {0}}$${\ displaystyle \ Delta _ {n} ^ {0}}$${\ displaystyle \ Pi _ {n} ^ {0}}$${\ displaystyle \ Sigma _ {n} ^ {0, Y}}$ ${\ displaystyle \ Delta _ {n} ^ {0, Y}}$${\ displaystyle \ Pi _ {n} ^ {0, Y}}$${\ displaystyle \ Sigma _ {n} ^ {0, Y}}$${\ displaystyle \ Sigma _ {n} ^ {0}}$${\ displaystyle \ Sigma _ {n} ^ {0, Y}}$${\ displaystyle \ Sigma _ {n} ^ {0}}$${\ displaystyle \ Sigma _ {n} ^ {0, Y}}$

Por exemplo, seja Y um conjunto de inteiros. Seja X o conjunto de números divisíveis por um elemento de Y. Então X é definido pela fórmula, então X está dentro ( na verdade também está dentro , pois poderíamos ligar ambos os quantificadores por n). ${\ displaystyle \ phi (n) = \ existe m \ existe t (Y (m) \ terra m \ vezes t = n)}$${\ displaystyle \ Sigma _ {1} ^ {0, Y}}$${\ displaystyle \ Delta _ {0} ^ {0, Y}}$

Redutibilidade aritmética e graus

A redutibilidade aritmética é uma noção intermediária entre a redutibilidade de Turing e a redutibilidade hiperaritmética .

Um conjunto é aritmético (também aritmético e aritmeticamente definível ) se for definido por alguma fórmula na linguagem da aritmética de Peano. Equivalentemente, X é aritmético se X for ou para algum inteiro n . Um conjunto X é aritmético em um conjunto Y , denotado , se X é definidos como alguns fórmula na língua de Peano aritmética estendido por um predicado para a adesão em Y . Equivalentemente, X é aritmético em Y se X estiver em ou para algum inteiro n . Um sinónimo para a é: X é aritmeticamente redutível para Y . ${\ displaystyle \ Sigma _ {n} ^ {0}}$${\ displaystyle \ Pi _ {n} ^ {0}}$ ${\ displaystyle X \ leq _ {A} Y}$${\ displaystyle \ Sigma _ {n} ^ {0, Y}}$${\ displaystyle \ Pi _ {n} ^ {0, Y}}$${\ displaystyle X \ leq _ {A} Y}$

A relação é reflexiva e transitiva e, portanto, a relação definida pela regra ${\ displaystyle X \ leq _ {A} Y}$${\ displaystyle \ equiv _ {A}}$

${\ displaystyle X \ equiv _ {A} Y \ Leftrightarrow X \ leq _ {A} Y \ land Y \ leq _ {A} X}$

é uma relação de equivalência. As classes de equivalência dessa relação são chamadas de graus aritméticos ; eles são parcialmente ordenados em . ${\ displaystyle \ leq _ {A}}$

A hierarquia aritmética de subconjuntos do espaço de Cantor e Baire

O espaço de Cantor , denotado , é o conjunto de todas as sequências infinitas de 0s e 1s; o espaço de Baire , denotado ou , é o conjunto de todas as sequências infinitas de números naturais. Observe que os elementos do espaço Cantor podem ser identificados com conjuntos de inteiros e elementos do espaço Baire com funções de inteiros a inteiros. ${\ displaystyle 2 ^ {\ omega}}$${\ displaystyle \ omega ^ {\ omega}}$${\ displaystyle {\ mathcal {N}}}$

A axiomatização comum da aritmética de segunda ordem usa uma linguagem baseada em conjuntos em que os quantificadores de conjuntos podem ser vistos naturalmente como quantificadores no espaço de Cantor. A classificação é atribuída a um subconjunto do espaço Cantor se for definível por uma fórmula. O conjunto recebe a classificação se for definível por uma fórmula. Se o conjunto é ao mesmo tempo e , em seguida, é dado a classificação adicional . Por exemplo, deixe ser o conjunto de todas as cadeias binárias infinitas que não são todas 0 (ou equivalentemente o conjunto de todos os conjuntos não vazios de inteiros). Como vemos, isso é definido por uma fórmula e, portanto, é um conjunto. ${\ displaystyle \ Sigma _ {n} ^ {0}}$${\ displaystyle \ Sigma _ {n} ^ {0}}$${\ displaystyle \ Pi _ {n} ^ {0}}$${\ displaystyle \ Pi _ {n} ^ {0}}$${\ displaystyle \ Sigma _ {n} ^ {0}}$${\ displaystyle \ Pi _ {n} ^ {0}}$${\ displaystyle \ Delta _ {n} ^ {0}}$${\ displaystyle O \ subset 2 ^ {\ omega}}$${\ displaystyle O = \ {X \ in 2 ^ {\ omega} | \ existe n (X (n) = 1) \}}$${\ displaystyle O}$${\ displaystyle \ Sigma _ {1} ^ {0}}$${\ displaystyle \ Sigma _ {1} ^ {0}}$

Observe que, embora os elementos do espaço Cantor (considerados como conjuntos de inteiros) e subconjuntos do espaço Cantor sejam classificados em hierarquias aritméticas, eles não são a mesma hierarquia. Na verdade, a relação entre as duas hierarquias é interessante e não trivial. Por exemplo, os elementos do espaço Cantor não são (em geral) iguais aos elementos do espaço Cantor, então este é um subconjunto do espaço Cantor. No entanto, muitos resultados interessantes relacionam as duas hierarquias. ${\ displaystyle \ Pi _ {n} ^ {0}}$${\ displaystyle X}$${\ displaystyle \ {X \}}$${\ displaystyle \ Pi _ {n} ^ {0}}$

Existem duas maneiras de classificar um subconjunto do espaço Baire na hierarquia aritmética.

• Um subconjunto do espaço Baire tem um subconjunto correspondente do espaço Cantor sob o mapa que leva cada função de a para a função característica de seu gráfico. Um subconjunto de espaço Baire recebe a classificação , ou se e somente se o subconjunto correspondente de espaço Cantor tem a mesma classificação.${\ displaystyle \ omega}$${\ displaystyle \ omega}$${\ displaystyle \ Sigma _ {n} ^ {1}}$${\ displaystyle \ Pi _ {n} ^ {1}}$${\ displaystyle \ Delta _ {n} ^ {1}}$
• Uma definição equivalente da hierarquia analítica no espaço de Baire é dada pela definição da hierarquia analítica das fórmulas usando uma versão funcional da aritmética de segunda ordem; então, a hierarquia analítica em subconjuntos do espaço Cantor pode ser definida a partir da hierarquia no espaço Baire. Esta definição alternativa fornece exatamente as mesmas classificações da primeira definição.

Uma definição paralela é usada para definir a hierarquia aritmética em poderes cartesianos finitos do espaço de Baire ou espaço de Cantor, usando fórmulas com várias variáveis ​​livres. A hierarquia aritmética pode ser definida em qualquer espaço polonês efetivo ; a definição é particularmente simples para o espaço Cantor e o espaço Baire porque eles se encaixam na linguagem da aritmética de segunda ordem comum.

Observe que também podemos definir a hierarquia aritmética de subconjuntos dos espaços de Cantor e Baire em relação a algum conjunto de inteiros. Na verdade negrito é apenas a união de para todos os conjuntos de números inteiros Y . Observe que a hierarquia em negrito é apenas a hierarquia padrão dos conjuntos do Borel . ${\ displaystyle \ mathbf {\ Sigma} _ {n} ^ {0}}$${\ displaystyle \ Sigma _ {n} ^ {0, Y}}$

Extensões e variações

É possível definir a hierarquia aritmética das fórmulas usando uma linguagem estendida com um símbolo de função para cada função recursiva primitiva . Esta variação muda ligeiramente a classificação de , uma vez que o uso de funções recursivas primitivas na aritmética de Peano de primeira ordem requer, em geral, um quantificador existencial ilimitado e, portanto, alguns conjuntos que estão por esta definição estão dentro da definição dada no início deste artigo. e, portanto, todas as classes superiores na hierarquia permanecem inalteradas. ${\ displaystyle \ Sigma _ {0} ^ {0} = \ Pi _ {0} ^ {0} = \ Delta _ {0} ^ {0}}$${\ displaystyle \ Sigma _ {0} ^ {0}}$${\ displaystyle \ Sigma _ {1} ^ {0}}$${\ displaystyle \ Sigma _ {1} ^ {0}}$

Uma variação mais semântica da hierarquia pode ser definida em todas as relações finitárias nos números naturais; a seguinte definição é usada. Cada relação computável é definida para ser . As classificações e são definidas indutivamente com as seguintes regras. ${\ displaystyle \ Sigma _ {0} ^ {0} = \ Pi _ {0} ^ {0} = \ Delta _ {0} ^ {0}}$${\ displaystyle \ Sigma _ {n} ^ {0}}$${\ displaystyle \ Pi _ {n} ^ {0}}$

• Se a relação for, então a relação é definida para ser${\ displaystyle R (n_ {1}, \ ldots, n_ {l}, m_ {1}, \ ldots, m_ {k}) \,}$${\ displaystyle \ Sigma _ {n} ^ {0}}$${\ displaystyle S (n_ {1}, \ ldots, n_ {l}) = \ forall m_ {1} \ cdots \ forall m_ {k} R (n_ {1}, \ ldots, n_ {l}, m_ { 1}, \ ldots, m_ {k})}$${\ displaystyle \ Pi _ {n + 1} ^ {0}}$
• Se a relação for, então a relação é definida para ser${\ displaystyle R (n_ {1}, \ ldots, n_ {l}, m_ {1}, \ ldots, m_ {k}) \,}$${\ displaystyle \ Pi _ {n} ^ {0}}$${\ displaystyle S (n_ {1}, \ ldots, n_ {l}) = \ existe m_ {1} \ cdots \ existe m_ {k} R (n_ {1}, \ ldots, n_ {l}, m_ { 1}, \ ldots, m_ {k})}$${\ displaystyle \ Sigma _ {n + 1} ^ {0}}$

Esta variação altera ligeiramente a classificação de alguns conjuntos. Em particular, como uma classe de conjuntos (definível pelas relações na classe), é idêntico ao que o último foi anteriormente definido. Ele pode ser estendido para cobrir relações finitárias nos números naturais, espaço de Baire e espaço de Cantor. ${\ displaystyle \ Sigma _ {0} ^ {0} = \ Pi _ {0} ^ {0} = \ Delta _ {0} ^ {0}}$${\ displaystyle \ Delta _ {1} ^ {0}}$

Significado da notação

Os significados a seguir podem ser atribuídos à notação para a hierarquia aritmética nas fórmulas.

O subscrito nos símbolos e indica o número de alternâncias de blocos de quantificadores de números universais e existenciais que são usados ​​em uma fórmula. Além disso, o bloco mais externo é existencial nas fórmulas e universal nas fórmulas. ${\ displaystyle n}$${\ displaystyle \ Sigma _ {n} ^ {0}}$${\ displaystyle \ Pi _ {n} ^ {0}}$${\ displaystyle \ Sigma _ {n} ^ {0}}$${\ displaystyle \ Pi _ {n} ^ {0}}$

O sobrescrito nos símbolos , e indica o tipo dos objetos que estão sendo quantificados. Os objetos do tipo 0 são números naturais e os objetos do tipo são funções que mapeiam o conjunto de objetos do tipo para os números naturais. A quantificação sobre objetos de tipo superior, como funções de números naturais a números naturais, é descrita por um sobrescrito maior que 0, como na hierarquia analítica . O sobrescrito 0 indica quantificadores sobre números, o sobrescrito 1 indicaria quantificação sobre funções de números para números (objetos do tipo 1), o sobrescrito 2 corresponderia à quantificação sobre funções que pegam um objeto do tipo 1 e retornam um número, e assim por diante. ${\ displaystyle 0}$${\ displaystyle \ Sigma _ {n} ^ {0}}$${\ displaystyle \ Pi _ {n} ^ {0}}$${\ displaystyle \ Delta _ {n} ^ {0}}$${\ displaystyle i + 1}$${\ displaystyle i}$

Exemplos

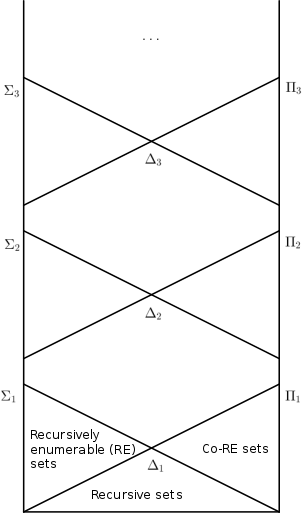
• Os conjuntos de números são aqueles definíveis por uma fórmula da forma onde tem apenas quantificadores limitados. Esses são exatamente os conjuntos recursivamente enumeráveis .${\ displaystyle \ Sigma _ {1} ^ {0}}$${\ displaystyle \ existe n_ {1} \ cdots \ existe n_ {k} \ psi (n_ {1}, \ ldots, n_ {k}, m)}$${\ displaystyle \ psi}$
• O conjunto de números naturais que são índices para máquinas de Turing que calculam funções totais é . Intuitivamente, um índice cai neste conjunto se e somente se para cada "existe um tal que a máquina de Turing com índice para na entrada após as etapas". Uma prova completa mostraria que a propriedade exibida entre aspas na frase anterior é definível em a linguagem da aritmética de Peano por uma fórmula.${\ displaystyle \ Pi _ {2} ^ {0}}$${\ displaystyle e}$${\ displaystyle m}$${\ displaystyle s}$${\ displaystyle e}$${\ displaystyle m}$${\ displaystyle s}$${\ displaystyle \ Sigma _ {1} ^ {0}}$
• Cada subconjunto de espaço Baire ou espaço Cantor é um conjunto aberto na topologia usual do espaço. Além disso, para qualquer conjunto desse tipo, há uma enumeração computável dos números de Gödel dos conjuntos abertos básicos cuja união é o conjunto original. Por esse motivo, os conjuntos às vezes são chamados de efetivamente abertos . Da mesma forma, todos os conjuntos são fechados e os conjuntos às vezes são chamados de efetivamente fechados .${\ displaystyle \ Sigma _ {1} ^ {0}}$${\ displaystyle \ Sigma _ {1} ^ {0}}$${\ displaystyle \ Pi _ {1} ^ {0}}$${\ displaystyle \ Pi _ {1} ^ {0}}$
• Cada subconjunto aritmético do espaço Cantor ou espaço Baire é um conjunto Borel . A hierarquia lightface do Borel estende a hierarquia aritmética para incluir conjuntos adicionais do Borel. Por exemplo, cada subconjunto do espaço Cantor ou Baire é um conjunto (ou seja, um conjunto que é igual à interseção de muitos conjuntos abertos contáveis). Além disso, cada um desses conjuntos abertos é e a lista de números de Gödel desses conjuntos abertos tem uma enumeração computável. Se for uma fórmula com uma variável de conjunto livre X e variáveis ​​de número livre, então o conjunto é a interseção dos conjuntos da forma como n intervalos sobre o conjunto de números naturais.${\ displaystyle \ Pi _ {2} ^ {0}}$${\ displaystyle G _ {\ delta}}$${\ displaystyle \ Sigma _ {1} ^ {0}}$${\ displaystyle \ phi (X, n, m)}$${\ displaystyle \ Sigma _ {0} ^ {0}}$${\ displaystyle n, m}$${\ displaystyle \ Pi _ {2} ^ {0}}$${\ displaystyle \ {X \ mid \ forall n \ existe m \ phi (X, n, m) \}}$${\ displaystyle \ Sigma _ {1} ^ {0}}$${\ displaystyle \ {X \ mid \ exists m \ phi (X, n, m) \}}$
• As fórmulas podem ser verificadas examinando todos os casos um a um, o que é possível porque todos os seus quantificadores são limitados. O tempo para isso é polinomial em seus argumentos (por exemplo, polinomial em n para ); assim, seus problemas de decisão correspondentes são incluídos em E (já que n é exponencial em seu número de bits). Isso não é mais válido em definições alternativas de , que permitem o uso de funções recursivas primitivas, pois agora os quantificadores podem ser limitados por qualquer função recursiva primitiva dos argumentos.${\ displaystyle \ Sigma _ {0} ^ {0} = \ Pi _ {0} ^ {0} = \ Delta _ {0} ^ {0}}$${\ displaystyle \ varphi (n)}$${\ displaystyle \ Sigma _ {0} ^ {0} = \ Pi _ {0} ^ {0} = \ Delta _ {0} ^ {0}}$
• As fórmulas sob uma definição alternativa, que permite o uso de funções recursivas primitivas com quantificadores limitados, correspondem a conjuntos de inteiros da forma de uma função recursiva primitiva f . Isso ocorre porque permitir quantificador limitado não acrescenta nada à definição: para um f primitivo recursivo , é igual a e é igual a ; com recursão de curso de valores, cada um deles pode ser definido por uma única função de recursão primitiva.${\ displaystyle \ Sigma _ {0} ^ {0} = \ Pi _ {0} ^ {0} = \ Delta _ {0} ^ {0}}$${\ displaystyle \ {n: f (n) = 0 \}}$${\ displaystyle \ forall k <n: f (k) = 0}$${\ displaystyle f (0) + f (1) + ... f (n) = 0}$${\ displaystyle \ existe k <n: f (k) = 0}$${\ displaystyle f (0) * f (1) * ... f (n) = 0}$

Propriedades

As propriedades a seguir são válidas para a hierarquia aritmética de conjuntos de números naturais e a hierarquia aritmética de subconjuntos do espaço de Cantor ou Baire.

• As coleções e são fechadas sob uniões finitas e interseções finitas de seus respectivos elementos.${\ displaystyle \ Pi _ {n} ^ {0}}$${\ displaystyle \ Sigma _ {n} ^ {0}}$
• Um conjunto é se e somente se seu complemento for . Um conjunto é se e somente se o conjunto for ambos e , caso em que seu complemento também será .${\ displaystyle \ Sigma _ {n} ^ {0}}$${\ displaystyle \ Pi _ {n} ^ {0}}$${\ displaystyle \ Delta _ {n} ^ {0}}$${\ displaystyle \ Sigma _ {n} ^ {0}}$${\ displaystyle \ Pi _ {n} ^ {0}}$${\ displaystyle \ Delta _ {n} ^ {0}}$
• As inclusões e espera para todos . Assim, a hierarquia não entra em colapso. Esta é uma consequência direta do teorema de Post .${\ displaystyle \ Pi _ {n} ^ {0} \ subsetneq \ Pi _ {n + 1} ^ {0}}$${\ displaystyle \ Sigma _ {n} ^ {0} \ subsetneq \ Sigma _ {n + 1} ^ {0}}$${\ displaystyle n}$
• As inclusões , e espera por .${\ displaystyle \ Delta _ {n} ^ {0} \ subsetneq \ Pi _ {n} ^ {0}}$${\ displaystyle \ Delta _ {n} ^ {0} \ subsetneq \ Sigma _ {n} ^ {0}}$${\ displaystyle \ Sigma _ {n} ^ {0} \ cup \ Pi _ {n} ^ {0} \ subsetneq \ Delta _ {n + 1} ^ {0}}$${\ displaystyle n \ geq 1}$

• Por exemplo, para uma máquina de Turing universal T, o conjunto de pares (n, m) tal que T para em n, mas não em m, está em (sendo computável com um oráculo para o problema da parada), mas não em ,.${\ displaystyle \ Delta _ {2} ^ {0}}$${\ displaystyle \ Sigma _ {1} ^ {0} \ cup \ Pi _ {1} ^ {0}}$
• ${\ displaystyle \ Sigma _ {0} ^ {0} = \ Pi _ {0} ^ {0} = \ Delta _ {0} ^ {0} = \ Sigma _ {0} ^ {0} \ xícara \ Pi _ {0} ^ {0} \ subset \ Delta _ {1} ^ {0}}$. A inclusão é estrita pela definição dada neste artigo, mas uma identidade com se mantém sob uma das variações da definição dada acima .${\ displaystyle \ Delta _ {1} ^ {0}}$

Relação com máquinas de Turing

Conjuntos computáveis

Se S é um conjunto computável de Turing , então S e seu complemento são recursivamente enumeráveis ​​(se T é uma máquina de Turing dando 1 para entradas em S e 0, caso contrário, podemos construir uma máquina de Turing parando apenas no primeiro, e outra parando apenas neste último).

Pelo teorema de Post , tanto S quanto seu complemento estão em . Isso significa que S está dentro e dentro e, portanto, está dentro . ${\ displaystyle \ Sigma _ {1} ^ {0}}$${\ displaystyle \ Sigma _ {1} ^ {0}}$${\ displaystyle \ Pi _ {1} ^ {0}}$${\ displaystyle \ Delta _ {1} ^ {0}}$

De modo semelhante, para cada conjunto S , S e o seu complemento estão em e são, por conseguinte, (pelo teorema de Mensagem ) recursivamente enumeráveis por algumas máquinas de Turing T ₁ e T ₂ , respectivamente. Para cada número n, exatamente uma dessas paradas. Podemos, portanto, construir uma máquina T Turing que alterna entre t ₁ e t ₂ , de paragem e que regressam 1, quando o primeiro paragens ou suspensão e retornam 0 quando o último pára. Assim, T para a cada n e retorna se está em S, então S é computável. ${\ displaystyle \ Delta _ {1} ^ {0}}$${\ displaystyle \ Sigma _ {1} ^ {0}}$

Resumo dos principais resultados

Os conjuntos computáveis ​​de Turing de números naturais são exatamente os conjuntos no nível da hierarquia aritmética. Os conjuntos recursivamente enumeráveis ​​são exatamente os conjuntos no nível . ${\ displaystyle \ Delta _ {1} ^ {0}}$${\ displaystyle \ Sigma _ {1} ^ {0}}$

Nenhuma máquina oráculo é capaz de resolver seu próprio problema de parada (aplica-se uma variação da prova de Turing). O problema da parada para um oráculo de fato se instala . ${\ displaystyle \ Delta _ {n} ^ {0, Y}}$${\ displaystyle \ Sigma _ {n + 1} ^ {0, Y}}$

O teorema de Post estabelece uma conexão estreita entre a hierarquia aritmética de conjuntos de números naturais e os graus de Turing . Em particular, estabelece os seguintes fatos para todo n ≥ 1:

• O conjunto (o n ° de Turing salto do conjunto vazio) é muitas uma completa em .${\ displaystyle \ emptyset ^ {(n)}}$${\ displaystyle \ Sigma _ {n} ^ {0}}$
• O conjunto é completo em muitos e um .${\ displaystyle \ mathbb {N} \ setminus \ emptyset ^ {(n)}}$${\ displaystyle \ Pi _ {n} ^ {0}}$
• O conjunto é Turing completa em .${\ displaystyle \ emptyset ^ {(n-1)}}$${\ displaystyle \ Delta _ {n} ^ {0}}$

A hierarquia polinomial é uma versão "viável de recursos limitados" da hierarquia aritmética na qual limites de comprimento polinomial são colocados nos números envolvidos (ou, equivalentemente, limites de tempo polinomial são colocados nas máquinas de Turing envolvidas). Fornece uma classificação mais precisa de alguns conjuntos de números naturais que estão no nível da hierarquia aritmética. ${\ displaystyle \ Delta _ {1} ^ {0}}$

Relação com outras hierarquias

Veja também

• Hierarquia Lévy
• Hierarquia (matemática)
• Lógica de interpretabilidade
• Hierarquia polinomial

Referências