Funções elípticas de Jacobi - Jacobi elliptic functions

Em matemática , as funções elípticas de Jacobi são um conjunto de funções elípticas básicas e funções teta auxiliares que são de importância histórica. Eles são encontrados na descrição do movimento de um pêndulo (ver também pêndulo (matemática) ), bem como no projeto de filtros elípticos eletrônicos . Enquanto as funções trigonométricas são definidas com referência a um círculo, as funções elípticas de Jacobi são uma generalização que se refere a outras seções cônicas , a elipse em particular. A relação com as funções trigonométricas está contida na notação, por exemplo, pela notação correspondente${\ displaystyle \ operatorname {sn}}$para . As funções elípticas de Jacobi são usadas com mais frequência em problemas práticos do que as funções elípticas de Weierstrass , pois não requerem noções de análise complexa para serem definidas e / ou compreendidas. Eles foram apresentados por Carl Gustav Jakob Jacobi  ( 1829 ). ${\ displaystyle \ sin}$

Visão geral

O retângulo fundamental no plano complexo de ${\ displaystyle u}$

Há doze funções elípticas de Jacobi denotados por , onde e são qualquer uma das letras , , , e . (Funções da forma são trivialmente definidas como unidade para completude notacional.) É o argumento e é o parâmetro, ambos os quais podem ser complexos. ${\ displaystyle \ operatorname {pq} (u, m)}$${\ displaystyle \ mathrm {p}}$${\ displaystyle \ mathrm {q}}$${\ displaystyle \ mathrm {c}}$${\ displaystyle \ mathrm {s}}$${\ displaystyle \ mathrm {n}}$${\ displaystyle \ mathrm {d}}$${\ displaystyle \ operatorname {pp} (u, m)}$${\ displaystyle u}$${\ displaystyle m}$

No plano complexo do argumento , as doze funções formam uma rede repetitiva de pólos e zeros simples . Dependendo da função, um paralelogramo de repetição, ou célula unitária, terá os lados de comprimento ou sobre o eixo real, e ou sobre o eixo imaginário, onde e são conhecidos como os períodos trimestre com sendo o integral elíptica do primeiro tipo. A natureza da célula unitária pode ser determinada inspecionando o "retângulo auxiliar" (geralmente um paralelogramo), que é um retângulo formado pela origem em um canto e como o canto diagonalmente oposto. Como no diagrama, os quatro cantos do retângulo auxiliares são nomeados , , , e , indo sentido anti-horário a partir da origem. A função terá um zero na esquina e um pólo na esquina. As doze funções correspondem às doze maneiras de organizar esses pólos e zeros nos cantos do retângulo. ${\ displaystyle u}$${\ displaystyle 2K}$${\ displaystyle 4K}$${\ displaystyle 2K '}$${\ displaystyle 4K '}$${\ displaystyle K = K (m)}$${\ displaystyle K '= K (1-m)}$${\ displaystyle K (\ cdot)}$${\ displaystyle (0,0)}$${\ displaystyle (K, K ')}$${\ displaystyle \ mathrm {s}}$${\ displaystyle \ mathrm {c}}$${\ displaystyle \ mathrm {d}}$${\ displaystyle \ mathrm {n}}$${\ displaystyle \ operatorname {pq} (u, m)}$${\ displaystyle \ mathrm {p}}$${\ displaystyle \ mathrm {q}}$

Quando o argumento e o parâmetro são reais, com , e será real e o paralelogramo auxiliar será de fato um retângulo, e as funções elípticas de Jacobi serão todas avaliadas como reais na reta real. ${\ displaystyle u}$${\ displaystyle m}$${\ displaystyle 0 <m <1}$${\ displaystyle K}$${\ displaystyle K '}$

Matematicamente, as funções elípticas Jacobianas são funções meromórficas duplamente periódicas no plano complexo . Como são duplamente periódicos, eles faturam por meio de um toro - na verdade, seu domínio pode ser considerado um toro, assim como o cosseno e o seno são definidos em um círculo. Em vez de termos apenas um círculo, agora temos o produto de dois círculos, um real e outro imaginário. O plano complexo pode ser substituído por um toro complexo . A circunferência do primeiro círculo é e o segundo , onde e são os trimestres . Cada função tem dois zeros e dois pólos em posições opostas no toro. Entre os pontos , , , há um zero e um pólo. ${\ displaystyle 4K}$${\ displaystyle 4K '}$${\ displaystyle K}$${\ displaystyle K '}$${\ displaystyle 0}$${\ displaystyle K}$${\ displaystyle K + iK '}$${\ displaystyle iK '}$

As funções elípticas Jacobianas são então as funções meromórficas duplamente periódicas únicas que satisfazem as três propriedades a seguir:

• Há um zero simples no canto e um poste simples no canto  .${\ displaystyle \ mathrm {p}}$${\ displaystyle \ mathrm {q}}$
• O passo de a é igual à metade do período da função ; ou seja, a função é periódica na direção , com o período sendo duas vezes a distância de para . A função também é periódica nas outras duas direções, com um período tal que a distância de um dos outros cantos é um quarto de período.${\ displaystyle \ mathrm {p}}$${\ displaystyle \ mathrm {q}}$${\ displaystyle \ operatorname {pq} u}$${\ displaystyle \ operatorname {pq} u}$${\ displaystyle \ operatorname {pq}}$${\ displaystyle \ mathrm {p}}$${\ displaystyle \ mathrm {q}}$${\ displaystyle \ operatorname {pq} u}$${\ displaystyle \ mathrm {p}}$
• Se a função for expandida em termos de em um dos cantos, o termo principal na expansão terá um coeficiente de  . Em outras palavras, o termo principal da expansão de no canto é ; o termo principal da expansão no canto é , e o termo principal de uma expansão nos outros dois cantos é  .${\ displaystyle \ operatorname {pq} u}$${\ displaystyle u}$${\ displaystyle 1}$${\ displaystyle \ operatorname {pq} u}$${\ displaystyle \ mathrm {p}}$${\ displaystyle u}$${\ displaystyle \ mathrm {q}}$${\ displaystyle u ^ {- 1}}$${\ displaystyle 1}$

Função elíptica de Jacobi ${\ displaystyle \ operatorname {sn}}$

Função elíptica de Jacobi ${\ displaystyle \ operatorname {cn}}$

Função elíptica de Jacobi ${\ displaystyle \ operatorname {dn}}$

Função elíptica de Jacobi ${\ displaystyle \ operatorname {sc}}$

Gráficos de quatro funções elípticas de Jacobi no plano complexo de , ilustrando seu comportamento periódico duplo. Imagens geradas usando uma versão do método de coloração de domínio . Todos têm valores do parâmetro iguais a .${\ displaystyle u}$${\ displaystyle k}$${\ displaystyle 0.8}$

Notação

As funções elípticas podem ser fornecidas em uma variedade de notações, o que pode tornar o assunto desnecessariamente confuso. As funções elípticas são funções de duas variáveis. A primeira variável pode ser dada em termos de amplitude , ou mais comumente, em termos de dado abaixo. A segunda variável pode ser dada em termos do parâmetro , ou como o módulo elíptico , onde , ou em termos do ângulo modular , onde . Os complementos de e são definidos como e . Esses quatro termos são usados ​​a seguir sem comentários para simplificar várias expressões. ${\ displaystyle \ varphi}$${\ displaystyle u}$ ${\ displaystyle m}$ ${\ displaystyle k}$${\ displaystyle k ^ {2} = m}$ ${\ displaystyle \ alpha}$${\ displaystyle m = \ sin ^ {2} \ alpha}$${\ displaystyle k}$${\ displaystyle m}$${\ displaystyle m '= 1-m}$${\ textstyle k '= {\ sqrt {m'}}}$

As funções elípticas doze Jacobi são geralmente escrita como onde e são qualquer uma das letras , , , e . Funções da forma são trivialmente definidas como unidade para completude notacional. As funções "principais" são geralmente consideradas , e a partir das quais todas as outras funções podem ser derivadas e as expressões são frequentemente escritas apenas em termos dessas três funções, no entanto, várias simetrias e generalizações são frequentemente mais convenientemente expressas usando o conjunto completo. (Esta notação é devida a Gudermann e Glaisher e não é a notação original de Jacobi.) ${\ displaystyle \ operatorname {pq} (u, m)}$${\ displaystyle \ mathrm {p}}$${\ displaystyle \ mathrm {q}}$${\ displaystyle \ mathrm {c}}$${\ displaystyle \ mathrm {s}}$${\ displaystyle \ mathrm {n}}$${\ displaystyle \ mathrm {d}}$${\ displaystyle \ operatorname {pp} (u, m)}$${\ displaystyle \ operatorname {cn} (u, m)}$${\ displaystyle \ operatorname {sn} (u, m)}$${\ displaystyle \ operatorname {dn} (u, m)}$

O parâmetro

As funções são notacionalmente relacionadas entre si pela regra de multiplicação: (argumentos suprimidos)

${\ displaystyle \ operatorname {pq} \ cdot \ operatorname {p'q '} = \ operatorname {pq'} \ cdot \ operatorname {p'q}}$

a partir do qual outros relacionamentos comumente usados ​​podem ser derivados:

${\ displaystyle {\ frac {\ operatorname {pr}} {\ operatorname {qr}}} = \ operatorname {pq}}$

${\ displaystyle \ operatorname {pr} \ cdot \ operatorname {rq} = \ operatorname {pq}}$

${\ displaystyle {\ frac {1} {\ operatorname {qp}}} = \ operatorname {pq}}$

A regra de multiplicação segue imediatamente da identificação das funções elípticas com as funções de Neville theta

${\ displaystyle \ operatorname {pq} (u, m) = {\ frac {\ theta _ {\ operatorname {p}} (u, m)} {\ theta _ {\ operatorname {q}} (u, m) }}}$

Definição como inversos de integrais elípticos

Modelo de amplitude (medido ao longo do eixo vertical) em função das variáveis ​​independentes u e k

A definição acima, em termos das funções meromórficas únicas que satisfazem certas propriedades, é bastante abstrata. Existe uma definição mais simples, mas completamente equivalente, dando as funções elípticas como inversas da integral elíptica incompleta do primeiro tipo. Deixar

${\ displaystyle u = \ int _ {0} ^ {\ varphi} {\ frac {\ mathrm {d} \ theta} {\ sqrt {1-m \ sin ^ {2} \ theta}}} \ ,.}$

Então, o seno elíptico sn  u (latim: sinus amplitudinis ) é dado por

${\ displaystyle \ operatorname {sn} u = \ sin \ varphi \,}$

e o cosseno elíptico cn  u (latim: cosinus amplitudinis ) é dado por

${\ displaystyle \ operatorname {cn} u = \ cos \ varphi}$

e a amplitude delta dn  u (latim: delta amplitudinis )

${\ displaystyle \ operatorname {dn} u = {\ sqrt {1-m \ sin ^ {2} \ varphi}} \ ,.}$

Aqui, o ângulo é chamado de amplitude . Na ocasião, é chamada de amplitude delta . Acima, o valor é um parâmetro livre, geralmente considerado real, e, portanto, as funções elípticas podem ser consideradas como sendo dadas por duas variáveis, a amplitude e o parâmetro  . ${\ displaystyle \ varphi}$${\ displaystyle \ operatorname {dn} u = \ Delta (u)}$${\ displaystyle m}$${\ displaystyle 0 \ leq m \ leq 1}$${\ displaystyle \ varphi}$${\ displaystyle m}$

As nove funções elípticas restantes são facilmente construídas a partir das três anteriores e são fornecidas em uma seção abaixo.

Observe que quando , esse u então é igual ao período do trimestre . ${\ displaystyle \ varphi = \ pi / 2}$ ${\ displaystyle K}$

Definição como trigonometria: a elipse de Jacobi

Gráfico da elipse de Jacobi ( x ² + y ² / b ² = 1, b real) e as doze funções elípticas de Jacobi pq (u, m) para valores particulares do ângulo φ e parâmetro b . A curva sólida é a elipse, com m = 1-1 / b ² e u = F (φ, m) onde F (.,.) É a integral elíptica de primeiro tipo. A curva pontilhada é o círculo unitário. As linhas tangentes do círculo e da elipse em x = cd cruzando o eixo x em dc são mostradas em cinza claro.

${\ displaystyle \ cos \ varphi, \ sin \ varphi}$são definidos no círculo unitário, com raio r  = 1 e comprimento do arco do ângulo do círculo unitário medido a partir do eixo x positivo . Da mesma forma, as funções elípticas de Jacobi são definidas na elipse unitária, com a  = 1. Seja ${\ displaystyle \ varphi =}$

${\ displaystyle {\ begin {alinhados} & x ^ {2} + {\ frac {y ^ {2}} {b ^ {2}}} = 1, \ quad b> 1, \\ & m = 1 - {\ frac {1} {b ^ {2}}}, \ quad 0 <m <1, \\ & x = r \ cos \ varphi, \ quad y = r \ sin \ varphi \ end {alinhado}}}$

então:

${\ displaystyle r (\ varphi, m) = {\ frac {1} {\ sqrt {1-m \ sin ^ {2} \ varphi}}} \ ,.}$

Para cada ângulo, o parâmetro ${\ displaystyle \ varphi}$

${\ displaystyle u = u (\ varphi, m) = \ int _ {0} ^ {\ varphi} r (\ theta, m) \, d \ theta}$

é calculado. No círculo unitário ( ), haveria um comprimento de arco. Embora não pareça carregar uma interpretação geométrica direta no caso elíptico, acaba sendo o parâmetro que entra na definição das funções elípticas. Na verdade, seja um ponto na elipse e seja o ponto onde o círculo unitário intercepta a linha entre e a origem . Em seguida, as relações familiares do círculo unitário: ${\ displaystyle a = b = 1}$${\ displaystyle u}$${\ displaystyle u}$${\ displaystyle P = (x, y) = (r \ cos \ varphi, r \ sin \ varphi)}$${\ displaystyle P '= (x', y ') = (\ cos \ varphi, \ sin \ varphi)}$${\ displaystyle P}$${\ displaystyle O}$

${\ displaystyle x '= \ cos \ varphi, \ quad y' = \ sin \ varphi}$

leia para ver a elipse:

${\ displaystyle x '= \ operatorname {cn} (u, m), \ quad y' = \ operatorname {sn} (u, m).}$

Assim, as projecções do ponto de intersecção da linha com o círculo unitário no X - e y -axes são simplesmente e . Essas projeções podem ser interpretadas como 'definição como trigonometria'. Resumidamente: ${\ displaystyle P '}$${\ displaystyle OP}$${\ displaystyle \ operatorname {cn} (u, m)}$${\ displaystyle \ operatorname {sn} (u, m)}$

${\ displaystyle \ operatorname {cn} (u, m) = {\ frac {x} {r (\ varphi, m)}}, \ quad \ operatorname {sn} (u, m) = {\ frac {y} {r (\ varphi, m)}}, \ quad \ operatorname {dn} (u, m) = {\ frac {1} {r (\ varphi, m)}}.}$

Para o valor e do ponto com o parâmetro e obtemos, após inserir a relação: ${\ displaystyle x}$${\ displaystyle y}$${\ displaystyle P}$${\ displaystyle u}$${\ displaystyle m}$

${\ displaystyle r (\ varphi, m) = {\ frac {1} {\ operatorname {dn} (u, m)}}}$

em: que: ${\ displaystyle x = r (\ varphi, m) \ cos (\ varphi), y = r (\ varphi, m) \ sin (\ varphi)}$

${\ displaystyle x = {\ frac {\ operatorname {cn} (u, m)} {\ operatorname {dn} (u, m)}}, \ quad y = {\ frac {\ operatorname {sn} (u, m)} {\ operatorname {dn} (u, m)}}.}$

Os últimos relações para o x - e y -coordena de pontos sobre a unidade de elipse pode ser considerado como generalização das relações para as coordenadas de pontos no círculo unitário. ${\ displaystyle x = \ cos \ varphi, y = \ sin \ varphi}$

A tabela a seguir resume as expressões para todas as funções elípticas de Jacobi pq (u, m) nas variáveis ​​( x , y , r ) e ( φ , dn) com${\ displaystyle r = {\ sqrt {x ^ {2} + y ^ {2}}}}$

Funções elípticas de Jacobi pq [u, m] como funções de {x, y, r} e {φ, dn}

		q
		c	s	n	d
p
	c	1	${\ displaystyle x / y = \ cot (\ phi)}$	${\ displaystyle x / r = \ cos (\ phi)}$	${\ displaystyle x = \ cos (\ phi) / \ operatorname {dn}}$
	s	${\ displaystyle y / x = \ tan (\ phi)}$	1	${\ displaystyle y / r = \ sin (\ phi)}$	${\ displaystyle y = \ sin (\ phi) / \ operatorname {dn}}$
	n	${\ displaystyle r / x = \ sec (\ phi)}$	${\ displaystyle r / y = \ csc (\ phi)}$	1	${\ displaystyle r = 1 / \ operatorname {dn}}$
	d	${\ displaystyle 1 / x = \ operatorname {dn} \ sec (\ phi)}$	${\ displaystyle 1 / y = \ operatorname {dn} \ csc (\ phi)}$	${\ displaystyle 1 / r = \ operatorname {dn}}$	1

Definição em termos de funções teta de Jacobi

De forma equivalente, as funções elípticas de Jacobi podem ser definidas em termos de suas funções teta . Se abreviarmos como , e respectivamente como (as constantes teta ), então o módulo elíptico k da função theta é . Se definirmos , temos ${\ displaystyle \ vartheta (0; \ tau)}$${\ displaystyle \ vartheta}$${\ displaystyle \ vartheta _ {01} (0; \ tau), \ vartheta _ {10} (0; \ tau), \ vartheta _ {11} (0; \ tau)}$${\ displaystyle \ vartheta _ {01}, \ vartheta _ {10}, \ vartheta _ {11}}$ ${\ displaystyle k = \ left ({\ vartheta _ {10} \ over \ vartheta} \ right) ^ {2}}$${\ displaystyle u = \ pi \ vartheta ^ {2} z}$

${\ displaystyle {\ begin {alinhado} \ operatorname {sn} (u; k) & = - {\ vartheta \ vartheta _ {11} (z; \ tau) \ over \ vartheta _ {10} \ vartheta _ {01 } (z; \ tau)} \\ [7pt] \ operatorname {cn} (u; k) & = {\ vartheta _ {01} \ vartheta _ {10} (z; \ tau) \ over \ vartheta _ { 10} \ vartheta _ {01} (z; \ tau)} \\ [7pt] \ operatorname {dn} (u; k) & = {\ vartheta _ {01} \ vartheta (z; \ tau) \ over \ vartheta \ vartheta _ {01} (z; \ tau)} \ end {alinhado}}}$

Como as funções de Jacobi são definidas em termos do módulo elíptico , precisamos inverter isso e encontrar em termos de . Partimos da , o módulo complementar . Em função disso é ${\ displaystyle k (\ tau)}$${\ displaystyle \ tau}$${\ displaystyle k}$${\ displaystyle k '= {\ sqrt {1-k ^ {2}}}}$${\ displaystyle \ tau}$

${\ displaystyle k '(\ tau) = \ left ({\ vartheta _ {01} \ over \ vartheta} \ right) ^ {2}.}$

Vamos primeiro definir

${\ displaystyle \ ell = {1 \ over 2} {1 - {\ sqrt {k '}} \ over 1 + {\ sqrt {k'}}} = {1 \ over 2} {\ vartheta - \ vartheta _ {01} \ over \ vartheta + \ vartheta _ {01}}.}$

Em seguida, defina o nome como e expanda como uma série de potências no nome , obtemos ${\ displaystyle q = \ exp (\ pi i \ tau)}$${\ displaystyle \ ell}$${\ displaystyle q}$

${\ displaystyle \ ell = {q + q ^ {9} + q ^ {25} + \ cdots \ over 1 + 2q ^ {4} + 2q ^ {16} + \ cdots}.}$

A reversão da série agora dá

${\ displaystyle q = \ ell +2 \ ell ^ {5} +15 \ ell ^ {9} +150 \ ell ^ {13} +1707 \ ell ^ {17} +20910 \ ell ^ {21} +268616 \ ell ^ {25} + \ cdots.}$

Visto que podemos reduzir ao caso em que a parte imaginária de é maior ou igual a , podemos assumir que o valor absoluto de é menor ou igual a ; para valores tão pequenos, a série acima converge muito rápida e facilmente nos permite encontrar o valor apropriado para . ${\ displaystyle \ tau}$${\ displaystyle {\ sqrt {3}} / 2}$${\ displaystyle q}$${\ displaystyle \ exp (- \ pi {\ sqrt {3}} / 2) \ aproximadamente 0,0658}$${\ displaystyle q}$

Definição em termos de funções Neville theta

As funções elípticas de Jacobi podem ser definidas de forma muito simples usando as funções Theta de Neville :

${\ displaystyle \ operatorname {pq} (u, m) = {\ frac {\ theta _ {\ operatorname {p}} (u, m)} {\ theta _ {\ operatorname {q}} (u, m) }}}$

Simplificações de produtos complicados das funções elípticas de Jacobi são freqüentemente facilitadas usando essas identidades.

Transformações de Jacobi

As transformações imaginárias de Jacobi

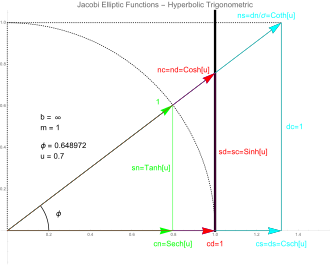
Gráfico da curva de Jacobi degenerada (x ² + y ² / b ² = 1, b = infinito) e as doze funções elípticas de Jacobi pq (u, 1) para um valor particular de ângulo φ. A curva sólida é a elipse degenerada (x ² = 1) com m = 1 e u = F (φ, 1) onde F (.,.) É a integral elíptica do primeiro tipo. A curva pontilhada é o círculo unitário . Como essas são as funções de Jacobi para m = 0 (funções trigonométricas circulares), mas com argumentos imaginários, elas correspondem às seis funções trigonométricas hiperbólicas.

As transformações imaginárias de Jacobi relacionam várias funções da variável imaginária iu ou, de forma equivalente, relações entre vários valores do parâmetro m . Em termos das principais funções:

${\ displaystyle \ operatorname {cn} (u, m) = \ operatorname {nc} (i \, u, 1 \! - \! m)}$

${\ displaystyle \ operatorname {sn} (u, m) = - i \ operatorname {sc} (i \, u, 1 \! - \! m)}$

${\ displaystyle \ operatorname {dn} (u, m) = \ operatorname {dc} (i \, u, 1 \! - \! m)}$

Usando a regra de multiplicação, todas as outras funções podem ser expressas em termos dos três anteriores. As transformações podem ser geralmente escritas como . A tabela a seguir fornece o para o pq especificado ( u, m ). (Os argumentos são suprimidos) ${\ displaystyle \ operatorname {pq} (u, m) = \ gamma _ {\ operatorname {pq}} \ operatorname {pq} '(i \, u, 1 \! - \! m)}$${\ displaystyle \ gamma _ {\ operatorname {pq}} \ operatorname {pq} '(i \, u, 1 \! - \! m)}$${\ displaystyle (i \, u, 1 \! - \! m)}$

Transformações imaginárias de Jacobi ${\ displaystyle \ gamma _ {\ operatorname {pq}} \ operatorname {pq} '(i \, u, 1 \! - \! m)}$

		q
		c	s	n	d
p
	c	1	eu ns	nc	WL
	s	-i sn	1	-i sc	-i sd
	n	cn	eu cs	1	CD
	d	dn	eu ds	dc	1

Uma vez que as funções trigonométricas hiperbólicas são proporcionais às funções trigonométricas circulares com argumentos imaginários, segue-se que as funções de Jacobi produzirão as funções hiperbólicas para m = 1. Na figura, a curva de Jacobi degenerou em duas linhas verticais em x = 1 e x = -1.

As transformações reais de Jacobi

As transformações reais de Jacobi produzem expressões para as funções elípticas em termos com valores alternativos de m . As transformações podem ser geralmente escritas como . A tabela a seguir fornece o para o pq especificado ( u, m ). (Os argumentos são suprimidos) ${\ displaystyle \ operatorname {pq} (u, m) = \ gamma _ {\ operatorname {pq}} \ operatorname {pq} '(k \, u, 1 / m)}$${\ displaystyle \ gamma _ {\ operatorname {pq}} \ operatorname {pq} '(k \, u, 1 / m)}$${\ displaystyle (k \, u, 1 / m)}$

Transformações reais de Jacobi ${\ displaystyle \ gamma _ {\ operatorname {pq}} \ operatorname {pq} '(k \, u, 1 / m)}$

		q
		c	s	n	d
p
	c	1	${\ displaystyle k}$ ds	dn	dc
	s	${\ displaystyle {\ frac {1} {k}}}$ SD	1	${\ displaystyle {\ frac {1} {k}}}$ sn	${\ displaystyle {\ frac {1} {k}}}$ sc
	n	WL	${\ displaystyle k}$ ns	1	nc
	d	CD	${\ displaystyle k}$ cs	cn	1

Outras transformações de Jacobi

As transformações reais e imaginárias de Jacobi podem ser combinadas de várias maneiras para produzir três transformações mais simples. As transformações reais e imaginárias são duas transformações em um grupo ( D ₃ ou grupo anarmônico ) de seis transformações. Se

${\ displaystyle \ mu _ {R} (m) = 1 / m}$

é a transformação para o parâmetro m na transformação real, e

${\ displaystyle \ mu _ {I} (m) = 1-m = m '}$

é a transformação de m na transformação imaginária, então as outras transformações podem ser construídas pela aplicação sucessiva dessas duas transformações básicas, produzindo apenas mais três possibilidades:

${\ displaystyle {\ begin {alinhado} \ mu _ {IR} (m) & = & \ mu _ {I} (\ mu _ {R} (m)) & = & - m '/ m \\\ mu _ {RI} (m) & = & \ mu _ {R} (\ mu _ {I} (m)) & = & 1 / m '\\\ mu _ {RIR} (m) & = & \ mu _ {R} (\ mu _ {I} (\ mu _ {R} (m))) & = & - m / m '\ end {alinhado}}}$

Essas cinco transformações, junto com a transformação de identidade (μ _U (m) = m), geram o grupo de 6 elementos. Com relação às funções elípticas de Jacobi, a transformação geral pode ser expressa usando apenas três funções:

${\ displaystyle \ operatorname {cs} (u, m) = \ gamma _ {i} \ operatorname {cs '} (\ gamma _ {i} u, \ mu _ {i} (m))}$

${\ displaystyle \ operatorname {ns} (u, m) = \ gamma _ {i} \ operatorname {ns '} (\ gamma _ {i} u, \ mu _ {i} (m))}$

${\ displaystyle \ operatorname {ds} (u, m) = \ gamma _ {i} \ operatorname {ds '} (\ gamma _ {i} u, \ mu _ {i} (m))}$

onde i = U, I, IR, R, RI ou RIR, identificando a transformação, γ _i é um fator de multiplicação comum a essas três funções, e o primo indica a função transformada. As outras nove funções transformadas podem ser desenvolvidas a partir das três anteriores. A razão pela qual as funções cs, ns, ds foram escolhidas para representar a transformação é que as outras funções serão proporções dessas três (exceto por seus inversos) e os fatores de multiplicação serão cancelados.

A tabela a seguir lista os fatores de multiplicação para as três funções ps, os m 's transformados e os nomes das funções transformadas para cada uma das seis transformações. (Como de costume, k ² = m, 1-k ² = k ₁ ² = m 'e os argumentos ( ) são suprimidos) ${\ displaystyle \ gamma _ {i} u, \ mu _ {i} (m)}$

Parâmetros para as seis transformações

Transformação i	${\ displaystyle \ gamma _ {i}}$	${\ displaystyle \ mu _ {i} (m)}$	cs '	ns '	ds '
você	1	m	cs	ns	ds
eu	eu	m '	ns	cs	ds
IR	ik	-milímetros	ds	cs	ns
R	k	1 / m	ds	ns	cs
RI	ik 1	1 / m '	ns	ds	cs
RIR	k 1	-milímetros'	cs	ds	ns

Assim, por exemplo, podemos construir a seguinte tabela para a transformação de RIR. A transformação geralmente é escrita (os argumentos são suprimidos) ${\ displaystyle \ operatorname {pq} (u, m) = \ gamma _ {\ operatorname {pq}} \, \ operatorname {pq '} (k' \, u, -m / m ')}$${\ displaystyle (k '\, u, -m / m')}$

A transformação RIR ${\ displaystyle \ gamma _ {\ operatorname {pq}} \, \ operatorname {pq '} (k' \, u, -m / m ')}$

		q
		c	s	n	d
p
	c	1	k 'cs	CD	cn
	s	${\ displaystyle {\ frac {1} {k '}}}$ sc	1	${\ displaystyle {\ frac {1} {k '}}}$ SD	${\ displaystyle {\ frac {1} {k '}}}$ sn
	n	dc	${\ displaystyle k '}$ ds	1	dn
	d	nc	${\ displaystyle k '}$ ns	WL	1

O valor das transformações de Jacobi é que qualquer conjunto de funções elípticas de Jacobi com qualquer parâmetro de valor complexo m pode ser convertido em outro conjunto para o qual 0 <= m <= 1 e, para valores reais de u , os valores da função serão reais .

A hipérbole de Jacobi

Gráfico da hipérbole de Jacobi ( x ² + y ² / b ² = 1, b imaginário) e as doze funções elípticas de Jacobi pq (u, m) para valores particulares do ângulo φ e parâmetro b . A curva sólida é a hipérbole, com m = 1-1 / b ² e u = F (φ, m) onde F (.,.) É a integral elíptica de primeiro tipo. A curva pontilhada é o círculo unitário. Para o triângulo ds-dc, σ = sin (φ) cos (φ) .

Apresentando números complexos, nossa elipse tem uma hipérbole associada:

${\ displaystyle x ^ {2} - {\ frac {y ^ {2}} {b ^ {2}}} = 1}$

da aplicação da transformação imaginária de Jacobi às funções elípticas na equação acima para x e  y .

${\ displaystyle x = {\ frac {1} {\ operatorname {dn} (u, 1-m)}}, \ quad y = {\ frac {\ operatorname {sn} (u, 1-m)} {\ operatorname {dn} (u, 1-m)}}}$

Conclui-se que podemos colocar . Portanto, nossa elipse tem uma elipse dupla com m substituído por 1-m. Isso leva ao toro complexo mencionado na Introdução. Geralmente, m pode ser um número complexo, mas quando m é real em <0, a curva é uma elipse com eixo principal na direção x. Em m = 0, a curva é um círculo e, para 0 <m <1, a curva é uma elipse com o eixo principal na direção y. Em m = 1, a curva degenera em duas linhas verticais em x = + / - 1. Para m> 1, a curva é uma hipérbole. Quando m é complexo, mas não real, x ou y ou ambos são complexos e a curva não pode ser descrita em um diagrama real xy. ${\ displaystyle x = \ operatorname {dn} (u, 1-m), y = \ operatorname {sn} (u, 1-m)}$

Funções menores

Inverter a ordem das duas letras do nome da função resulta nos recíprocos das três funções acima:

${\ displaystyle {\ begin {alinhado} \ operatorname {ns} (u) = {\ frac {1} {\ operatorname {sn} (u)}}, \ qquad \ operatorname {nc} (u) = {\ frac {1} {\ operatorname {cn} (u)}}, \ qquad \ operatorname {nd} (u) = {\ frac {1} {\ operatorname {dn} (u)}}. \ End {alinhado}} }$

Da mesma forma, as proporções das três funções primárias correspondem à primeira letra do numerador seguida pela primeira letra do denominador:

${\ displaystyle {\ begin {alinhado} \ operatorname {sc} (u) = {\ frac {\ operatorname {sn} (u)} {\ operatorname {cn} (u)}}, \ qquad \ operatorname {sd} (u) = {\ frac {\ operatorname {sn} (u)} {\ operatorname {dn} (u)}}, \ qquad \ operatorname {dc} (u) = {\ frac {\ operatorname {dn} ( u)} {\ operatorname {cn} (u)}}, \ qquad \ operatorname {ds} (u) = {\ frac {\ operatorname {dn} (u)} {\ operatorname {sn} (u)}} , \ qquad \ operatorname {cs} (u) = {\ frac {\ operatorname {cn} (u)} {\ operatorname {sn} (u)}}, \ qquad \ operatorname {cd} (u) = {\ frac {\ operatorname {cn} (u)} {\ operatorname {dn} (u)}}. \ end {alinhado}}}$

Mais compactamente, temos

${\ displaystyle \ operatorname {pq} (u) = {\ frac {\ operatorname {pn} (u)} {\ operatorname {qn} (u)}}}$

onde p e q são qualquer uma das letras s, c, d.

Periodicidade, pólos e resíduos

Gráficos da fase para as doze funções elípticas de Jacobi pq (u, m) como um argumento complexo de função u, com pólos e zeros indicados. Os gráficos têm mais de um ciclo completo nas direções real e imaginária com a parte colorida indicando a fase de acordo com a roda de cores no canto inferior direito (que substitui a função dd trivial). Regiões com amplitude abaixo de 1/3 são coloridas de preto, indicando aproximadamente a localização de um zero, enquanto regiões com amplitude acima de 3 são coloridas de branco, indicando aproximadamente a posição de um pólo. Todos os gráficos usam m = 2/3 com K = K (m), K '= K (1-m), K (.) Sendo a integral elíptica completa do primeiro tipo. As setas nos pólos apontam na direção da fase zero. As setas para a direita e para a esquerda indicam resíduos reais positivos e negativos, respectivamente. As setas para cima e para baixo significam resíduos imaginários positivos e negativos, respectivamente.

No plano complexo do argumento u , as funções elípticas de Jacobi formam um padrão repetitivo de pólos (e zeros). Os resíduos dos pólos têm todos a mesma amplitude, diferindo apenas no sinal. Cada função pq (u, m) tem uma função inversa qp (u, m) na qual as posições dos pólos e zeros são trocadas. Os períodos de repetição são geralmente diferentes nas direções real e imaginária, daí o uso do termo "duplamente periódico" para descrevê-los.

A dupla periodicidade das funções elípticas de Jacobi pode ser expressa como:

${\ displaystyle \ operatorname {pq} (u + 2 \ alpha K (m) + 2i \ beta K (1-m) \ ,, \, m) = (- 1) ^ {\ gamma} \ operatorname {pq} (u, m)}$

onde α e β são qualquer par de inteiros. K (.) É a integral elíptica completa de primeiro tipo, também conhecida como período de um quarto . O poder da unidade negativa (γ) é dado na seguinte tabela:

${\ displaystyle \ gamma}$

		q
		c	s	n	d
p
	c	0	β	α + β	α
	s	β	0	α	α + β
	n	α + β	α	0	β
	d	α	α + β	β	0

Quando o fator (-1) ^γ é igual a -1, a equação expressa a quase periodicidade. Quando é igual à unidade, expressa a periodicidade completa. Pode-se ver, por exemplo, que para as entradas contendo apenas α quando α é par, a periodicidade total é expressa pela equação acima, e a função tem períodos completos de 4K (m) e 2iK (1-m). Da mesma forma, as funções com entradas contendo apenas β têm períodos completos de 2K (m) e 4iK (1-m), enquanto aquelas com α + β têm períodos completos de 4K (m) e 4iK (1-m).

No diagrama à direita, que representa uma unidade de repetição para cada função, indicando a fase junto com a localização dos pólos e zeros, podem ser observadas várias regularidades: O inverso de cada função é oposto à diagonal e tem o mesmo tamanho célula unitária, com pólos e zeros trocados. O polo e o arranjo zero no retângulo auxiliar formado por (0,0), (K, 0), (0, K ') e (K, K') estão de acordo com a descrição do pólo e o posicionamento zero descrito em a introdução acima. Além disso, o tamanho dos pólos indicadores ovais brancos é uma medida aproximada da amplitude do resíduo para aquele pólo. Os resíduos dos pólos mais próximos da origem na figura (ou seja, no retângulo auxiliar) estão listados na tabela a seguir:

Resíduos de funções elípticas de Jacobi

		q
		c	s	n	d
p
	c		1	${\ displaystyle - {\ frac {i} {k}}}$	${\ displaystyle - {\ frac {1} {k}}}$
	s	${\ displaystyle - {\ frac {1} {k '}}}$		${\ displaystyle {\ frac {1} {k}}}$	${\ displaystyle - {\ frac {i} {k \, k '}}}$
	n	${\ displaystyle - {\ frac {1} {k '}}}$	1		${\ displaystyle - {\ frac {i} {k '}}}$
	d	-1	1	${\ displaystyle -i}$

Quando aplicável, os pólos deslocados para cima em 2K ou deslocados para a direita em 2K 'têm o mesmo valor, mas com os sinais invertidos, enquanto os diagonalmente opostos têm o mesmo valor. Observe que os pólos e zeros nas bordas esquerda e inferior são considerados parte da célula unitária, enquanto os das bordas superior e direita não são.

Relações entre quadrados das funções

As relações entre os quadrados das funções podem ser derivadas de duas relações básicas (Argumentos ( u , m ) suprimidos):

${\ displaystyle \ operatorname {cn} ^ {2} + \ operatorname {sn} ^ {2} = 1}$

${\ displaystyle \ operatorname {cn} ^ {2} + m '\ operatorname {sn} ^ {2} = \ operatorname {dn} ^ {2}}$

onde m + m '  = 1 e m  =  k ² . Multiplicando por qualquer função da forma nq produz equações mais gerais:

${\ displaystyle \ operatorname {cq} ^ {2} + \ operatorname {sq} ^ {2} = \ operatorname {nq} ^ {2}}$

${\ displaystyle \ operatorname {cq} ^ {2} + m '\ operatorname {sq} ^ {2} = \ operatorname {dq} ^ {2}}$

Com q = d , eles correspondem trigonometricamente às equações do círculo unitário ( ) e da elipse unitária ( ), com x = cd , y = sd e r = nd . Usando a regra de multiplicação, outros relacionamentos podem ser derivados. Por exemplo: ${\ displaystyle x ^ {2} + y ^ {2} = r ^ {2}}$${\ displaystyle x ^ {2} + m'y ^ {2} = 1}$

${\ displaystyle - \ operatorname {dn} ^ {2} + m '= - m \ operatorname {cn} ^ {2} = m \ operatorname {sn} ^ {2} -m}$

${\ displaystyle -m '\ operatorname {nd} ^ {2} + m' = - mm '\ operatorname {sd} ^ {2} = m \ operatorname {cd} ^ {2} -m}$

${\ displaystyle m '\ operatorname {sc} ^ {2} + m' = m '\ operatorname {nc} ^ {2} = \ operatorname {dc} ^ {2} -m}$

${\ displaystyle \ operatorname {cs} ^ {2} + m '= \ operatorname {ds} ^ {2} = \ operatorname {ns} ^ {2} -m}$

Teoremas de adição

As funções satisfazem as duas relações quadradas

${\ displaystyle \ operatorname {cn} ^ {2} (u, k) + \ operatorname {sn} ^ {2} (u, k) = 1, \,}$

${\ displaystyle \ operatorname {dn} ^ {2} (u, k) + k ^ {2} \ operatorname {sn} ^ {2} (u, k) = 1. \,}$

A partir disso, vemos que (cn, sn, dn) parametriza uma curva elíptica que é a interseção das duas quádricas definidas pelas duas equações acima. Agora podemos definir uma lei de grupo para pontos nesta curva pelas fórmulas de adição para as funções de Jacobi

${\ displaystyle {\ begin {alinhado} \ operatorname {cn} (x + y) & = {\ operatorname {cn} (x) \ operatorname {cn} (y) - \ operatorname {sn} (x) \ operatorname { sn} (y) \ operatorname {dn} (x) \ operatorname {dn} (y) \ over {1-k ^ {2} \ operatorname {sn} ^ {2} (x) \ operatorname {sn} ^ { 2} (y)}}, \\ [8pt] \ operatorname {sn} (x + y) & = {\ operatorname {sn} (x) \ operatorname {cn} (y) \ operatorname {dn} (y) + \ operatorname {sn} (y) \ operatorname {cn} (x) \ operatorname {dn} (x) \ over {1-k ^ {2} \ operatorname {sn} ^ {2} (x) \ operatorname { sn} ^ {2} (y)}}, \\ [8pt] \ operatorname {dn} (x + y) & = {\ operatorname {dn} (x) \ operatorname {dn} (y) -k ^ { 2} \ operatorname {sn} (x) \ operatorname {sn} (y) \ operatorname {cn} (x) \ operatorname {cn} (y) \ over {1-k ^ {2} \ operatorname {sn} ^ {2} (x) \ operatorname {sn} ^ {2} (y)}}. \ End {alinhado}}}$

As fórmulas de ângulo duplo podem ser facilmente derivadas das equações acima, definindo x = y . As fórmulas de meio ângulo são todas no formato:

${\ displaystyle \ operatorname {pq} ({\ tfrac {1} {2}} u, m) ^ {2} = f _ {\ mathrm {p}} / f _ {\ mathrm {q}}}$

Onde:

${\ displaystyle f _ {\ mathrm {c}} = \ operatorname {cn} (u, m) + \ operatorname {dn} (u, m)}$

${\ displaystyle f _ {\ mathrm {s}} = 1- \ operatorname {cn} (u, m)}$

${\ displaystyle f _ {\ mathrm {n}} = 1 + \ operatorname {dn} (u, m)}$

${\ displaystyle f _ {\ mathrm {d}} = (1+ \ operatorname {dn} (u, m)) - m (1- \ operatorname {cn} (u, m))}$

Valores especiais

Valores para a redução de K:

${\ displaystyle \ operatorname {sn} \ left [{\ tfrac {1} {2}} K (k); k \ right] = {\ frac {1} {\ sqrt {1 + {\ sqrt {1-k ^ {2}}}}}}}$e e${\ displaystyle \ operatorname {cn} \ left [{\ tfrac {1} {2}} K (k); k \ right] = {\ frac {\ sqrt [{4}] {1-k ^ {2} }} {\ sqrt {1 + {\ sqrt {1-k ^ {2}}}}}}}$${\ displaystyle \ operatorname {dn} \ left [{\ tfrac {1} {2}} K (k); k \ right] = {\ sqrt [{4}] {1-k ^ {2}}}}$

Valores para os terços de K:

${\ displaystyle \ operatorname {sn} \ left [{\ frac {1} {3}} K \ left ({\ frac {x ^ {3}} {{\ sqrt {x ^ {6} +1}} + 1}} \ right); {\ frac {x ^ {3}} {{\ sqrt {x ^ {6} +1}} + 1}} \ right] = {\ frac {{\ sqrt {2 {\ sqrt {x ^ {4} -x ^ {2} +1}} - x ^ {2} +2}} + {\ sqrt {x ^ {2} +1}} - 1} {{\ sqrt {2 {\ sqrt {x ^ {4} -x ^ {2} +1}} - x ^ {2} +2}} + {\ sqrt {x ^ {2} +1}} + 1}}}$

Para obter x ^ 3, você deve obter a tangente de duas vezes o arco-tangente do módulo.

Além disso, esta equação leva ao valor sn do terço de K:

${\ displaystyle k ^ {2} s ^ {4} -2k ^ {2} s ^ {3} + 2s-1 = 0}$

${\ displaystyle s = \ operatorname {sn} \ left [{\ tfrac {1} {3}} K (k); k \ right]}$

Essas equações levam aos outros valores das Funções Jacobi:

${\ displaystyle \ operatorname {cn} \ left [{\ tfrac {2} {3}} K (k); k \ right] = 1- \ operatorname {sn} \ left [{\ tfrac {1} {3} } K (k); k \ direita]}$

${\ displaystyle \ operatorname {dn} \ left [{\ tfrac {2} {3}} K (k); k \ right] = 1 / \ operatorname {sn} \ left [{\ tfrac {1} {3} } K (k); k \ direita] -1}$

Valores para os quintos de K:

A equação a seguir tem a seguinte solução:

${\ displaystyle 4k ^ {2} x ^ {6} + 8k ^ {2} x ^ {5} +2 (1-k ^ {2}) ^ {2} x- (1-k ^ {2}) ^ {2} = 0}$

${\ displaystyle x = {\ frac {1} {2}} - {\ frac {1} {2}} k ^ {2} \ operatorname {sn} \ left [{\ tfrac {2} {5}} K (k); k \ right] ^ {2} \ operatorname {sn} \ left [{\ tfrac {4} {5}} K (k); k \ right] ^ {2} = {\ frac {\ operatorname {sn} \ left [{\ frac {4} {5}} K (k); k \ right] ^ {2} - \ operatorname {sn} \ left [{\ frac {2} {5}} K ( k); k \ right] ^ {2}} {2 \ operatorname {sn} \ left [{\ frac {2} {5}} K (k); k \ right] \ operatorname {sn} \ left [{ \ frac {4} {5}} K (k); k \ direita]}}}$

Para obter os valores sn, você deve colocar a solução x nas seguintes expressões:

${\ displaystyle {\ sqrt {k ^ {2} +1}} \ operatorname {sn} \ left [{\ tfrac {2} {5}} K (k); k \ right] = {\ sqrt {2 ( -x ^ {2} -x + 1) (x ^ {2} + 1-x {\ sqrt {x ^ {2} +1}})}}}$

${\ displaystyle {\ sqrt {k ^ {2} +1}} \ operatorname {sn} \ left [{\ tfrac {4} {5}} K (k); k \ right] = {\ sqrt {2 ( -x ^ {2} -x + 1) (x ^ {2} + 1 + x {\ sqrt {x ^ {2} +1}})}}}$

Expansão em termos de nome

Deixe o Nome seja , , e deixe . Então, as funções têm expansões como a série Lambert${\ displaystyle q = \ exp (- \ pi K '(k) / K (k)) = e ^ {i \ pi \ tau}}$${\ displaystyle \ operatorname {Im} (\ tau)> 0}$${\ displaystyle m = k ^ {2}}$${\ displaystyle v = \ pi u / (2K (k))}$

${\ displaystyle \ operatorname {sn} (u; k) = {\ frac {2 \ pi} {kK (k)}} \ sum _ {n = 0} ^ {\ infty} {\ frac {q ^ {n +1/2}} {1-q ^ {2n + 1}}} \ sin ((2n + 1) v),}$

${\ displaystyle \ operatorname {cn} (u; k) = {\ frac {2 \ pi} {kK (k)}} \ sum _ {n = 0} ^ {\ infty} {\ frac {q ^ {n +1/2}} {1 + q ^ {2n + 1}}} \ cos ((2n + 1) v),}$

${\ displaystyle \ operatorname {dn} (u; k) = {\ frac {\ pi} {2K (k)}} + {\ frac {2 \ pi} {K (k)}} \ sum _ {n = 1} ^ {\ infty} {\ frac {q ^ {n}} {1 + q ^ {2n}}} \ cos (2nv)}$

quando . ${\ displaystyle q \ exp (2 | \ operatorname {Im} (v) |) <1}$

Funções elípticas de Jacobi como soluções de equações diferenciais ordinárias não lineares

Os derivados das três funções elípticas básicas de Jacobi são:

${\ displaystyle {\ frac {\ mathrm {d}} {\ mathrm {d} z}} \ operatorname {sn} (z) = \ operatorname {cn} (z) \ operatorname {dn} (z),}$

${\ displaystyle {\ frac {\ mathrm {d}} {\ mathrm {d} z}} \ operatorname {cn} (z) = - \ operatorname {sn} (z) \ operatorname {dn} (z),}$

${\ displaystyle {\ frac {\ mathrm {d}} {\ mathrm {d} z}} \ operatorname {dn} (z) = - k ^ {2} \ operatorname {sn} (z) \ operatorname {cn} (z).}$

Eles podem ser usados ​​para derivar as derivadas de todas as outras funções, conforme mostrado na tabela abaixo (argumentos (u, m) suprimidos):

Derivados ${\ displaystyle {\ frac {d} {du}} \ operatorname {pq} (u, m)}$

		q
		c	s	n	d
p
	c	0	-ds ns	-dn sn	-m 'nd sd
	s	dc nc	0	cn dn	cd nd
	n	dc sc	-cs ds	0	m cd sd
	d	m 'nc sc	-cs ns	-m cn sn	0

Com os teoremas de adição acima e para um determinado k com 0 <  k  <1, as funções principais são, portanto, soluções para as seguintes equações diferenciais ordinárias não lineares :

• ${\ displaystyle \ operatorname {sn} (x)}$resolve as equações diferenciais e${\ displaystyle {\ frac {\ mathrm {d} ^ {2} y} {\ mathrm {d} x ^ {2}}} + (1 + k ^ {2}) y-2k ^ {2} y ^ {3} = 0}$${\ displaystyle \ left ({\ frac {\ mathrm {d} y} {\ mathrm {d} x}} \ right) ^ {2} = (1-y ^ {2}) (1-k ^ {2 } y ^ {2})}$
• ${\ displaystyle \ operatorname {cn} (x)}$resolve as equações diferenciais e${\ displaystyle {\ frac {\ mathrm {d} ^ {2} y} {\ mathrm {d} x ^ {2}}} + (1-2k ^ {2}) y + 2k ^ {2} y ^ {3} = 0}$${\ displaystyle \ left ({\ frac {\ mathrm {d} y} {\ mathrm {d} x}} \ right) ^ {2} = (1-y ^ {2}) (1-k ^ {2 } + k ^ {2} y ^ {2})}$
• ${\ displaystyle \ operatorname {dn} (x)}$resolve as equações diferenciais e${\ displaystyle {\ frac {\ mathrm {d} ^ {2} y} {\ mathrm {d} x ^ {2}}} - (2-k ^ {2}) y + 2y ^ {3} = 0 }$${\ displaystyle \ left ({\ frac {\ mathrm {d} y} {\ mathrm {d} x}} \ right) ^ {2} = (y ^ {2} -1) (1-k ^ {2 } -y ^ {2})}$

Aproximação em termos de funções hiperbólicas

As funções elípticas de Jacobi podem ser expandidas em termos de funções hiperbólicas. Quando está perto da unidade, de forma que poderes superiores de podem ser negligenciados, temos: ${\ displaystyle m}$${\ displaystyle m '^ {2}}$${\ displaystyle m '}$

• sn ( u ):
  $${\ displaystyle \ operatorname {sn} (u, m) \ approx \ tanh (u) + {\ frac {1} {4}} m '(\ sinh (u) \ cosh (u) -u) \ operatorname { sech} ^ {2} (u).}$$

  
• cn ( u ):
  $${\ displaystyle \ operatorname {cn} (u, m) \ approx \ operatorname {sech} (u) - {\ frac {1} {4}} m '(\ sinh (u) \ cosh (u) -u) \ tanh (u) \ operatorname {sech} (u).}$$

  
• dn ( u ):
  $${\ displaystyle \ operatorname {dn} (u, m) \ approx \ operatorname {sech} (u) + {\ frac {1} {4}} m '(\ sinh (u) \ cosh (u) + u) \ tanh (u) \ operatorname {sech} (u).}$$

  
• am ( u ):
  $${\ displaystyle \ operatorname {am} (u, m) \ approx \ operatorname {gd} (u) + {\ frac {1} {4}} m '(\ sinh (u) \ cosh (u) -u) \ operatorname {sech} (u).}$$

  

Frações contínuas

Assumindo números reais com e o nome , com módulo elíptico . Se , onde está a integral elíptica completa do primeiro tipo , então mantém a seguinte expansão de fração contínua${\ displaystyle a, p}$${\ displaystyle 0 <a <p}$ ${\ displaystyle q = e ^ {\ pi i \ tau}}$${\ displaystyle \ operatorname {Im} (\ tau)> 0}$ ${\ textstyle k (\ tau) = {\ sqrt {1-k '(\ tau) ^ {2}}} = (\ vartheta _ {10} (0; \ tau) / \ vartheta _ {00} (0 ; \ tau)) ^ {2}}$${\ displaystyle K [\ tau] = K (k (\ tau))}$${\ displaystyle K (x) = \ pi / 2 \ cdot {} _ {2} F_ {1} (1 / 2,1 / 2; 1; x ^ {2})}$

${\ displaystyle {\ begin {alinhado} & {\ frac {{\ textrm {dn}} \ left ((p / 2-a) \ tau K \ left [{\ frac {p \ tau} {2}} \ direita]; k \ left ({\ frac {p \ tau} {2}} \ right) \ right)} {\ sqrt {k '\ left ({\ frac {p \ tau} {2}} \ right) }}} = {\ frac {\ sum _ {n = - \ infty} ^ {\ infty} q ^ {p / 2n ^ {2} + (p / 2-a) n}} {\ sum _ {n = - \ infty} ^ {\ infty} (- 1) ^ {n} q ^ {p / 2n ^ {2} + (p / 2-a) n}}} \\ [4pt] = {} & - 1 + {\ frac {2} {1 -}} {\ frac {q ^ {a} + q ^ {pa}} {1-q ^ {p} +}} {\ frac {(q ^ {a} + q ^ {2p-a}) (q ^ {a + p} + q ^ {pa})} {1-q ^ {3p} +}} {\ frac {q ^ {p} (q ^ {a } + q ^ {3p-a}) (q ^ {a + 2p} + q ^ {pa})} {1-q ^ {5p} +}} {\ frac {q ^ {2p} (q ^ { a} + q ^ {4p-a}) (q ^ {a + 3p} + q ^ {pa})} {1-q ^ {7p} +}} \ ldots \ end {alinhados}}}$