Grupo poliédrico - Polyhedral group

Grupos de pontos em três dimensões
Grupo poliédrico , [n, 3], (* n32)
Simetria involucional C _s , (*) [] =	Simetria cíclica C _nv , (* nn) [n] =	Simetria diedral D _nh , (* n22) [n, 2] =
Simetria tetraédrica T _d , (* 332) [3,3] =	Simetria octaédrica O _h , (* 432) [4,3] =	Simetria icosaédrica I _h , (* 532) [5,3] =

Em geometria , o grupo poliédrico é qualquer um dos grupos de simetria dos sólidos platônicos .

Grupos

Existem três grupos poliédricos:

O grupo tetraédrico de ordem 12, grupo de simetria rotacional do tetraedro regular . É isomórfico a A ₄ .
- As classes de conjugação
  de T são:
  - identidade
  - 4 × rotação de 120 °, ordem 3, cw
  - 4 × rotação de 120 °, ordem 3, ccw
  - 3 × rotação de 180 °, ordem 2
O grupo octaédrico de ordem 24, grupo de simetria rotacional do cubo e o octaedro regular . É isomórfico a S ₄ .
- As classes de conjugação de O são:
  - identidade
  - 6 × rotação de ± 90 ° em torno dos vértices, ordem 4
  - 8 × rotação de ± 120 ° em torno dos centros do triângulo, ordem 3
  - 3 × rotação de 180 ° em torno dos vértices, ordem 2
  - 6 × rotação de 180 ° em torno dos pontos médios das arestas, ordem 2
O grupo icosaédrico de ordem 60, grupo de simetria rotacional do dodecaedro regular e do icosaedro regular . É isomórfico a A ₅ .
- As classes de conjugação de I são:
  - identidade
  - 12 × rotação de ± 72 °, ordem 5
  - 12 × rotação de ± 144 °, ordem 5
  - 20 × rotação em ± 120 °, ordem 3
  - 15 × rotação em 180 °, ordem 2

Essas simetrias dobram para 24, 48, 120, respectivamente, para os grupos refletivos completos. As simetrias de reflexão têm 6, 9 e 15 espelhos, respectivamente. A simetria octaédrica, [4,3] pode ser vista como a união de 6 espelhos de simetria tetraédrica [3,3] e 3 espelhos de simetria diédrica Dih ₂ , [2,2]. A simetria piritoédrica é outra duplicação da simetria tetraédrica.

As classes de conjugação de simetria tetraédrica completa, T _d ≅ S ₄ , são:

identidade
8 × rotação de 120 °
3 × rotação em 180 °
6 × reflexão em um plano através de dois eixos de rotação
6 × rotorreflecção em 90 °

As classes de conjugação de simetria piritoédrica, T _h , incluem as de T , com as duas classes de 4 combinadas, e cada uma com inversão:

identidade
8 × rotação de 120 °
3 × rotação em 180 °
inversão
8 × rotorreflecção em 60 °
3 × reflexão em um plano

As classes de conjugação do grupo octaédrico completo, O _h ≅ S ₄ × C ₂ , são:

inversão
6 × rotorreflecção em 90 °
8 × rotorreflecção em 60 °
3 × reflexão em um plano perpendicular a um eixo de 4 vezes
6 × reflexão em um plano perpendicular a um eixo de 2 dobras

As classes de conjugação de simetria icosaédrica completa, I _h ≅ A ₅ × C ₂ , incluem também cada uma com inversão:

inversão
12 × rotorreflecção em 108 °, ordem 10
12 × rotorreflecção em 36 °, ordem 10
20 × rotorreflecção em 60 °, ordem 6
15 × reflexão, ordem 2

Grupos poliédricos quirais

Grupos poliédricos quirais
Nome ( orbe )	Notação de Coxeter	Pedido	Estrutura abstrata	Pontos de rotação # _valência	Diagramas
Nome ( orbe )	Notação de Coxeter	Pedido	Estrutura abstrata	Pontos de rotação # _valência	Ortogonal	Estereográfico
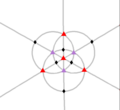
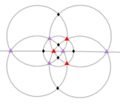
T (332)	[3,3] ⁺	12	A ₄	4 ₃ 3 ₂
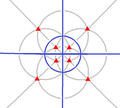
T _h (3 * 2)	[4,3 ⁺ ]	24	A ₄ × 2	4 ₃ 3 _{* 2}
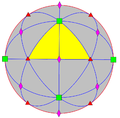
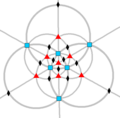
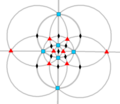
O (432)	[4,3] ⁺	24	S ₄	3 ₄ 4 ₃ 6 ₂
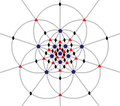
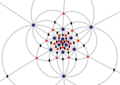
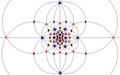
I (532)	[5,3] ⁺	60	A ₅	6 ₅ 10 ₃ 15 ₂

Grupos poliédricos completos

Grupos poliédricos completos
Weyl Schoe. ( Orbe )	Notação de Coxeter	Pedido	Estrutura abstrata	Número de Coxeter (h)	Espelhos (m)	Diagramas de espelho
Weyl Schoe. ( Orbe )	Notação de Coxeter	Pedido	Estrutura abstrata	Número de Coxeter (h)	Espelhos (m)	Ortogonal	Estereográfico
A ₃ T _d (* 332)	[3,3]	24	S ₄	4	6
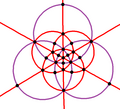
B ₃ O _h (* 432)	[4,3]	48	S ₄ × 2	8	3 6
H ₃ I _h (* 532)	[5,3]	120	A ₅ × 2	10	15