Classificação Bianchi - Bianchi classification

Em matemática , a classificação de Bianchi fornece uma lista de todas as álgebras de Lie tridimensionais reais ( até o isomorfismo ). A classificação contém 11 classes, 9 das quais contêm uma única álgebra de Lie e duas das quais contêm uma família de tamanho contínuo de álgebras de Lie. (Às vezes, dois dos grupos são incluídos nas famílias infinitas, dando 9 em vez de 11 classes.) A classificação é importante em geometria e física, porque os grupos de Lie associados servem como grupos de simetria de variedades Riemannianas tridimensionais . Seu nome é em homenagem a Luigi Bianchi , que o elaborou em 1898.

O termo "classificação de Bianchi" também é usado para classificações semelhantes em outras dimensões e para classificações de álgebras de Lie complexas .

Classificação em dimensão menor que 3

• Dimensão 0: a única álgebra de Lie é a álgebra de Lie abeliana R ⁰ .
• Dimensão 1: A única álgebra de Lie é a álgebra de Lie abeliana R ¹ , com o grupo de automorfismo externo o grupo multiplicativo de números reais diferentes de zero.
• Dimensão 2: Existem duas álgebras de Lie:
  • (1) Álgebra de Lie abeliana R ² , com grupo de automorfismo externo GL ₂ ( R ) .
  • (2) A álgebra de Lie solucionável de matrizes triangulares superiores 2 × 2 do traço 0. Ela tem um centro trivial e um grupo de automorfismo externo trivial. O grupo de Lie simplesmente conectado associado é o grupo afim da linha.

Classificação na dimensão 3

Todo o Lie 3-dimensional algebras diferente de tipos VIII e IX pode ser construído como um produto semidirect de R ² e R , com R agindo em R ² em cerca de 2 por 2 matriz M . Os diferentes tipos correspondem a diferentes tipos de matrizes M , conforme descrito a seguir.

• Tipo I : Esta é a álgebra de Lie abeliana e unimodular R ³ . O grupo simplesmente conectado possui R ³ central e grupo de automorfismo externo GL ₃ ( R ). Este é o caso quando M é 0.
• Tipo II : a álgebra de Heisenberg , que é nilpotente e unimodular. O grupo simplesmente conectado tem o centro R e o grupo de automorfismo externo GL ₂ ( R ). Este é o caso quando M é nilpotente, mas não 0 (autovalores todos 0).
• Tipo III : Esta álgebra é um produto de R e da álgebra de Lie não abeliana bidimensional. (É um caso limite do tipo VI, onde um valor próprio torna-se zero.) É solucionável e não unimodular. O grupo simplesmente conectado tem o centro R e o grupo de automorfismo externo o grupo de números reais diferentes de zero. A matriz M tem um autovalor zero e um autovalor diferente de zero.
• Tipo IV : a álgebra gerada por [ y , z ] = 0, [ x , y ] = y , [ x , z ] = y + z . É solucionável e não unimodular. O grupo simplesmente conectado tem centro trivial e grupo de automorfismo externo o produto dos reais e um grupo de ordem 2. A matriz M tem dois autovalores iguais diferentes de zero, mas não é diagonalizável .
• Digite V : [ y , z ] = 0, [ x , y ] = y , [ x , z ] = z . Solúvel e não unimodular. (Um caso limite do tipo VI onde ambos os valores próprios são iguais.) O grupo simplesmente conectado tem centro trivial e grupo de automorfismo externo os elementos de GL ₂ ( R ) do determinante +1 ou -1. A matriz M tem dois autovalores iguais e é diagonalizável.
• Tipo VI : Uma família infinita: produtos semidiretos de R ² por R , onde a matriz M tem autovalores reais distintos não zero com soma diferente de zero. As álgebras são solucionáveis ​​e não unimodulares. O grupo simplesmente conectado tem centro trivial e grupo de automorfismo externo um produto dos números reais diferentes de zero e um grupo de ordem 2.
• Tipo VI ₀ : Esta álgebra de Lie é o produto semidireto de R ² por R , com R onde a matriz M tem autovalores reais distintos diferentes de zero com soma zero. É solucionável e unimodular. É a álgebra de Lie do grupo de Poincaré bidimensional , o grupo de isometrias do espaço de Minkowski bidimensional . O grupo simplesmente conectado tem centro trivial e grupo de automorfismo externo o produto dos números reais positivos com o grupo diédrico de ordem 8.
• Tipo VII : Uma família infinita: produtos semidiretos de R ² por R , onde a matriz M possui autovalores não reais e não imaginários. Solúvel e não unimodular. O grupo simplesmente conectado tem um centro trivial e o grupo de automorfismo externo os reais diferentes de zero.
• Tipo VII ₀ : Produto semidireto de R ² por R , onde a matriz M possui autovalores imaginários diferentes de zero. Solúvel e unimodular. Esta é a álgebra de Lie do grupo de isometrias do plano. O grupo simplesmente conectado tem o centro Z e o grupo de automorfismo externo um produto dos números reais diferentes de zero e um grupo de ordem 2.
• Tipo VIII : A álgebra de Lie sl ₂ ( R ) de matrizes 2 por 2 sem rastros, associada ao grupo SL ₂ (R) . É simples e unimodular. O grupo simplesmente conectado não é um grupo de matriz; é denotado por , tem centro Z e seu grupo de automorfismo externo tem ordem 2.${\ displaystyle {\ overline {{\ mbox {SL}} (2, \ mathbf {R})}}}$
• Tipo IX : A álgebra de Lie do grupo ortogonal O ₃ ( R ). É denotado por 𝖘𝖔 (3) e é simples e unimodular. O grupo simplesmente conectado correspondente é SU (2) ; tem centro de ordem 2 e grupo de automorfismo externo trivial e é um grupo de spin .

A classificação das álgebras de Lie complexas tridimensionais é semelhante, exceto que os tipos VIII e IX se tornam isomórficos, e os tipos VI e VII se tornam parte de uma única família de álgebras de Lie.

Os grupos de Lie tridimensionais conectados podem ser classificados como segue: eles são um quociente do grupo de Lie simplesmente conectado correspondente por um subgrupo discreto do centro, portanto, podem ser lidos na tabela acima.

Os grupos estão relacionados às 8 geometrias da conjectura de geometrização de Thurston . Mais precisamente, sete das 8 geometrias podem ser realizadas como uma métrica invariante à esquerda no grupo simplesmente conectado (às vezes em mais de uma maneira). A geometria de Thurston do tipo S ² × R não pode ser realizada dessa maneira.

Constantes de estrutura

Cada um dos espaços de Bianchi tridimensionais admite um conjunto de três campos de vetores Killing que obedecem à seguinte propriedade: ${\ displaystyle \ xi _ {i} ^ {(a)}}$

${\ displaystyle \ left ({\ frac {\ partial \ xi _ {i} ^ {(c)}} {\ partial x ^ {k}}} - {\ frac {\ partial \ xi _ {k} ^ { (c)}} {\ parcial x ^ {i}}} \ direita) \ xi _ {(a)} ^ {i} \ xi _ {(b)} ^ {k} = C _ {\ ab} ^ { c}}$

onde , as "constantes de estrutura" do grupo, formam um tensor antissimétrico de ordem três constante em seus dois índices inferiores. Para qualquer espaço Bianchi tridimensional, é dado pela relação ${\ displaystyle C _ {\ ab} ^ {c}}$ ${\ displaystyle C _ {\ ab} ^ {c}}$

${\ displaystyle C _ {\ ab} ^ {c} = \ varepsilon _ {abd} n ^ {cd} - \ delta _ {a} ^ {c} a_ {b} + \ delta _ {b} ^ {c} a_ {a}}$

onde é o símbolo de Levi-Civita , é o delta de Kronecker , e o vetor e o tensor diagonal são descritos pela tabela a seguir, onde dá o i- ésimo autovalor de ; o parâmetro a passa por todos os números reais positivos : ${\ displaystyle \ varepsilon _ {abd}}$${\ displaystyle \ delta _ {a} ^ {c}}$${\ displaystyle a_ {a} = (a, 0,0)}$${\ displaystyle n ^ {cd}}$${\ displaystyle n ^ {(i)}}$${\ displaystyle n ^ {cd}}$

Tipo Bianchi	${\ displaystyle a}$	${\ displaystyle n ^ {(1)}}$	${\ displaystyle n ^ {(2)}}$	${\ displaystyle n ^ {(3)}}$	aula	notas	gráfico (Fig. 1)
eu	0	0	0	0	UMA	descreve o espaço euclidiano	na origem
II	0	1	0	0	UMA		intervalo [0,1] ao longo ${\ displaystyle n ^ {(1)}}$
III	1	0	1	-1	B	o subcaso do tipo VI a com${\ displaystyle a = 1}$	projeta para o quarto quadrante do plano a = 0
4	1	0	0	1	B		face aberta vertical entre o primeiro e o quarto quadrantes do plano a = 0
V	1	0	0	0	B	tem uma hiper- pseudoesfera como um caso especial	o intervalo (0,1] ao longo do eixo a
VI 0	0	1	-1	0	UMA		quarto quadrante do plano horizontal
VI a	${\ displaystyle a}$	0	1	-1	B	quando , equivalente ao tipo III${\ displaystyle a = 1}$	projeta para o quarto quadrante do plano a = 0
VII 0	0	1	1	0	UMA	tem o espaço euclidiano como um caso especial	primeiro quadrante do plano horizontal
VII a	${\ displaystyle a}$	0	1	1	B	tem uma hiper-pseudosfera como um caso especial	projeta para o primeiro quadrante do plano a = 0
VIII	0	1	1	-1	UMA		sexto outubro
IX	0	1	1	1	UMA	tem uma hiperesfera como um caso especial	segundo octante

Figura 1. O espaço de parâmetro como um plano 3 (classe A) e um meio plano ortogonal 3 (classe B) em R ⁴ com coordenadas ( n ⁽¹⁾ , n ⁽²⁾ , n ⁽³⁾ , a ), mostrando os representantes canônicos de cada tipo de Bianchi.

A classificação Bianchi padrão pode ser derivada das constantes estruturais nas seguintes seis etapas:

1. Devido à antissimetria , existem nove constantes independentes . Estes podem ser representados de forma equivalente pelos nove componentes de uma matriz constante arbitrária C ^ab : onde ε _abd é o símbolo tridimensional de Levi-Civita totalmente antissimétrico (ε ₁₂₃ = 1). Substituição desta expressão para na identidade de Jacobi , resulta em${\ displaystyle C_ {ab} ^ {c} = - C_ {ba} ^ {c}}$${\ displaystyle C_ {ab} ^ {c}}$
   ${\ displaystyle C_ {ab} ^ {c} = \ varepsilon _ {abd} C ^ {dc},}$
   ${\ displaystyle C_ {ab} ^ {c}}$
   ${\ displaystyle \ varepsilon _ {abd} C ^ {bd} C ^ {ac} = 0.}$
2. As constantes de estrutura podem ser transformadas como: O aparecimento de det A nesta fórmula é devido ao fato de que o símbolo ε _{abd se} transforma em densidade tensorial :, onde έ _mnd ≡ ε _mnd . Por meio dessa transformação é sempre possível reduzir a matriz C ^ab à forma: Após tal escolha, ainda se tem a liberdade de fazer transformações em tríades, mas com as restrições e
   ${\ displaystyle C ^ {ab} = \ left (\ det {A} \ right) ^ {- 1} A_ {m} ^ {a} A_ {n} ^ {b} {\ agudo {C}} ^ { mn}.}$
   ${\ displaystyle \ varepsilon _ {abc} = \ left (\ det {A} \ right) D_ {a} ^ {m} D_ {b} ^ {n} D_ {c} ^ {d} {\ agudo {\ varejpsilon}} _ {mnd}}$
   ${\ displaystyle C ^ {ab} = {\ begin {bmatrix} n_ {1} & 0 & 0 \\ 0 & C ^ {22} & C ^ {23} \\ 0 & C ^ {32} & C ^ {33} \ end {bmatrix}} .}$
   ${\ displaystyle A_ {2} ^ {1} = A_ {3} ^ {1} = 0}$${\ displaystyle A_ {1} ^ {2} = A_ {1} ^ {3} = 0.}$
3. Agora, as identidades Jacobi fornecem apenas uma restrição:
   ${\ displaystyle \ left (C ^ {23} -C ^ {32} \ right) n_ {1} = 0.}$
4. Se n ₁ ≠ 0 então C ²³ - C ³² = 0 e pelas transformações restantes com , a matriz 2 × 2 em C ^ab pode ser tornada diagonal. Então, a condição de diagonalidade para C ^ab é preservada sob as transformações com diagonal . Sob essas transformações, os três parâmetros n ₁ , n ₂ , n ₃ mudam da seguinte maneira: Por essas transformações diagonais, o módulo de qualquer n _a (se não for zero) pode ser igualado à unidade. Levando em consideração que a mudança simultânea de sinal de todos os n _a não produz nada de novo, chega-se aos seguintes conjuntos invariantemente diferentes para os números n ₁ , n ₂ , n ₃ (invariantemente diferente no sentido de que não há como passar de um para o outro por alguma transformação da tríade ), ou seja, para os seguintes tipos diferentes de espaços homogêneos com matriz diagonal C ^ab :${\ displaystyle A _ {\ bar {b}} ^ {\ bar {a}} \ neq 0, \ quad {\ bar {a}}, {\ bar {b}} = {\ bar {2}}, { \ bar {3}}}$${\ displaystyle C ^ {{\ bar {a}} {\ bar {b}}}}$
   ${\ displaystyle C ^ {ab} = {\ begin {bmatrix} n_ {1} & 0 & 0 \\ 0 & n_ {2} & 0 \\ 0 & 0 & n_ {3} \ end {bmatrix}}.}$
   ${\ displaystyle A_ {b} ^ {a}}$
   ${\ displaystyle n_ {a} = \ left (A_ {1} ^ {1} A_ {2} ^ {2} A_ {3} ^ {3} \ right) \ left (A_ {a} ^ {a} \ direita) ^ {2} {\ agudo {n}} _ {a}, {\ text {sem soma sobre}} \ a.}$
   ${\ displaystyle e_ {a} ^ {\ bar {a}} = A _ {\ bar {b}} ^ {\ bar {a}} e_ {a} ^ {\ bar {b}}}$
   ${\ displaystyle {\ begin {matrix} Bianchi \ IX &: & (n_ {1}, n_ {2}, n_ {3}) & = & (1,1,1), \\ Bianchi \ VIII &: & (n_ {1}, n_ {2}, n_ {3}) & = & (1,1, -1), \\ Bianchi \ VII_ {0} &: & (n_ {1}, n_ {2}, n_ { 3}) & = & (1,1,0), \\ Bianchi \ VI_ {0} &: & (n_ {1}, n_ {2}, n_ {3}) & = & (1, -1, 0), \\ Bianchi \ II &: & (n_ {1}, n_ {2}, n_ {3}) & = & (1,0,0). \ End {matriz}}}$
5. Considere agora o caso n ₁ = 0. Também pode acontecer nesse caso que C ²³ - C ³² = 0. Isso retorna à situação já analisada na etapa anterior, mas com a condição adicional n ₁ = 0. Agora, todos essencialmente tipos diferentes para os conjuntos n ₁ , n ₂ , n ₃ são (0, 1, 1), (0, 1, −1), (0, 0, 1) e (0, 0, 0). Os três primeiros repetem os tipos VII ₀ , VI ₀ , II . Consequentemente, apenas um novo tipo surge:
   ${\ displaystyle Bianchi \ I \: \ (n_ {1}, n_ {2}, n_ {3}) \ = \ (0,0,0).}$
6. O único caso restante é n ₁ = 0 e C ²³ - C ³² ≠ 0. Agora, a matriz 2 × 2 é não simétrica e não pode ser diagonal por transformações usando . Porém, sua parte simétrica pode ser diagonalizada, ou seja, a matriz 3 × 3 C ^ab pode ser reduzida à forma: onde a é um número arbitrário. Depois de feito isso, ainda resta a possibilidade de realizar transformações com diagonal , sob as quais as quantidades n ₂ , n ₃ e uma alteração da seguinte forma: Essas fórmulas mostram que para n ₂ , n ₃ , a diferente de zero , a combinação a ² ( n ₂ n ₃ ) ⁻¹ é uma quantidade invariante. Por uma escolha de , pode-se impor a condição a > 0 e após isso ser feito, a escolha do sinal de permite alterar ambos os sinais de n ₂ e n ₃ simultaneamente, ou seja, o conjunto ( n ₂ , n ₃ ) é equivalente ao conjunto (- n ₂ , - n ₃ ). Segue-se que existem as seguintes quatro possibilidades diferentes: Para as duas primeiras, o número a pode ser transformado em unidade por uma escolha dos parâmetros e . Para as duas segundas possibilidades, ambos os parâmetros já estão fixos e a permanece um número positivo invariante e arbitrário. Historicamente, esses quatro tipos de espaços homogêneos foram classificados como: Tipo III é apenas um caso particular do tipo VI correspondendo a a = 1. Os tipos VII e VI contêm uma infinidade de tipos invariantemente diferentes de álgebras correspondentes à arbitrariedade do parâmetro contínuo a . O tipo VII ₀ é um caso particular de VII correspondendo a a = 0 enquanto o tipo VI ₀ é um caso particular de VI correspondendo também a a = 0.${\ displaystyle C ^ {{\ bar {a}} {\ bar {b}}} ({\ bar {a}}, {\ bar {b}} = 2,3)}$${\ displaystyle A _ {\ bar {b}} ^ {\ bar {a}} \ neq 0}$
   ${\ displaystyle C ^ {ab} = {\ begin {bmatrix} 0 & 0 & 0 \\ 0 & n_ {2} & a \\ 0 & -a & n_ {3} \ end {bmatrix}},}$
   ${\ displaystyle A _ {\ bar {b}} ^ {\ bar {a}}}$
   ${\ displaystyle n_ {2} = \ left (A_ {1} ^ {1} A_ {2} ^ {2} A_ {3} ^ {3} \ right) ^ {- 1} \ left (A_ {2} ^ {2} \ right) ^ {2} {\ sharp {n}} _ {2}, \ quad n_ {3} = \ left (A_ {1} ^ {1} A_ {2} ^ {2} A_ {3} ^ {3} \ right) ^ {- 1} \ left (A_ {3} ^ {3} \ right) ^ {2} {\ agudo {n}} _ {3}, \ quad a = \ esquerda (A_ {1} ^ {1} \ direita) ^ {- 1} {\ agudo {a}}.}$
   ${\ displaystyle A_ {1} ^ {1}}$${\ displaystyle A_ {3} ^ {3} \ left (A_ {2} ^ {2} \ right) ^ {- 1}}$
   ${\ displaystyle (a, n_ {2}, n_ {3}) = (a, 0,0), (a, 0,1), (a, 1,1), (a, 1, -1). }$
   
   ${\ displaystyle A_ {1} ^ {1}}$${\ displaystyle A_ {3} ^ {3} \ left (A_ {2} ^ {2} \ right) ^ {- 1}}$
   ${\ displaystyle {\ begin {matrix} Bianchi \ V &: & n_ {1} = 0, \ (a, n_ {2}, n_ {3}) & = & (1,0,0), \\ Bianchi \ IV & : & n_ {1} = 0, \ (a, n_ {2}, n_ {3}) & = & (1,0,1), \\ Bianchi \ VII &: & n_ {1} = 0, \ (a, n_ {2}, n_ {3}) & = & (a, 1,1), \\ Bianchi \ III &: & n_ {1} = 0, \ (a, n_ {2}, n_ {3}) & = & (1,1, -1), \\ Bianchi \ VI &: & n_ {1} = 0, \ (a, n_ {2}, n_ {3}) & = & (a, 1, -1). \ fim {matriz}}}$
   

Curvatura dos espaços Bianchi

Os espaços de Bianchi têm a propriedade de que seus tensores de Ricci podem ser separados em um produto dos vetores de base associados ao espaço e um tensor independente de coordenadas.

Para uma determinada métrica :

${\ displaystyle ds ^ {2} = \ gamma _ {ab} \ xi _ {i} ^ {(a)} \ xi _ {k} ^ {(b)} dx ^ {i} dx ^ {k}}$

(onde 　são formas 1 ), o tensor de curvatura de Ricci é dado por: ${\ displaystyle \ xi _ {i} ^ {(a)} dx ^ {i}}$${\ displaystyle R_ {ik}}$

${\ displaystyle R_ {ik} = R _ {(a) (b)} \ xi _ {i} ^ {(a)} \ xi _ {k} ^ {(b)}}$

${\ displaystyle R _ {(a) (b)} = {\ frac {1} {2}} \ left [C _ {\ \ b} ^ {cd} \ left (C_ {cda} + C_ {dca} \ right ) + C _ {\ cd} ^ {c} \ left (C_ {ab} ^ {\ \ d} + C_ {ba} ^ {\ \ d} \ right) - {\ frac {1} {2}} C_ {b} ^ {\ cd} C_ {acd} \ right]}$

onde os índices nas constantes de estrutura são aumentados e diminuídos com o que não é uma função de . ${\ displaystyle \ gamma _ {ab}}$${\ displaystyle x ^ {i}}$

Aplicação cosmológica

Em cosmologia , esta classificação é usada para um espaço-tempo homogêneo de dimensão 3 + 1. O grupo de Lie tridimensional é o grupo de simetria da fatia espacial tridimensional, e a métrica de Lorentz que satisfaz a equação de Einstein é gerada pela variação dos componentes métricos em função de t. As métricas de Friedmann-Lemaître-Robertson-Walker são isotrópicas, que são casos particulares dos tipos I, V e IX. Os modelos Bianchi tipo I incluem a métrica Kasner como um caso especial. As cosmologias Bianchi IX incluem a métrica Taub . No entanto, a dinâmica próxima à singularidade é aproximadamente governada por uma série de períodos Kasner (Bianchi I) sucessivos. A dinâmica complicada, que essencialmente equivale ao movimento do bilhar em uma parte do espaço hiperbólico, exibe um comportamento caótico e é chamada de Mixmaster ; sua análise é chamada de análise BKL em homenagem a Belinskii, Khalatnikov e Lifshitz. Trabalhos mais recentes estabeleceram uma relação de teorias de (super) gravitação perto de uma singularidade espacial (limite BKL) com álgebras de Kac-Moody de Lorentzian , grupos de Weyl e grupos de Coxeter hiperbólicos . Outro trabalho mais recente está preocupado com a natureza discreta do mapa de Kasner e uma generalização contínua. Em um espaço homogêneo e isotrópico, a métrica é determinada completamente, deixando livre apenas o sinal da curvatura. Assumindo apenas a homogeneidade do espaço, sem simetria adicional, como a isotropia, deixa consideravelmente mais liberdade na escolha da métrica. O seguinte se refere à parte espacial da métrica em um dado instante de tempo t, assumindo um quadro síncrono de modo que t seja o mesmo tempo sincronizado para todo o espaço. ${\ displaystyle \ scriptstyle {\ text {VII}} _ {h}}$

A homogeneidade implica propriedades métricas idênticas em todos os pontos do espaço. Uma definição exata deste conceito envolve a consideração de conjuntos de transformações de coordenadas que transformam o espaço em si mesmo, ou seja, deixam sua métrica inalterada: se o elemento de linha antes da transformação for

${\ displaystyle dl ^ {2} = \ gamma _ {\ alpha \ beta} \ left (x ^ {1}, x ^ {2}, x ^ {3} \ right) dx ^ {\ alpha} dx ^ { \ beta},}$

então, após a transformação, o mesmo elemento de linha é

${\ displaystyle dl ^ {2} = \ gamma _ {\ alpha \ beta} \ left (x ^ {\ prime 1}, x ^ {\ prime 2}, x ^ {\ prime 3} \ right) dx ^ { \ prime \ alpha} dx ^ {\ prime \ beta},}$

com a mesma dependência funcional de γ _αβ nas novas coordenadas. (Para uma definição mais teórica e independente de coordenadas de espaço homogêneo, consulte espaço homogêneo ). Um espaço é homogêneo se admite um conjunto de transformações ( um grupo de movimentos ) que traz qualquer ponto dado à posição de qualquer outro ponto. Como o espaço é tridimensional, as diferentes transformações do grupo são rotuladas por três parâmetros independentes.

Figura 2. A tríade e ^{( a )} ( e ⁽¹⁾ , e ⁽²⁾ , e ⁽³⁾ ) é um sistema de coordenadas afim (incluindo como um caso especial sistema de coordenadas cartesianas) cujas coordenadas são funções das coordenadas curvilíneas x _α (x ₁ , x ₂ , x ₃ ).

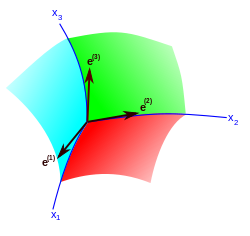
No espaço euclidiano, a homogeneidade do espaço é expressa pela invariância da métrica sob deslocamentos paralelos ( translações ) do sistema de coordenadas cartesiano . Cada translação é determinada por três parâmetros - os componentes do vetor de deslocamento da origem das coordenadas. Todas essas transformações deixam invariáveis ​​as três diferenciais independentes ( dx , dy , dz ) a partir das quais o elemento de linha é construído. No caso geral de um espaço homogêneo não euclidiano, as transformações de seu grupo de movimentos deixam novamente três formas diferenciais lineares invariantes , que não se reduzem, entretanto, a diferenciais totais de quaisquer funções de coordenadas. Essas formas são escritas como onde o índice latino ( a ) rotula três vetores independentes (funções de coordenadas); esses vetores são chamados de campo de quadro ou tríade. As letras gregas rotulam as três coordenadas curvilíneas semelhantes a espaços . Uma invariante métrica espacial é construída sob o determinado grupo de movimentos com o uso das formas acima: ${\ displaystyle e _ {\ alpha} ^ {(a)} dx ^ {\ alpha}}$

${\ displaystyle dl ^ {2} = \ eta _ {ab} \ left (e _ {\ alpha} ^ {(a)} dx ^ {\ alpha} \ right) \ left (e _ {\ beta} ^ {(b )} dx ^ {\ beta} \ right)}$

( eq. 6a )

ou seja, o tensor métrico é

${\ displaystyle \ gamma _ {\ alpha \ beta} = \ eta _ {ab} e _ {\ alpha} ^ {(a)} e _ {\ beta} ^ {(b)}}$

( eq. 6b )

onde os coeficientes η _ab , que são simétricos nos índices a e b , são funções do tempo. A escolha dos vetores de base é ditada pelas propriedades de simetria do espaço e, em geral, esses vetores de base não são ortogonais (de forma que a matriz η _ab não é diagonal).

O triplo recíproco de vetores é introduzido com a ajuda do delta de Kronecker${\ displaystyle e _ {(a)} ^ {\ alpha}}$

${\ displaystyle e _ {(a)} ^ {\ alpha} e _ {\ alpha} ^ {(b)} = \ delta _ {a} ^ {b}; \ quad e _ {(a)} ^ {\ alpha} e _ {\ beta} ^ {(a)} = \ delta _ {\ alpha} ^ {\ beta}}$

( eq. 6c )

No caso tridimensional, a relação entre os dois triplos vetoriais pode ser escrita explicitamente

${\ displaystyle \ mathbf {e} _ {(1)} = {\ frac {1} {v}} \ mathbf {e} ^ {(2)} \ times \ mathbf {e} ^ {(3)}, \ quad \ mathbf {e} _ {(2)} = {\ frac {1} {v}} \ mathbf {e} ^ {(3)} \ times \ mathbf {e} ^ {(1)}, \ quad \ mathbf {e} _ {(3)} = {\ frac {1} {v}} \ mathbf {e} ^ {(1)} \ times \ mathbf {e} ^ {(2)},}$

( eq. 6d )

onde o volume v está

${\ displaystyle v = \ left \ vert e _ {\ alpha} ^ {(a)} \ right \ vert = \ mathbf {e} ^ {(1)} \ cdot \ mathbf {e} ^ {(2)} \ vezes \ mathbf {e} ^ {(3)},}$

com e _{( um )} e de e ^{( um )} considerado como vectores cartesianas com os componentes e , respectivamente. O determinante do tensor métrico eq. 6b é γ = η v ^2, onde η é o determinante da matriz η _ab . ${\ displaystyle e _ {(a)} ^ {\ alpha}}$${\ displaystyle e _ {\ alpha} ^ {(a)}}$

As condições necessárias para a homogeneidade do espaço são

${\ displaystyle \ left ({\ frac {\ partial e _ {\ alpha} ^ {(c)}} {\ partial x ^ {\ beta}}} - {\ frac {\ partial e _ {\ beta} ^ {( c)}} {\ parcial x ^ {\ alpha}}} \ right) e _ {(a)} ^ {\ alpha} e _ {(b)} ^ {\ beta} = C_ {ab} ^ {c}. }$

( eq. 6e )

As constantes são chamadas de constantes de estrutura do grupo. ${\ displaystyle C_ {ab} ^ {c}}$

Prova da eq. 6e

A invariância das formas diferenciais significa que ${\ displaystyle e _ {\ alpha} ^ {(a)} dx ^ {\ alpha}}$ ${\ displaystyle e _ {\ alpha} ^ {(a)} (x) dx ^ {\ alpha} = e _ {\ alpha} ^ {(a)} (x ^ {\ prime}) dx ^ {\ prime \ alpha }}$ onde os nos dois lados da equação são as mesmas funções das coordenadas antigas e novas, respectivamente. Multiplicando esta equação por , definindo e comparando coeficientes das mesmas diferenciais dx α , encontra-se ${\ displaystyle e _ {\ alpha} ^ {(a)}}$${\ displaystyle e _ {(a)} ^ {\ beta} (x ^ {\ prime})}$${\ displaystyle dx ^ {\ prime \ beta} = {\ frac {\ partial x ^ {\ prime \ beta}} {\ partial x ^ {\ alpha}}} dx ^ {\ alpha},}$ ${\ displaystyle {\ frac {\ partial x ^ {\ prime \ beta}} {\ partial x ^ {\ alpha}}} = e _ {(a)} ^ {\ beta} (x ^ {\ prime}) e_ {\ alpha} ^ {(a)} (x).}$ Essas equações são um sistema de equações diferenciais que determinam as funções para um determinado quadro. Para serem integráveis, essas equações devem satisfazer de forma idêntica as condições ${\ displaystyle x ^ {\ prime \ beta} (x)}$ ${\ displaystyle {\ frac {\ partial ^ {2} x ^ {\ prime \ beta}} {\ partial x ^ {\ alpha} \ partial x ^ {\ gamma}}} = {\ frac {\ partial ^ { 2} x ^ {\ prime \ beta}} {\ partial x ^ {\ gamma} \ partial x ^ {\ alpha}}}.}$ Calculando as derivadas, encontra-se ${\ displaystyle \ left [{\ frac {\ partial e _ {(a)} ^ {\ beta} (x ^ {\ prime})} {\ partial x ^ {\ prime \ delta}}} e _ {(b) } ^ {\ delta} (x ^ {\ prime}) - {\ frac {\ partial e _ {(b)} ^ {\ beta} (x ^ {\ prime})} {\ partial x ^ {\ prime \ delta}}} e _ {(a)} ^ {\ delta} (x ^ {\ prime}) \ right] e _ {\ gamma} ^ {(b)} (x) e _ {\ alpha} ^ {(a) } (x) = e _ {(a)} ^ {\ beta} (x ^ {\ prime}) \ left [{\ frac {\ partial e _ {\ gamma} ^ {(a)} (x)} {\ parcial x ^ {\ alpha}}} - {\ frac {\ partial e _ {\ alpha} ^ {(a)} (x)} {\ partial x ^ {\ gamma}}} \ right].}$ Multiplicando ambos os lados das equações e mudando a diferenciação de um fator para outro usando a eq. 6c , obtém-se para o lado esquerdo: ${\ displaystyle e _ {(d)} ^ {\ alpha} (x) e _ {(c)} ^ {\ gamma} (x) e _ {\ beta} ^ {(f)} (x ^ {\ prime}) }$ ${\ displaystyle e _ {\ beta} ^ {(f)} (x ^ {\ prime}) \ left [{\ frac {\ partial e _ {(d)} ^ {\ beta} (x ^ {\ prime}) } {\ partial x ^ {\ prime \ delta}}} e _ {(c)} ^ {\ delta} (x ^ {\ prime}) - {\ frac {\ partial e _ {(c)} ^ {\ beta } (x ^ {\ primo})} {\ parcial x ^ {\ primo \ delta}}} e _ {(d)} ^ {\ delta} (x ^ {\ primo}) \ direita] = e _ {(c )} ^ {\ beta} (x ^ {\ prime}) e _ {(d)} ^ {\ delta} (x ^ {\ prime}) \ left [{\ frac {\ partial e _ {\ beta} ^ { (f)} (x ^ {\ primo})} {\ parcial x ^ {\ primo \ delta}}} - {\ frac {\ parcial e _ {\ delta} ^ {(f)} (x ^ {\ primo })} {\ partial x ^ {\ prime \ beta}}} \ right].}$ e para a direita, a mesma expressão na variável x . Como x e x ' são arbitrários, essas expressões devem ser reduzidas a constantes para obter a eq. 6e .

Multiplicando por , eq. 6e pode ser reescrito na forma ${\ displaystyle e _ {(c)} ^ {\ gamma}}$

${\ displaystyle e _ {(a)} ^ {\ alpha} {\ frac {\ partial e _ {(b)} ^ {\ gamma}} {\ partial x ^ {\ alpha}}} - e _ {(b)} ^ {\ beta} {\ frac {\ partial e _ {(a)} ^ {\ gamma}} {\ partial x ^ {\ beta}}} = C_ {ab} ^ {c} e _ {(c)} ^ {\ gamma}.}$

( eq. 6f )

A Equação 6e pode ser escrita em uma forma vetorial como

${\ displaystyle \ mathbf {e} _ {(a)} \ times \ mathbf {e} _ {(b)} {\ text {curl}} \ mathbf {e} ^ {(c)} = - C_ {ab } ^ {c},}$

onde novamente as operações vetoriais são feitas como se as coordenadas x ^α fossem cartesianas. Usando a eq. 6d , obtém-se

${\ displaystyle {\ frac {1} {v}} \ left (\ mathbf {e} ^ {(1)} {\ text {curl}} \ mathbf {e} ^ {(1)} \ right) = C_ {32} ^ {1}, \ quad {\ frac {1} {v}} \ left (\ mathbf {e} ^ {(2)} {\ text {curl}} \ mathbf {e} ^ {(1 )} \ right) = C_ {13} ^ {1}, \ quad {\ frac {1} {v}} \ left (\ mathbf {e} ^ {(3)} {\ text {curl}} \ mathbf {e} ^ {(1)} \ direita) = C_ {21} ^ {1}}$

( eq. 6g )

e mais seis equações obtidas por uma permutação cíclica dos índices 1, 2, 3.

As constantes de estrutura são antissimétricas em seus índices inferiores, conforme visto em sua definição eq. 6e : . Outra condição nas constantes de estrutura pode ser obtida observando que a eq. 6f pode ser escrito na forma de relações de comutação${\ displaystyle C_ {ab} ^ {c} = - C_ {ba} ^ {c}}$

${\ displaystyle \ left [X_ {a}, X_ {b} \ right] \ equiv X_ {a} X_ {b} -X_ {b} X_ {a} = C_ {ab} ^ {c} X_ {c} }$

( eq. 6h )

para os operadores diferenciais lineares

${\ displaystyle X_ {a} = e _ {(a)} ^ {\ alpha} {\ frac {\ partial} {\ partial x ^ {\ alpha}}}}$

( eq. 6i )

Na teoria matemática de grupos contínuos ( grupos de Lie ), os operadores X _a condições satisfatórias eq. 6h são chamados de geradores do grupo . A teoria dos grupos de Lie usa operadores definidos usando os vetores Killing em vez de tríades . Como na métrica síncrona nenhum dos componentes γ _αβ depende do tempo, os vetores de Killing (tríades) são semelhantes ao tempo. ${\ displaystyle \ xi _ {(a)} ^ {\ alpha}}$${\ displaystyle e _ {(a)} ^ {\ alpha}}$

As condições eq. 6h seguem da identidade Jacobi

${\ displaystyle [[X_ {a}, X_ {b}], X_ {c}] + [[X_ {b}, X_ {c}], X_ {a}] + [[X_ {c}, X_ { a}], X_ {b}] = 0}$

e tem o formulário

${\ displaystyle C_ {ab} ^ {e} C_ {ec} ^ {d} + C_ {bc} ^ {e} C_ {ea} ^ {d} + C_ {ca} ^ {e} C_ {eb} ^ {d} = 0}$

( eq. 6j )

É uma vantagem definitiva usar, no lugar das constantes de três índices , um conjunto de quantidades de dois índices, obtido pela transformação dual ${\ displaystyle C_ {ab} ^ {c}}$

${\ displaystyle C_ {ab} ^ {c} = e_ {abd} C ^ {dc}}$

( eq. 6k )

onde e _abc = e ^abc é o símbolo anti-simétrico da unidade (com e ₁₂₃ = +1). Com essas constantes, as relações de comutação eq. 6h são escritas como

${\ displaystyle e ^ {abc} X_ {b} X_ {c} = C ^ {ad} X_ {d}}$

( eq. 6l )

A propriedade de antissimetria já foi levada em consideração na definição eq. 6k , enquanto a propriedade eq. 6j assume a forma

${\ displaystyle e_ {bcd} C ^ {cd} C ^ {ba} = 0}$

( eq. 6m )

A escolha dos três vetores de quadro nas formas diferenciais (e com eles os operadores X _a ) não é única. Eles podem ser submetidos a qualquer transformação linear com coeficientes constantes: ${\ displaystyle e _ {\ alpha} ^ {(a)} dx ^ {\ alpha}}$

${\ displaystyle \ mathbf {e} _ {(a)} = A_ {a} ^ {b} \ mathbf {e} _ {(b)}.}$

( eq. 6n )

As quantidades η _ab e C ^ab comportam-se como tensores (são invariantes) em relação a tais transformações.

As condições eq. 6m são os únicos que as constantes de estrutura devem satisfazer. Mas entre as constantes admissíveis por essas condições, existem conjuntos equivalentes, no sentido de que sua diferença está relacionada a uma transformação do tipo eq. 6n . A questão da classificação de espaços homogêneos se reduz à determinação de todos os conjuntos não equivalentes de constantes de estrutura. Isso pode ser feito, usando as propriedades de "tensor" das quantidades C ^ab , pelo seguinte método simples (CG Behr, 1962).

O tensor assimétrico C ^ab pode ser resolvido em uma parte simétrica e uma parte antissimétrica. O primeiro é denotado por n ^ab , e o segundo é expresso em termos de seu vetor dual a _c :

${\ displaystyle C ^ {ab} = n ^ {ab} + e ^ {abc} a_ {c}.}$

( eq. 6o )

Substituição desta expressão na eq. 6m leva à condição

${\ displaystyle n ^ {ab} a_ {b} = 0.}$

( eq. 6p )

Por meio das transformações eq. 6n o tensor simétrico n ^ab pode ser levado à forma diagonal com autovalores n ₁ , n ₂ , n ₃ . A Equação 6p mostra que o vetor a _b (se existir) encontra-se ao longo de uma das direções principais do tensor n ^ab , aquela que corresponde ao valor próprio zero. Sem perda de generalidade, pode-se, portanto, definir a _b = ( a , 0, 0). Então eq. 6p reduz-se a um ₁ = 0, isto é uma das quantidades de um ou n ₁ deve ser zero. As identidades Jacobi assumem a forma:

${\ displaystyle [X_ {1}, X_ {2}] = - aX_ {2} + n_ {3} X_ {3}, \ quad [X_ {2}, X_ {3}] = n_ {1} X_ { 1}, \ quad [X_ {3}, X_ {1}] = n_ {2} X_ {2} + aX_ {3}.}$

( eq. 6q )

As únicas liberdades restantes são as mudanças de sinal dos operadores X _a e sua multiplicação por constantes arbitrárias. Isto permite ao mesmo tempo mudar o sinal de todos os n _um e também para fazer a quantidade de positivo (se for diferente de zero). Além disso, todas as constantes de estrutura podem ser igualadas a ± 1, se pelo menos uma das quantidades a , n ₂ , n ₃ desaparecer. Mas se todas essas três quantidades diferem de zero, as transformações de escala deixam invariante a razão h = a ² ( n ₂ n ₃ ) ^-1 .

Assim, chega-se à classificação de Bianchi listando os possíveis tipos de espaços homogêneos classificados pelos valores de a , n ₁ , n ₂ , n ₃ que é apresentado graficamente na Fig. 3. No caso da classe A ( a = 0), digite IX ( n ⁽¹⁾ = 1, n ⁽²⁾ = 1, n ⁽³⁾ = 1) é representado pelo octante 2, tipo VIII ( n ⁽¹⁾ = 1, n ⁽²⁾ = 1, n ⁽³⁾ = –1) é representado pelo octante 6, enquanto o tipo VII ₀ ( n ⁽¹⁾ = 1, n ⁽²⁾ = 1, n ⁽³⁾ = 0) é representado pelo primeiro quadrante do plano horizontal e o tipo VI ₀ ( n ⁽¹⁾ = 1, n ⁽²⁾ = –1, n ⁽³⁾ = 0) é representado pelo quarto quadrante deste plano; tipo II (( n ⁽¹⁾ = 1, n ⁽²⁾ = 0, n ⁽³⁾ = 0) é representado pelo intervalo [0,1] ao longo de n ⁽¹⁾ e tipo I ( n ⁽¹⁾ = 0 , n ⁽²⁾ = 0, n ⁽³⁾ = 0) está na origem. Da mesma forma, no caso da classe B (com n ⁽³⁾ = 0), Bianchi tipo VI _h ( a = h , n ⁽¹⁾ = 1, n ⁽²⁾ = -1) projeta para o quarto quadrante do plano horizontal e tipo VII _h ( a = h , n ⁽¹⁾ = 1, n ⁽²⁾ = 1) projeta para o primeiro quadrante do plano horizontal plano; estes dois últimos tipos são uma única classe de isomorfismo correspondendo a uma superfície de valor constante da função h = a ² ( n ⁽¹⁾ n ⁽²⁾ ) ^-1 . Uma superfície típica é ilustrada em um octante, o ângulo θ dado por tan  θ = | h / 2 | ^1/2 ; aqueles nos octantes restantes são obtidos por rotação através de múltiplos de π / 2, h alternando no sinal para uma dada magnitude | h |. O tipo III é um subtipo de VI _h com um = 1. tipo V ( um = 1, n ⁽¹⁾ = 0, N ⁽²⁾ = 0) é o intervalo (0,1] ao longo do eixo de um e do tipo IV ( um = 1, N ⁽¹⁾ = 1, n ⁽²⁾ = 0) é a face aberta vertical entre o primeiro e o quarto quadrantes do plano a = 0 com o último dando o limite de classe A de cada tipo.

As equações de Einstein para um universo com um espaço homogêneo podem ser reduzidas a um sistema de equações diferenciais ordinárias contendo apenas funções de tempo com a ajuda de um campo de moldura. Para fazer isso, deve-se resolver os componentes espaciais de quatro vetores e quatro tensores ao longo da tríade de vetores de base do espaço:

${\ displaystyle R _ {(a) (b)} = R _ {\ alpha \ beta} e _ {(a)} ^ {\ alpha} e _ {(b)} ^ {\ beta}, \ quad R_ {0 (a )} = R_ {0 \ alpha} e _ {(a)} ^ {\ alpha}, \ quad u ^ {(a)} = u ^ {\ alpha} e _ {\ alpha} ^ {(a)},}$

onde todas essas quantidades são agora funções apenas de t ; as grandezas escalares, a densidade de energia ε e a pressão da matéria p , também são funções do tempo.

As equações de Einstein no vácuo no referencial síncrono são

${\ displaystyle R_ {0} ^ {0} = - {\ frac {1} {2}} {\ frac {\ partial \ varkappa _ {\ alpha} ^ {\ alpha}} {\ partial t}} - { \ frac {1} {4}} \ varkappa _ {\ alpha} ^ {\ beta} \ varkappa _ {\ beta} ^ {\ alpha} = 0,}$

( eq. 11 )

${\ displaystyle R _ {\ alpha} ^ {\ beta} = - {\ frac {1} {2 {\ sqrt {-g}}}} {\ frac {\ partial} {\ partial t}} \ left ({ \ sqrt {-g}} \ varkappa _ {\ alpha} ^ {\ beta} \ right) -P _ {\ alpha} ^ {\ beta} = 0,}$

( eq. 12 )

${\ displaystyle R _ {\ alpha} ^ {0} = {\ frac {1} {2}} \ left (\ varkappa _ {\ alpha; \ beta} ^ {\ beta} - \ varkappa _ {\ beta; \ alpha} ^ {\ beta} \ right) = 0,}$

( eq. 13 )

onde é o tensor tridimensional , e P _αβ é o tensor de Ricci tridimensional , que é expresso pelo tensor métrico tridimensional γ _αβ da mesma forma que R _ik é expresso por g _ik ; P _αβ contém apenas as derivadas espaciais (mas não o tempo) de γ _αβ . Usando tríades, para eq. 11 um tem simplesmente ${\ displaystyle \ varkappa _ {\ alpha} ^ {\ beta}}$${\ displaystyle \ varkappa _ {\ alpha} ^ {\ beta} = {\ frac {\ partial \ gamma _ {\ alpha} ^ {\ beta}} {\ partial t}}}$

${\ displaystyle \ varkappa _ {(a) (b)} = {\ frac {\ partial \ eta _ {ab}} {\ partial t}}, \ quad \ varkappa _ {(a)} ^ {(b) } = {\ frac {\ parcial \ eta _ {ac}} {\ parcial t}} \ eta ^ {cb}.}$

Os componentes de P _{( a ) ( b )} podem ser expressos em termos das quantidades η _ab e das constantes de estrutura do grupo usando a representação tétrada do tensor de Ricci em termos de quantidades${\ displaystyle \ lambda _ {abc} = \ left (e _ {(a) i, k} -e _ {(a) k, i} \ right) e _ {(b)} ^ {i} e _ {(c) } ^ {k}}$

${\ displaystyle R _ {(a) (b)} = - {\ frac {1} {2}} \ left (\ lambda _ {ab, c} ^ {c} + \ lambda _ {ba, c} ^ { c} + \ lambda _ {ca, b} ^ {c} + \ lambda _ {cb, a} ^ {c} + \ lambda _ {b} ^ {cd} \ lambda _ {cda} + \ lambda _ { b} ^ {cd} \ lambda _ {dca} - {\ frac {1} {2}} \ lambda _ {b} ^ {cd} \ lambda _ {acd} + \ lambda _ {cd} ^ {c} \ lambda _ {ab} ^ {d} + \ lambda _ {cd} ^ {c} \ lambda _ {ba} ^ {d} \ right).}$

Depois de substituir os símbolos de três índices por símbolos de dois índices C ^ab e as transformações: ${\ displaystyle \ lambda _ {bc} ^ {a} = C_ {bc} ^ {a}}$

${\ displaystyle \ eta _ {ad} \ eta _ {bc} \ eta _ {cf} e ^ {def} = \ eta e_ {abc}, \ quad e_ {abf} e ^ {cdf} = \ delta _ { a} ^ {c} \ delta _ {b} ^ {d} - \ delta _ {a} ^ {d} \ delta _ {b} ^ {c}}$

obtém-se o tensor de Ricci "homogêneo" expresso em constantes de estrutura:

${\ displaystyle P _ {(a)} ^ {(b)} = {\ frac {1} {2 \ eta}} \ left \ {2C ^ {bd} C_ {ad} + C ^ {db} C_ {ad } + C ^ {bd} C_ {da} -C_ {d} ^ {d} \ left (C_ {a} ^ {b} + C_ {a} ^ {b} \ right) + \ delta _ {a} ^ {b} \ left [\ left (C_ {d} ^ {d} \ right) ^ {2} -2C ^ {df} C_ {df} \ right] \ right \}.}$

Aqui, todos os índices são aumentados e diminuídos com o tensor métrico local η _ab

${\ displaystyle C_ {a} ^ {b} = \ eta _ {ac} C ^ {cb}, \ quad C_ {ab} = \ eta _ {ac} \ eta _ {bd} C ^ {cd}.}$

As identidades de Bianchi para o tensor tridimensional P _αβ no espaço homogêneo tomam a forma

${\ displaystyle P_ {b} ^ {c} C_ {ca} ^ {b} + P_ {a} ^ {c} C_ {cb} ^ {b} = 0.}$

Levando em consideração as transformações de derivadas covariantes para quatro vetores arbitrários A _i e quatro tensores A _ik

${\ displaystyle A_ {i; k} e _ {(a)} ^ {i} e _ {(b)} ^ {k} = A _ {(a) (b)} - A ^ {(d)} \ gamma _ {dab},}$

${\ displaystyle A_ {ik; l} e _ {(a)} ^ {i} e _ {(b)} ^ {k} e _ {(c)} ^ {l} = A _ {(a) (b) (c )} - A _ {(b)} ^ {(d)} \ gamma _ {dac} + A _ {(a)} ^ {(d)} \ gamma _ {dbc},}$

as expressões finais para os componentes da tríade do quatro tensor de Ricci são:

${\ displaystyle R_ {0} ^ {0} = - {\ frac {1} {2}} {\ frac {\ partial \ varkappa _ {(a)} ^ {(a)}} {\ partial t}} - {\ frac {1} {4}} \ varkappa _ {(a)} ^ {(b)} \ varkappa _ {(b)} ^ {(a)},}$

( eq. 11a )

${\ displaystyle R _ {(a)} ^ {(b)} = - {\ frac {1} {2 {\ sqrt {\ eta}}}} {\ frac {\ partial} {\ partial t}} \ left ({\ sqrt {\ eta}} \ varkappa _ {(a)} ^ {(b)} \ right) -P _ {(a)} ^ {(b)},}$

( eq. 12a )

${\ displaystyle R _ {(a)} ^ {0} = - {\ frac {1} {2}} \ varkappa _ {(b)} ^ {(c)} \ left (C_ {ca} ^ {b} - \ delta _ {a} ^ {b} C_ {dc} ^ {d} \ right).}$

( eq. 13a )

Ao configurar as equações de Einstein, portanto, não há necessidade de usar expressões explícitas para os vetores de base como funções das coordenadas.

Veja também

• Tabela de grupos de Lie
• Lista de grupos de Lie simples
• Singularidade BKL

Notas

Referências

Bibliografia