Jogo de forma extensiva - Extensive-form game

Um jogo de forma extensiva é uma especificação de um jogo na teoria dos jogos , permitindo (como o nome sugere) a representação explícita de uma série de aspectos-chave, como a sequência dos movimentos possíveis dos jogadores, suas escolhas em cada ponto de decisão, o informações (possivelmente imperfeitas ) que cada jogador tem sobre os movimentos do outro jogador quando toma uma decisão e seus pagamentos para todos os resultados possíveis do jogo. Os jogos de forma extensiva também permitem a representação de informações incompletas na forma de eventos fortuitos modelados como " movimentos por natureza ".

Jogos finitos de forma extensiva

Alguns autores, particularmente em livros introdutórios, inicialmente definem o jogo de forma extensiva como sendo apenas uma árvore de jogo com recompensas (sem informações imperfeitas ou incompletas) e adicionam os outros elementos nos capítulos subsequentes como refinamentos. Enquanto o restante deste artigo segue essa abordagem gentil com exemplos motivadores, apresentamos antecipadamente os jogos de forma extensiva finita conforme (em última análise) construídos aqui. Esta definição geral foi introduzida por Harold W. Kuhn em 1953, que estendeu uma definição anterior de von Neumann a partir de 1928. Seguindo a apresentação de Hart (1992) , um jogo de forma extensiva para n jogadores consiste no seguinte:

Um conjunto finito de n jogadores (racionais)
Uma árvore enraizada , chamada de árvore do jogo
Cada nó terminal (folha) da árvore do jogo tem um n- quinto de payoffs , o que significa que há um payoff para cada jogador no final de cada jogada possível
Uma partição dos nós não terminais da árvore do jogo em n + 1 subconjuntos, um para cada jogador (racional) e com um subconjunto especial para um jogador fictício chamado Chance (ou Natureza). O subconjunto de nós de cada jogador é referido como "nós do jogador". (Um jogo de informações completas, portanto, tem um conjunto vazio de nós de Chance.)
Cada nó do jogador Chance tem uma distribuição de probabilidade sobre suas bordas de saída.
Cada conjunto de nós de um jogador racional é ainda particionado em conjuntos de informações , o que torna certas escolhas indistinguíveis para o jogador ao fazer uma jogada, no sentido de que:
- há uma correspondência de um para um entre as bordas de saída de quaisquer dois nós do mesmo conjunto de informações - assim, o conjunto de todas as bordas de saída de um conjunto de informações é particionado em classes de equivalência , cada classe representando uma escolha possível para o movimento de um jogador em algum ponto—, e
- cada caminho (direcionado) na árvore da raiz a um nó terminal pode cruzar cada conjunto de informações no máximo uma vez
a descrição completa do jogo especificado pelos parâmetros acima é de conhecimento comum entre os jogadores

Uma peça é, portanto, um caminho através da árvore da raiz até um nó terminal. Em qualquer nó não terminal pertencente a Chance, uma ramificação de saída é escolhida de acordo com a distribuição de probabilidade. Em qualquer nó do jogador racional, o jogador deve escolher uma das classes de equivalência para as bordas, o que determina precisamente uma borda de saída, exceto (em geral) o jogador não sabe qual está sendo seguida. (Um observador externo conhecendo as escolhas de todos os outros jogadores até aquele ponto, e a realização dos movimentos da Natureza, pode determinar a borda com precisão.) Uma estratégia pura para um jogador consiste, portanto, em uma seleção - escolher precisamente uma classe de bordas de saída para cada informação conjunto (dele). Em um jogo de informações perfeitas, os conjuntos de informações são singletons . É menos evidente como os payoffs devem ser interpretados em jogos com nós de Chance. Presume-se que cada jogador tenha uma função de utilidade von Neumann – Morgenstern definida para cada resultado do jogo; essa suposição implica que todo jogador racional avaliará um resultado aleatório a priori por sua utilidade esperada .

A apresentação acima, embora defina precisamente a estrutura matemática sobre a qual o jogo é jogado, elimina, no entanto, a discussão mais técnica de formalizar declarações sobre como o jogo é jogado, como "um jogador não pode distinguir entre nós no mesmo conjunto de informações ao tomar uma decisão" . Isso pode ser feito com precisão usando a lógica modal epistêmica ; veja Shoham & Leyton-Brown (2009 , cap. 13) para detalhes.

Um jogo de informação perfeita para dois jogadores em uma árvore de jogo (conforme definido na teoria dos jogos combinatória e inteligência artificial ) pode ser representado como um jogo de forma extensa com resultados (ou seja, ganhar, perder ou empatar ). Exemplos de tais jogos incluem jogo da velha , xadrez e xadrez infinito . Um jogo sobre uma árvore expectminimax , como o gamão , não tem informações imperfeitas (todos os conjuntos de informações são singletons), mas tem jogadas aleatórias. Por exemplo, o pôquer tem movimentos de azar (as cartas sendo distribuídas) e informações imperfeitas (as cartas secretamente mantidas por outros jogadores). ( Binmore 2007 , cap. 2)

Informação perfeita e completa

Uma representação completa de forma extensiva especifica:

os jogadores de um jogo
para cada jogador, todas as oportunidades que eles têm para se mover
o que cada jogador pode fazer em cada um de seus movimentos
o que cada jogador sabe para cada movimento
os pagamentos recebidos por cada jogador para cada combinação possível de movimentos

Um jogo representado de forma extensa

O jogo da direita tem dois jogadores: 1 e 2. Os números em cada nó não terminal indicam a qual jogador esse nó de decisão pertence. Os números por cada nó terminal representam os payoffs para os jogadores (por exemplo, 2,1 representa um payoff de 2 para o jogador 1 e um payoff de 1 para o jogador 2). Os rótulos de cada borda do gráfico são o nome da ação que a borda representa.

O nó inicial pertence ao jogador 1, indicando que o jogador 1 se move primeiro. Jogar de acordo com a árvore é o seguinte: o jogador 1 escolhe entre U e D ; o jogador 2 observa a escolha do jogador 1 e então escolhe entre U ' e D' . Os ganhos são conforme especificado na árvore. Existem quatro resultados representados pelos quatro nós terminais da árvore: (U, U '), (U, D'), (D, U ') e (D, D'). Os payoffs associados a cada resultado, respectivamente, são os seguintes (0,0), (2,1), (1,2) e (3,1).

Se o jogador 1 jogar D , o jogador 2 jogará U ' para maximizar seu pagamento e, portanto, o jogador 1 receberá apenas 1. No entanto, se o jogador 1 jogar U , o jogador 2 maximiza seu pagamento jogando D' e o jogador 1 recebe 2. Jogador 1 prefere 2 a 1 e assim jogará U e o jogador 2 jogará D ' . Este é o equilíbrio perfeito do subjogo .

Informação imperfeita

Uma vantagem de representar o jogo dessa forma é que fica claro qual é a ordem do jogo. A árvore mostra claramente que o jogador 1 se move primeiro e o jogador 2 observa esse movimento. No entanto, em alguns jogos, o jogo não ocorre desta forma. Um jogador nem sempre observa a escolha do outro (por exemplo, os movimentos podem ser simultâneos ou um movimento pode ser oculto). Um conjunto de informações é um conjunto de nós de decisão tais que:

Cada nó do conjunto pertence a um jogador.
Quando o jogo atinge o conjunto de informações, o jogador que está prestes a se mover não consegue diferenciar entre os nós dentro do conjunto de informações; ou seja, se o conjunto de informações contém mais de um nó, o jogador a quem esse conjunto pertence não sabe qual nó do conjunto foi atingido.

Em forma extensa, um conjunto de informações é indicado por uma linha pontilhada conectando todos os nós naquele conjunto ou, às vezes, por um laço desenhado ao redor de todos os nós naquele conjunto.

Um jogo com informações imperfeitas representadas de forma extensa

Se um jogo tiver um conjunto de informações com mais de um membro, esse jogo é considerado como tendo informações imperfeitas . Um jogo com informações perfeitas é tal que, em qualquer estágio do jogo, cada jogador sabe exatamente o que aconteceu no início do jogo; ou seja, todo conjunto de informações é um conjunto único . Qualquer jogo sem informações perfeitas possui informações imperfeitas.

O jogo à direita é o mesmo que o jogo acima, exceto que o jogador 2 não sabe o que o jogador 1 faz quando vem para jogar. O primeiro jogo descrito contém informações perfeitas; o jogo da direita não. Se ambos os jogadores são racionais e ambos sabem que ambos os jogadores são racionais e tudo o que é conhecido por qualquer jogador é conhecido por todos os jogadores (ou seja, o jogador 1 sabe que o jogador 2 sabe que o jogador 1 é racional e o jogador 2 sabe disso, etc. ad infinitum ), o jogo no primeiro jogo será o seguinte: o jogador 1 sabe que se jogar U , o jogador 2 jogará D ' (porque para o jogador 2 um payoff de 1 é preferível a um payoff de 0) e, portanto, o jogador 1 receberá 2. No entanto, se o jogador 1 jogar D , o jogador 2 jogará U ' (porque para o jogador 2 um payoff de 2 é melhor do que um payoff de 1) e o jogador 1 receberá 1. Portanto, no primeiro jogo, o o equilíbrio será ( U , D ' ) porque o jogador 1 prefere receber 2 para 1 e, portanto, jogará U e, portanto, o jogador 2 jogará D' .

No segundo jogo é menos claro: o jogador 2 não pode observar o movimento do jogador 1. O jogador 1 gostaria de enganar o jogador 2 fazendo-o pensar que jogou U quando na verdade jogou D para que o jogador 2 jogue D ' e o jogador 1 receba 3. Na verdade, no segundo jogo há um equilíbrio bayesiano perfeito onde o jogador 1 peças D e o jogador 2 joga U' e leitor de 2 mantém a crença de que o jogador 1 vai certamente jogar D . Nesse equilíbrio, toda estratégia é racional, dadas as crenças defendidas e toda crença é consistente com as estratégias jogadas. Observe como a imperfeição de informações altera o resultado do jogo.

Para resolver mais facilmente esse jogo para o equilíbrio de Nash , ele pode ser convertido para a forma normal . Dado que este é um jogo simultâneo / sequencial , o jogador um e o jogador dois têm, cada um, duas estratégias .

Estratégias do jogador 1: {U, D}
Estratégias do jogador 2: {U ', D'}


Jogador 2 Jogador 1	Para cima '(U')	Baixo '(D')
Para cima (U)	(0,0)	(2, 1 )
Baixo (D)	( 1 , 2 )	( 3 , 1)

Teremos uma matriz dois por dois com uma recompensa única para cada combinação de movimentos. Usando a forma normal de jogo, agora é possível resolver o jogo e identificar estratégias dominantes para ambos os jogadores.

Se o jogador 1 joga para cima (U), o jogador 2 prefere jogar para baixo (D ') (payoff 1> 0)
Se o jogador 1 joga Down (D), o jogador 2 prefere jogar Up (U ') (Payoff 2> 1)
Se o jogador 2 joga para cima (U '), o jogador 1 prefere jogar para baixo (D) (payoff 1> 0)
Se o jogador 2 joga Down (D '), o jogador 1 prefere jogar Down (D) (3> 2)

Essas preferências podem ser marcadas dentro da matriz e qualquer caixa onde ambos os jogadores tenham uma preferência fornece um equilíbrio nash. Este jogo em particular tem uma única solução de (D, U ') com um payoff de (1,2).

Em jogos com espaços de ação infinitos e informações imperfeitas, os conjuntos de informações não singleton são representados, se necessário, inserindo uma linha pontilhada conectando os pontos finais (não nodais) atrás do arco descrito acima ou percorrendo o próprio arco. Na competição de Stackelberg descrita acima, se o segundo jogador não tivesse observado o movimento do primeiro, o jogo não se encaixaria mais no modelo de Stackelberg; seria uma competição de Cournot .

Informação incompleta

Pode ser que um jogador não saiba exatamente quais são os payoffs do jogo ou de que tipo são seus oponentes. Este tipo de jogo possui informações incompletas . De forma extensa, é representado como um jogo com informações completas, mas imperfeitas, usando a chamada transformação Harsanyi . Essa transformação introduz no jogo a noção de escolha da natureza ou escolha de Deus . Considere um jogo que consiste em um empregador considerar se deve contratar um candidato a emprego. A capacidade do candidato ao emprego pode ser uma de duas coisas: alta ou baixa. Seu nível de habilidade é aleatório; eles têm baixa habilidade com probabilidade 1/3 ou alta habilidade com probabilidade 2/3. Nesse caso, é conveniente modelar a natureza como outra espécie de jogador que escolhe a habilidade do requerente de acordo com essas probabilidades. A natureza, entretanto, não tem recompensas. A escolha da natureza é representada na árvore do jogo por um nó não preenchido. As bordas provenientes de um nó de escolha da natureza são rotuladas com a probabilidade do evento que representa ocorrer.

Um jogo com informações incompletas e imperfeitas representadas de forma extensa

O jogo à esquerda contém informações completas (todos os jogadores e recompensas são conhecidos por todos), mas informações imperfeitas (o empregador não sabe qual foi o movimento da natureza). O nó inicial está no centro e não está preenchido , então a natureza se move primeiro. A natureza seleciona com a mesma probabilidade o tipo de jogador 1 (o que neste jogo equivale a selecionar os payoffs no subjogo jogado), t1 ou t2. O jogador 1 possui conjuntos de informações distintos para eles; ou seja, o jogador 1 sabe de que tipo eles são (não precisa ser o caso). No entanto, o jogador 2 não observa a escolha da natureza. Eles não sabem o tipo de jogador 1; entretanto, neste jogo eles observam as ações do jogador 1; ou seja, há informações perfeitas. Na verdade, agora é apropriado alterar a definição acima de informação completa: em cada estágio do jogo, cada jogador sabe o que foi jogado pelos outros jogadores . No caso das informações privadas, cada jogador sabe o que foi jogado pela natureza. Os conjuntos de informações são representados como antes por linhas tracejadas.

Neste jogo, se a natureza selecionar t1 como o tipo do jogador 1, o jogo jogado será como o primeiro jogo descrito, exceto que o jogador 2 não sabe disso (e o próprio fato de que isso atravessa seus conjuntos de informações o desqualifica do status de subjogo ) Existe um que separa o equilíbrio bayesiano perfeito ; ou seja, um equilíbrio em que diferentes tipos fazem coisas diferentes.

Se ambos os tipos jogarem a mesma ação (agrupamento), um equilíbrio não pode ser sustentado. Se ambos jogarem D , o jogador 2 só pode acreditar que estão em qualquer um dos nós do conjunto de informações com probabilidade 1/2 (porque essa é a chance de ver qualquer um dos tipos). O jogador 2 maximiza sua recompensa jogando D ' . No entanto, se eles jogam D' , tipo 2 preferir jogar U . Isso não pode ser um equilíbrio. Se ambos os tipos jogam U , o jogador 2 novamente acredita que eles estão em qualquer um dos nós com probabilidade 1/2. Neste caso o jogador 2 joga D' , mas, em seguida, digite 1 prefere jogar D .

Se tipo 1 desempenha U e digite 2 desempenha D , o jogador 2 vai jogar D' qualquer ação que eles observam, mas, em seguida, digite 1 prefere D . O único equilíbrio é, portanto, com um tipo de jogo D , tipo de jogo 2 L e jogador joga 2 L' se observar D e randomizar se observar L . Por meio de suas ações, o jogador 1 sinalizou seu tipo para o jogador 2.

Definição formal

Formalmente, um jogo finito em forma extensa é uma estrutura onde: ${\ displaystyle \ Gamma = \ langle {\ mathcal {K}}, \ mathbf {H}, [(\ mathbf {H} _ {i}) _ {i \ in {\ mathcal {I}}}], \ {A (H) \} _ {H \ in \ mathbf {H}}, a, \ rho, u \ rangle}$

${\ displaystyle {\ mathcal {K}} = \ langle V, v ^ {0}, T, p \ rangle}$ é uma árvore finita com um conjunto de nós , um nó inicial único , um conjunto de nós terminais ( seja um conjunto de nós de decisão) e uma função predecessora imediata na qual as regras do jogo são representadas, ${\ displaystyle V}$ ${\ displaystyle v ^ {0} \ in V}$ ${\ displaystyle T \ subset V}$ ${\ displaystyle D = V \ setminus T}$ ${\ displaystyle p: V \ rightarrow D}$
${\ displaystyle \ mathbf {H}}$ é uma partição chamada partição de informação, ${\ displaystyle D}$
${\ displaystyle A (H)}$ é um conjunto de ações disponíveis para cada conjunto de informações que forma uma partição no conjunto de todas as ações . ${\ displaystyle H \ in \ mathbf {H}}$ ${\ displaystyle {\ mathcal {A}}}$
${\ displaystyle a: V \ setminus \ {v ^ {0} \} \ rightarrow {\ mathcal {A}}}$ é uma partição de ação que associa cada nó a uma única ação , atendendo a: ${\ displaystyle v}$ ${\ displaystyle a (v)}$

${\ displaystyle \ forall H \ in \ mathbf {H}, \ forall v \ in H}$ , a restrição de on é uma bijeção, com o conjunto de nós sucessores de . ${\ displaystyle a_ {v}: s (v) \ rightarrow A (H)}$ ${\ displaystyle a}$ ${\ displaystyle s (v)}$ ${\ displaystyle s (v)}$ ${\ displaystyle v}$

${\ displaystyle {\ mathcal {I}} = \ {1, ..., I \}}$ é um conjunto finito de jogadores, é (um jogador especial chamado) natureza e é uma partição do jogador do conjunto de informações . Deixe ser um único jogador que faz um movimento no nó . ${\ displaystyle 0}$ ${\ displaystyle (\ mathbf {H} _ {i}) _ {i \ in {\ mathcal {I}} \ cup \ {0 \}}}$ ${\ displaystyle \ mathbf {H}}$ ${\ displaystyle \ iota (v) = \ iota (H)}$ ${\ displaystyle v \ in H}$
${\ displaystyle \ rho = \ {\ rho _ {H}: A (H) \ rightarrow [0,1] | H \ in \ mathbf {H} _ {0} \}}$ é uma família de probabilidades das ações da natureza, e
${\ displaystyle u = (u_ {i}) _ {i \ in {\ mathcal {I}}}: T \ rightarrow \ mathbb {R} ^ {\ mathcal {I}}}$ é uma função de perfil de recompensa.

Espaço infinito de ação

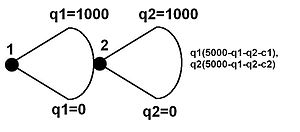
Pode ser que um jogador tenha um número infinito de ações possíveis para escolher em um determinado nó de decisão. O dispositivo usado para representar isso é um arco que une duas arestas que se projetam do nó de decisão em questão. Se o espaço de ação for um continuum entre dois números, os números delimitadores inferior e superior são colocados na parte inferior e superior do arco, respectivamente, geralmente com uma variável que é usada para expressar os ganhos. O número infinito de nós de decisão que podem resultar é representado por um único nó colocado no centro do arco. Um dispositivo semelhante é usado para representar espaços de ação que, embora não sejam infinitos, são grandes o suficiente para se mostrarem impraticáveis para representar com uma borda para cada ação.

Um jogo com infinitos espaços de ação representados de forma extensa

A árvore à esquerda representa tal jogo, seja com espaços de ação infinitos (qualquer número real entre 0 e 5000) ou com espaços de ação muito grandes (talvez qualquer número inteiro entre 0 e 5000). Isso seria especificado em outro lugar. Aqui, será suposto que seja o primeiro e, para concretizar, será suposto que represente duas firmas engajadas na competição de Stackelberg . Os payoffs para as empresas são representados à esquerda, com e conforme a estratégia que adotam e e como algumas constantes (aqui, custos marginais para cada empresa). O equilíbrio perfeito de Nash do subjogo deste jogo pode ser encontrado tomando a primeira derivada parcial de cada função de payoff em relação à variável de estratégia do seguidor (empresa 2) ( ) e encontrando sua melhor função de resposta ,. O mesmo processo pode ser feito para o líder, exceto que, ao calcular seu lucro, ele sabe que a empresa 2 vai jogar a resposta acima e, portanto, isso pode ser substituído em seu problema de maximização. Ele pode então resolver tomando a primeira derivada, rendendo . Alimentando isso na melhor função de resposta da empresa 2, e é o equilíbrio de Nash perfeito do subjogo. ${\ displaystyle q_ {1}}$ ${\ displaystyle q_ {2}}$ ${\ displaystyle c_ {1}}$ ${\ displaystyle c_ {2}}$ ${\ displaystyle q_ {2}}$ ${\ displaystyle q_ {2} (q_ {1}) = {\ tfrac {5000-q_ {1} -c_ {2}} {2}}}$ ${\ displaystyle q_ {1}}$ ${\ displaystyle q_ {1} ^ {*} = {\ tfrac {5000 + c_ {2} -2c_ {1}} {2}}}$ ${\ displaystyle q_ {2} ^ {*} = {\ tfrac {5000 + 2c_ {1} -3c_ {2}} {4}}}$ ${\ displaystyle (q_ {1} ^ {*}, q_ {2} ^ {*})}$

Veja também

Referências

Hart, Sergiu (1992). “Jogos de forma extensiva e estratégica”. Em Aumann, Robert ; Hart, Sergiu (eds.). Manual de teoria dos jogos com aplicações econômicas . 1 . Elsevier. ISBN 978-0-444-88098-7.
Binmore, Kenneth (2007). Jogando para valer: um texto sobre a teoria dos jogos . Oxford University Press US. ISBN 978-0-19-530057-4.
Dresher M. (1961). A matemática dos jogos de estratégia: teoria e aplicações (Capítulo 4: Jogos em forma extensiva, pp74-78). Rand Corp. ISBN 0-486-64216-X
Fudenberg D e Tirole J. (1991) Game theory (Ch3 Extensive form games, pp67-106). MIT press. ISBN 0-262-06141-4
Leyton-Brown, Kevin; Shoham, Yoav (2008), Essentials of Game Theory: A Concise, Multidisciplinary Introduction , San Rafael, CA: Morgan & Claypool Publishers, ISBN 978-1-59829-593-1. Uma introdução matemática de 88 páginas; consulte os Capítulos 4 e 5. Online grátis em muitas universidades.
Luce RD e Raiffa H. (1957). Jogos e decisões: introdução e levantamento crítico. (Ch3: Extensive and Normal Forms, pp39-55). Wiley New York. ISBN 0-486-65943-7
Osborne MJ e Rubinstein A. 1994. Um curso de teoria dos jogos (Ch6 Jogo extensivo com informações perfeitas, pp. 89-115). MIT press. ISBN 0-262-65040-1
Shoham, Yoav; Leyton-Brown, Kevin (2009), Multiagent Systems: Algorithmic, Game-Theoretic, and Logical Foundations , Nova York: Cambridge University Press , ISBN 978-0-521-89943-7. Uma referência abrangente de uma perspectiva computacional; consulte o Capítulo 5. Para download gratuito online .

Leitura adicional

Horst Herrlich (2006). Axioma da escolha . Springer. ISBN 978-3-540-30989-5., 6.1, "Desastres na Teoria dos Jogos" e 7.2 "Mensurabilidade (O Axioma da Determinação)", discute problemas em estender a definição de caso finito para um número infinito de opções (ou movimentos)

Papéis históricos

Neumann, J. (1928). "Zur Theorie der Gesellschaftsspiele". Mathematische Annalen . 100 : 295–320. doi : 10.1007 / BF01448847 .
Harold William Kuhn (2003). Aulas teóricas dos jogos . Princeton University Press. ISBN 978-0-691-02772-2. contém as palestras de Kuhn em Princeton de 1952 (oficialmente não publicado anteriormente, mas em circulação como fotocópias)

Languages

In other projects