Grupo Triângulo - Triangle group

Em matemática , um grupo de triângulos é um grupo que pode ser realizado geometricamente por sequências de reflexos nos lados de um triângulo . O triângulo pode ser um triângulo euclidiano comum , um triângulo na esfera ou um triângulo hiperbólico . Cada grupo de triângulos é o grupo de simetria de uma telha do plano euclidiano , a esfera , ou plano hiperbólico por triângulos congruentes chamados triângulos de Möbius , cada um um domínio fundamental para a ação.

Definição

Deixe- l , m , n ser números inteiros maiores do que ou igual a 2. Um grupo triângulo Δ ( l , m , n ) é um grupo de movimentos do plano euclidiano, a esfera bidimensional, o plano projectiva real, ou a hiperbólica plano gerado pelas reflexões nos lados de um triângulo com ângulos π / l , π / m e ti / n (medido em radianos ). O produto das reflexões em dois lados adjacentes é uma rotação pelo ângulo que é duas vezes o ângulo entre os lados, 2π / l , 2π / m e 2π / n . Portanto, se as reflexões geradoras são rotuladas a , b , c e os ângulos entre elas na ordem cíclica são como dados acima, então as seguintes relações se mantêm:

1. ${\ displaystyle a ^ {2} = b ^ {2} = c ^ {2} = 1}$
2. ${\ displaystyle (ab) ^ {l} = (bc) ^ {n} = (ca) ^ {m} = 1.}$

É um teorema que todas as outras relações entre a, b, c são consequências dessas relações e que Δ ( l, m, n ) é um grupo discreto de movimentos do espaço correspondente. Assim, um grupo triangular é um grupo de reflexão que admite uma apresentação de grupo

${\ displaystyle \ Delta (l, m, n) = \ langle a, b, c \ mid a ^ {2} = b ^ {2} = c ^ {2} = (ab) ^ {l} = (bc ) ^ {n} = (ca) ^ {m} = 1 \ rangle.}$

Um grupo abstrato com esta apresentação é um grupo Coxeter com três geradores.

Classificação

Dados quaisquer números naturais l ,  m ,  n  > 1 exatamente uma das geometrias bidimensionais clássicas (euclidiana, esférica ou hiperbólica) admite um triângulo com os ângulos (π / l, π / m, π / n) e o o espaço é coberto por reflexos do triângulo. A soma dos ângulos do triângulo determina o tipo de geometria pelo teorema de Gauss-Bonnet : é euclidiana se a soma dos ângulos for exatamente π, esférica se exceder π e hiperbólica se for estritamente menor que π. Além disso, quaisquer dois triângulos com os ângulos dados são congruentes. Cada grupo de triângulos determina um ladrilho, que é convencionalmente colorido em duas cores, de modo que quaisquer dois ladrilhos adjacentes tenham cores opostas.

Em termos dos números l ,  m ,  n  > 1, existem as seguintes possibilidades.

O caso euclidiano

${\ displaystyle {\ frac {1} {l}} + {\ frac {1} {m}} + {\ frac {1} {n}} = 1.}$

O grupo de triângulos é o grupo de simetria infinita de um certo mosaico (ou ladrilhos) do plano euclidiano por triângulos cujos ângulos somam π (ou 180 °). Até as permutações, o triplo ( l ,  m ,  n ) é um dos triplos (2,3,6), (2,4,4), (3,3,3). Os grupos de triângulos correspondentes são instâncias de grupos de papéis de parede .

(2,3,6)	(2,4,4)	(3,3,3)
ladrilho hexagonal dividido ao meio	ladrilho quadrado tetrakis	telha triangular
Diagramas mais detalhados, rotulando os vértices e mostrando como a reflexão opera:

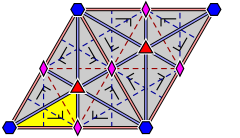
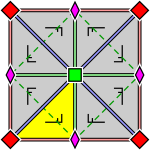
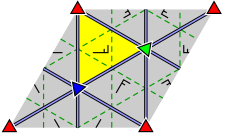
O caso esférico

${\ displaystyle {\ frac {1} {l}} + {\ frac {1} {m}} + {\ frac {1} {n}}> 1.}$

O grupo de triângulos é o grupo de simetria finita de um ladrilho de uma esfera unitária por triângulos esféricos, ou triângulos de Möbius , cujos ângulos somam um número maior que π. Até permutações, o triplo ( l , m , n ) tem a forma (2,3,3), (2,3,4), (2,3,5) ou (2,2, n ), n  > 1. Os grupos de triângulos esféricos podem ser identificados com os grupos de simetria de poliedros regulares no espaço euclidiano tridimensional: Δ (2,3,3) corresponde ao tetraedro , Δ (2,3,4) ao cubo e o octaedro (que tem o mesmo grupo de simetria), Δ (2,3,5) para o dodecaedro e o icosaedro . Os grupos Δ (2,2, n ), n  > 1 de simetria diédrica podem ser interpretados como os grupos de simetria da família dos diedros , que são sólidos degenerados formados por dois n -gonos regulares idênticos unidos, ou hosohedra duplamente , que são formados pela união de n digons em dois vértices.

O revestimento esférico correspondente a um poliedro regular é obtido pela formação da subdivisão baricêntrica do poliedro e pela projeção dos pontos e linhas resultantes na esfera circunscrita. No caso do tetraedro, existem quatro faces e cada face é um triângulo equilátero que é subdividido em 6 pedaços menores pelas medianas que se cruzam no centro. A tesselação resultante tem 4 × 6 = 24 triângulos esféricos (é o cubo esférico disdyakis ).

Esses grupos são finitos, o que corresponde à compactação da esfera - as áreas dos discos na esfera inicialmente crescem em termos de raio, mas acabam cobrindo toda a esfera.

As telhas triangulares são descritas abaixo:

(2,2,2)	(2,2,3)	(2,2,4)	(2,2,5)	(2,2,6)	(2,2, n)
(2,3,3)		(2,3,4)		(2,3,5)

As telhas esféricas correspondentes ao octaedro e ao icosaedro e as telhas esféricas diédricas com n par são centralmente simétricas . Portanto, cada um deles determina um ladrilho do plano projetivo real, um ladrilho elíptico . Seu grupo de simetria é o quociente do grupo de triângulos esféricos pela reflexão através da origem (- I ), que é um elemento central de ordem 2. Como o plano projetivo é um modelo de geometria elíptica , tais grupos são chamados de grupos de triângulos elípticos .

O caso hiperbólico

${\ displaystyle {\ frac {1} {l}} + {\ frac {1} {m}} + {\ frac {1} {n}} <1.}$

O grupo de triângulos é o grupo de simetria infinita de uma telha do plano hiperbólico por triângulos hiperbólicos cujos ângulos somam um número menor que π. Todos os triplos ainda não listados representam tilings do plano hiperbólico. Por exemplo, o triplo (2,3,7) produz o grupo de triângulos (2,3,7) . Existem infinitamente muitos desses grupos; as coisas associadas a alguns valores pequenos:

Plano hiperbólico

Modelo de disco de Poincaré de triângulos de domínio fundamental

Triângulos retângulos de exemplo (2 pq)
(2 3 7)	(2 3 8)	(2 3 9)	(2 3 ∞)
(2 4 5)	(2 4 6)	(2 4 7)	(2 4 8)	(2 4 ∞)
(2 5 5)	(2 5 6)	(2 5 7)	(2 6 6)	(2 ∞ ∞)
Triângulos gerais de exemplo (pqr)
(3 3 4)	(3 3 5)	(3 3 6)	(3 3 7)	(3 3 ∞)
(3 4 4)	(3 6 6)	(3 ∞ ∞)	(6 6 6)	(∞ ∞ ∞)

Grupos de triângulos hiperbólicos são exemplos de grupos cristalográficos não euclidianos e foram generalizados na teoria dos grupos hiperbólicos de Gromov .

Grupos Von Dyck

Denote por D ( l , m , n ) o subgrupo do índice 2 em Δ (l, m, n) gerado por palavras de comprimento par nos geradores. Esses subgrupos são às vezes chamados de grupos de triângulos "comuns" ou grupos de von Dyck , em homenagem a Walther von Dyck . Para triângulos esféricos, euclidianos e hiperbólicos, eles correspondem aos elementos do grupo que preservam a orientação do triângulo - o grupo de rotações. Para triângulos projetivos (elípticos), eles não podem ser interpretados dessa forma, uma vez que o plano projetivo é não orientável, portanto, não há noção de "preservação da orientação". Os reflexos são, no entanto, localmente de orientação reversa (e cada variedade é localmente orientável, porque localmente euclidiana): eles fixam uma linha e em cada ponto da linha são um reflexo através da linha.

O grupo D ( l , m , n ) é definido pela seguinte apresentação:

${\ displaystyle D (l, m, n) = \ langle x, y \ mid x ^ {l}, y ^ {m}, (xy) ^ {n} \ rangle.}$

Em termos dos geradores acima, são x = ab, y = ca, yx = cb . Geometricamente, os três elementos de x , y , xy correspondem a rotações por 2π / l , 2π / m e 2π / n sobre os três vértices do triângulo.

Observe que D ( l , m , n ) ≅ D ( m , l , n ) ≅ D ( n , m , l ), então D ( l , m , n ) é independente da ordem de l , m , n .

Um grupo de von Dyck hiperbólico é um grupo Fuchsiano , um grupo discreto que consiste em isometrias do plano hiperbólico que preservam a orientação.

Peças sobrepostas

Os grupos de triângulos preservam um mosaico por triângulos, ou seja, um domínio fundamental para a ação (o triângulo definido pelas linhas de reflexão), chamado de triângulo de Möbius , e são dados por um triplo de inteiros, ( l , m , n ), - inteiros correspondem a triângulos (2 l , 2 m , 2 n ) que se unem em um vértice. Existem também inclinações por triângulos sobrepostos, que correspondem aos triângulos de Schwarz com números racionais ( l / a , m / b , n / c ), onde os denominadores são coprimes dos numeradores. Isso corresponde a arestas que se encontram em ângulos de a π / l (resp.), Que corresponde a uma rotação de 2 a π / l (resp.), Que tem ordem le é, portanto, idêntica a um elemento de grupo abstrato, mas distinto quando representado por um reflexo.

Por exemplo, o triângulo de Schwarz (2 3 3) produz uma camada de densidade 1 da esfera, enquanto o triângulo (2 3/2 3) produz uma camada de densidade 3 da esfera, mas com o mesmo grupo abstrato. Essas simetrias de ladrilhos sobrepostos não são consideradas grupos de triângulos.

História

Os grupos de triângulos datam pelo menos da apresentação do grupo icosaédrico como o grupo de triângulos (rotacional) (2,3,5) por William Rowan Hamilton em 1856, em seu artigo sobre cálculo icosiano .

Formulários

Vídeo externo
Ladrilhos modulares empenados - visualização do mapa (2,3, ∞) → (2,3,7) transformando os ladrilhos associados.

Os grupos de triângulos surgem na geometria aritmética . O grupo modular é gerado por dois elementos, S e T , sujeitos às relações S ² = ( ST ) ³ = 1 (nenhuma relação em T ), é o grupo de triângulos rotacionais (2,3, ∞) e mapeia em todos os triângulos grupos (2,3, n ) adicionando a relação T ⁿ = 1. Mais geralmente, o grupo de Hecke H _q é gerado por dois elementos, S e T , sujeitos às relações S ² = ( ST ) ^q = 1 (não relação em T ), é o grupo de triângulo rotacional (2, q , ∞), e mapeia em todos os grupos de triângulo (2, q , n ) adicionando a relação T ⁿ = 1 o grupo modular é o grupo de Hecke H ₃ . Na teoria de dessins d'enfants de Grothendieck , uma função Belyi dá origem a uma tesselação de uma superfície de Riemann por domínios de reflexão de um grupo de triângulos.

Todos os 26 grupos esporádicos são quocientes de grupos triangulares, dos quais 12 são grupos de Hurwitz (quocientes do grupo (2,3,7)).

Veja também

• Triângulo de Schwarz
• O mapa de triângulos de Schwarz é um mapa de triângulos até o meio plano superior .
• Teoria geométrica do grupo

Referências

links externos

• Robert Dawson Algumas tilings esféricas (sem data, anterior a 2004) (Mostra uma série de tilings esféricas interessantes, a maioria das quais não são tilings de grupos triangulares.)
• Elizabeth r chen triângulo grupos (2010) imagens de fundo da área de trabalho

Este artigo incorpora material de grupos Triangle no PlanetMath , que é licenciado sob a licença Creative Commons Atribuição / Compartilhamento pela mesma Licença .