Functores adjuntos - Adjoint functors
Em matemática , especificamente na teoria das categorias , adjunção é uma relação que dois functores podem ter. Dois functores que estão nessa relação são conhecidos como functores adjuntos , sendo um o adjunto esquerdo e o outro o adjunto direito . Pares de functores adjuntos são onipresentes na matemática e muitas vezes surgem de construções de "soluções ótimas" para certos problemas (ou seja, construções de objetos com uma certa propriedade universal ), como a construção de um grupo livre em um conjunto de álgebra, ou a construção da compactação Stone – Čech de um espaço topológico em topologia.
Por definição, uma adjunção entre categorias e é um par de functores (assumidos como covariantes )
- e
e, para todos os objetos em e em uma bijeção entre os respectivos conjuntos de morfismo
de modo que esta família de bijeções é natural em e . Naturalidade aqui significa que há isomorfismos naturais entre o par de functors e de um fixo em , e também do par de functors e por tempo determinado em .
O functor é chamado de functor adjunto à esquerda ou adjunto à esquerda de , enquanto é chamado de functor adjunto à direita ou adjunto à direita de .
Uma adjunção entre categorias e é um tanto semelhante a uma "forma fraca" de uma equivalência entre e , e de fato toda equivalência é uma adjunção. Em muitas situações, uma adjunção pode ser "atualizada" para uma equivalência, por uma modificação natural adequada das categorias e functores envolvidos.
Terminologia e notação
Duas raízes diferentes estão sendo usadas: "adjunto" e "adjunto". Do Oxford Short English dictionary, "adjunto" vem do latim, "adjoint" vem do francês.
Em Mac Lane, Categorias para o matemático ativo , cap. 4, "Adjoints", pode-se verificar o seguinte uso. Dada uma família
de bijeções hom-set, chamamos de "adjunção" ou "adjunção entre e ". Se for uma seta , é o "adjunto" direito de (p. 81). O functor é deixado "adjunto" para , e é direito adjunto para . (Observe que pode ter um adjunto direito que é bastante diferente ; veja abaixo um exemplo.)
Em geral, as frases " é um adjunto à esquerda" e " tem um adjunto à direita" são equivalentes.
Se F for deixado adjacente a G , também escrevemos
A terminologia vem da ideia de espaço de Hilbert de operadores adjuntos , com , que é formalmente semelhante à relação acima entre conjuntos hom. A analogia com mapas adjacentes de espaços de Hilbert pode ser feita com precisão em certos contextos.
Introdução e Motivação
O slogan é "Os functores adjuntos surgem em todos os lugares".
- Saunders Mac Lane, categorias para o matemático trabalhador
A longa lista de exemplos neste artigo indica que construções matemáticas comuns são muitas vezes functores adjuntos. Conseqüentemente, teoremas gerais sobre functores adjuntos esquerda / direita codificam os detalhes de muitos resultados úteis e não triviais. Tais teoremas gerais incluem a equivalência das várias definições de functores adjuntos, a singularidade de um adjunto direito para um dado adjunto esquerdo, o fato de que os functores adjunto esquerdo / direito preservam respectivamente colimites / limites (que também são encontrados em todas as áreas da matemática) , e os teoremas gerais do functor adjunto dando condições sob as quais um dado functor é um adjunto esquerdo / direito.
Soluções para problemas de otimização
Em certo sentido, um functor adjunto é uma maneira de fornecer a solução mais eficiente para algum problema por meio de um método que é formular . Por exemplo, um problema fundamental na teoria dos anéis é como transformar um RNG (que é como um anel que pode não ter uma identidade multiplicativa) em um anel . A maneira mais eficiente é juntar um elemento '1' ao anel, juntar todos (e apenas) os elementos que são necessários para satisfazer os axiomas do anel (por exemplo, r +1 para cada r no anel), e não impor relações em o anel recém-formado que não é forçado por axiomas. Além disso, essa construção é estereotipada no sentido de que funciona essencialmente da mesma maneira para qualquer anel.
Isso é um tanto vago, embora sugestivo, e pode ser tornado preciso na linguagem da teoria das categorias: uma construção é mais eficiente se satisfaz uma propriedade universal , e é formular se define um functor . As propriedades universais vêm em dois tipos: propriedades iniciais e propriedades do terminal. Visto que essas são noções duais , é necessário discutir apenas uma delas.
A idéia de usar uma propriedade inicial é definir o problema em termos de alguma categoria auxiliar E , para que o problema corresponde mão para encontrar um objeto inicial de E . Isso tem a vantagem de que a otimização - a sensação de que o processo encontra a solução mais eficiente - significa algo rigoroso e reconhecível, como a obtenção de um supremo . A categoria E também é estereotipada nesta construção, uma vez que é sempre a categoria de elementos do functor para os quais se está construindo um adjunto.
De volta ao nosso exemplo: pegue o dado Rng R , e faça uma categoria E cujos objetos são rng homomorfismos R → S , com S um anel tendo uma identidade multiplicativa. Os morfismos em E entre R → S 1 e R → S 2 são triângulos comutativos da forma ( R → S 1 , R → S 2 , S 1 → S 2 ) onde S 1 → S 2 é um mapa de anéis (que preserva a identidade). (Observe que esta é precisamente a definição da categoria de vírgula de R sobre a inclusão de anéis unitários em rng.) A existência de um morfismo entre R → S 1 e R → S 2 implica que S 1 é pelo menos uma solução tão eficiente como S 2 para o nosso problema: S 2 pode ter mais elementos adjacentes e / ou mais relações não impostas por axiomas do que S 1 . Portanto, a afirmação de que um objeto R → R * é inicial em E , ou seja, que existe um morfismo dele para qualquer outro elemento de E , significa que o anel R * é a solução mais eficiente para o nosso problema.
Os dois fatos de que esse método de transformar rngs em anéis é mais eficiente e estereotipado podem ser expressos simultaneamente dizendo que ele define um functor adjunto . Mais explicitamente: deixe F denotar o processo acima de anexar uma identidade a um rng, então F ( R ) = R * . Vamos L denotar o processo de “esquecimento" se um anel S tem uma identidade e considerando que simplesmente como um rng, de modo essencialmente L ( S ) = S . Então F é o functor adjunto esquerdo de G .
Observe, entretanto, que ainda não construímos R * ; é um fato algébrico importante e não totalmente trivial que tal functor adjunto à esquerda R → R * realmente exista.
Simetria de problemas de otimização
Também é possível começar com o functor F e fazer a seguinte (vaga) questão: existe um problema para o qual F é a solução mais eficiente?
A noção de que F é a solução mais eficiente para o problema proposto por G é, em certo sentido rigoroso, equivalente à noção de que G apresenta o problema mais difícil que F resolve.
Isto dá a intuição por trás do fato de que funtores adjuntos ocorrem em pares: se F é adjunto esquerdo de G , então G é adjunto direito a F .
Definições formais
Existem várias definições equivalentes para functores adjuntos:
- As definições por meio de morfismos universais são fáceis de declarar e requerem verificações mínimas ao construir um functor adjunto ou provar que dois functores são adjunto. Eles também são os mais análogos à nossa intuição envolvendo otimizações.
- A definição via hom-sets torna a simetria a mais aparente, e é a razão para usar a palavra adjunta .
- A definição via adjunção de unidade de contagem é conveniente para provas sobre functores que são conhecidos por serem adjuntos, porque fornecem fórmulas que podem ser manipuladas diretamente.
A equivalência dessas definições é bastante útil. Os functores adjuntos surgem em todos os lugares, em todas as áreas da matemática. Uma vez que a estrutura em qualquer uma dessas definições dá origem às estruturas nas outras, alternar entre elas faz uso implícito de uma grande quantidade de detalhes tediosos que, de outra forma, teriam de ser repetidos separadamente em cada área de assunto.
Convenções
A teoria dos adjuntos tem os termos esquerda e direita em sua base, e há muitos componentes que vivem em uma das duas categorias C e D que estão sendo consideradas. Portanto, pode ser útil escolher as letras em ordem alfabética de acordo com se elas moram na categoria C de "mão esquerda" ou na categoria D de "mão direita" , e também anotá-las nessa ordem sempre que possível.
Neste artigo, por exemplo, as letras X , F , f , ε denotam consistentemente coisas que vivem na categoria C , as letras Y , G , g , η denotam consistentemente coisas que vivem na categoria D , e sempre que possível tais as coisas serão referidas em ordem da esquerda para a direita (um functor F : D → C pode ser pensado como "vivo" onde estão suas saídas, em C ).
Definição via morfismos universais
Por definição, um functor é um functor adjunto esquerdo se para cada objeto no existe uma morphism universal a partir de . Explicado, isso significa que para cada objeto em existe um objeto em e um morfismo tal que para cada objeto em e cada morfismo existe um morfismo único com .
A última equação é expressa pelo seguinte diagrama comutativo :
Nesta situação, pode-se mostrar que pode ser transformado em um functor de uma forma única tal que para todos os morfismos em ; é então chamado de adjunto esquerdo de .
Da mesma forma, podemos definir functores adjuntos à direita. Um functor é um functor adjunto direito se, para cada objeto em , existe um morfismo universal de a . Explicado, isso significa que para cada objeto em , existe um objeto em e um morfismo tal que para cada objeto em e cada morfismo existe um morfismo único com .
Novamente, isso pode ser exclusivamente transformado em um functor, de modo que para um morfismo em ; é então chamado de adjunto à direita .
É verdade, como a terminologia indica, que é deixado junto a se e somente se é direito adjacente a .
Essas definições por meio de morfismos universais são frequentemente úteis para estabelecer que um dado functor é adjacente à esquerda ou à direita, porque eles são minimalistas em seus requisitos. Eles também são intuitivamente significativos, pois encontrar um morfismo universal é como resolver um problema de otimização.
Definição via adjunção Hom-set
Uma adjunção hom-set entre duas categorias C e D consiste em dois functores F : D → C e G : C → D e um isomorfismo natural
- .
Isso especifica uma família de bijeções
Para todos os objetos X em C e Y em D .
Nesta situação, F é adjunto esquerdo ao G e G é adjunto direito a F .
Esta definição é um compromisso lógico, pois é um pouco mais difícil de satisfazer do que as definições de morfismo universal e tem menos implicações imediatas do que a definição de unidade de contagem. É útil por causa de sua óbvia simetria e como um trampolim entre as outras definições.
Para interpretar Φ como um isomorfismo natural , deve-se reconhecer hom C ( F -, -) e hom D (-, G -) como functores. Na verdade, ambos são bifuncionais de D op × C a Conjunto (a categoria dos conjuntos ). Para obter detalhes, consulte o artigo sobre functores hom . Explicitamente, a naturalidade de Φ significa que para todos os morfismos f : X → X ′ em C e todos os morfismos g : Y ′ → Y em D o seguinte diagrama comuta :
As setas verticais neste diagrama são aquelas induzidas por composição. Formalmente, Hom ( Fg , f ): Hom C ( FY , X ) → Hom C ( FY ′ , X ′ ) é dado por h → f o h o Fg para cada h em Hom C ( FY , X ). Hom ( g , Gf ) é semelhante.
Definição via adjunção de unidade de contagem
Uma adjunção de unidade de contagem entre duas categorias C e D consiste em dois functores F : D → C e G : C → D e duas transformações naturais
respectivamente chamados de contagem e unidade da adjunção (terminologia da álgebra universal ), de modo que as composições
são as transformações de identidade 1 F e 1 G em F e G, respectivamente.
Nesta situação, dizemos que F é deixado adjacente a G e G é direito adjacente a F , e podemos indicar essa relação por escrito ou simplesmente .
Na forma de equação, as condições acima em ( ε , η ) são as equações de unidade de contagem
o que significa que para cada X em C e cada Y em D ,
- .
Observe que denota o functor de identificação na categoria , denota a transformação natural de identidade do functor F para ele mesmo e denota o morfismo de identidade do objeto FY .
Essas equações são úteis para reduzir as provas sobre functores adjuntos a manipulações algébricas. Às vezes, são chamadas de identidades triangulares ou de equações em zigue-zague por causa da aparência dos diagramas de string correspondentes . Uma maneira de lembrá-los é primeiro anotar a equação absurda e, em seguida, preencher F ou G em uma das duas maneiras simples que tornam as composições definidas.
Nota: O uso do prefixo "co" na contagem aqui não é consistente com a terminologia de limites e colimites, porque um colimito satisfaz uma propriedade inicial enquanto os morfismos contados irão satisfazer as propriedades terminais , e duplamente. O termo unidade aqui é emprestado da teoria das mônadas, onde se parece com a inserção da identidade 1 em um monóide.
História
A ideia de functores adjuntos foi introduzida por Daniel Kan em 1958. Como muitos dos conceitos da teoria das categorias, foi sugerida pelas necessidades da álgebra homológica , que na época era dedicada aos cálculos. Aqueles que se deparam com apresentações organizadas e sistemáticas do assunto devem ter notado relações como
- hom ( F ( X ), Y ) = hom ( X , G ( Y ))
na categoria de grupos abelianos , onde F era o functor (ou seja, tome o produto tensorial com A ), e G era o functor hom ( A , -) (agora conhecido como adjunção tensor-hom ). O uso do sinal de igual é um abuso de notação ; esses dois grupos não são realmente idênticos, mas existe uma maneira natural de identificá-los . Pode ser visto para ser natural com base, em primeiro lugar, que estas são duas descrições alternativas dos mapeamentos bilineares de X × A a Y . Isso é, no entanto, algo particular para o caso do produto tensorial. Na teoria das categorias, a 'naturalidade' da bijeção está incluída no conceito de isomorfismo natural .
Ubiquidade
Se começarmos a procurar por esses pares adjuntos de functores, eles acabarão sendo muito comuns na álgebra abstrata e em outros lugares também. A seção de exemplo abaixo fornece evidências disso; além disso, as construções universais , que podem ser mais familiares para alguns, dão origem a vários pares adjacentes de functores.
De acordo com o pensamento de Saunders Mac Lane , qualquer ideia, como functores adjuntos, que ocorre amplamente o suficiente em matemática deve ser estudada por si mesma.
Os conceitos podem ser julgados de acordo com seu uso na resolução de problemas, bem como em seu uso na construção de teorias. A tensão entre essas duas motivações foi especialmente grande durante os anos 1950, quando a teoria das categorias foi inicialmente desenvolvida. Entra Alexander Grothendieck , que usou a teoria das categorias para obter orientações da bússola em outros trabalhos - em análise funcional , álgebra homológica e, finalmente, geometria algébrica .
É provavelmente errado dizer que ele promoveu o conceito de functor adjunto isoladamente: mas o reconhecimento do papel da adjunção era inerente à abordagem de Grothendieck. Por exemplo, uma de suas principais realizações foi a formulação da dualidade de Serre em forma relativa - vagamente, em uma família contínua de variedades algébricas. Toda a prova girou em torno da existência de um adjunto de direito para um determinado functor. Isso é algo inegavelmente abstrato e não construtivo, mas também poderoso à sua maneira.
Exemplos
Grupos livres
A construção de grupos livres é um exemplo comum e esclarecedor.
Seja F : Set → Grp o functor atribuindo a cada conjunto Y o grupo livre gerado pelos elementos de Y , e seja G : Grp → Set o functor esquecido , que atribui a cada grupo X seu conjunto subjacente. Então F é deixado adjacente a G :
Morfismos iniciais. Para cada conjunto de Y , o conjunto GFY é apenas o conjunto subjacente do grupo livre FY gerado por Y . Seja o mapa definido dado por "inclusão de geradores". Este é um morfismo inicial do Y para L , porque qualquer mapa conjunto de Y para o conjunto subjacente GW de alguns grupo W factor de vontade através através de um grupo único homomorphism de FY para W . Esta é precisamente a propriedade universal do grupo livre em Y .
Morfismos terminais. Para cada grupo X , o grupo FGX é o grupo livre gerado livremente por GX , os elementos de X . Seja o homomorfismo de grupo que envia os geradores de FGX aos elementos de X aos quais eles correspondem, que existe pela propriedade universal de grupos livres. Então, cada um é um morfismo terminal de F a X , porque qualquer homomorfismo de grupo de um grupo livre FZ a X será fatorado por meio de um mapa de conjunto único de Z a GX . Isso significa que ( F , G ) é um par adjacente.
Adjunto Hom-set. Os homomorfismos de grupo do grupo livre FY para um grupo X correspondem precisamente aos mapas do conjunto Y para o conjunto GX : cada homomorfismo de FY para X é totalmente determinado por sua ação sobre os geradores, outra reafirmação da propriedade universal dos grupos livres. Pode-se verificar diretamente que essa correspondência é uma transformação natural, o que significa que é uma adjunção hom-set do par ( F , G ).
adjunção de unidade de contagem. Também se pode verificar diretamente que ε e η são naturais. Então, uma verificação direta de que eles formam um adjunto de unidade de contagem é a seguinte:
A primeira equação de unidade de contagem diz que para cada conjunto Y a composição
deve ser a identidade. O grupo intermediário FGFY é o grupo livre gerado livremente pelas palavras do grupo livre FY . (Pense nessas palavras colocadas entre parênteses para indicar que são geradores independentes.) A seta é o homomorfismo de grupo de FY para FGFY enviando cada gerador y de FY para a palavra correspondente de comprimento um ( y ) como um gerador de FGFY . A seta é o homomorfismo de grupo de FGFY para FY enviando cada gerador para a palavra de FY a que corresponde (então este mapa está "retirando parênteses"). A composição desses mapas é de fato a identidade no FY .
A segunda equação conta -unidade diz que para cada grupo X a composição
deve ser a identidade. O conjunto intermediário GFGX é apenas o conjunto básico do FGX . A seta é o mapa do conjunto "inclusão de geradores" do conjunto GX para o conjunto GFGX . A seta é o conjunto de mapas de GFGX para GX que fundamenta o homomorfismo de grupo enviando cada gerador de FGX para o elemento de X a que corresponde ("descartar parênteses"). A composição desses mapas é de fato a identidade no GX .
Construções livres e functores esquecidos
Objetos livres são todos exemplos de um adjunto esquerdo para um functor esquecido que atribui a um objeto algébrico seu conjunto subjacente. Esses functores livres algébricos têm geralmente a mesma descrição que na descrição detalhada da situação do grupo livre acima.
Functores diagonais e limites
Produtos , produtos fibrosos , equalizadores e grãos são todos exemplos da noção categórica de um limite . Qualquer functor de limite é diretamente adjacente a um functor diagonal correspondente (desde que a categoria tenha o tipo de limites em questão), e a contagem da adjunção fornece os mapas de definição do objeto de limite (ou seja, do functor diagonal no limite, no categoria do functor). Abaixo estão alguns exemplos específicos.
- Produtos Seja Π: Grp 2 → Grp o functor que atribui a cada par ( X 1 , X 2 ) o grupo de produtos X 1 × X 2 , e seja Δ: Grp → Grp 2 o functor diagonal que atribui a cada grupo X o par ( X , X ) na categoria de produto Grp 2 . A propriedade universal do grupo de produtos mostra que Π é adjunto à direita de Δ. A contagem deste adjunção é o par de definição de mapas de projeção de X 1 × X 2 a X 1 e X 2 que definem o limite, e a unidade é a inclusão diagonal de um grupo X em X × X (mapeamento de x a (x , x)).
- O produto cartesiano dos conjuntos , o produto dos anéis, o produto dos espaços topológicos etc. seguem o mesmo padrão; ele também pode ser estendido de maneira direta a mais do que apenas dois fatores. Mais geralmente, qualquer tipo de limite é adjacente a um functor diagonal.
- Kernels. Considere a categoria D de homomorfismos de grupos abelianos. Se f 1 : A uma → B 1 e f 2 : Um 2 → B 2 são dois objectos de D , em seguida, um morfismo de f 1 a f 2 é um par ( g Um , g B ) de morphisms tal que g B f 1 = f 2 g A . Seja G : D → Ab o functor que atribui a cada homomorfismo seu núcleo e seja F : Ab → D o functor que mapeia o grupo A para o homomorfismo A → 0. Então G é diretamente adjacente a F , que expressa o universal propriedade dos grãos. A contagem deste adjunção é a incorporação de definição do kernel de um homomorfismo no domínio do homomorfismo, e a unidade é o morfismo que identifica um grupo A com o kernel do homomorfismo A → 0.
- Uma variação adequada deste exemplo também mostra que os functores do kernel para espaços vetoriais e para módulos são adjuntos corretos. Analogamente, pode-se mostrar que os functores cokernel para grupos abelianos, espaços vetoriais e módulos são deixados adjunto.
Colimites e functores diagonais
Co-produtos , coprodutos Fibred , coequalizador e conúcleos são exemplos da noção categórica de um colimit . Qualquer functor colimito é deixado adjunto a um functor diagonal correspondente (desde que a categoria tenha o tipo de colimite em questão), e a unidade da adjunção fornece os mapas de definição para o objeto colimito. Abaixo estão alguns exemplos específicos.
- Coprodutos. Se F : Ab 2 → Ab atribui a cada par ( X 1 , X 2 ) de grupos abelianos sua soma direta , e se G : Ab → Ab 2 é o functor que atribui a cada grupo abeliano Y o par ( Y , Y ) , então F é deixado adjacente a G , novamente uma consequência da propriedade universal das somas diretas. A unidade deste par adjunto é o par de definição de mapas de inclusão de X 1 e X 2 na soma direta, e a contagem é o mapa aditivo da soma direta de ( X , X ) de volta para X (enviando um elemento ( a , b ) da soma direta ao elemento a + b de X ).
- Exemplos análogos são dados pela soma direta de espaços vetoriais e módulos , pelo produto livre de grupos e pela união disjunta de conjuntos.
Outros exemplos
Álgebra
- Juntando uma identidade a um rng . Este exemplo foi discutido na seção de motivação acima. Dado um rng R , um elemento de identidade multiplicativo pode ser adicionado tomando R x Z e definindo um produto Z -bilinear com (r, 0) (0,1) = (0,1) (r, 0) = (r, 0), (r, 0) (s, 0) = (rs, 0), (0,1) (0,1) = (0,1). Isso constrói um adjunto esquerdo para o functor levando um anel para o anel subjacente.
- Unindo uma identidade a um semigrupo . Da mesma forma, dado um semigrupo S , podemos adicionar um elemento de identidade e obter um monóide tomando a união disjunta S {1} e definindo uma operação binária nela de modo que estenda a operação em S e 1 é um elemento de identidade. Essa construção fornece um functor que é um adjunto esquerdo do functor levando um monóide para o semigrupo subjacente.
- Extensões de anel. Suponha que R e S sejam anéis, e ρ: R → S é um homomorfismo de anel . Então S pode ser visto como um módulo R (à esquerda) , e o produto tensorial com S produz um functor F : R - Mod → S - Mod . Então F é deixado adjacente ao functor esquecido G : S - Mod → R - Mod .
- Produtos tensores . Se R é um anel e M é ummódulo R direito, então o produto tensorial com M produz um functor F : R - Mod → Ab . O functor L : Ab → R - Mod , definido por L ( A ) = hom Z ( M , A ) para cada grupo abeliano A , é um adjunto direito para F .
- De monóides e grupos a anéis. O anel monóide integrante construção dá um functor de monoides aos anéis. Este functor é deixado adjacente ao functor que associa a um determinado anel seu monóide multiplicativo subjacente. Da mesma forma, a construção do anel de grupo integral produz um functor de grupos para anéis, à esquerda adjacente ao functor que atribui a um determinado anel seu grupo de unidades . Um pode também começar com um campo K e considerar a categoria de K - álgebras em vez de na categoria de anéis, para obter os anéis monoid e de grupo sobre K .
- Campo de frações. Considere a categoria Dom m de domínios integrais com morfismos injetivos. O functor esquecido Campo → Dom m de campos tem um adjunto à esquerda - ele atribui a cada domínio integral seu campo de frações .
- Anéis polinomiais . Seja Anel * a categoria de anéis comutativos pontiagudos com unidade (pares (A, a) onde A é um anel, a ∈ A e morfismos preservam os elementos distintos). O functor esquecido G: Ring * → Ring tem um adjunto à esquerda - ele atribui a cada anel R o par (R [x], x) onde R [x] é o anel polinomial com coeficientes de R.
- Abelianização . Considere o functor de inclusão G : Ab → Grp da categoria de grupos abelianos para a categoria de grupos . Possui um adjunto à esquerda denominado abelianização que atribui a cada grupo G o grupo quociente G ab = G / [ G , G ].
- O grupo Grothendieck . Na teoria K , o ponto de partida é observar que a categoria de fibrados vetoriais em um espaço topológico tem uma estrutura monóide comutativa sob soma direta . Pode-se fazer um grupo abeliano desse monóide, o grupo Grothendieck , adicionando formalmente um inverso aditivo para cada feixe (ou classe de equivalência). Alternativamente, pode-se observar que o functor que para cada grupo leva o monóide subjacente (ignorando os inversos) tem um adjunto esquerdo. Esta é uma construção definitiva, de acordo com a discussão da terceira seção acima. Ou seja, pode-se imitar a construção de números negativos ; mas existe a outra opção de um teorema da existência . Para o caso de estruturas algébricas finitárias, a própria existência pode ser referida à álgebra universal , ou teoria do modelo ; naturalmente, também há uma prova adaptada à teoria das categorias.
- Reciprocidade de Frobenius na teoria da representação de grupos : ver representação induzida . Este exemplo prefigurou a teoria geral em cerca de meio século.
Topologia
- Um functor com um adjunto esquerdo e direito. Seja G o functor de espaços topológicos para conjuntos que associam a cada espaço topológico seu conjunto subjacente (isto é, esquecendo a topologia). L tem um adjunto esquerdo F , criando o espaço discreto sobre um conjunto Y , e um adjunto direito H criando a topologia trivial em Y .
- Suspensões e espaços em loop. Dados os espaços topológicos X e Y , o espaço [ SX , Y ] das classes de homotopia dos mapas da suspensão SX de X a Y é naturalmente isomórfico ao espaço [ X , Ω Y ] das classes de homotopia dos mapas de X ao espaço do loop Ω Y de Y . O functor de suspensão é, portanto, deixado adjacente ao functor de espaço de loop na categoria de homotopia , um fato importante na teoria da homotopia .
- Compactação Stone – Čech. Seja KHaus a categoria de espaços compactos de Hausdorff e G : KHaus → Top o functor de inclusão para a categoria de espaços topológicos . Então G tem um F adjunto à esquerda : Top → KHaus , a compactação Stone – Čech . A unidade deste par adjacente produz um mapa contínuo de cada espaço topológico X em sua compactação Stone-Čech.
- Imagens diretas e inversas de polias. Cada mapa contínuo f : X → Y entre espaços topológicos induz um functor f ∗ da categoria de feixes (de conjuntos, ou grupos abelianos, ou anéis ...) em X para a categoria correspondente de feixes em Y , o functor de imagem direta . Ele também induz um functor f −1 da categoria de feixes de grupos abelianos em Y para a categoria de feixes de grupos abelianos em X , o functor de imagem inversa . f −1 é deixado adjacente a f ∗ . Aqui, um ponto mais sutil é que o adjunto esquerdo para feixes coerentes será diferente daquele para feixes (de conjuntos).
- Soberificação. O artigo sobre a dualidade de Stone descreve uma adjunção entre a categoria dos espaços topológicos e a categoria dos espaços sóbrios que é conhecida como sobriedade. Notavelmente, o artigo também contém uma descrição detalhada de outro adjunto que prepara o caminho para a famosa dualidade de espaços sóbrios e locais espaciais, explorados em topologia inútil .
Posets
Cada conjunto parcialmente ordenado pode ser visto como uma categoria (onde os elementos da poset se tornam objetos da categoria e temos um único morfismo de x para y se e somente se x ≤ y ). Um par de functores adjuntos entre dois conjuntos parcialmente ordenados é chamado de conexão de Galois (ou, se for contravariante, de conexão de Galois de antítono ). Veja aquele artigo para uma série de exemplos: o caso da teoria de Galois , é claro, é um dos principais. Qualquer conexão de Galois dá origem a operadores de fechamento e a bijeções que preservam a ordem inversa entre os elementos fechados correspondentes.
Como é o caso dos grupos de Galois, o real interesse freqüentemente reside em refinar uma correspondência para uma dualidade (isto é , isomorfismo de ordem de antítono ). Um tratamento da teoria de Galois ao longo dessas linhas por Kaplansky foi influente no reconhecimento da estrutura geral aqui.
O caso de pedido parcial reduz as definições de adjunção de maneira bastante perceptível, mas pode fornecer vários temas:
- adjunções podem não ser dualidades ou isomorfismos, mas são candidatos para upgrade para esse status
- operadores de fechamento podem indicar a presença de adjunções, como mônadas correspondentes (cf. os axiomas de fechamento de Kuratowski )
- um comentário muito geral de William Lawvere é que a sintaxe e a semântica são adjacentes: considere C como o conjunto de todas as teorias lógicas (axiomatizações) e D como o conjunto de poder do conjunto de todas as estruturas matemáticas. Para uma teoria T em C , seja G ( T ) o conjunto de todas as estruturas que satisfazem os axiomas T ; para um conjunto de estruturas matemáticas S , deixar F ( S ) ser a axiomatization mínima de S . Podemos então dizer que S é um subconjunto de G ( T ) se e somente se F ( S ) implica logicamente T : a "semântica functor" G é adjunto direito ao "functor sintaxe" F .
- divisão é (em geral) a tentativa de inverter a multiplicação, mas em situações em que isso não é possível, muitas vezes tentamos construir um adjunto : o quociente ideal é adjacente à multiplicação por ideais de anel e a implicação na lógica proposicional é adjacente à conjunção lógica .
Teoria da categoria
- Equivalências. Se F : D → C é uma equivalência de categorias , então temos uma equivalência inversa G : C → D , e os dois functores F e G formam um par adjunto. A unidade e a contagem são isomorfismos naturais neste caso.
- Uma série de complementos. O functor π 0 que atribui a uma categoria seu conjunto de componentes conectados é adjacente à esquerda do functor D, que atribui a um conjunto a categoria discreta naquele conjunto. Além disso, D é adjunto à esquerda do functor de objeto U, que atribui a cada categoria seu conjunto de objetos, e finalmente U é adjunto à esquerda de A, que atribui a cada conjunto a categoria indiscreta desse conjunto.
- Objeto exponencial . Em um cartesiano categoria fechada a endofunctor C → C dada por - × Um tem um adjunto direito - A . Este par é freqüentemente referido como currying e sem pressa; em muitos casos especiais, eles também são contínuos e formam um homeomorfismo.
Lógica categórica
- Quantificação. Se for um predicado unário expressando alguma propriedade, então uma teoria de conjuntos suficientemente forte pode provar a existência do conjunto de termos que cumprem a propriedade. Um subconjunto adequado e a injeção associada de em são caracterizados por um predicado que expressa uma propriedade estritamente mais restritiva.
- O papel dos quantificadores na lógica de predicados é formar proposições e também expressar predicados sofisticados por meio de fórmulas de fechamento com possivelmente mais variáveis. Por exemplo, considere um predicado com duas variáveis abertas do tipo e . Usando um quantificador para fechar , podemos formar o conjunto
- de todos os elementos de para o qual existe um aos quais está relacionados com, e que se caracteriza pela propriedade . Operações teóricas de conjuntos, como a interseção de dois conjuntos, correspondem diretamente à conjunção de predicados. Na lógica categórica , um subcampo da teoria de topos , os quantificadores são identificados com adjuntos ao functor de pullback. Tal realização pode ser vista em analogia à discussão da lógica proposicional usando a teoria dos conjuntos, mas a definição geral contribui para uma gama mais rica de lógicas.
- Portanto, considere um objeto em uma categoria com retrocessos. Qualquer morfismo induz um functor
- na categoria que é a pré-ordem dos subobjetos. Ele mapeia os subobjetos de (tecnicamente: classes de monomorfismo de ) para o retrocesso . Se este functor tiver um adjunto à esquerda ou à direita, eles serão chamados de e , respectivamente. Ambos mapeiam de volta para . Muito aproximadamente, dado um domínio para quantificar uma relação expressa através de mais, os fecha functor / quantificador em e retorna o subconjunto desse modo especificado de .
- Exemplo : Na categoria de conjuntos e funções, os subobjetos canônicos são o subconjunto (ou melhor, suas injeções canônicas). O recuo de uma injeção de um subconjunto em along é caracterizado como o maior conjunto que conhece tudo sobre a injeção de into . Portanto, acaba sendo (em bijeção com) a imagem inversa .
- Pois , vamos descobrir o adjunto esquerdo, que é definido por meio de
- que aqui significa apenas
- .
- Considere . Nós vemos . Por outro lado, se por um também temos , então claramente . Isso implica . Concluímos que o lado esquerdo do functor imagem inverso é dado pela imagem direta. Aqui está uma caracterização desse resultado, que corresponde mais à interpretação lógica: A imagem de sob é o conjunto completo de 's, tal que não é vazio. Isso funciona porque negligencia exatamente aqueles que estão no complemento de . Então
- Faça uma analogia com a nossa motivação .
- O adjunto direito ao functor de imagem inversa é dado (sem fazer o cálculo aqui) por
- O subconjunto de é caracterizado como o conjunto completo de com a propriedade em que a imagem inversa de em relação a está totalmente contida . Observe como o predicado que determina o conjunto é o mesmo acima, exceto que é substituído por .
- Veja também powerset .
Adjunções por completo
Existem, portanto, numerosos functores e transformações naturais associados a cada adjunção, e apenas uma pequena porção é suficiente para determinar o resto.
Uma adjunção entre as categorias C e D consiste em
- Um functor F : D → C chamado de adjunto esquerdo
- Um functor G : C → D chamou o adjunto certo
- Um isomorfismo natural Φ: hom C ( F -, -) → hom D (-, G -)
- Uma transformação natural ε: FG → 1 C chamada de contagem
- Uma transformação natural η: 1 D → GF chamada de unidade
Uma formulação equivalente, em que X denota qualquer objeto de C e Y denota qualquer objeto de D , é a seguinte:
- Para cada C -morfismo f : FY → X , há um único D -morfismo Φ Y , X ( f ) = g : Y → GX de modo que os diagramas abaixo comutam, e para cada D -morfismo g : Y → GX , há um único C- morfismo Φ −1 Y , X ( g ) = f : FY → X em C de modo que os diagramas abaixo comutam:
A partir dessa afirmação, pode-se recuperar que:
- As transformações ε, η e Φ são relacionadas pelas equações
- As transformações ε, η satisfazem as equações da unidade de contagem
- Cada par ( GX , ε X ) é um morfismo terminal de F a X em C
- Cada par ( FY , η Y ) é um morfismo inicial de Y para G em D
Em particular, as equações acima permitem definir Φ, ε e η em termos de qualquer um dos três. No entanto, os functores adjuntos F e G sozinhos não são em geral suficientes para determinar a adjunção. A equivalência dessas situações é demonstrada a seguir.
Morfismos universais induzem adjunção hom-set
Dado um functor adjunto à direita G : C → D ; no sentido de morfismos iniciais, pode-se construir a adjunção de hom-set induzida executando as seguintes etapas.
- Construa um functor F : D → C e uma transformação natural η.
- Para cada objeto Y em D , escolha um morfismo inicial ( F ( Y ), η Y ) de Y para G , de forma que η Y : Y → G ( F ( Y )). Temos o mapa de F em objetos e a família de morfismos η.
- Para cada f : Y 0 → Y 1 , como ( F ( Y 0 ), η Y 0 ) é um morfismo inicial, então fatorar η Y 1 o f com η Y 0 e obter F ( f ): F ( Y 0 ) → F ( Y 1 ). Este é o mapa de F em morfismos.
- O diagrama de comutação dessa fatoração implica no diagrama de comutação das transformações naturais, então η: 1 D → G o F é uma transformação natural .
- A singularidade dessa fatoração e que G é um functor implica que o mapa de F nos morfismos preserva composições e identidades.
- Construa um isomorfismo natural Φ: hom C ( F -, -) → hom D (-, G -).
- Para cada objeto X em C , cada objeto Y em D , como ( F ( Y ), η Y ) é um morfismo inicial, então Φ Y , X é uma bijeção, onde Φ Y , X ( f : F ( Y ) → X ) = G ( f ) o η Y .
- η é uma transformação natural, G é um functor, então para quaisquer objetos X 0 , X 1 em C , quaisquer objetos Y 0 , Y 1 em D , qualquer x : X 0 → X 1 , qualquer y : Y 1 → Y 0 , temos Φ Y 1 , X 1 ( x o f o F ( y )) = G (x) o G ( f ) o G ( F ( y )) o η Y 1 = G ( x ) o G ( f ) o η Y 0 o y = G ( x ) o Φ Y 0 , X 0 ( f ) o y , e então Φ é natural em ambos os argumentos.
Um argumento semelhante permite construir uma adjunção hom-set a partir dos morfismos terminais para um functor adjunto esquerdo. (A construção que começa com um adjunto direito é ligeiramente mais comum, uma vez que o adjunto direito em muitos pares adjunto é uma inclusão definida trivialmente ou um functor esquecido.)
adjunção de unidade de contagem induz adjunção de hom-set
Dados os functores F : D → C , G : C → D , e uma adjunção de unidade de contagem (ε, η): F G , podemos construir uma adjunção de conjunto hom encontrando a transformação natural Φ: hom C ( F -, -) → hom D (-, G -) nas seguintes etapas:
- Para cada f : FY → X e cada g : Y → GX , defina
- As transformações Φ e Ψ são naturais porque η e ε são naturais.
- Usando, na ordem, que F é um functor, que ε é natural, e a equação de unidade de contagem 1 FY = ε FY o F (η Y ), obtemos
- portanto, ΨΦ é a transformação de identidade.
- Dualmente, usando que G é um functor, que η é natural, e a equação de unidade de contagem 1 GX = G (ε X ) o η GX , obtemos
- portanto, ΦΨ é a transformação de identidade. Assim, Φ é um isomorfismo natural com inverso Φ −1 = Ψ.
A adjunção Hom-set induz todos os itens acima
Dados functores F : D → C , G : C → D , e um adjunção hom-set Φ: hom C ( F -, -) → hom D (-, G -), pode-se construir um adjunção cont-unidade
- ,
que define famílias de morfismos iniciais e terminais, nas seguintes etapas:
- Deixe para cada X em C , onde está o morfismo de identidade.
- Deixe para cada Y em D , onde está o morfismo de identidade.
- O bijectivity e naturalidade de Φ implica que cada ( GX , ε X ) é um terminal de morfismo de F para X em C , e cada ( FY , η Y ) é um morfismo inicial de Y para G em D .
- A naturalidade de Φ implica a naturalidade de ε e η, e as duas fórmulas
- para cada f : FY → X e g : Y → GX (que determinam completamente Φ).
- Substituindo FY por X e η Y = Φ Y , FY (1 FY ) por g na segunda fórmula dá a primeira equação de unidade de contagem
- ,
- e substituindo GX por Y e ε X = Φ −1 GX, X (1 GX ) por f na primeira fórmula dá a segunda equação de unidade de contagem
- .
Propriedades
Existência
Nem todo functor G : C → D admite um adjunto esquerdo. Se C é uma categoria completa , então os functores com adjuntos à esquerda podem ser caracterizados pelo teorema do functor adjunto de Peter J. Freyd : G tem um adjunto esquerdo se e somente se for contínuo e uma certa condição de pequenez for satisfeita: para cada objeto Y de D existe uma família de morfismos
- f i : Y → G ( X i )
onde os índices i vêm de um conjunto I , não de uma classe adequada , de modo que todo morfismo
- h : Y → G ( X )
pode ser escrito como
- h = G ( t ) o f i
para algum i em I e algum morfismo
- t : X i → X em C .
Uma declaração análoga caracteriza esses functores com um adjunto direito.
Um caso especial importante é o das categorias apresentáveis localmente . Se for um functor entre categorias apresentáveis localmente, então
- F tem um adjunto direito se e somente se F preserva pequenos colimites
- F tem um adjunto à esquerda se e somente se F preserva pequenos limites e é um functor acessível
Singularidade
Se o functor F : D → C tem duas adjuntas direitas G e G ′, então G e G ′ são naturalmente isomórficos . O mesmo é verdade para os adjuntos esquerdos.
Inversamente, se F for deixado adjunto a G , e G for naturalmente isomorfo a G ′, então F também será deixado adjunto a G ′. Mais geralmente, se 〈F , G , ε, η〉 é uma adjunção (com unidade de contagem (ε, η)) e
- σ: F → F ′
- τ: G → G ′
são isomorfismos naturais então 〈F ′, G ′, ε ′, η ′〉 é uma adjunção onde
Aqui denota composição vertical de transformações naturais e denota composição horizontal.
Composição
As adjunções podem ser compostas de maneira natural. Especificamente, se 〈F , G , ε, η〉 é uma adjunção entre C e D e 〈F ′, G ′, ε ′, η ′〉 é uma adjunção entre D e E então o functor
é deixado adjacente a
Mais precisamente, há uma adjunção entre F F ' e G' G com unidade e contagem dada respectivamente pelas composições:
Esse novo adjunto é chamado de composição dos dois aditivos dados.
Uma vez que também existe uma maneira natural de definir uma adjunção de identidade entre uma categoria C e ela mesma, pode-se então formar uma categoria cujos objetos são todos categorias pequenas e cujos morfismos são adjuntos.
Limite de preservação
A propriedade mais importante dos adjuntos é sua continuidade: todo functor que possui um adjunto à esquerda (e, portanto, é um adjunto à direita) é contínuo (isto é, comuta com limites no sentido teórico da categoria); todo functor que tem um adjunto à direita (e, portanto, é um adjunto à esquerda) é co - contínuo (ou seja, comuta com colimites ).
Uma vez que muitas construções comuns em matemática são limites ou colimites, isso fornece uma riqueza de informações. Por exemplo:
- aplicar um functor adjunto correto a um produto de objetos produz o produto das imagens;
- aplicar um functor adjunto esquerdo a um coproduto de objetos produz o coproduto das imagens;
- todo functor adjunto à direita entre duas categorias abelianas é exata à esquerda ;
- todo functor adjunto à esquerda entre duas categorias abelianas é exatamente correto .
Aditividade
Se C e D são categorias pré - aditivas e F : D → C é um functor aditivo com um adjunto à direita G : C → D , então G também é um functor aditivo e as bijeções hom-set
são, na verdade, isomorfismos de grupos abelianos. Dualmente, se G é aditivo com um F adjunto à esquerda , então F também é aditivo.
Além disso, se C e D são categorias aditivas (isto é, categorias pré- aditivas com todos os biprodutos finitos ), então qualquer par de functores adjuntos entre eles é automaticamente aditivo.
Relacionamentos
Construções universais
Como afirmado anteriormente, uma adjunção entre as categorias C e D dá origem a uma família de morphisms universais , uma para cada objeto em C e um para cada objeto em D . Por outro lado, se existe um morfismo universal para um functor G : C → D de cada objeto de D , então G tem um adjunto esquerdo.
No entanto, as construções universais são mais gerais do que os functores adjuntos: uma construção universal é como um problema de otimização; ele dá origem a um par adjacente se e somente se esse problema tiver uma solução para todos os objetos de D (equivalentemente, todos os objetos de C ).
Equivalências de categorias
Se um functor F : D → C é a metade de uma equivalência de categorias, então ele é o adjunto esquerdo em uma equivalência adjunto de categorias, ou seja, uma adjunção cuja unidade e contagem são isomorfismos.
Cada adjunção 〈F , G , ε, η〉 estende uma equivalência de certas subcategorias. Defina C 1 como a subcategoria completa de C consistindo daqueles objetos X de C para os quais ε X é um isomorfismo, e defina D 1 como a subcategoria completa de D consistindo daqueles objetos Y de D para os quais η Y é um isomorfismo. Então F e G podem ser restritos a D 1 e C 1 e produzir equivalências inversas dessas subcategorias.
Em certo sentido, então, os adjuntos são inversos "generalizados". Nota, contudo, que uma certa inverso de M (ou seja, um functor L de tal modo que FG é naturalmente isomorfo a 1 D ) não precisa de ser um adjunto da direita (esquerda ou para a) F . Adjoints generalizam inversos de dois lados .
Mônadas
Cada adjunção < F , G , ε, η> dá origem a uma associada mônada < T , η, μ> na categoria D . O functor
é dado por T = GF . A unidade da mônada
é apenas a unidade η da adjunção e da transformação de multiplicação
é dada por μ = L ε F . Dualmente, o triplo < FG , ε, F η G > define um comonad em C .
Cada mônada surge de algum complemento - na verdade, normalmente de muitos complementos - da maneira acima. Duas construções, chamadas de categoria de álgebras de Eilenberg-Moore e de categoria de Kleisli, são duas soluções extremas para o problema de construção de uma adjunção que dá origem a uma determinada mônada.
Notas
Referências
- Adámek, Jiří; Herrlich, Horst; Strecker, George E. (1990). Categorias abstratas e concretas. A alegria dos gatos (PDF) . John Wiley & Sons. ISBN 0-471-60922-6. Zbl 0695.18001 .
- Mac Lane, Saunders (1998). Categorias para o Matemático Operário . Textos de Pós-Graduação em Matemática . 5 (2ª ed.). Springer-Verlag. ISBN 0-387-98403-8. Zbl 0906.18001 .
links externos
- Playlist de adjunções no YouTube - sete palestras curtas sobre adjunções por Eugenia Cheng, do The Catsters
- WildCats é um pacote de teoria de categorias para o Mathematica . Manipulação e visualização de objetos, morfismos , categorias, functores , transformações naturais , propriedades universais .































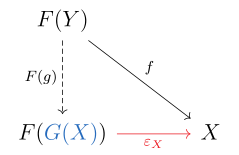


























































![f ^ {{- 1}} [T] \ subseteq X](https://wikimedia.org/api/rest_v1/media/math/render/svg/4a55cb02881c04c713a24cbe82ece550243ab558)


![\ existe _ {f} S \ subseteq T \ leftrightarrow S \ subseteq f ^ {- 1} [T]](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c821337e6e35974fb9c9d1977c1a3b5da169aab)
![f [S] \ subseteq T](https://wikimedia.org/api/rest_v1/media/math/render/svg/6b5dbaa58a61b4955053e8d30ee59bfe257e6c4c)
![S \ subseteq f ^ {{- 1}} [f [S]] \ subseteq f ^ {{- 1}} [T]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c2845f7f5ca6c49df476c5de6e8c4c4385f1539)

![x \ in f ^ {{- 1}} [T]](https://wikimedia.org/api/rest_v1/media/math/render/svg/43e43732bf6ed7b2b03201f6bbb1eea85f573f74)

![S \ subseteq f ^ {- 1} [T]](https://wikimedia.org/api/rest_v1/media/math/render/svg/bad773de89f2d30a93a8442ac7c86eb44e8980bd)


![f ^ {- 1} [\ {y \}] \ cap S](https://wikimedia.org/api/rest_v1/media/math/render/svg/872d2d997b54463e913e7ea72920cfe094e89342)

![f [S]](https://wikimedia.org/api/rest_v1/media/math/render/svg/dc136e58f23572a4001b784eea645e59b735ce49)
![\ existe _ {f} S = \ {y \ em Y \ mid \ existe (x \ em f ^ {- 1} [\ {y \}]). \, x \ em S \; \} = f [ S].](https://wikimedia.org/api/rest_v1/media/math/render/svg/24265e6a1e4e9b58e13a76ba7662185d2527e460)
![\ forall _ {f} S = \ {y \ in Y \ mid \ forall (x \ in f ^ {- 1} [\ {y \}]). \, x \ in S \; \}.](https://wikimedia.org/api/rest_v1/media/math/render/svg/a92d205846301c35cf45cd5cf9e17c4fd5937bd3)



























