Grupos de pontos em quatro dimensões - Point groups in four dimensions

Uma hierarquia de grupos de pontos policóricos 4D e alguns subgrupos. O posicionamento vertical é agrupado por ordem. As cores azul, verde e rosa mostram grupos refletivos, híbridos e rotacionais.

Alguns grupos de pontos 4D na notação de Conway

Em geometria , um grupo de pontos em quatro dimensões é um grupo de isometria em quatro dimensões que deixa a origem fixa, ou correspondentemente, um grupo de isometria de uma 3-esfera .

História em grupos quadridimensionais

1889 Édouard Goursat , Sur les substitutions orthogonales et les divisions régulières de l'espace , Annales Scientifiques de l'École Normale Supérieure, Sér. 3, 6, (pp. 9–102, pp. 80–81 tetraedro), Goursat tetrahedron
1951, AC Hurley, grupos de rotação finita e classes de cristal em quatro dimensões , Proceedings of the Cambridge Philosophical Society, vol. 47, edição 04, p. 650
1962 AL MacKay Bravais Lattices no espaço quadridimensional
1964 Patrick du Val , Homographies, quaternions and rotations , grupos de pontos 4D baseados em quaternion
1975 Jan Mozrzymas, Andrzej Solecki, grupos de pontos R4 , Reports on Mathematical Physics, Volume 7, Issue 3, p. 363-394
1978 H. Brown, R. Bülow, J. Neubüser, H. Wondratschek e H. Zassenhaus, Crystallographic Groups of Four-Dimensional Space.
1982 NP Warner, Os grupos de simetria das tesselações regulares de S2 e S3
1985 EJW Whittaker, Um atlas de hipertereogramas das classes de cristal de quatro dimensões
1985 HSM Coxeter , Regular and Semi-Regular Polytopes II , notação de Coxeter para grupos de pontos 4D
2003 John Conway e Smith, On Quaternions and Octonions , Completed quaternion- based 4D point groups
2018 NW Johnson Geometries and Transformations , Capítulo 11,12,13, Full polychoric groups, p. 249, grupos duoprismáticos p. 269

Isometrias de simetria de ponto 4D

Existem quatro isometrias básicas de simetria de ponto quadridimensional : simetria de reflexão , simetria rotacional , rotorreflecção e rotação dupla .

Notação para grupos

Os grupos de pontos neste artigo são fornecidos na notação de Coxeter , que se baseia em grupos de Coxeter , com marcações para grupos e subgrupos estendidos. A notação de Coxeter tem uma correspondência direta com o diagrama de Coxeter como [3,3,3], [4,3,3], [3 ^1,1,1 ], [3,4,3], [5,3,3] e [p, 2, q]. Esses grupos ligam a esfera 3 em domínios tetraédricos hiperesféricos idênticos. O número de domínios é a ordem do grupo. O número de espelhos para um grupo irredutível é nh / 2 , onde h é o número de Coxeter do grupo de Coxeter , n é a dimensão (4).

Para referência cruzada, também são fornecidas aqui as notações baseadas em quatérnios de Patrick du Val (1964) e John Conway (2003). A notação de Conway permite que a ordem do grupo seja calculada como um produto de elementos com ordens de grupos poliédricos quirais: (T = 12, O = 24, I = 60). Na notação de Conway, um prefixo (±) implica inversão central e um sufixo (.2) implica simetria de espelho. Da mesma forma, a notação de Du Val tem um asterisco (*) sobrescrito para simetria de espelho.

Grupos de involução

Existem cinco grupos involucionais : sem simetria [] ⁺ , simetria de reflexão [], simetria rotacional de 2 vezes [2] ⁺ , rotorreflecção de 2 vezes [2 ⁺ , 2 ⁺ ] e simetria de ponto central [2 ⁺ , 2 ⁺ , 2 ⁺ ] como uma rotação dupla de 2 vezes .

Classificação 4 dos grupos de Coxeter

Um grupo policórico é um dos cinco grupos de simetria dos politopos regulares quadridimensionais . Existem também três grupos prismáticos poliédricos e um conjunto infinito de grupos duoprismáticos. Cada grupo é definido por um domínio fundamental do tetraedro de Goursat delimitado por planos espelhados. Os ângulos diédricos entre os espelhos determinam a ordem de simetria diédrica . O diagrama de Coxeter-Dynkin é um gráfico em que os nós representam planos espelhados e as arestas são chamadas de ramificações e rotuladas por sua ordem de ângulo diedro entre os espelhos.

O termo polychoron (plural polychora , adjetivo policórico ), das raízes gregas poli ("muitos") e choros ("quarto" ou "espaço") e é defendido por Norman Johnson e George Olshevsky no contexto de polychora uniforme (4- politopos) e seus grupos de simetria quadridimensionais relacionados.

Subgrupos ortogonais
B ₄ pode ser decomposto em 2 grupos ortogonais, 4 A ₁ e D ₄ : = (4 espelhos ortogonais) = (12 espelhos)
F ₄ pode ser decomposto em 2 grupos ortogonais D ₄ : = (12 espelhos) = (12 espelhos)
B ₃ × A ₁ pode ser decomposto em grupos ortogonais, 4 A ₁ e D ₃ : = (3 + 1 espelhos ortogonais) = (6 espelhos)

Os grupos de Coxeter de grau 4 permitem que um conjunto de 4 espelhos ocupe o espaço 4 e divide a esfera 3 em domínios fundamentais tetraédricos. Grupos de Coxeter de classificação inferior só podem ligar hosoedro ou domínios fundamentais de hosótopo na 3-esfera.

Como os grupos poliédricos 3D , os nomes dos grupos policóricos 4D dados são construídos pelos prefixos gregos das contagens de células dos politopos regulares com faces triangulares correspondentes. Existem simetrias estendidas em polychora uniforme com padrões de anéis simétricos dentro da construção do diagrama de Coxeter . Existem simetrias quirais em policora uniformes alternadas .

Apenas grupos irredutíveis têm números de Coxeter, mas os grupos duoprismáticos [p, 2, p] podem ser dobrados para [[p, 2, p]] adicionando uma rotação de 2 vezes ao domínio fundamental, e isso dá um número de Coxeter efetivo de 2 p , por exemplo o grupo [4,2,4] e sua simetria completa B ₄ , [4,3,3] com o número de Coxeter 8.

Grupo Weyl	Quaternion de Conway	Estrutura abstrata	Notação de Coxeter	Ordem	Subgrupo comutador	Número de Coxeter (h)	Espelhos (m)
Grupos policóricos completos
A ₄	+ ¹ / ₆₀ [I x I] 0,2 ₁	S ₅	[3,3,3]	120	[3,3,3] ⁺	5		10
D ₄	± 1/3 [T × T] .2	1/2. ² S ₄	[3 ^1,1,1 ]	192	[3 ^1,1,1 ] ⁺	6		12
B ₄	± 1/6 [O × O] .2	² S ₄ = S ₂ ≀S ₄	[4,3,3]	384	[3 ^1,1,1 ] ⁺	8	4	12
F ₄	± 1/2 [O × O] .2 ₃	3. ² S ₄	[3,4,3]	1152	[3 ⁺ , 4,3 ⁺ ]	12	12	12
H ₄	± [I × I] .2	2. (A ₅ × A ₅ ) .2	[5,3,3]	14400	[5,3,3] ⁺	30		60
Grupos prismáticos poliédricos completos
A ₃ A ₁	+1/24 [O × O] .2 ₃	S ₄ × D ₁	[3,3,2] = [3,3] × []	48	[3,3] ⁺	-		6	1
B ₃ A ₁	± 1/24 [O × O] .2	S ₄ × D ₁	[4,3,2] = [4,3] × []	96	[3,3] ⁺	-	3	6	1
H ₃ A ₁	± 1/60 [I × I] .2	A ₅ × D ₁	[5,3,2] = [5,3] × []	240	[5,3] ⁺	-		15	1
Grupos duoprismáticos completos
4A ₁ = 2D ₂	± 1/2 [D ₄ × D ₄ ]	D ₁⁴ = D ₂²	[2,2,2] = [] ⁴ = [2] ²	16	[] ⁺	4	1	1	1	1
D ₂ B ₂	± 1/2 [D ₄ × D ₈ ]	D ₂ × D ₄	[2,2,4] = [2] × [4]	32	[2] ⁺	-	1	1	2	2
D ₂ A ₂	± 1/2 [D ₄ × D ₆ ]	D ₂ × D ₃	[2,2,3] = [2] × [3]	24	[3] ⁺	-	1	1	3
D ₂ G ₂	± 1/2 [D ₄ × D ₁₂ ]	D ₂ × D ₆	[2,2,6] = [2] × [6]	48	[3] ⁺	-	1	1	3	3
D ₂ H ₂	± 1/2 [D ₄ × D ₁₀ ]	D ₂ × D ₅	[2,2,5] = [2] × [5]	40	[5] ⁺	-	1	1	5
2B ₂	± 1/2 [D ₈ × D ₈ ]	D ₄²	[4,2,4] = [4] ²	64	[2 ⁺ , 2,2 ⁺ ]	8	2	2	2	2
B ₂ A ₂	± 1/2 [D ₈ × D ₆ ]	D ₄ × D ₃	[4,2,3] = [4] × [3]	48	[2 ⁺ , 2,3 ⁺ ]	-	2	2	3
B ₂ G ₂	± 1/2 [D ₈ × D ₁₂ ]	D ₄ × D ₆	[4,2,6] = [4] × [6]	96	[2 ⁺ , 2,3 ⁺ ]	-	2	2	3	3
B ₂ H ₂	± 1/2 [D ₈ × D ₁₀ ]	D ₄ × D ₅	[4,2,5] = [4] × [5]	80	[2 ⁺ , 2,5 ⁺ ]	-	2	2	5
2A ₂	± 1/2 [D ₆ × D ₆ ]	D ₃²	[3,2,3] = [3] ²	36	[3 ⁺ , 2,3 ⁺ ]	6	3		3
A ₂ G ₂	± 1/2 [D ₆ × D ₁₂ ]	D ₃ × D ₆	[3,2,6] = [3] × [6]	72		-	3		3	3
2G ₂	± 1/2 [D ₁₂ × D ₁₂ ]	D ₆²	[6,2,6] = [6] ²	144		12	3	3	3	3
A ₂ H ₂	± 1/2 [D ₆ × D ₁₀ ]	D ₃ × D ₅	[3,2,5] = [3] × [5]	60	[3 ⁺ , 2,5 ⁺ ]	-	3		5
G ₂ H ₂	± 1/2 [D ₁₂ × D ₁₀ ]	D ₆ × D ₅	[6,2,5] = [6] × [5]	120	[3 ⁺ , 2,5 ⁺ ]	-	3	3	5
2H ₂	± 1/2 [D ₁₀ × D ₁₀ ]	D ₅²	[5,2,5] = [5] ²	100	[5 ⁺ , 2,5 ⁺ ]	10	5		5
Em geral, p, q = 2,3,4 ...
2I ₂ (2p)	± 1/2 [D _4p × D _4p ]	D _2p²	[2p, 2,2p] = [2p] ²	16p ²	[p ⁺ , 2, p ⁺ ]	2p	p	p	p	p
2I ₂ (p)	± 1/2 [D _2p × D _2p ]	D _p²	[p, 2, p] = [p] ²	4p ²	[p ⁺ , 2, p ⁺ ]	2p	p		p
I ₂ (p) I ₂ (q)	± 1/2 [D _4p × D _4q ]	D _2p × D _2q	[2p, 2,2q] = [2p] × [2q]	16pq	[p ⁺ , 2, q ⁺ ]	-	p	p	q	q
I ₂ (p) I ₂ (q)	± 1/2 [D _2p × D _2q ]	D _p × D _q	[p, 2, q] = [p] × [q]	4pq	[p ⁺ , 2, q ⁺ ]	-	p		q

A ordem de simetria é igual ao número de células do policoro regular vezes a simetria de suas células. O omnitruncated dual polychora tem células que correspondem aos domínios fundamentais do grupo de simetria.

Redes para 4 politopos regulares convexos e duais omnitruncados
Simetria	A ₄	D ₄	B ₄	F ₄	H ₄
4 politopo	5 células	demitesseract	tesserato	24 células	120 células
Células	5 {3,3}	16 {3,3}	8 {4,3}	24 {3,4}	120 {5,3}
Simetria celular	[3,3], pedido 24		[4,3], pedido 48		[5,3], pedido 120
Diagrama de Coxeter		=
Rede de 4 politopos
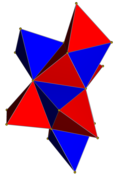
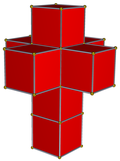
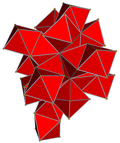
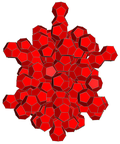
Omnitruncation	omni. 5 células	omni. demitesseract	omni. tesserato	omni. 24 células	omni. 120 células
Omnitruncation dupla net
Diagrama de Coxeter
Células	5 × 24 = 120	(16/2) × 24 = 192	8 × 48 = 384	24 × 48 = 1152	120 × 120 = 14400

Subgrupos quirais

As arestas de 16 células projetadas em uma esfera 3 representam 6 grandes círculos de simetria B4. 3 círculos se encontram em cada vértice. Cada círculo representa eixos de simetria de 4 vezes.

As bordas de 24 células projetadas em uma esfera 3 representam os 16 grandes círculos de simetria F4. Quatro círculos se encontram em cada vértice. Cada círculo representa eixos de simetria tripla.

As bordas de 600 células projetadas em uma esfera 3 representam 72 grandes círculos de simetria H4. Seis círculos se encontram em cada vértice. Cada círculo representa eixos de simetria de 5 vezes.

Os subgrupos diretos dos grupos de pontos reflexivos quadridimensionais são:

Notação de Coxeter		Quaternion de Conway	Estrutura	Ordem	Eixos giratórios
Grupos policóricos
	[3,3,3] ⁺	+1/60 [I × I ]	A ₅	60			10 ₃	10 ₂
	[[3,3,3]] ⁺	± 1/60 [I × I ]	A ₅ × Z ₂	120			10 ₃	(10+?) ₂
	[3 ^1,1,1 ] ⁺	± 1/3 [T × T]	1/2. ² A ₄	96			16 ₃	18 ₂
	[4,3,3] ⁺	± 1/6 [O × O]	² A ₄ = A ₂ ≀A ₄	192	6 ₄		16 ₃	36 ₂
	[3,4,3] ⁺	± 1/2 [O × O]	3. ² A ₄	576	18 ₄	16 ₃	16 ₃	72 ₂
	[3 ⁺ , 4,3 ⁺ ]	± [T × T]		288		16 ₃	16 ₃	(72 + 18) ₂
	[[3 ⁺ , 4,3 ⁺ ]]	± [O × T]		576			32 ₃	(72 + 18 +?) ₂
	[[3,4,3]] ⁺	± [O × O]		1152	18 ₄		32 ₃	(72+?) ₂
	[5,3,3] ⁺	± [I × I]	2. (A ₅ × A ₅ )	7200		72 ₅	200 ₃	450 ₂
Grupos prismáticos poliédricos
	[3,3,2] ⁺	+ ¹ / _{24 de} [S x S ]	A ₄ × Z ₂	24		4 ₃	4 ₃	(6 + 6) ₂
	[4,3,2] ⁺	± 1/24 [O × O]	S ₄ × Z ₂	48		6 ₄	8 ₃	(3 + 6 + 12) ₂
	[5,3,2] ⁺	± 1/60 [I × I]	A ₅ × Z ₂	120		12 ₅	20 ₃	(15 + 30) ₂
Grupos duoprismáticos
	[2,2,2] ⁺	+1/2 [D ₄ × D ₄ ]		8		1 ₂	1 ₂	4 ₂
	[3,2,3] ⁺	+1/2 [D ₆ × D ₆ ]		18		1 ₃	1 ₃	9 ₂
	[4,2,4] ⁺	+1/2 [D ₈ × D ₈ ]		32		1 ₄	1 ₄	16 ₂
(p, q = 2,3,4 ...), mdc (p, q) = 1
	[p, 2, p] ⁺	+1/2 [D _2p × D _2p ]		2p ²		1 _p	1 _p	(pp) ₂
	[p, 2, q] ⁺	+1/2 [D _2p × D _2q ]		2pq		1 _p	1 _q	(pq) ₂
	[p ⁺ , 2, q ⁺ ]	+ [C _p × C _q ]	Z _p × Z _q	pq		1 _p	1 _q

Simetria pentacórica

Grupo pentacórico - A ₄ , [3,3,3], ( ), A ordem 120, (Du Val # 51' (I ^† / C ₁ ; E / C ₁ ) ^{† *} , Conway + ¹ / ₆₀ [I x I] 0,2 ₁ ), chamado para o 5-célula (pentachoron) , dado pelo diagrama de Coxeter anelado . Às vezes também é chamado de grupo hiper-tetraédrico para estender o grupo tetraédrico [3,3]. Existem 10 hiperplanos de espelho neste grupo. É isomórfico ao grupo simétrico abstrato , S ₅
.
- O grupo pentacórico estendido , Aut ( A ₄ ), [[3,3,3]], (A duplicação pode ser sugerida por um diagrama dobrado, ), A ordem 240, (Du Val # 51 (I ^{† *} / C ₂ ; I / C ₂ ) ^{† *} , Conway ± ¹ / ₆₀ [I x I ] 0,2). É isomórfico ao produto direto de grupos abstratos: S ₅ × C ₂ .
  - O grupo pentacórico estendido quiral é [[3,3,3]] ⁺ , ( ), A ordem 120, (Du Val # 32 (I ^† / C ₂ ; I / C ₂ ) ^† , Conway ± ¹ / ₆₀ [Ix I ]). Este grupo representa a construção da célula 5 omnisnub , , embora não possa ser uniformizado. É isomórfico ao produto direto de grupos abstratos: A ₅ × C ₂ .
- O grupo pentacórico quiral é [3,3,3] ⁺ , ( ), A ordem de 60, (Du Val # 32' (I ^† / C ₁ ; E / C ₁ ) ^† , Conway + ¹ / ₆₀ [I x I ]). É isomórfico ao
grupo alternado abstrato , A ₅
.
- O grupo pentachoric quiral estendida é [[3,3,3] ⁺ ], a ordem 120, (Du Val # 51" (I ^† / C ₁ ; E / C ₁ ) _-^{† *} , Conway + ¹ / ₆₀ [ixi] .2 ₃ ). Coxeter relaciona este grupo ao grupo abstrato (4,6 | 2,3). Também é isomórfico ao
grupo simétrico abstrato , S ₅ .

Simetria hexadecacórica

Grupo hexadecacórico - B ₄ , [4,3,3], ( ), A ordem 384, (Du Val # 47 (S / V; S / V) ^* , Conway ± ¹ / ₆ [O × O] 0,2), com o nome do 16-célula (hexadecachoron), . Existem 16 hiperplanos de espelho neste grupo, que podem ser identificados em 2 conjuntos ortogonais: 12 de um subgrupo [3 ^1,1,1 ] e 4 de um subgrupo [2,2,2]. É também chamado de grupo hiper-octaédrico para estender o grupo octaédrico 3D [4,3], e o grupo tesserático para o tesserato , .
- O grupo hexadecacórico quiral é [4,3,3] ⁺ , ( ), A ordem 192, (Du Val # 27 (S / V; S / V), Conway ± ¹ / ₆ [O × O]). Este grupo representa a construção de um tesserato omnisnub , , embora não possa ser uniformizado.
- O grupo hexadecacórico iônico diminuído é [4, (3,3) ⁺ ], ( ), A ordem 192, (Du Val # 41 (t / V; t / V) ^* , Conway ± ¹ / ₃ [T × T] 0,2). Este grupo leva ao snub de 24 células com construção .
- O grupo meio hexadecacórico é [1 ⁺ , 4,3,3], ( = ), ordem 192, e mesmo que a simetria #demitesserática : [3 ^1,1,1 ]. Este grupo é expresso na construção alternada do tesserato das 16 células
  , = .
  - O grupo [1 ⁺ , 4, (3,3) ⁺ ], ( = ), ordem 96, e mesmo que o grupo quiral desmitesserático [3 ^1,1,1 ] ⁺ e também é o subgrupo comutador de [4,3,3].
- Um subgrupo reflexivo de alto índice é a simetria octaédrica prismática , [4,3,2] ( ), A ordem de 96, o índice de subgrupo 4, (Du Val # 44 (S / C ₂ ; O / C ₂ ) ^* , Conway ± ¹ / _{24 de} [ó x O] 0,2). O prisma cúbico truncado tem esta simetria com o diagrama de Coxeter e o prisma cúbico é uma construção de simetria inferior do tesserato , como .
  - Seu subgrupo quiral é [4,3,2] ⁺ , ( ), A ordem de 48, (Du Val # 26 (S / C ₂ ; O / C ₂ ), Conway ± ¹ / _{24 de} [ó x O]). Um exemplo é o antiprisma cúbico esnobe , , embora não possa ser uniformizado.
  - Os subgrupos iônicos são:
    - [(3,4) ⁺ , 2], ( ), A ordem de 48, (Du Val # 44b'(S / C ₁ ; S / C ₁ ) _-^* , Conway + ¹ / _{24 de} [ó x O] 0,2 ₁ ). O prisma cúbico snub tem esta simetria com o diagrama de Coxeter .
      - [(3,4) ⁺ , 2 ⁺ ], ( ), A ordem de 24, (Du Val # 44' (T / C ₂ ; T / C ₂ ) _-^* , Conway + ¹ / ₁₂ [T × T] 0,2 ₁ ).
    - [4,3 ⁺ , 2], ( ), A ordem de 48, (Du Val # 39 (T / C ₂ ; T / C ₂ ) _c^* , Conway ± ¹ / ₁₂ [T × T] 0,2).
      - [4,3 ⁺ , 2,1 ⁺ ] = [4,3 ⁺ , 1] = [4,3 ⁺ ], ( = ), A ordem de 24, (Du Val # 44" (T / C ₂ ; T / C ₂ ) ^* , Conway + ¹ / ₁₂ [T × T] 0,2 ₃ ) Este é o 3D. Grupo pyritohedral , [4,3 ⁺ ].
      - [3 ⁺ , 4,2 ⁺ ], ( ), A ordem de 24, (Du Val # 21 (T / C ₂ ; T / C ₂ ), Conway ± ¹ / ₁₂ [T × T]).
    - [3,4,2 ⁺ ], ( ), A ordem de 48, (Du Val # 39' (T / C ₂ ; T / C ₂ ) _-^* , Conway ± ¹ / ₁₂ [T × T ] 0,2).
    - [4, (3,2) ⁺ ], ( ), A ordem de 48, (Du Val # 40b'(S / C ₁ ; S / C ₁ ) _-^* , Conway + ¹ / _{24 de} [S x S ] 0,2 ₁ ).
  - Um meio subgrupo [4,3,2,1 ⁺ ] = [4,3,1] = [4,3], ( = ), A fim 48 (Du Val # 44b"(O / C ₁ ; S / C ₁ ) _c^* , Conway + ¹ / _{24 de} [ó x O] 0,2 ₃ ). Chama-se o grupo octaédrico piramidal e é 3D octaédrica simetria , [4,3]. Uma pirâmide cúbica pode ter esta simetria, com o símbolo de Schläfli : () ∨ {4,3}.
    
    [4,3], , o grupo piramidal octaédrico é isomórfico a simetria octaédrica 3d
    - Um meio subgrupo quiral [(4,3) ⁺ , 2,1 ⁺ ] = [4,3,1] ⁺ = [4,3] ⁺ , ( = ), A fim 24 (Du Val # 26b'(S / C ₁ ; S / C ₁ ), Conway + ¹ / ₂₄ [S x S]). Este é o grupo octaédrico quiral 3D , [4,3] ⁺ . Uma pirâmide cúbica desprezível pode ter esta simetria, com o símbolo de Schläfli: () ∨ sr {4,3}.
- Outro subgrupo reflexivo de alto índice é a simetria tetraédrica prismática , [3,3,2], ( ), A ordem de 48, o índice do subgrupo 8, (Du Val # 40b"(O / C ₁ ; S / C ₁ ) ^* , Conway + ¹ / _{24 de} [S x S ] 0,2 ₃ ).
  - O subgrupo quiral é [3,3,2] ⁺ , ( ), A ordem de 24, (Du Val # 26b"(O / C ₁ ; S / C ₁ ), Conway + ¹ / ₂₄ [S x S .]) Um exemplo é o achatado tetraédrico antiprisma , , embora não possa ser uniformizado.
  - O subgrupo iônico é [(3,3) ⁺ , 2], ( ), A ordem de 24, (Du Val # 39b'(T / C ₁ ; T / C ₁ ) _c^* , Conway + ¹ / ₁₂ [T × T ] 0,2 ₃ ). Um exemplo é o prisma tetraédrico snub , .
  - O meio subgrupo é [3,3,2,1 ⁺ ] = [3,3,1] = [3,3], ( = ), A ordem de 24, (Du Val # 39b"(T / C ₁ ; T / C ₁ ) _-^* , Conway + ¹ / ₁₂ [T × T ] 0,2 ₁ ). Chama-se o grupo tetraédrico piramidal e é a Grupo tetraédrico 3D , [3,3]. Uma pirâmide tetraédrica regular pode ter esta simetria, com o símbolo de Schläfli: () ∨ {3,3}.
    
    [3,3], , o grupo piramidal tetraédrico é isomórfico a simetria tetraédrica 3d
    - O meio subgrupo quiral [(3,3) ⁺ , 2,1 ⁺ ] = [3,3] ⁺ ( = ), A ordem de 12, (Du Val # 21b'(T / C ₁ ; T / C ₁ ), Conway + ¹ / ₁₂ [T × T]). Este é o grupo tetraédrico quiral 3D , [3,3] ⁺ . Uma pirâmide tetraédrica desprezível pode ter esta simetria, com o símbolo de Schläfli: () ∨ sr {3,3}.
- Outro subgrupo reflexivo radial de alto índice é [4, (3,3) ^* ], índice 24, remove espelhos com ângulos diédricos de ordem 3, criando [2,2,2] ( ), pedido 16. Outros são [4,2,4] ( ), [4,2,2] ( ), com índices de subgrupo 6 e 12, ordem 64 e 32. Esses grupos são simetrias inferiores do tesserato : ( ), ( ), e ( ) Esses grupos são # simetria duoprismática .

Simetria icossitetracórica

Grupo icossitetracórico - F ₄ , [3,4,3], ( ), A ordem de 1152, (Du Val # 45 (S / T; S / T) ^* , Conway ± ¹ / ₂ [OxO] 0,2), com o nome do 24-célula (icositetrachoron), . Existem 24 planos de espelho nesta simetria, que podem ser decompostos em dois conjuntos ortogonais de 12 espelhos em subgrupos de simetria demitesserática [3 ^1,1,1 ], como [3 ^* , 4,3] e [3,4,3 ^* ], como índice de 6 subgrupos.
- O grupo icositetracórico estendido , Aut ( F ₄ ), [[3,4,3]], ( ) tem ordem 2304, (Du Val # 48 (O / O; O / O) ^* , Conway ± [O × O] .2).
  - O grupo icositetracórico quiral estendido , [[3,4,3]] ⁺ , ( ) tem a ordem 1152, (Du Val # 25 (O / O; O / O), Conway ± [OxO]). Este grupo representa a construção da omnisnub de 24 células , , embora não possa ser uniformizado.
- Os grupos icositetracóricos iônicos diminuídos , [3 ⁺ , 4,3] e [3,4,3 ⁺ ], ( ou ), tem ordem 576, (Du Val # 43 (T / T; T / T) ^* , Conway ± [T × T] .2). Este grupo leva ao snub de 24 células com construção ou .
  - O grupo icositetracórico duplo diminuído , [3 ⁺ , 4,3 ⁺ ] (a diminuição dupla pode ser mostrada por uma lacuna no diagrama de 4 ramos: ), ordem 288, (Du Val # 20 (T / T; T / T), Conway ± [T × T]) é o subgrupo do comutador
    de [3,4,3].
    - Pode ser estendido como [[3 ⁺ , 4,3 ⁺ ]], ( ) pedido 576, (Du Val # 23 (T / T; O / O), Conway ± [OxT]).
- O grupo quiral icositetracórico é [3,4,3] ⁺ , ( ), A ordem 576, (Du Val # 28 (S / T; S / T), Conway ± ¹ / ₂ [S x S]).
  - O grupo icositetrachoric quiral estendida , [[3,4,3] ⁺ ] tem ordem de 1152, (Du Val # 46 (S / T; S / T) _-^* , Conway ± ¹ / ₂ [OxO]. 2 ). Coxeter relaciona este grupo ao grupo abstrato (4,8 | 2,3).

Simetria demitesserática

Grupo semisserático - D ₄ , [3 ^1,1,1 ], [3,3 ^1,1 ] ou [3,3,4,1 ⁺ ], ( = ), A ordem 192, (Du Val # 42 (t / V; t / V) _-^* , Conway ± ¹ / ₃ [T × T ] 0,2), com o nome do (demitesseract) 4-demicube construção da 16- célula, ou . Existem 12 espelhos neste grupo de simetria.
- Existem dois tipos de simetrias estendidas pela adição de espelhos: <[3,3 ^1,1 ]> que se torna [4,3,3] pela bissetriz do domínio fundamental por um espelho, com 3 orientações possíveis; e o grupo estendido completo [3 [3 ^1,1,1 ]] torna-se [3,4,3].
- O grupo quiral desmitesserático é [3 ^1,1,1 ] ⁺ ou [1 ⁺ , 4, (3,3) ⁺ ], ( = ), A ordem de 96, (Du Val # 22 (t / V; t / V), Conway ± ¹ / ₃ [T × T]). Este grupo leva ao snub de 24 células com construção = .

Simetria hexacosicórica

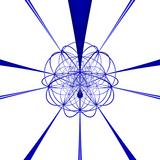[5,3,3] ⁺ 72 ordem-5 giros	[5,3,3] ⁺ 200 giros de ordem 3
[5,3,3] ⁺ 450 giros ordem 2	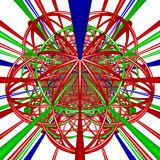[5,3,3] ⁺ todas as girações
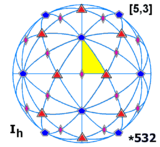[5,3], , o grupo piramidal icosaédrico é isomórfico a simetria icosaédrica 3d

Grupo hexacosicórico - H ₄ , [5,3,3], ( ), ordem 14400, (Du Val # 50 (I / I; I / I) ^* , Conway ± [I × I] .2), nomeado para a célula 600 (hexacosichoron), . Às vezes também é chamado de grupo hiper-icosaédrico para estender o grupo icosaédrico 3D [5,3] e grupo hecatonicosacórico ou grupo dodecacontacórico
das células 120 , .
- O grupo hexacosicórico quiral é [5,3,3] ⁺ , ( ), pedido 7200, (Du Val # 30 (I / I; I / I), Conway ± [I × I]). Este grupo representa a construção da célula 120 snub , , embora não possa ser uniformizado.
- Um subgrupo reflexivo de alto índice é a simetria icosaédrica prismática , [5,3,2], ( ), A fim de 240, índice de subgrupo 60, (Du Val # 49 (I / C ₂ ; I / C ₂ ) ^* , Conway ± ¹ / ₆₀ [ixi] 0,2).
  - Seu subgrupo quiral é [5,3,2] ⁺ , ( ), A ordem 120, (Du Val # 31 (I / C ₂ ; I / C ₂ ), Conway ± ¹ / ₆₀ [ixi]). Este grupo representa a construção do antiprisma dodecaédrico esnobe , , embora não possa ser uniformizado.
  - Um subgrupo iônico é [(5,3) ⁺ , 2], ( ), A ordem 120, (Du Val # 49' (I / C ₁ ; E / C ₁ ) ^* , Conway + ¹ / ₆₀ [ixi] 0,2 ₁ ). Este grupo representa a construção do prisma dodecaédrico snub , .
  - Um meio subgrupo é [5,3,2,1 ⁺ ] = [5,3,1] = [5,3], ( = ), A ordem 120, (Du Val # 49" (I / C ₁ ; E / C ₁ ) _-^* , Conway + ¹ / ₆₀ [ixi] 0,2 ₃ ) Ele é chamado o. Grupo piramidal icosaédrica e é o 3D icosaédrica grupo , [5,3]. Uma pirâmide dodecaédrica regular pode ter esta simetria, com o símbolo de Schläfli : () ∨ {5,3}.
    - Um meio subgrupo quiral é [(5,3) ⁺ , 2,1 ⁺ ] = [5,3,1] ⁺ = [5,3] ⁺ , ( = ), A ordem de 60, (Du Val # 31' (I / C ₁ ; E / C ₁ ), Conway + ¹ / ₆₀ [ixi]). Este é o grupo quiral icosaédrico 3D , [5,3] ⁺ . Uma pirâmide dodecaédrica desprezível pode ter esta simetria, com o símbolo Schläfli : () ∨ sr {5,3}.

Simetria duoprismática

Grupos duoprismáticos - [p, 2, q], ( ), ordem 4 pq , existe para todos 2 ≤ p , q <∞. Existem espelhos p + q nesta simetria, que são trivialmente decompostos em dois conjuntos ortogonais de espelhos peq de simetria diédrica : [p] e [q].
- O subgrupo quiral é [p, 2, p] ⁺ , ( ), peça 2 pq . Pode ser duplicado como [[2p, 2,2p] ⁺ ].
- Se p e q forem iguais, [p, 2, p], ( ), a simetria pode ser duplicada como [[p, 2, p]], ( )
  - Duplicações: [[p ⁺ , 2, p ⁺ ]], ( ), [[2p, 2 ⁺ , 2p]], [[2p ⁺ , 2 ⁺ , 2p ⁺ ]].
- [p, 2, ∞], ( ), representa grupos de linhas em 3 espaços,
- [∞, 2, ∞], ( ) representa a simetria do plano euclidiano com dois conjuntos de espelhos paralelos e um domínio retangular ( orbifold * 2222).
- Os subgrupos incluem: [p ⁺ , 2, q], ( ), [p, 2, q ⁺ ], ( ), [p ⁺ , 2, q ⁺ ], ( )
- E para valores pares: [2p, 2 ⁺ , 2q], ( ), [2p, 2 ⁺ , 2q ⁺ ], ( ), [(p, 2) ⁺ , 2q], ( ), [2p, (2, q) ⁺ ], ( ), [(p, 2) ⁺ , 2q ⁺ ], ( ), [2p ⁺ , (2, q) ⁺ ], ( ), [2p ⁺ , 2 ⁺ , 2q ⁺ ], ( ), e subgrupo de comunicador, índice 16, [2p ⁺ , 2 ⁺ , 2q ⁺ ] ⁺ , ( )
Grupo duoprismático digonal - [2,2,2], ( ), pedido 16.
- O subgrupo quiral é [2,2,2] ⁺ , ( ), pedido 8.
- Estendido [[2,2,2]], ( ), ordem 32. O duoprismo 4-4 tem esta simetria estendida, .
  - O grupo quiral estendido é [[2,2,2]] ⁺ , ordem 16.
  - O subgrupo quiral estendido é [[2,2,2] ⁺ ], ordem 16, com geradores de rotorreflexão . É isomórfico ao grupo abstrato (4,4 | 2,2).
- Outro estendido [(3,3) [2,2,2]] = [4,3,3], ordem 384, # Simetria hexadecacórica . O tesserato tem essa simetria, como ou .
- Os subgrupos diminuídos iônicos são [2 ⁺ , 2,2], ordem 8.
  - O subgrupo duplo diminuído é [2 ⁺ , 2,2 ⁺ ], ordem 4.
    - Estendido como [[2 ⁺ , 2,2 ⁺ ]], ordem 8.
  - Os subgrupos de rotorreflecção são [2 ⁺ , 2 ⁺ , 2], [2,2 ⁺ , 2 ⁺ ], [2 ⁺ , (2,2) ⁺ ], [(2,2) ⁺ , 2 ⁺ ] ordem 4.
  - O subgrupo triplo diminuído é [2 ⁺ , 2 ⁺ , 2 ⁺ ], ( ), ordem 2. É uma rotação dupla de 2 vezes e uma inversão central 4D .
- Meio subgrupo é [1 ⁺ , 2,2,2] = [1,2,2], ordem 8.
Grupo duoprismático triangular
- [3,2,3], , pedido 36.
- O subgrupo quiral é [3,2,3] ⁺ , ordem 18.
- Extended [[3,2,3]], ordem 72. O duoprisma 3-3 tem esta simetria estendida, .
  - O grupo quiral estendido é [[3,2,3]] ⁺ , ordem 36.
  - O subgrupo quiral estendido é [[3,2,3] ⁺ ], ordem 36, com geradores de rotorreflexão . É isomórfico ao grupo abstrato (4,4 | 2,3).
- Outros estendidos [[3], 2,3], [3,2, [3]], ordem 72 e são isomórficos a [6,2,3] e [3,2,6].
- E [[3], 2, [3]], ordem 144, e é isomórfico a [6,2,6].
- E [[[3], 2, [3]]], ordem 288, isomórfico a [[6,2,6]]. O duoprismo 6-6 tem esta simetria, como ou .
- Os subgrupos diminuídos iônicos são [3 ⁺ , 2,3], [3,2,3 ⁺ ], ordem 18.
  - O subgrupo duplo diminuído é [3 ⁺ , 2,3 ⁺ ], ordem 9.
    - Estendido como [[3 ⁺ , 2,3 ⁺ ]], ordem 18.
- Um subgrupo de alto índice é [3,2], ordem 12, índice 3, que é isomórfico à simetria diédrica no grupo de
três dimensões
, [3,2], D _3h .
- [3,2] ⁺ , ordem 6

Grupo duoprismático quadrado - [4,2,4],

, pedido 64.

O subgrupo quiral é [4,2,4] ⁺ , ordem 32.
Extended [[4,2,4]], ordem 128. O duoprismo 4-4 tem esta simetria estendida, .
- O grupo estendido quiral é [[4,2,4]] ⁺ , ordem 64.
- O subgrupo quiral estendido é [[4,2,4] ⁺ ], ordem 64, com geradores de rotorreflexão . É isomórfico ao grupo abstrato (4,4 | 2,4).
Outros estendidos [[4], 2,4], [4,2, [4]], ordem 128 e são isomórficos a [8,2,4] e [4,2,8]. O duoprismo 4-8 tem esta simetria, como ou .
E [[4], 2, [4]], ordem 256 e é isomórfico a [8,2,8].
E [[[4], 2, [4]]], ordem 512, isomórfico a [[8,2,8]]. O duoprismo 8-8 tem esta simetria, como ou .
Os subgrupos diminuídos iônicos são [4 ⁺ , 2,4], [4,2,4 ⁺ ], ordem 32.
- O subgrupo duplo diminuído é [4 ⁺ , 2,4 ⁺ ], ordem 16.
  - Estendido como [[4 ⁺ , 2,4 ⁺ ]], ordem 32.
- Os subgrupos de rotorreflecção são [4 ⁺ , 2 ⁺ , 4], [4,2 ⁺ , 4 ⁺ ], [4 ⁺ , (2,4) ⁺ ], [(4,2) ⁺ , 4 ⁺ ], ( , , , ) pedido 16.
- O subgrupo triplo diminuído é [4 ⁺ , 2 ⁺ , 4 ⁺ ], ( ), pedido 8.
Metade dos subgrupos são [1 ⁺ , 4,2,4] = [2,2,4], ( ), [4,2,4,1 ⁺ ] = [4,2,2], ( ), pedido 32.
- [1 ⁺ , 4,2,4] ⁺ = [2,2,4] ⁺ , ( ), [4,2,4,1 ⁺ ] ⁺ = [4,2,2] ⁺ , ( ), pedido 16.
Metade novamente o subgrupo é [1 ⁺ , 4,2,4,1 ⁺ ] = [2,2,2], ( ), pedido 16.
- [1 ⁺ , 4,2,4,1 ⁺ ] ⁺ = [1 ⁺ , 4,2 ⁺ , 4,1 ⁺ ] = [2,2,2] ⁺ , ( ) pedido 8

Resumo de alguns grupos de pontos quadridimensionais

Este é um resumo dos grupos de pontos quadridimensionais na notação de Coxeter . 227 deles são grupos de pontos cristalográficos (para valores particulares de p e q). (nc) é dado para grupos não cristalográficos. Alguns grupos cristalográficos têm suas ordens indexadas (order.index) por sua estrutura abstrata de grupo.

Grupos finitos

[]:
Símbolo	Ordem
[1] ⁺	1,1
[1] = []	2,1

[2]:
Símbolo	Ordem
[1 ⁺ , 2] ⁺	1,1
[2] ⁺	2,1
[2]	4,1

[2,2]:
Símbolo	Ordem
[2 ⁺ , 2 ⁺ ] ⁺ = [(2 ⁺ , 2 ⁺ , 2 ⁺ )]	1,1
[2 ⁺ , 2 ⁺ ]	2,1
[2,2] ⁺	4,1
[2 ⁺ , 2]	4,1
[2,2]	8,1

[2,2,2]:
Símbolo	Ordem
[(2 ⁺ , 2 ⁺ , 2 ⁺ , 2 ⁺ )] = [2 ⁺ , 2 ⁺ , 2 ⁺ ] ⁺	1,1
[2 ⁺ , 2 ⁺ , 2 ⁺ ]	2,1
[2 ⁺ , 2,2 ⁺ ]	4,1
[(2,2) ⁺ , 2 ⁺ ]	4
[[2 ⁺ , 2 ⁺ , 2 ⁺ ]]	4
[2,2,2] ⁺	8
[2 ⁺ , 2,2]	8,1
[(2,2) ⁺ , 2]	8
[[2 ⁺ , 2,2 ⁺ ]]	8,1
[2,2,2]	16,1
[[2,2,2]] ⁺	16
[[2,2 ⁺ , 2]]	16
[[2,2,2]]	32

[ p ]:
Símbolo	Ordem
[ p ] ⁺	p
[ p ]	2p

[p, 2]:
Símbolo	Ordem
[ p , 2] ⁺	2 p
[ p , 2]	4 p

[2p, 2 ⁺ ]:
Símbolo	Ordem
[2 p , 2 ⁺ ]	4 p
[2 p ⁺ , 2 ⁺ ]	2 p

[ p , 2,2]:
Símbolo	Ordem
[ p ⁺ , 2,2 ⁺ ]	2 p
[( p , 2) ⁺ , 2 ⁺ ]	2 p
[ p , 2,2] ⁺	4 p
[ p , 2,2 ⁺ ]	4 p
[p ⁺ , 2,2]	4 p
[(p, 2) ⁺ , 2]	4 p
[p, 2,2]	8 p

[2 p , 2 ⁺ , 2]:
Símbolo	Ordem
[ 2p ⁺ , 2 ⁺ , 2 ⁺ ] ⁺	p
[ 2p ⁺ , 2 ⁺ , 2 ⁺ ]	2 p
[2 p ⁺ , 2 ⁺ , 2]	4 p
[2 p ⁺ , (2,2) ⁺ ]	4 p
[2 p , (2,2) ⁺ ]	8 p
[2 p , 2 ⁺ , 2]	8 p

[ p , 2, q ]:
Símbolo	Ordem
[ p ⁺ , 2, q ⁺ ]	pq
[ p , 2, q ] ⁺	2 pq
[ p ⁺ , 2, q ]	2 pq
[ p , 2, q ]	4 pq
Símbolo	Ordem
[( p , 2) ⁺ , 2 q ⁺ ]	2 pq
[( p , 2) ⁺ , 2 q ]	4 pq

[2 p , 2,2 q ]:
Símbolo	Ordem
[2 p ⁺ , 2 ⁺ , 2 q ⁺ ] ⁺ = [(2 p ⁺ , 2 ⁺ , 2 q ⁺ , 2 ⁺ )]	pq
[2 p ⁺ , 2 ⁺ , 2 q ⁺ ]	2pq
[2 p , 2 ⁺ , 2 q ⁺ ]	4 pq
[((2 p , 2) ⁺ , (2 q , 2) ⁺ )]	4 pq
[2 p , 2 ⁺ , 2 q ]	8 pq

[[ p , 2, p ]]:
Símbolo	Ordem
[[ p ⁺ , 2, p ⁺ ]]	2 p ²
[[ p , 2, p ]] ⁺	4 p ²
[[ p , 2, p ] ⁺ ]	4 p ²
[[ p , 2, p ]]	8 p ²

[[2 p , 2,2 p ]]:
Símbolo	Ordem
[[(2 p ⁺ , 2 ⁺ , 2 p ⁺ , 2 ⁺ )]]	2 p ²
[[2 p ⁺ , 2 ⁺ , 2 p ⁺ ]]	4 p ²
[[((2 p , 2) ⁺ , (2 p , 2) ⁺ )]]	8 p ²
[[ 2p , 2 ⁺ , 2p ]]	16 p ²

[3,3,2]:
Símbolo	Ordem
[(3,3) ^Δ , 2,1 ⁺ ] ≅ [2,2] ⁺	4
[(3,3) ^Δ , 2] ≅ [2, (2,2) ⁺ ]	8
[(3,3) ^⅄ , 2,1 ⁺ ] ≅ [4,2 ⁺ ]	8
[(3,3) ⁺ , 2,1 ⁺ ] = [3,3] ⁺	12,5
[(3,3) ^⅄ , 2] ≅ [2,4,2 ⁺ ]	16
[3,3,2,1 ⁺ ] = [3,3]	24
[(3,3) ⁺ , 2]	24,10
[3,3,2] ⁺	24,10
[3,3,2]	48,36

[4,3,2]:
Símbolo	Ordem
[1 ⁺ , 4,3 ⁺ , 2,1 ⁺ ] = [3,3] ⁺	12
[3 ⁺ , 4,2 ⁺ ]	24
[(3,4) ⁺ , 2 ⁺ ]	24
[1 ⁺ , 4,3 ⁺ , 2] = [(3,3) ⁺ , 2]	24,10
[3 ⁺ , 4,2,1 ⁺ ] = [3 ⁺ , 4]	24,10
[(4,3) ⁺ , 2,1 ⁺ ] = [4,3] ⁺	24,15
[1 ⁺ , 4,3,2,1 ⁺ ] = [3,3]	24
[1 ⁺ , 4, (3,2) ⁺ ] = [3,3,2] ⁺	24
[3,4,2 ⁺ ]	48
[4,3 ⁺ , 2]	48,22
[4, (3,2) ⁺ ]	48
[(4,3) ⁺ , 2]	48,36
[1 ⁺ , 4,3,2] = [3,3,2]	48,36
[4,3,2,1 ⁺ ] = [4,3]	48,36
[4,3,2] ⁺	48,36
[4,3,2]	96,5

[5,3,2]:
Símbolo	Ordem
[(5,3) ⁺ , 2,1 ⁺ ] = [5,3] ⁺	60,13
[5,3,2,1 ⁺ ] = [5,3]	120,2
[(5,3) ⁺ , 2]	120,2
[5,3,2] ⁺	120,2
[5,3,2]	240 (nc)

[3 ^1,1,1 ]:
Símbolo	Ordem
[3 ^1,1,1 ] ^Δ ≅ [[4,2 ⁺ , 4]] ⁺	32
[3 ^1,1,1 ] ^⅄	64
[3 ^1,1,1 ] ⁺	96,1
[3 ^1,1,1 ]	192,2
<[3,3 ^1,1 ]> = [4,3,3]	384,1
[3 [3 ^1,1,1 ]] = [3,4,3]	1152,1

[3,3,3]:
Símbolo	Ordem
[3,3,3] ⁺	60,13
[3,3,3]	120,1
[[3,3,3]] ⁺	120,2
[[3,3,3] ⁺ ]	120,1
[[3,3,3]]	240,1

[4,3,3]:
Símbolo	Ordem
[1 ⁺ , 4, (3,3) ^Δ ] = [3 ^1,1,1 ] ^Δ ≅ [[4,2 ⁺ , 4]] ⁺	32
[4, (3,3) ^Δ ] = [2 ⁺ , 4 [2,2,2] ⁺ ] ≅ [[4,2 ⁺ , 4]]	64
[1 ⁺ , 4, (3,3) ^⅄ ] = [3 ^1,1,1 ] ^⅄	64
[1 ⁺ , 4, (3,3) ⁺ ] = [3 ^1,1,1 ] ⁺	96,1
[4, (3,3) ^⅄ ] ≅ [[4,2,4]]	128
[1 ⁺ , 4,3,3] = [3 ^1,1,1 ]	192,2
[4, (3,3) ⁺ ]	192,1
[4,3,3] ⁺	192,3
[4,3,3]	384,1

[3,4,3]:
Símbolo	Ordem
[3 ⁺ , 4,3 ⁺ ]	288,1
[3,4,3 ^⅄ ] = [4,3,3]	384,1
[3,4,3] ⁺	576,2
[3 ⁺ , 4,3]	576,1
[[3 ⁺ , 4,3 ⁺ ]]	576 (nc)
[3,4,3]	1152,1
[[3,4,3]] ⁺	1152 (nc)
[[3,4,3] ⁺ ]	1152 (nc)
[[3,4,3]]	2304 (nc)

[5,3,3]:
Símbolo	Ordem
[5,3,3] ⁺	7200 (nc)
[5,3,3]	14400 (nc)

Veja também

Referências

HSM Coxeter, Regular Polytopes , 3rd Edition, Dover New York, 1973
Kaleidoscopes: Selected Writings of HSM Coxeter , editado por F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
- (Documento 22) HSM Coxeter, Regular and Semi Regular Polytopes I , [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Documento 23) HSM Coxeter, Regular and Semi-Regular Polytopes II , [Math. Zeit. 188 (1985) 559–591]
- (Documento 24) HSM Coxeter, Regular and Semi-Regular Polytopes III , [Math. Zeit. 200 (1988) 3-45]
HSM Coxeter e WOJ Moser. Geradores e relações para grupos discretos 4ª ed, Springer-Verlag. Nova york. 1980 p92, p122.
John .H. Conway e MJT Guy : Four-Dimensional Archimedean Polytopes , Proceedings of the Colloquium on Convexity at Copenhagen, page 38 und 39, 1965
NW Johnson : The Theory of Uniform Polytopes and Honeycombs , Ph.D. Dissertação, Universidade de Toronto, 1966
NW Johnson : Geometries and Transformations , (2018) ISBN 978-1-107-10340-5 Capítulo 11: Finite Symmetry Groups , 11.5 Spherical Coxeter groups , p. 249
John H. Conway e Derek A. Smith, On Quaternions and Octonions , 2003, ISBN 978-1-56881-134-5
John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Capítulo 26)

links externos

Weisstein, Eric W. "Uniform polychoron" . MathWorld .
Klitzing, Richard. "Polopos uniformes 4D" .

Languages

In other projects