Regressão de quantil - Quantile regression

Parte de uma série sobre
Análise de regressão
Modelos
Regressão linear Regressão simples Regressão polinomial Modelo linear geral
Modelo linear generalizado Escolha discreta Regressão binomial Regressão binária Regressão logística Regressão logística multinomial Logit misto Probit Probit multinomial Logit ordenado Probit ordenado Poisson
Modelo multinível Efeitos fixos Efeitos aleatórios Modelo linear de efeitos mistos Modelo de efeitos mistos não linear
Regressão não linear Não paramétrico Semiparamétrico Robusto Quantil Isotônico Componentes principais Ângulo mínimo Local Segmentado
Erros em variáveis
Estimativa
Mínimos quadrados Linear Não linear
Ordinário Pesada Generalizado
Parcial Total Não negativo Regressão de cume Regularizado
Desvios mínimos absolutos Reponderado iterativamente Bayesiano Multivariada bayesiana
Fundo
Validação de regressão Resposta média e prevista Erros e residuais Qualidade de ajuste Resíduo estudantizado Teorema de Gauss-Markov
Portal de matemática
v t e

A regressão quantílica é um tipo de análise de regressão usada em estatística e econometria. Enquanto o método dos mínimos quadrados estima a média condicional da variável de resposta entre os valores das variáveis ​​preditoras, a regressão de quantis estima a mediana condicional (ou outros quantis ) da variável de resposta. A regressão quantílica é uma extensão da regressão linear usada quando as condições da regressão linear não são atendidas.

Vantagens e aplicações

Uma vantagem da regressão de quantis em relação à regressão de mínimos quadrados ordinários é que as estimativas de regressão de quantis são mais robustas contra outliers nas medições de resposta. No entanto, a principal atração da regressão de quantis vai além disso e é vantajosa quando funções de quantis condicionais são de interesse. Diferentes medidas de tendência central e dispersão estatística podem ser úteis para obter uma análise mais abrangente da relação entre as variáveis.

Em ecologia , a regressão quantílica tem sido proposta e utilizada como forma de descobrir relações preditivas mais úteis entre variáveis ​​nos casos em que não há relação ou apenas uma relação fraca entre as médias dessas variáveis. A necessidade e o sucesso da regressão quantílica em ecologia tem sido atribuída à complexidade das interações entre diferentes fatores, levando a dados com variação desigual de uma variável para diferentes intervalos de outra variável.

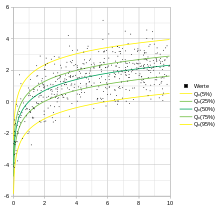
Outra aplicação da regressão de quantis é nas áreas de gráficos de crescimento, onde curvas de percentis são comumente usadas para rastrear crescimento anormal.

História

A ideia de estimar uma inclinação de regressão mediana, um teorema principal sobre a minimização da soma dos desvios absolutos e um algoritmo geométrico para construir a regressão mediana foi proposta em 1760 por Ruđer Josip Bošković , um padre católico jesuíta de Dubrovnik. Ele estava interessado na elipticidade da Terra, baseando-se na sugestão de Isaac Newton de que sua rotação poderia causar uma protuberância no equador com um achatamento correspondente nos pólos. Ele finalmente produziu o primeiro procedimento geométrico para determinar o equador de um planeta em rotação a partir de três observações de uma feição superficial. Mais importante para a regressão quantílica, ele foi capaz de desenvolver a primeira evidência do critério mínimo absoluto e precedeu os mínimos quadrados introduzidos por Legendre em 1805 em cinquenta anos.

Outros pensadores começaram a desenvolver a ideia de Bošković, como Pierre-Simon Laplace , que desenvolveu o chamado "método de situação". Isso levou à mediana plural de Francis Edgeworth - uma abordagem geométrica da regressão da mediana - e é reconhecida como o precursor do método simplex . As obras de Bošković, Laplace e Edgeworth foram reconhecidas como um prelúdio às contribuições de Roger Koenker para a regressão quantílica.

Os cálculos de regressão mediana para conjuntos de dados maiores são bastante tediosos em comparação com o método dos mínimos quadrados, razão pela qual historicamente gerou uma falta de popularidade entre os estatísticos, até a adoção generalizada de computadores na última parte do século XX.

Quantil

A regressão de quantil expressa os quantis condicionais de uma variável dependente como uma função linear das variáveis ​​explicativas. Crucial para a praticidade da regressão de quantis é que os quantis podem ser expressos como a solução de um problema de minimização, como mostraremos nesta seção antes de discutir os quantis condicionais na próxima seção.

Quantil de uma variável aleatória

Let Ser uma variável aleatória de valor real com função de distribuição cumulativa . O ésimo quantil de Y é dado por ${\ displaystyle Y}$ ${\ displaystyle F_ {Y} (y) = P (Y \ leq y)}$${\ displaystyle \ tau}$

${\ displaystyle q_ {Y} (\ tau) = F_ {Y} ^ {- 1} (\ tau) = \ inf \ left \ {y: F_ {Y} (y) \ geq \ tau \ right \}}$

Onde ${\ displaystyle \ tau \ in (0,1).}$

Defina a função de perda como , onde é uma função de indicador . ${\ displaystyle \ rho _ {\ tau} (y) = y (\ tau - \ mathbb {I} _ {(y <0)})}$${\ displaystyle \ mathbb {I}}$

Um quantil específico pode ser encontrado minimizando a perda esperada de em relação a : (pp. 5-6): ${\ displaystyle Yu}$${\ displaystyle u}$

${\ displaystyle q_ {Y} (\ tau) = {\ underset {u} {\ mbox {arg min}}} E (\ rho _ {\ tau} (Yu)) = {\ underset {u} {\ mbox {arg min}}} {\ biggl \ {} (\ tau -1) \ int _ {- \ infty} ^ {u} (yu) dF_ {Y} (y) + \ tau \ int _ {u} ^ {\ infty} (yu) dF_ {Y} (y) {\ biggr \}}.}$

Isso pode ser mostrado calculando a derivada da perda esperada por meio de uma aplicação da regra integral de Leibniz , definindo-a como 0, e deixando ser a solução de ${\ displaystyle q _ {\ tau}}$

${\ displaystyle 0 = (1- \ tau) \ int _ {- \ infty} ^ {q _ {\ tau}} dF_ {Y} (y) - \ tau \ int _ {q _ {\ tau}} ^ {\ infty} dF_ {Y} (y).}$

Esta equação se reduz a

${\ displaystyle 0 = F_ {Y} (q _ {\ tau}) - \ tau,}$

e então para

${\ displaystyle F_ {Y} (q _ {\ tau}) = \ tau.}$

Se a solução não é única, então temos de ter o menor como solução para obter o th quantil da variável aleatória Y . ${\ displaystyle q _ {\ tau}}$${\ displaystyle \ tau}$

Exemplo

Let Ser uma variável aleatória discreta que assume valores com probabilidades iguais. A tarefa é encontrar a mediana de Y e, portanto, o valor é escolhido. Então, a perda esperada de é ${\ displaystyle Y}$${\ displaystyle y_ {i} = i}$${\ displaystyle i = 1,2, \ dots, 9}$${\ displaystyle \ tau = 0,5}$${\ displaystyle Yu}$

${\ displaystyle L (u) = E (\ rho _ {\ tau} (Yu)) = {\ frac {(\ tau -1)} {9}} \ sum _ {y_ {i} <u}}$${\ displaystyle (y_ {i} -u)}$${\ displaystyle + {\ frac {\ tau} {9}} \ sum _ {y_ {i} \ geq u}}$${\ displaystyle (y_ {i} -u)}$${\ displaystyle = {\ frac {0,5} {9}} {\ Bigl (}}$${\ displaystyle -}$${\ displaystyle \ sum _ {y_ {i} <u}}$${\ displaystyle (y_ {i} -u)}$${\ displaystyle + \ sum _ {y_ {i} \ geq u}}$${\ displaystyle (y_ {i} -u)}$${\ displaystyle {\ Bigr)}.}$

Como é uma constante, ela pode ser retirada da função de perda esperada (isso só é verdadeiro se ). Então, em u = 3, ${\ displaystyle {0,5 / 9}}$${\ displaystyle \ tau = 0,5}$

${\ displaystyle L (3) \ propto \ sum _ {i = 1} ^ {2}}$${\ displaystyle - (i-3)}$${\ displaystyle + \ sum _ {i = 3} ^ {9}}$${\ displaystyle (i-3)}$${\ displaystyle = [(2 + 1) + (0 + 1 + 2 + ... + 6)] = 24.}$

Suponha que u seja aumentado em 1 unidade. Em seguida, a perda esperada será alterada ao mudar u para 4. Se, u = 5, a perda esperada é ${\ displaystyle (3) - (6) = - 3}$

${\ displaystyle L (5) \ propto \ sum _ {i = 1} ^ {4} i + \ sum _ {i = 0} ^ {4} i = 20,}$

e qualquer mudança em u aumentará a perda esperada. Portanto, u = 5 é a mediana. A Tabela abaixo mostra a perda esperada (dividida por ) para diferentes valores de u . ${\ displaystyle {0,5 / 9}}$

você	1	2	3	4	5	6	7	8	9
Perda esperada	36	29	24	21	20	21	24	29	36

Intuição

Considere e seja q uma estimativa inicial para . A perda esperada avaliada em q é ${\ displaystyle \ tau = 0,5}$${\ displaystyle q _ {\ tau}}$

${\ displaystyle L (q) = - 0,5 \ int _ {- \ infty} ^ {q} (yq) dF_ {Y} (y) +0,5 \ int _ {q} ^ {\ infty} (yq) dF_ { Y} (y).}$

Para minimizar a perda esperada, movemos o valor de q um pouco para ver se a perda esperada aumentará ou diminuirá. Suponha que aumentemos q em 1 unidade. Então, a mudança de perda esperada seria

${\ displaystyle \ int _ {- \ infty} ^ {q} 1dF_ {Y} (y) - \ int _ {q} ^ {\ infty} 1dF_ {Y} (y).}$

O primeiro termo da equação é e o segundo termo da equação é . Portanto, a mudança da função de perda esperada é negativa se e somente se , isto é, se e somente se q for menor que a mediana. Da mesma forma, se reduzirmos q em 1 unidade, a mudança da função de perda esperada é negativa se e somente se q for maior do que a mediana. ${\ displaystyle F_ {Y} (q)}$${\ displaystyle 1-F_ {Y} (q)}$${\ displaystyle F_ {Y} (q) <0,5}$

Para minimizar a função de perda esperada, aumentaríamos (diminuiríamos) L ( q ) se q fosse menor (maior) que a mediana, até q atingir a mediana. A ideia por trás da minimização é contar o número de pontos (ponderados com a densidade) que são maiores ou menores do que q e então mover q para um ponto onde q é maior do que % dos pontos. ${\ displaystyle 100 \ tau}$

Quantil de amostra

O quantil da amostra pode ser obtido resolvendo o seguinte problema de minimização ${\ displaystyle \ tau}$

${\ displaystyle {\ hat {q}} _ {\ tau} = {\ underset {q \ in \ mathbb {R}} {\ mbox {arg min}}} \ sum _ {i = 1} ^ {n} \ rho _ {\ tau} (y_ {i} -q),}$

${\ displaystyle = {\ underset {q \ in \ mathbb {R}} {\ mbox {arg min}}} \ left [(\ tau -1) \ sum _ {y_ {i} <q} (y_ {i } -q) + \ tau \ sum _ {y_ {i} \ geq q} (y_ {i} -q) \ right]}$,

onde a função é a função de valor absoluto inclinado. A intuição é a mesma do quantil da população. ${\ displaystyle \ rho _ {\ tau}}$

Quantil condicional e regressão de quantil

O º quantil condicional de dado é o º quantil da distribuição de probabilidade condicional de dado , ${\ displaystyle \ tau}$${\ displaystyle Y}$${\ displaystyle X}$${\ displaystyle \ tau}$${\ displaystyle Y}$${\ displaystyle X}$

${\ displaystyle Q_ {Y | X} (\ tau) = \ inf \ left \ {y: F_ {Y | X} (y) \ geq \ tau \ right \}}$.

Usamos uma maiúscula para denotar o quantil condicional para indicar que é uma variável aleatória. ${\ displaystyle Q}$

Na regressão de quantil para o ésimo quantil, assumimos que o ésimo quantil condicional é dado como uma função linear das variáveis ​​explicativas: ${\ displaystyle \ tau}$${\ displaystyle \ tau}$

${\ displaystyle Q_ {Y | X} (\ tau) = X \ beta _ {\ tau}}$.

Dada a função de distribuição de , pode ser obtido resolvendo ${\ displaystyle Y}$${\ displaystyle \ beta _ {\ tau}}$

${\ displaystyle \ beta _ {\ tau} = {\ underset {\ beta \ in \ mathbb {R} ^ {k}} {\ mbox {arg min}}} E (\ rho _ {\ tau} (YX \ beta)).}$

Resolver o análogo da amostra fornece o estimador de . ${\ displaystyle \ beta}$

${\ displaystyle {\ hat {\ beta _ {\ tau}}} = {\ underset {\ beta \ in \ mathbb {R} ^ {k}} {\ mbox {arg min}}} \ sum _ {i = 1} ^ {n} (\ rho _ {\ tau} (Y_ {i} -X_ {i} \ beta)).}$

Observe que quando a função de perda é proporcional à função de valor absoluto e, portanto, a regressão mediana é o mesmo que a regressão linear por menores desvios absolutos . ${\ displaystyle \ tau = 0,5}$${\ displaystyle \ rho _ {\ tau}}$

Cálculo de estimativas para parâmetros de regressão

As formas matemáticas que surgem da regressão de quantis são distintas daquelas que surgem no método dos mínimos quadrados . O método dos mínimos quadrados leva a uma consideração de problemas em um espaço de produto interno , envolvendo projeção em subespaços e, portanto, o problema de minimizar os erros de quadrados pode ser reduzido a um problema de álgebra linear numérica . A regressão quantílica não possui esta estrutura e, em vez disso, o problema de minimização pode ser reformulado como um problema de programação linear .

${\ displaystyle {\ underset {\ beta, u ^ {+}, u ^ {-} \ in \ mathbb {R} ^ {k} \ times \ mathbb {R} _ {+} ^ {2n}} {\ min}} \ left \ {\ tau 1_ {n} ^ {'} u ^ {+} + (1- \ tau) 1_ {n} ^ {'} u ^ {-} | X \ beta + u ^ { +} - u ^ {-} = Y \ right \},}$

Onde

${\ displaystyle u_ {j} ^ {+} = \ max (u_ {j}, 0)}$ ,    ${\ displaystyle u_ {j} ^ {-} = - \ min (u_ {j}, 0).}$

Métodos simplex ou métodos de pontos internos podem ser aplicados para resolver o problema de programação linear.

Propriedades assintóticas

Pois , sob algumas condições de regularidade, é assintoticamente normal : ${\ displaystyle \ tau \ in (0,1)}$${\ displaystyle {\ hat {\ beta}} _ {\ tau}}$

${\ displaystyle {\ sqrt {n}} ({\ hat {\ beta}} _ {\ tau} - \ beta _ {\ tau}) {\ overset {d} {\ rightarrow}} N (0, \ tau (1- \ tau) D ^ {- 1} \ Omega _ {x} D ^ {- 1}),}$

Onde

${\ displaystyle D = E (f_ {Y} (X \ beta) XX ^ {\ prime})}$ e ${\ displaystyle \ Omega _ {x} = E (X ^ {\ prime} X).}$

A estimativa direta da matriz de variância-covariância assintótica nem sempre é satisfatória. A inferência para parâmetros de regressão de quantis pode ser feita com os testes de classificação de classificação de regressão ou com os métodos de bootstrap.

Equivariância

Veja estimador de invariante para histórico de invariância ou veja equivariância .

Equivariância de escala

Para qualquer e${\ displaystyle a> 0}$${\ displaystyle \ tau \ in [0,1]}$

${\ displaystyle {\ hat {\ beta}} (\ tau; aY, X) = a {\ hat {\ beta}} (\ tau; Y, X),}$

${\ displaystyle {\ hat {\ beta}} (\ tau; -aY, X) = - a {\ hat {\ beta}} (1- \ tau; Y, X).}$

Shift equivariância

Para qualquer e${\ displaystyle \ gamma \ in R ^ {k}}$${\ displaystyle \ tau \ in [0,1]}$

${\ displaystyle {\ hat {\ beta}} (\ tau; Y + X \ gamma, X) = {\ hat {\ beta}} (\ tau; Y, X) + \ gamma.}$

Equivariância para reparametrização de design

Seja qualquer matriz não singular e${\ displaystyle A}$${\ displaystyle p \ times p}$${\ displaystyle \ tau \ in [0,1]}$

${\ displaystyle {\ hat {\ beta}} (\ tau; Y, XA) = A ^ {- 1} {\ hat {\ beta}} (\ tau; Y, X).}$

Invariância para transformações monótonas

Se for uma função não decrescente ativada , a seguinte propriedade de invariância se aplica: ${\ displaystyle h}$${\ displaystyle \ mathbb {R}}$

${\ displaystyle h (Q_ {Y | X} (\ tau)) \ equiv Q_ {h (Y) | X} (\ tau).}$

Exemplo 1):

Se e , então . A regressão média não tem a mesma propriedade, pois${\ displaystyle W = \ exp (Y)}$${\ displaystyle Q_ {Y | X} (\ tau) = X \ beta _ {\ tau}}$${\ displaystyle Q_ {W | X} (\ tau) = \ exp (X \ beta _ {\ tau})}$${\ displaystyle \ operatorname {E} (\ ln (Y)) \ neq \ ln (\ operatorname {E} (Y)).}$

Métodos bayesianos para regressão de quantis

Como a regressão quantílica normalmente não assume uma probabilidade paramétrica para as distribuições condicionais de Y | X, os métodos bayesianos funcionam com uma probabilidade de trabalho. Uma escolha conveniente é a probabilidade laplaciana assimétrica, porque o modo do posterior resultante sob um prior plano são as estimativas de regressão de quantis usuais. A inferência posterior, entretanto, deve ser interpretada com cuidado. Yang, Wang e He forneceram um ajuste de variância posterior para inferência válida. Além disso, Yang e He mostraram que é possível ter inferência posterior assintoticamente válida se a probabilidade de trabalho for escolhida para ser a probabilidade empírica.

Métodos de aprendizado de máquina para regressão de quantis

Além da regressão linear simples, existem vários métodos de aprendizado de máquina que podem ser estendidos para a regressão quantílica. Uma mudança do erro quadrático para a função de perda de valor absoluto inclinado permite que algoritmos de aprendizagem baseados em descida de gradiente aprendam um quantil especificado em vez da média. Isso significa que podemos aplicar todas as redes neurais e algoritmos de aprendizado profundo à regressão quantílica. Algoritmos de aprendizagem baseados em árvore também estão disponíveis para regressão de quantis (veja, por exemplo, Florestas de Regressão de Quantis, como uma generalização simples de Florestas Aleatórias ).

Regressão de quantis censurados

Se a variável de resposta está sujeita a censura, a média condicional não é identificável sem suposições distribucionais adicionais, mas o quantil condicional é freqüentemente identificável. Para trabalhos recentes sobre regressão de quantis censurados, consulte: Portnoy e Wang e Wang

Exemplo (2):

Deixe e . Então . Este é o modelo de regressão de quantis censurados: os valores estimados podem ser obtidos sem fazer nenhuma suposição de distribuição, mas ao custo de dificuldade computacional, algumas das quais podem ser evitadas usando um procedimento de regressão de quantis censurado de três etapas simples como uma aproximação. ${\ displaystyle Y ^ {c} = \ max (0, Y)}$${\ displaystyle Q_ {Y | X} = X \ beta _ {\ tau}}$${\ displaystyle Q_ {Y ^ {c} | X} (\ tau) = \ max (0, X \ beta _ {\ tau})}$

Para censura aleatória nas variáveis ​​de resposta, a regressão de quantis censurados de Portnoy (2003) fornece estimativas consistentes de todas as funções de quantis identificáveis ​​com base na reponderação de cada ponto censurado de forma adequada.

Implementações

Numerosos pacotes de software estatístico incluem implementações de regressão de quantis:

• Função Matlabquantreg
• Eviews , desde a versão 6.
• gretl tem o quantregcomando.
• R oferece vários pacotes que implementam regressão quantílica, mais notavelmente quantregpor Roger Koenker , mas também gbm, quantregForest, qrnneqgam
• Python , via Scikit-gardenestatsmodels
• SAS a proc quantreg(versão 9.2) e proc quantselect(versão 9.3).
• Stata , por meio do qregcomando.
• Vowpal Wabbit , via --loss_function quantile.
• Pacote MathematicaQuantileRegression.m hospedado no projeto MathematicaForPrediction no GitHub.

Referências

Leitura adicional

• Angrist, Joshua D .; Pischke, Jörn-Steffen (2009). "Quantile Regression" . Mostly Harmless Econometrics: An Empiricist's Companion . Princeton University Press. pp. 269–291. ISBN 978-0-691-12034-8.
• Koenker, Roger (2005). Regressão de quantis . Cambridge University Press. ISBN 978-0-521-60827-5.