Gás Fermi - Fermi gas

Física de matéria condensada
Fases  · Transição de fase  · QCP
Estados da matéria Sólido  · líquido  · Gás  · Plasma  · Bose-Einstein  · gás Bose  · fermiônicos condensado  · gás de Fermi  · Fermi líquido  · supersólidos  · Superfluidez  · Luttinger líquido  · cristal Tempo
Fenômenos de fase Parâmetro de pedido  · Transição de fase  · QCP
Fases eletronicas Teoria de bandas  · Plasma  · Insulator  · Mott isolante  · Semiconductor  · semimetal  · condutor  · Superconductor  · Termelétrica  · piezoelétrico  · ferroelétricos  · isolante topológico  · semicondutores rotação gapless
Fenômenos eletrônicos Efeito Quantum Hall  · Efeito Spin Hall  · Efeito Kondo
Fases magnéticas Diamagnet  · Superdiamagnet paramagnet  · Superparamagnet ferromagneto  · antiferromagneto Metamagnet  · vidro de spin
Quasipartículas Phonon  · Exciton  · Plasmon Polariton  · Polaron  · Magnon
Matéria mole Sólido amorfo  · Colóide  · Material granular  · Cristal líquido  · Polímero
Cientistas Van der Waals  · Onnes  · von Laue  · Bragg  · Debye  · Bloch  · Onsager  · Mott  · Peierls  · Landau  · Luttinger  · Anderson  · Van Vleck  · Hubbard  · Shockley  · Bardeen  · Cooper  · Schrieffer  · Josephson  · Louis Néel  · Esaki  · Giaever  · Kohn  · Kadanoff  · Fisher  · Wilson  · von Klitzing  · Binnig  · Rohrer  · Bednorz  · Müller  · Laughlin  · Störmer  · Yang  · Tsui  · Abrikosov  · Ginzburg  · Leggett
Portal de física  Categoria
v t e

Um gás Fermi ideal é um estado da matéria que é um conjunto de muitos férmions não interagentes . Os férmions são partículas que obedecem às estatísticas de Fermi-Dirac , como elétrons , prótons e nêutrons e, em geral, partículas com spin meio inteiro . Essas estatísticas determinam a distribuição de energia dos férmions em um gás Fermi em equilíbrio térmico e são caracterizadas por sua densidade numérica , temperatura e o conjunto de estados de energia disponíveis. O modelo tem o nome do físico italiano Enrico Fermi .

Este modelo físico pode ser aplicado com precisão a muitos sistemas com muitos férmions. Alguns exemplos importantes são o comportamento de portadores de carga em um metal , núcleos em um núcleo atômico , nêutrons em uma estrela de nêutrons e elétrons em uma anã branca .

Descrição

Ilustração dos estados de energia: Diagrama de ocupação de energia para um sistema com 7 níveis de energia, a energia é degenerada vezes (há estados que têm uma energia de ) e tem uma ocupação dada por , com . Pelo princípio de exclusão de Pauli , até férmions podem ocupar um nível de energia do sistema, onde está o Spin dos férmions.${\ displaystyle E_ {i}}$${\ displaystyle D_ {i}}$${\ displaystyle D_ {i}}$${\ displaystyle E_ {i}}$${\ displaystyle N_ {i}}$${\ displaystyle i = 1,2,3,4,5,6,7}$${\ displaystyle (2j + 1) \ cdot D_ {i}}$${\ displaystyle E_ {i}}$${\ displaystyle j}$

Um gás Fermi ideal ou gás Fermi livre é um modelo físico que assume uma coleção de férmions não interagentes em um poço de potencial constante . Os férmions são partículas elementares ou compostas com spin meio-inteiro , portanto, seguem as estatísticas de Fermi-Dirac . O modelo equivalente para partículas inteiras de spin é chamado de gás de Bose (um conjunto de bósons não interagentes ). Com densidade de partículas suficientemente baixa e alta temperatura, tanto o gás Fermi quanto o gás de Bose se comportam como um gás ideal clássico .

Pelo princípio de exclusão de Pauli , nenhum estado quântico pode ser ocupado por mais de um férmion com um conjunto idêntico de números quânticos . Assim, um gás Fermi sem interação, ao contrário do gás de Bose, concentra um pequeno número de partículas por energia. Assim, um gás Fermi está proibido de condensar em um condensado de Bose-Einstein , embora os gases de Fermi de interação fraca possam formar um par de Cooper e condensado (também conhecido como regime de cruzamento BCS- BEC). A energia total do gás Fermi no zero absoluto é maior do que a soma dos estados fundamentais de uma única partícula porque o princípio de Pauli implica um tipo de interação ou pressão que mantém os férmions separados e em movimento. Por esta razão, a pressão de um gás Fermi é diferente de zero mesmo na temperatura zero, em contraste com a de um gás ideal clássico. Por exemplo, essa chamada pressão de degenerescência estabiliza uma estrela de nêutrons (um gás Fermi de nêutrons) ou uma estrela anã branca (um gás Fermi de elétrons) contra a atração da gravidade para dentro , que aparentemente colapsaria a estrela em um buraco negro . Somente quando uma estrela tem massa suficiente para superar a pressão da degeneração, ela pode colapsar em uma singularidade.

É possível definir uma temperatura de Fermi abaixo da qual o gás pode ser considerado degenerado (sua pressão deriva quase exclusivamente do princípio de Pauli). Essa temperatura depende da massa dos férmions e da densidade dos estados de energia .

A suposição principal do modelo de elétron livre para descrever os elétrons deslocalizados em um metal pode ser derivada do gás de Fermi. Uma vez que as interações são negligenciadas devido ao efeito de triagem , o problema de tratar as propriedades de equilíbrio e a dinâmica de um gás de Fermi ideal reduz-se ao estudo do comportamento de partículas individuais independentes. Nesses sistemas, a temperatura de Fermi é geralmente de muitos milhares de kelvins , portanto, em aplicações humanas, o gás de elétron pode ser considerado degenerado. A energia máxima dos férmions na temperatura zero é chamada de energia de Fermi . A superfície de energia de Fermi no espaço recíproco é conhecida como superfície de Fermi .

O modelo de elétron quase livre adapta o modelo de gás Fermi para considerar a estrutura cristalina de metais e semicondutores , onde elétrons em uma rede cristalina são substituídos por elétrons de Bloch com um momento cristalino correspondente . Como tal, os sistemas periódicos ainda são relativamente tratáveis ​​e o modelo forma o ponto de partida para teorias mais avançadas que lidam com interações, por exemplo, usando a teoria de perturbação .

Gás uniforme 1D

O poço quadrado infinito unidimensional de comprimento L é um modelo para uma caixa unidimensional com a energia potencial:

${\ displaystyle V (x) = {\ begin {cases} 0, & x_ {c} - {\ tfrac {L} {2}} <x <x_ {c} + {\ tfrac {L} {2}}, \\\ infty, & {\ text {caso contrário.}} \ end {cases}}}$

É um sistema-modelo padrão em mecânica quântica para o qual a solução para uma única partícula é bem conhecida. Como o potencial dentro da caixa é uniforme, este modelo é referido como gás uniforme 1D, embora o perfil de densidade numérica real do gás possa ter nós e anti-nós quando o número total de partículas é pequeno.

Os níveis são rotulados por um único número quântico n e as energias são dadas por:

${\ displaystyle E_ {n} = E_ {0} + {\ frac {\ hbar ^ {2} \ pi ^ {2}} {2mL ^ {2}}} n ^ {2}. \,}$

onde é a energia do ponto zero (que pode ser escolhida arbitrariamente como uma forma de fixação do medidor ), a massa de um único férmion e é a constante de Planck reduzida . ${\ displaystyle E_ {0}}$${\ displaystyle m}$${\ displaystyle \ hbar}$

Para N férmions com spin ½ na caixa, não mais do que duas partículas podem ter a mesma energia, ou seja, duas partículas podem ter a energia de , duas outras partículas podem ter energia e assim por diante. As duas partículas de mesma energia têm spin ½ (spin para cima) ou −½ (spin para baixo), levando a dois estados para cada nível de energia. Na configuração para a qual a energia total é mais baixa (o estado fundamental), todos os níveis de energia até n  =  N / 2 são ocupados e todos os níveis superiores estão vazios. ${\ textstyle E_ {1}}$${\ textstyle E_ {2}}$

Definindo a referência para a energia de Fermi ser , a energia de Fermi é, portanto, dada por ${\ displaystyle E_ {0}}$

${\ displaystyle E _ {\ mathrm {F}} ^ {({\ text {1D}})} = E_ {n} -E_ {0} = {\ frac {\ hbar ^ {2} \ pi ^ {2} } {2mL ^ {2}}} \ left (\ left \ lfloor {\ frac {N} {2}} \ right \ rfloor \ right) ^ {2},}$

onde é a função de piso avaliada em n  =  N / 2. ${\ displaystyle \ left \ lfloor {\ frac {N} {2}} \ right \ rfloor}$

Limite termodinâmico

No limite termodinâmico , o número total de partículas N é tão grande que o número quântico n pode ser tratado como uma variável contínua. Nesse caso, o perfil geral de densidade numérica na caixa é de fato uniforme.

O número de estados quânticos no intervalo é: ${\ displaystyle n_ {1} <n <n_ {1} + \ operatorname {d} \! n}$

${\ displaystyle D_ {n} (n_ {1}) \ operatorname {d} \! n = 2 \ operatorname {d} \! n \ ,.}$

Sem perda de generalidade , a energia do ponto zero é escolhida para ser zero, com o seguinte resultado:

${\ displaystyle E_ {n} = {\ frac {\ hbar ^ {2} \ pi ^ {2}} {2mL ^ {2}}} n ^ {2} \ implica \ operatorname {d} \! E = { \ frac {\ hbar ^ {2} \ pi ^ {2}} {mL ^ {2}}} n \ operatorname {d} \! n = {\ frac {\ hbar \ pi} {L}} {\ sqrt {\ frac {2E} {m}}} \ operatorname {d} \! n \ ,.}$

Portanto, no intervalo:

${\ displaystyle E_ {1} = {\ frac {\ hbar ^ {2} \ pi ^ {2}} {2mL ^ {2}}} n_ {1} ^ {2} <E <E_ {1} + \ operatorname {d} \! E \ ,,}$

o número de estados quânticos é:

${\ displaystyle D_ {n} (n_ {1}) \ operatorname {d} \! n = 2 {\ frac {\ operatorname {d} \! E} {\ operatorname {d} \! E / \ operatorname {d} \! E} {\ operatorname {d} \! E / \ operatorname {d } \! n}} = {\ frac {2} {{\ frac {\ hbar ^ {2} \ pi ^ {2}} {mL ^ {2}}} n}} \ operatorname {d} \! E \ equiv D (E_ {1}) \ operatorname {d} \! E \ ,.}$

Aqui, o grau de degeneração é:

${\ displaystyle D (E) = {\ frac {2} {\ operatorname {d} \! E / \ operatorname {d} \! n}} = {\ frac {2L} {\ hbar \ pi}} {\ sqrt {\ frac {m} {2E}}} \,}$

E a densidade de estados é:

${\ displaystyle g (E) \ equiv {\ frac {1} {L}} D (E) = {\ frac {2} {\ hbar \ pi}} {\ sqrt {\ frac {m} {2E}} } \ ,.}$

Na literatura moderna, o que está acima é algumas vezes chamado de "densidade de estados". No entanto, difere por um fator do volume do sistema (que é neste caso 1D). ${\ displaystyle D (E)}$${\ displaystyle g (E)}$${\ displaystyle D (E)}$${\ displaystyle L}$

Com base na seguinte fórmula:

${\ displaystyle \ int _ {0} ^ {E_ {F}} D (E) dE = N \ ,,}$

a energia de Fermi no limite termodinâmico pode ser calculada como:

${\ displaystyle E _ {\ mathrm {F}} ^ {({\ text {1D}})} = {\ frac {\ hbar ^ {2} \ pi ^ {2}} {2mL ^ {2}}} \ esquerda ({\ frac {N} {2}} \ direita) ^ {2} \ ,.}$

Gás uniforme 3D

Um modelo do núcleo atômico mostrando-o como um feixe compacto de dois tipos de núcleons : prótons (vermelho) e nêutrons (azul). Como uma primeira aproximação, o núcleo pode ser tratado como composto de gases de prótons e nêutrons não interagentes.

O caso do gás de Fermi uniforme isotrópico tridimensional e não relativístico é conhecido como esfera de Fermi .

Um poço quadrado infinito tridimensional (ou seja, uma caixa cúbica que tem um comprimento lateral L ) tem a energia potencial

${\ displaystyle V (x, y, z) = {\ begin {cases} 0, & - {\ frac {L} {2}} <x, y, z <{\ frac {L} {2}}, \\\ infty, & {\ text {caso contrário.}} \ end {cases}}}$

Os estados agora são rotulados por três números quânticos n _x , n _y e n _z . As energias de uma única partícula são

${\ displaystyle E_ {n_ {x}, n_ {y}, n_ {z}} = E_ {0} + {\ frac {\ hbar ^ {2} \ pi ^ {2}} {2mL ^ {2}} } \ left (n_ {x} ^ {2} + n_ {y} ^ {2} + n_ {z} ^ {2} \ right) \,}$,

onde n _x , n _y , n _z são inteiros positivos. Nesse caso, vários estados têm a mesma energia (conhecidos como níveis de energia degenerados ), por exemplo . ${\ displaystyle E_ {211} = E_ {121} = E_ {112}}$

Limite termodinâmico

Quando a caixa contém N férmions não interagentes de spin ½, é interessante calcular a energia no limite termodinâmico, onde N é tão grande que os números quânticos n _x , n _y , n _z podem ser tratados como variáveis ​​contínuas.

Com o vetor , cada estado quântico corresponde a um ponto no 'n-espaço' com energia ${\ displaystyle \ mathbf {n} = (n_ {x}, n_ {y}, n_ {z})}$

${\ displaystyle E _ {\ mathbf {n}} = E_ {0} + {\ frac {\ hbar ^ {2} \ pi ^ {2}} {2mL ^ {2}}} | \ mathbf {n} | ^ {2} \,}$

Com denotando o quadrado do comprimento euclidiano usual . O número de estados com energia menor que E _F  +   E ₀ é igual ao número de estados que estão dentro de uma esfera de raio na região do n-espaço onde n _x , n _y , n _z são positivos. No estado fundamental, este número é igual ao número de férmions no sistema: ${\ displaystyle | \ mathbf {n} | ^ {2}}$${\ displaystyle | \ mathbf {n} | = {\ sqrt {n_ {x} ^ {2} + n_ {y} ^ {2} + n_ {z} ^ {2}}}}$${\ displaystyle | \ mathbf {n} _ {\ mathrm {F}} |}$

${\ displaystyle N = 2 \ times {\ frac {1} {8}} \ times {\ frac {4} {3}} \ pi n _ {\ mathrm {F}} ^ {3} \,}$

Os férmions livres que ocupam os estados de energia mais baixos formam uma esfera no espaço recíproco . A superfície desta esfera é a superfície de Fermi .

O fator de dois expressa os dois estados de spin, e o fator de 1/8 expressa a fração da esfera que se encontra na região onde todos os n são positivos.

${\ displaystyle n _ {\ mathrm {F}} = \ left ({\ frac {3N} {\ pi}} \ right) ^ {1/3}}$

A energia Fermi é dada por

${\ displaystyle E _ {\ mathrm {F}} = {\ frac {\ hbar ^ {2} \ pi ^ {2}} {2mL ^ {2}}} n _ {\ mathrm {F}} ^ {2} = {\ frac {\ hbar ^ {2} \ pi ^ {2}} {2mL ^ {2}}} \ left ({\ frac {3N} {\ pi}} \ right) ^ {2/3}}$

O que resulta em uma relação entre a energia de Fermi e o número de partículas por volume (quando L ² é substituído por V ^2/3 ):

${\ displaystyle E _ {\ mathrm {F}} = {\ frac {\ hbar ^ {2}} {2m}} \ left ({\ frac {3 \ pi ^ {2} N} {V}} \ right) ^ {2/3} \,}$

Esta também é a energia da partícula de energia mais alta (a partícula ésima), acima da energia do ponto zero . A ª partícula tem uma energia de ${\ displaystyle N}$${\ displaystyle E_ {0}}$${\ displaystyle N '}$

${\ displaystyle E_ {N '} = E_ {0} + {\ frac {\ hbar ^ {2}} {2m}} \ left ({\ frac {3 \ pi ^ {2} N'} {V}} \ direita) ^ {2/3} \, = E_ {0} + E _ {\ mathrm {F}} {\ big |} _ {N '}}$

A energia total de uma esfera de férmions de Fermi (que ocupa todos os estados de energia dentro da esfera de Fermi) é dada por: ${\ displaystyle N}$${\ displaystyle N}$

${\ displaystyle E _ {\ rm {T}} = NE_ {0} + \ int _ {0} ^ {N} E _ {\ mathrm {F}} {\ big |} _ {N ^ {\ prime}} \ , \ mathrm {d} N ^ {\ prime} = \ left ({\ frac {3} {5}} E _ {\ mathrm {F}} + E_ {0} \ right) N}$

Portanto, a energia média por partícula é dada por:

${\ displaystyle E _ {\ mathrm {av}} = E_ {0} + {\ frac {3} {5}} E _ {\ mathrm {F}}}$

Densidade de estados

Densidade de estados (DOS) de um gás Fermi em 3 dimensões

Para o gás Fermi uniforme 3D, com férmions de spin-½, o número de partículas em função da energia é obtido substituindo a energia de Fermi por uma energia variável : ${\ textstyle N (E)}$${\ textstyle (E-E_ {0})}$

${\ displaystyle N (E) = {\ frac {V} {3 \ pi ^ {2}}} \ left [{\ frac {2m} {\ hbar ^ {2}}} (E-E_ {0}) \ direita] ^ {3/2}}$,

a partir da qual a densidade de estados (número de estados de energia por energia por volume) pode ser obtida. Pode ser calculado diferenciando o número de partículas em relação à energia: ${\ displaystyle g (E)}$

${\ displaystyle g (E) = {\ frac {1} {V}} {\ frac {\ parcial N (E)} {\ parcial E}} = {\ frac {1} {2 \ pi ^ {2} }} \ left ({\ frac {2m} {\ hbar ^ {2}}} \ right) ^ {3/2} {\ sqrt {E-E_ {0}}}}$.

Este resultado fornece uma maneira alternativa de calcular a energia total de uma esfera de férmions de Fermi (que ocupa todos os estados de energia dentro da esfera de Fermi): ${\ displaystyle N}$${\ displaystyle N}$

${\ displaystyle {\ begin {alinhados} E_ {T} & = \ int _ {0} ^ {N} E \ mathrm {d} N (E) = EN (E) {\ big |} _ {0} ^ {N} - \ int _ {E_ {0}} ^ {E_ {0} + E_ {F}} N (E) \ mathrm {d} E \\ & = (E_ {0} + E_ {F}) N- \ int _ {0} ^ {E_ {F}} N (E) \ mathrm {d} (E-E_ {0}) \\ & = (E_ {0} + E_ {F}) N- { \ frac {2} {5}} E_ {F} N (E_ {F}) = \ left (E_ {0} + {\ frac {3} {5}} E _ {\ mathrm {F}} \ right) N \ end {alinhado}}}$

Quantidades termodinâmicas

Pressão de degenerescência

Curvas de pressão x temperatura de gases clássicos e quânticos ideais (gás Fermi, gás de Bose ) em três dimensões. A repulsão de Pauli em férmions (como elétrons) dá a eles uma pressão adicional sobre um gás clássico equivalente, mais significativamente em baixa temperatura.

Usando a primeira lei da termodinâmica , esta energia interna pode ser expressa como uma pressão, ou seja,

${\ displaystyle P = - {\ frac {\ partial E _ {\ rm {T}}} {\ partial V}} = {\ frac {2} {5}} {\ frac {N} {V}} E_ { \ mathrm {F}} = {\ frac {(3 \ pi ^ {2}) ^ {2/3} \ hbar ^ {2}} {5m}} \ left ({\ frac {N} {V}} \ direita) ^ {5/3},}$

onde esta expressão permanece válida para temperaturas muito menores que a temperatura de Fermi. Essa pressão é conhecida como pressão de degenerescência . Nesse sentido, os sistemas compostos por férmions também são chamados de matéria degenerada .

Estrelas padrão evitam o colapso equilibrando a pressão térmica ( plasma e radiação) contra as forças gravitacionais. No final da vida da estrela, quando os processos térmicos são mais fracos, algumas estrelas podem se tornar anãs brancas, que só são sustentadas contra a gravidade pela pressão de degeneração de elétrons . Usando o gás Fermi como modelo, é possível calcular o limite de Chandrasekhar , ou seja, a massa máxima que qualquer estrela pode adquirir (sem pressão gerada termicamente significativa) antes de colapsar em um buraco negro ou estrela de nêutrons. Esta última, é uma estrela composta principalmente de nêutrons, onde o colapso também é evitado pela pressão de degeneração de nêutrons.

Para o caso de metais, a pressão de degenerescência de elétrons contribui para a compressibilidade ou módulo de volume do material.

Potencial químico

Assumindo que a concentração de férmions não muda com a temperatura, então o potencial químico total µ (nível de Fermi) do gás de Fermi ideal tridimensional está relacionado à energia de Fermi de temperatura zero E _F por uma expansão de Sommerfeld (assumindo ): ${\ displaystyle k _ {\ rm {B}} T \ ll E _ {\ mathrm {F}}}$

${\ displaystyle \ mu (T) = E_ {0} + E _ {\ mathrm {F}} \ left [1 - {\ frac {\ pi ^ {2}} {12}} \ left ({\ frac {k_ {\ rm {B}} T} {E _ {\ mathrm {F}}}} \ right) ^ {2} - {\ frac {\ pi ^ {4}} {80}} \ left ({\ frac { k _ {\ rm {B}} T} {E _ {\ mathrm {F}}}} \ right) ^ {4} + \ cdots \ right]}$,

onde T é a temperatura .

Por isso, o potencial químico interno , μ - E ₀ , é aproximadamente igual à energia de Fermi em temperaturas que são muito mais baixas do que a temperatura de Fermi característica T _F . Esta temperatura característica é da ordem de 10 ⁵ K para um metal, portanto, à temperatura ambiente (300 K), a energia de Fermi e o potencial químico interno são essencialmente equivalentes.

Valores tipicos

Metais

No modelo do elétron livre , os elétrons em um metal podem ser considerados como formando um gás de Fermi uniforme. A densidade numérica de elétrons de condução em metais varia entre aproximadamente 10 ²⁸ e 10 ²⁹ elétrons por m ³ , que também é a densidade típica de átomos na matéria sólida comum. Esta densidade numérica produz uma energia Fermi da ordem: ${\ displaystyle N / V}$

${\ displaystyle E _ {\ mathrm {F}} = {\ frac {\ hbar ^ {2}} {2m_ {e}}} \ left (3 \ pi ^ {2} \ 10 ^ {28 \ \ sim \ 29 } \ \ mathrm {m} ^ {- 3} \ right) ^ {2/3} \ approx 2 \ \ sim \ 10 \ \ mathrm {eV}}$,

onde m _e é a massa de repouso do elétron . Essa energia de Fermi corresponde a uma temperatura de Fermi da ordem de 10 ⁶ kelvins, muito mais alta do que a temperatura da superfície do sol . Qualquer metal irá ferver antes de atingir essa temperatura sob pressão atmosférica. Assim, para qualquer finalidade prática, um metal pode ser considerado um gás Fermi à temperatura zero como uma primeira aproximação (as temperaturas normais são pequenas em comparação com T _F ).

Anãs brancas

Estrelas conhecidas como anãs brancas têm massa comparável ao nosso Sol , mas têm cerca de um centésimo de seu raio. As altas densidades significam que os elétrons não estão mais ligados a um único núcleo e, em vez disso, formam um gás de elétron degenerado. A densidade numérica de elétrons em uma anã branca é da ordem de 10 ³⁶ elétrons / m ³ . Isso significa que sua energia Fermi é:

${\ displaystyle E _ {\ mathrm {F}} = {\ frac {\ hbar ^ {2}} {2m_ {e}}} \ left ({\ frac {3 \ pi ^ {2} (10 ^ {36} )} {1 \ \ mathrm {m} ^ {3}}} \ right) ^ {2/3} \ aproximadamente 3 \ vezes 10 ^ {5} \ \ mathrm {eV} = 0,3 \ \ mathrm {MeV}}$

Núcleo

Outro exemplo típico é o das partículas no núcleo de um átomo. O raio do núcleo é aproximadamente:

${\ displaystyle R = \ left (1,25 \ times 10 ^ {- 15} \ mathrm {m} \ right) \ vezes A ^ {1/3}}$

onde A é o número de núcleons .

A densidade numérica de núcleos em um núcleo é, portanto:

${\ displaystyle \ rho = {\ frac {A} {{\ begin {matrix} {\ frac {4} {3}} \ end {matrix}} \ pi R ^ {3}}} \ approx 1,2 \ times 10 ^ {44} \ \ mathrm {m} ^ {- 3}}$

Essa densidade deve ser dividida por dois, porque a energia de Fermi só se aplica a férmions do mesmo tipo. A presença de nêutrons não afeta a energia de Fermi dos prótons no núcleo e vice-versa.

A energia Fermi de um núcleo é aproximadamente:

${\ displaystyle E _ {\ mathrm {F}} = {\ frac {\ hbar ^ {2}} {2m _ {\ rm {p}}}} \ left ({\ frac {3 \ pi ^ {2} (6 \ vezes 10 ^ {43})} {1 \ \ mathrm {m} ^ {3}}} \ direita) ^ {2/3} \ aproximadamente 3 \ vezes 10 ^ {7} \ \ mathrm {eV} = 30 \ \ mathrm {MeV}}$,

onde m _p é a massa do próton.

O raio do núcleo admite desvios em torno do valor mencionado acima, portanto, um valor típico para a energia de Fermi é normalmente dado como 38 MeV .

Gás uniforme com dimensão arbitrária

Densidade de estados

Usando um volume integral nas dimensões, a densidade dos estados é: ${\ textstyle d}$

${\ displaystyle g ^ {(d)} (E) = g_ {s} \ int {\ frac {\ mathrm {d} ^ {d} \ mathbf {k}} {(2 \ pi) ^ {d}} } \ delta \ left (E-E_ {0} - {\ frac {\ hbar ^ {2} | \ mathbf {k} | ^ {2}} {2m}} \ right) = g_ {s} \ \ left ({\ frac {m} {2 \ pi \ hbar ^ {2}}} \ direita) ^ {d / 2} {\ frac {(E-E_ {0}) ^ {d / 2-1}} { \ Gamma (d / 2)}}}$

A energia de Fermi é obtida procurando a densidade numérica das partículas:

${\ displaystyle \ rho = {\ frac {N} {V}} = \ int _ {E_ {0}} ^ {E_ {0} + E _ {\ mathrm {F}} ^ {(d)}} g ^ {(d)} (E) \, \ mathrm {d} E}$

Para obter:

${\ displaystyle E _ {\ mathrm {F}} ^ {(d)} = {\ frac {2 \ pi \ hbar ^ {2}} {m}} \ left ({\ tfrac {1} {g_ {s} }} \ Gamma \ left ({\ tfrac {d} {2}} + 1 \ right) {\ frac {N} {V}} \ right) ^ {2 / d}}$

onde está o volume d- dimensional correspondente, é a dimensão para o espaço de Hilbert interno. Para o caso de spin-½, toda energia é duas vezes degenerada, então neste caso . ${\ textstyle V}$${\ textstyle g_ {s}}$${\ textstyle g_ {s} = 2}$

Um resultado particular é obtido para , onde a densidade de estados torna-se uma constante (não depende da energia): ${\ displaystyle d = 2}$

${\ displaystyle g ^ {(2 \ mathrm {D})} (E) = {\ frac {g_ {s}} {2}} {\ frac {m} {\ pi \ hbar ^ {2}}}}$.

Gás Fermi em armadilha harmônica

O potencial de armadilha harmônica :

${\ displaystyle V (x, y, z) = {\ frac {1} {2}} m \ omega _ {x} ^ {2} x ^ {2} + {\ frac {1} {2}} m \ omega _ {y} ^ {2} y ^ {2} + {\ frac {1} {2}} m \ omega _ {z} ^ {2} z ^ {2}}$

é um sistema modelo com muitas aplicações na física moderna. A densidade de estados (ou mais precisamente, o grau de degeneração) para uma determinada espécie de spin é:

${\ displaystyle g (E) = {\ frac {E ^ {2}} {2 (\ hbar \ omega _ {\ text {ho}}) ^ {3}}} \ ,,}$

onde é a frequência de oscilação harmônica. ${\ displaystyle \ omega _ {\ text {ho}} = {\ sqrt [{3}] {\ omega _ {x} \ omega _ {y} \ omega _ {z}}}}$

A energia de Fermi para uma determinada espécie de spin é:

${\ displaystyle E _ {\ rm {F}} = (6N) ^ {1/3} \ hbar \ omega _ {\ text {ho}} \,}$

Quantidades de Fermi relacionadas

Relacionado à energia de Fermi, algumas quantidades úteis também ocorrem com frequência na literatura moderna.

A temperatura de Fermi é definida como , onde é a constante de Boltzmann . A temperatura de Fermi pode ser considerada como a temperatura na qual os efeitos térmicos são comparáveis ​​aos efeitos quânticos associados às estatísticas de Fermi. A temperatura de Fermi para um metal é algumas ordens de magnitude acima da temperatura ambiente. Outras quantidades definidas neste contexto são o momento de Fermi e a velocidade de Fermi , que são o momento e a velocidade do grupo , respectivamente, de um férmion na superfície de Fermi . O momento de Fermi também pode ser descrito como , onde é o raio da esfera de Fermi e é chamado de vetor de onda de Fermi . ${\ displaystyle T _ {\ mathrm {F}} = {\ frac {E _ {\ mathrm {F}}} {k _ {\ rm {B}}}}}$${\ displaystyle k _ {\ rm {B}}}$ ${\ displaystyle p _ {\ mathrm {F}} = {\ sqrt {2mE _ {\ mathrm {F}}}}}$ ${\ displaystyle v _ {\ mathrm {F}} = {\ frac {p _ {\ mathrm {F}}} {m}}}$${\ displaystyle p _ {\ mathrm {F}} = \ hbar k _ {\ mathrm {F}}}$${\ displaystyle k _ {\ mathrm {F}}}$

Observe que essas quantidades não são bem definidas nos casos em que a superfície de Fermi não é esférica.

Tratamento em temperatura finita

Grande conjunto canônico

A maioria dos cálculos acima são exatos na temperatura zero, mas permanecem como boas aproximações para temperaturas mais baixas do que a temperatura de Fermi. Para outras variáveis ​​termodinâmicas, é necessário escrever um potencial termodinâmico . Para um conjunto de férmions idênticos , a melhor maneira de derivar um potencial é a partir do grande conjunto canônico com temperatura, volume e potencial químico fixos µ . A razão é devido ao princípio de exclusão de Pauli, já que os números de ocupação de cada estado quântico são dados por 1 ou 0 (há um elétron ocupando o estado ou não), então a função de partição (grande) pode ser escrita como ${\ displaystyle {\ mathcal {Z}}}$

${\ displaystyle {\ mathcal {Z}} (T, V, \ mu) = \ sum _ {\ {q \}} e ^ {- \ beta (E_ {q} - \ mu N_ {q})} = \ prod _ {q} \ sum _ {n_ {q} = 0} ^ {1} e ^ {- \ beta (\ varepsilon _ {q} - \ mu) n_ {q}} = \ prod _ {q} \ left (1 + e ^ {- \ beta (\ varepsilon _ {q} - \ mu)} \ right),}$

onde , indexa os conjuntos de todos os microestados possíveis que dão a mesma energia total e número de partículas , é a energia de partícula única do estado (conta duas vezes se a energia do estado é degenerada) e , sua ocupação. Assim, o grande potencial é escrito como ${\ displaystyle \ beta ^ {- 1} = k _ {\ rm {B}} T}$${\ displaystyle \ {q \}}$${\ textstyle E_ {q} = \ sum _ {q} \ varepsilon _ {q} n_ {q}}$${\ textstyle N_ {q} = \ sum _ {q} n_ {q}}$${\ textstyle \ varepsilon _ {q}}$${\ textstyle q}$${\ textstyle n_ {q} = 0,1}$

${\ displaystyle \ Omega (T, V, \ mu) = - k _ {\ rm {B}} T \ ln \ left ({\ mathcal {Z}} \ right) = - k _ {\ rm {B}} T \ sum _ {q} \ ln \ left (1 + e ^ {\ beta (\ mu - \ varepsilon _ {q})} \ right)}$.

O mesmo resultado pode ser obtido no conjunto canônico e microcanônico , pois o resultado de cada conjunto deve dar o mesmo valor no limite termodinâmico . O grande conjunto canônico é recomendado aqui, pois evita o uso de combinatória e fatorial . ${\ textstyle (N / V \ rightarrow \ infty)}$

Conforme explorado nas seções anteriores, no limite macroscópico, podemos usar uma aproximação contínua (aproximação de Thomas-Fermi ) para converter essa soma em uma integral:

${\ displaystyle \ Omega (T, V, \ mu) = - k _ {\ rm {B}} T \ int _ {- \ infty} ^ {\ infty} D (\ varepsilon) \ ln (1 + e ^ { \ beta (\ mu - \ varepsilon)}) \, \ mathrm {d} \ varepsilon}$

onde D ( ε ) é a densidade total de estados.

Relação com a distribuição Fermi-Dirac

O grande potencial está relacionado ao número de partículas em temperatura finita da seguinte maneira

${\ displaystyle N = - \ left ({\ frac {\ partial \ Omega} {\ partial \ mu}} \ right) _ {T, V} = \ int _ {- \ infty} ^ {\ infty} D ( \ varejpsilon) {\ mathcal {f}} \ left ({\ frac {\ varepsilon - \ mu} {k _ {\ rm {B}} T}} \ right) \, \ mathrm {d} \ varepsilon}$

onde a derivada é obtida em temperatura e volume fixos, e parece

${\ displaystyle {\ mathcal {f}} (x) = {\ frac {1} {e ^ {x} +1}}}$

também conhecida como distribuição Fermi – Dirac .

Da mesma forma, a energia interna total é

${\ displaystyle U = \ Omega -T \ left ({\ frac {\ partial \ Omega} {\ partial T}} \ right) _ {V, \ mu} - \ mu \ left ({\ frac {\ partial \ Omega} {\ partial \ mu}} \ right) _ {T, V} = \ int _ {- \ infty} ^ {\ infty} D (\ varepsilon) {\ mathcal {f}} \ left ({\ frac {\ varejpsilon - \ mu} {k _ {\ rm {B}} T}} \ right) \ varejpsilon \, \ mathrm {d} \ varejpsilon.}$

Solução exata para densidade de estados de lei de potência

Curvas de entropia vs temperatura de gás ideal clássico e gases ideais quânticos (gás Fermi, gás de Bose ) em três dimensões ( α = 1,5) com N , V constante .

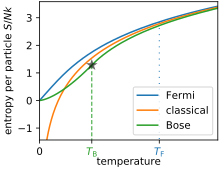
Muitos sistemas de interesse têm uma densidade total de estados com a forma de lei de potência:

${\ displaystyle D (\ varepsilon) = Vg (\ varepsilon) = {\ frac {Vg_ {0}} {\ Gamma (\ alpha)}} (\ varepsilon - \ varepsilon _ {0}) ^ {\ alpha -1 }, \ qquad \ varepsilon \ geq \ varepsilon _ {0}}$

para alguns valores de g ₀ , α , ε ₀ . Os resultados das seções anteriores generalizam para dimensões d , dando uma lei de potência com:

• α = d / 2 para partículas não relativísticas em umacaixa d- dimensional,
• α = d para partículas não relativísticas em umpoço de potencial harmônico d- dimensional,
• α = d para partículas hiper-relativísticas em umacaixa d- dimensional.

Para tal densidade de lei de potência de estados, o grande potencial integral avalia exatamente para:

${\ displaystyle \ Omega (T, V, \ mu) = - Vg_ {0} (k _ {\ rm {B}} T) ^ {\ alpha +1} F _ {\ alpha} \ left ({\ frac {\ mu - \ varepsilon _ {0}} {k _ {\ rm {B}} T}} \ right),}$

onde é a integral de Fermi – Dirac completa (relacionada ao polilogaritmo ). A partir desse grande potencial e seus derivados, todas as quantidades termodinâmicas de interesse podem ser recuperadas. ${\ displaystyle F _ {\ alpha} (x)}$

Extensões ao modelo

Gás de Fermi relativístico

Relações raio-massa para um modelo de anã branca, relação relativística vs não relativística. O limite de Chandrasekhar é indicado como M _Ch .

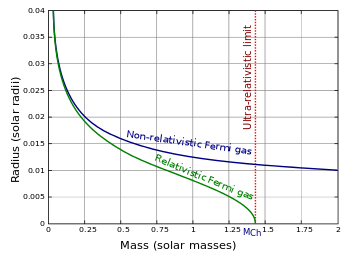
O artigo tratou apenas do caso em que as partículas têm uma relação parabólica entre energia e momento, como é o caso da mecânica não relativística. Para partículas com energias próximas de suas respectivas massas de repouso , as equações da relatividade especial são aplicáveis. Onde a energia de uma única partícula é dada por:

${\ displaystyle E = {\ sqrt {(pc) ^ {2} + (mc ^ {2}) ^ {2}}}}$.

Para este sistema, a energia Fermi é dada por:

${\ displaystyle E _ {\ mathrm {F}} = {\ sqrt {(p _ {\ mathrm {F}} c) ^ {2} + (mc ^ {2}) ^ {2}}} - mc ^ {2 } \ approx p _ {\ mathrm {F}} c}$,

onde a igualdade só é válida no limite ultrarelativístico , e ${\ displaystyle \ aprox}$

${\ displaystyle p _ {\ mathrm {F}} = \ hbar \ left ({\ frac {1} {g_ {s}}} 6 \ pi ^ {2} {\ frac {N} {V}} \ right) ^ {1/3}}$.

O modelo relativístico do gás Fermi também é usado para a descrição de grandes anãs brancas que estão perto do limite de Chandresekhar. Para o caso ultrarelativístico, a pressão de degenerescência é proporcional a . ${\ displaystyle (N / V) ^ {4/3}}$

Líquido Fermi

Em 1956, Lev Landau desenvolveu a teoria do líquido de Fermi , onde tratou o caso de um líquido de Fermi, ou seja, um sistema com interações repulsivas, não necessariamente pequenas, entre férmions. A teoria mostra que as propriedades termodinâmicas de um gás Fermi ideal e de um líquido Fermi não diferem muito. Pode-se mostrar que o líquido de Fermi é equivalente a um gás de Fermi composto de excitações coletivas ou quasipartículas , cada uma com uma massa efetiva e momento magnético diferentes .

Veja também

• Gás Bose
• Condensado fermiônico
• Gás em uma caixa
• Gelatina
• Gás eletrônico bidimensional

Referências

Leitura adicional

• Neil W. Ashcroft e N. David Mermin , Solid State Physics (Harcourt: Orlando, 1976).
• Charles Kittel , Introdução à Física do Estado Sólido , 1ª ed. 1953 - 8ª ed. 2005, ISBN  0-471-41526-X