Teoria supersimétrica da dinâmica estocástica - Supersymmetric theory of stochastic dynamics

${\ displaystyle \ textstyle {\ hat {L}}}$

${\ textstyle {\ hat {\ triangle}}}$

${\ displaystyle \ textstyle {\ hat {d}} = \ chi ^ {i} \ parcial / \ parcial x ^ {i}}$

${\ displaystyle \ textstyle {\ hat {\ bar {d}}} = - (i {\ hat {\ bar {\ chi}}} _ {i}) \ delta ^ {ij} (\ partial _ {j} U + \ Theta (i {\ hat {B}} _ {j}))}$

${\ displaystyle i {\ hat {B}} _ {j} = \ parcial / \ parcial x ^ {j}}$

${\ displaystyle i {\ hat {\ bar {\ chi}}} _ {j} = \ parcial / \ parcial \ chi ^ {j}}$

${\ displaystyle \ chi}$

${\ displaystyle {\ hat {\ bar {\ chi}}}}$

${\ displaystyle \ textstyle {\ hat {\ bar {d}}}}$

${\ displaystyle {\ hat {d}} ^ {2} = 0}$

${\ displaystyle \ textstyle {\ hat {\ bar {d}}}}$

Espaço Hilbert

As funções de onda são funções não apenas das variáveis ​​bosônicas , mas também dos

${\ displaystyle x \ in X}$

${\ displaystyle \ chi \ in TX}$

${\ displaystyle X}$

${\ displaystyle X}$

${\ displaystyle \ chi \ equiv dx \ wedge}$

${\ displaystyle X}$

Relação com o modelo sigma não linear e topologia algébrica

Na Ref., Foi introduzido um modelo que pode ser visto como um protótipo 1D dos modelos sigma não lineares topológicos (TNSM), uma subclasse das teorias de campo topológico do tipo Witten . O 1D TNSM é definido para espaços de fase Riemannianos, enquanto para espaços de fase euclidianos se reduz ao modelo Parisi-Sourlas. Sua principal diferença em relação ao STS é o operador de difusão, que é o Hodge Laplacian para 1D TNSM e para STS. Esta diferença não é importante no contexto da relação entre STS e topologia algébrica, a relação estabelecida pela teoria de 1D TNSM (ver, por exemplo, Refs.). ${\ displaystyle \ textstyle {\ hat {L}} _ {e_ {a}} {\ hat {L}} _ {e_ {a}}}$

O modelo é definido pela seguinte operador de evolução , onde com sendo a métrica, é a

${\ textstyle {\ hat {H}} = {\ hat {L}} _ {- \ U parcial} + \ Theta [{\ hat {d}}, {\ hat {d}} ^ {\ punhal}] }$

${\ textstyle (\ parcial U) ^ {i} = g ^ {ij} \ parcial _ {j} U}$

${\ textstyle g}$

${\ textstyle [{\ hat {d}}, {\ hat {d}} ^ {\ dagger}]}$

${\ textstyle \ Omega (X)}$

${\ displaystyle {\ hat {H}} \ to {\ hat {H}} _ {U} = e ^ {U / 2 \ Theta} {\ hat {H}} e ^ {- U / 2 \ Theta} }$

${\ displaystyle {\ hat {H}} _ {U} = \ Theta [{\ hat {d}} _ {U}, {\ hat {d}} _ {U} ^ {\ dagger}]}$

${\ displaystyle {\ hat {d}} _ {U} = e ^ {U / 2 \ Theta} {\ hat {d}} e ^ {- U / 2 \ Theta} = \ chi ^ {i} (\ parcial / \ parcial x ^ {i} - \ parcial _ {i} U / 2 \ Theta)}$

${\ displaystyle {\ hat {H}} _ {U}}$

${\ displaystyle {\ hat {q}} _ {1} = ({\ hat {d}} _ {U} + {\ hat {d}} _ {U} ^ {\ dagger}) / 2 ^ {1 / 2}}$

${\ displaystyle {\ hat {q}} _ {2} = i ({\ hat {d}} _ {U} - {\ hat {d}} _ {U} ^ {\ dagger}) / 2 ^ { 1/2}}$

${\ displaystyle {\ hat {H}} _ {U} = \ Theta {\ hat {q}} _ {1} ^ {2} = \ Theta {\ hat {q}} _ {2} ^ {2} }$

${\ displaystyle {\ hat {H}} _ {U}}$

${\ displaystyle {\ hat {H}}}$

As seguintes propriedades do operador de evolução de 1D TNSM valem até mesmo para o SEO dos SDEs de forma arbitrária. O operador de evolução comuta com o operador do grau de formas diferenciais. Como resultado, onde e é o espaço das formas diferenciais de grau . Além disso, devido à presença de TS ,, onde estão os autoestados supersimétricos,, não triviais na

${\ displaystyle \ textstyle {\ hat {H}} = {\ hat {H}} ^ {(\ dim X)} \ oplus \ dots \ oplus {\ hat {H}} ^ {(0)}}$

${\ displaystyle \ textstyle {\ hat {H}} ^ {(k)} = {\ hat {H}} | _ {\ Omega ^ {(k)}}}$

${\ displaystyle \ Omega ^ {(n)} (X)}$

${\ displaystyle n}$

${\ textstyle \ Omega (X) = {\ mathcal {H}} \ oplus {\ mathcal {N}} \ oplus ({\ hat {d}} {\ mathcal {N}})}$

${\ textstyle {\ mathcal {H}}}$

${\ textstyle \ theta 's}$

${\ textstyle | \ vartheta \ rangle}$

${\ textstyle {\ hat {d}} | \ vartheta \ rangle}$

${\ textstyle {\ mathcal {W}} = \ # \ {{\ text {par}} \ theta 's \} - \ # \ {{\ text {ímpar}} \ theta' s \}.}$

${\ displaystyle X}$

Procedimento BRST para SDEs de forma arbitrária

O método Parisi-Sourlas de abordagem do procedimento BRST para Langevin SDEs também foi adaptado para a mecânica clássica, generalização estocástica da mecânica clássica, Langevin SDEs de ordem superior e, mais recentemente, para SDEs de forma arbitrária. Embora existam técnicas padrão que permitem considerar modelos com ruídos coloridos, "espaços de base" de dimensão superior descritos por SDEs parciais, etc., os elementos-chave do STS podem ser discutidos usando a seguinte classe básica de SDEs,

$${\ displaystyle {\ dot {x}} (t) = F (x (t)) + (2 \ Theta) ^ {1/2} e_ {a} (x (t)) \ xi ^ {a} ( t),}$$

${\ textstyle x \ in X}$

${\ displaystyle F (x) \ in TX_ {x}}$

${\ displaystyle X}$

${\ displaystyle e_ {a} \ in TX, a = 1, \ ldots, \ dim X}$

${\ displaystyle e_ {a}}$

${\ displaystyle X}$

Ambiguidade da representação integral do caminho e o dilema de Ito-Stratonovich

O procedimento de fixação do medidor BRST segue as mesmas linhas do caso de Langevin SDEs. A interpretação topológica do procedimento BRST é a mesma e a representação integral do caminho do índice de Witten é definida pelo férmion de calibre , dado pela mesma expressão, mas com a versão generalizada de . Há uma sutileza importante, no entanto, que aparece no caminho para a representação do operador do modelo. Ao contrário dos SDEs de Langevin, da mecânica clássica e de outros SDEs com ruídos aditivos, a representação integral do caminho do SEO de tempo finito é um objeto ambíguo. Essa ambigüidade se origina da não comutatividade dos operadores de momento e posição, por exemplo ,. Como resultado, no caminho a representação integral tem toda uma família de um parâmetro de possíveis interpretações na representação do operador,, onde denota uma função de onda arbitrária. Assim, existe toda uma família de SEOs infinitesimais, ${\ displaystyle \ textstyle \ Psi}$${\ textstyle \ textstyle {\ bar {d}} = \ imath _ {F} - \ Theta \ imath _ {e_ {a}} (Q, \ imath _ {e_ {a}})}$${\ displaystyle {\ hat {B}} {\ hat {x}} \ neq {\ hat {x}} {\ hat {B}}}$${\ displaystyle B (\ tau) x (\ tau)}$${\ displaystyle (\ alpha {\ hat {B}} {\ hat {x}} + (1- \ alpha) {\ hat {x}} {\ hat {B}}) | \ psi (\ tau) \ rangle}$${\ displaystyle | \ psi (\ tau) \ rangle}$${\ displaystyle \ alpha}$

$${\ displaystyle {\ hat {H}} _ {\ alpha} = {\ hat {L}} _ {F} - \ Theta {\ hat {L}} _ {e_ {a}} {\ hat {L} } _ {e_ {a}} = [{\ hat {d}}, {\ hat {\ bar {d}}} _ {\ alpha}],}$$

${\ displaystyle \ textstyle {\ hat {\ bar {d}}} _ {\ alpha} = {\ hat {\ imath}} _ {F _ {\ alpha}} - \ Theta {\ hat {\ imath}} _ {e_ {a}} {\ hat {L}} _ {e_ {a}}}$

${\ displaystyle {\ hat {\ imath}} _ {F _ {\ alpha}}}$

${\ displaystyle \ textstyle F _ {\ alpha} = F- \ Theta (2 \ alpha -1) (e_ {a} \ cdot \ parcial) e_ {a}}$

${\ displaystyle {\ hat {\ bar {d}}} _ {\ alpha}}$

A representação integral do caminho da dinâmica estocástica é equivalente ao entendimento tradicional de SDEs como um limite de tempo contínuo de equações de diferenças estocásticas onde diferentes escolhas de parâmetros são chamadas de "interpretações" de SDEs. A escolha , para a qual e que é conhecida na teoria quântica como regra de

${\ displaystyle \ alpha}$

${\ displaystyle \ alpha = 1/2}$

${\ displaystyle \ textstyle F_ {1/2} = F}$

${\ displaystyle \ alpha = 1}$

Eigensistema de operador de evolução estocástica

Os três tipos possíveis de espectros de SEO em uma esfera 3D. Cada linha de triplos de gráficos representa . para os três tipos de espectros. Os pontos pretos na origem da primeira e da última linha representam autoestados supersimétricos do zero e da terceira cohomologia da 3 esfera. Para os tipos B e C , o (crescimento mais rápido) terra (Eigen) estados são não-supersimétrica porque eles têm diferentes de zero valores próprios. TS é quebrado espontaneamente. As linhas verticais com setas visualizam o operador de supersimetria.${\ displaystyle spec {\ hat {H}} ^ {(n)},}$ ${\ displaystyle n = 0, ... 3}$

Em comparação com o SEO de Langevin SDEs, o SEO de uma forma geral de SDE é pseudo-hermitiano. Como resultado, os valores próprios de estados próprios não supersimétricos não são restritos a serem positivos reais, enquanto os valores próprios de estados próprios supersimétricos ainda são exatamente zero. Assim como para os SDEs de Langevin e o modelo sigma não linear, a estrutura do auto-sistema do SEO restabelece o caráter topológico do índice de Witten: as contribuições dos pares não supersimétricos de autoestados desaparecem e apenas os estados supersimétricos contribuem com a característica de

${\ displaystyle X}$

${\ displaystyle \ textstyle {\ hat {H}} ^ {(\ operatorname {dim} X)}}$

${\ displaystyle \ textstyle {\ hat {H}} ^ {(0)}}$

${\ displaystyle \ textstyle Re (\ operatorname {spec} {\ hat {H}} ^ {(\ operatorname {dim} X)}) \ geq 0}$

STS sem procedimento BRST

O significado matemático do operador de evolução estocástica

O SEO de tempo finito pode ser obtido de outra forma, mais matemática, a partir da ideia de estudar diretamente as ações induzidas por SDE em formas diferenciais, sem passar pelo procedimento de fixação de bitola BRST. O assim obtido SEO de tempo finito é conhecido na teoria de sistemas dinâmicos como o operador de transferência generalizado e também tem sido usado na teoria clássica de SDEs (ver, por exemplo, Refs.). A contribuição do STS para essa construção é a exposição da estrutura supersimétrica subjacente e o estabelecimento de sua relação com o procedimento BRST para SDEs.

Ou seja, para qualquer configuração do ruído,, e uma condição inicial ,, SDE define uma solução / trajetória única ,. Mesmo para configurações de ruído não diferenciáveis ​​em relação ao tempo , a solução é diferenciável em relação à condição inicial . Em outras palavras, SDE define a família dos

${\ displaystyle \ xi}$

${\ displaystyle x (t ') = x' \ em X}$

${\ displaystyle x (t) \ in X}$

${\ displaystyle t}$

${\ displaystyle x '}$

${\ displaystyle M_ {tt '}: X \ a X}$

${\ displaystyle x (t) = M_ {tt '} (x')}$

${\ displaystyle \ textstyle M_ {t't} ^ {*}: \ Omega (X) \ to \ Omega (X)}$

${\ displaystyle X}$

${\ displaystyle X}$

${\ displaystyle M_ {t't} ^ {*}}$

${\ displaystyle \ xi}$

${\ displaystyle {\ hat {\ mathcal {M}}} _ {tt '} = \ langle M_ {t't} ^ {*} \ rangle _ {\ text {noise}} = e ^ {- (t- t ') {\ hat {H}} _ {1/2}}}$

Dentro desta definição de SEO de tempo finito, o índice de Witten pode ser reconhecido como o traço nítido do operador de transferência generalizado. É também liga o índice Witten para o índice teorema , , uma constante topológica que é igual a

${\ textstyle \ textstyle I_ {L} = \ operatorname {Tr} (-1) ^ {\ hat {n}} M_ {t't} ^ {*} = \ sum _ {x \ in \ operatorname {fix} M_ {tt '}} \ operatorname {sinal} \ operatorname {det} (\ delta _ {j} ^ {i} - \ parcial M_ {tt'} ^ {i} (x) / \ parcial x ^ {j} )}$

${\ textstyle \ textstyle {\ mathcal {W}} = \ operatorname {Tr} (-1) ^ {\ hat {n}} \ langle M_ {t't} ^ {*} \ rangle _ {\ text {ruído }} = \ langle \ operatorname {Tr} (-1) ^ {\ hat {n}} M_ {t't} ^ {*} \ rangle _ {\ text {ruído}} = I_ {L}}$

O significado da supersimetria e o efeito borboleta

A supersimetria N = 2 de Langevin SDEs foi associada ao princípio Onsager de reversibilidade microscópica e igualdade de Jarzynski . Na mecânica clássica, foi proposta uma relação entre a supersimetria N = 2 correspondente e a ergodicidade . Em SDEs de forma geral, onde os argumentos físicos podem não ser aplicáveis, uma explicação de nível inferior do TS está disponível. Esta explicação é baseada na compreensão do SEO de tempo finito como um retrocesso estocasticamente calculado dos difeomorfismos definidos pelo SDE (consulte a subseção acima). Nesta imagem, a questão de por que qualquer SDE tem TS é a mesma que a questão de por que a derivada externa comuta com o retrocesso de qualquer difeomorfismo. A resposta a esta pergunta é a diferenciabilidade do mapa correspondente. Em outras palavras, a presença de TS é a versão algébrica da afirmação de que o fluxo em tempo contínuo preserva a continuidade de . Dois pontos inicialmente próximos permanecerão próximos durante a evolução, o que é apenas outra maneira de dizer que é um difeomorfismo. ${\ displaystyle X}$${\ displaystyle M_ {tt '}}$

Em modelos caóticos determinísticos, pontos inicialmente próximos podem fazer parte do limite da evolução temporal infinitamente longa. Este é o famoso efeito borboleta , que equivale à afirmação de que perde a diferenciabilidade neste limite. Na representação algébrica da dinâmica, a evolução no limite de tempo infinitamente longo é descrita pelo estado fundamental do SEO e o efeito borboleta é equivalente à quebra espontânea do TS, ou seja, à situação em que o estado fundamental não é supersimétrico. Digno de nota, ao contrário do entendimento tradicional da dinâmica caótica determinística, a quebra espontânea de TS funciona também para casos estocásticos. Esta é a generalização mais importante porque a dinâmica determinística é, de fato, uma idealização matemática. Os sistemas dinâmicos reais não podem ser isolados de seus ambientes e, portanto, sempre experimentam influência estocástica. ${\ displaystyle M_ {tt '}}$

Quebra de supersimetria espontânea e caos dinâmico

O procedimento de fixação do medidor BRST aplicado aos SDEs leva diretamente ao índice de Witten. O índice de Witten é de caráter topológico e não responde a nenhuma perturbação. Em particular, todos os correlacionadores de resposta calculados usando o índice de Witten desaparecem. Este fato tem uma interpretação física dentro do STS: o significado físico do índice de Witten é a função de partição do ruído e como não há retrocesso do sistema dinâmico para o ruído, o índice de Witten não possui informações sobre os detalhes do SDE . Em contraste, as informações sobre os detalhes do modelo estão contidas no outro objeto semelhante a um traço da teoria, a função de partição dinâmica,

$${\ displaystyle {\ mathcal {Z}} _ {tt '} = \ int \ dots \ int _ {apbc} e ^ {(Q, \ Psi)} D \ Phi = \ operatorname {Tr} {\ hat {\ matemática {M}}} _ {tt '},}$$

Para uma ampla classe de modelos, a função de partição dinâmica fornece limite inferior para o número médio estocástico de pontos fixos dos difeomorfismos definidos por SDE,

$${\ displaystyle \ left. {\ mathcal {Z}} _ {tt '} \ right | _ {t-t' \ to \ infty} = \ sum \ nolimits _ {p} e ^ {- (t-t ' ) {\ mathsf {E}} _ {p}} \ leq \ langle \ # \ {{\ text {pontos fixos de}} M_ {t't} \} \ rangle _ {\ text {ruído}} \ propto e ^ {(t-t ') S}.}$$

${\ displaystyle p}$

${\ textstyle \ Gamma _ {g} = - \ min _ {\ alpha} \ operatorname {Re} {\ mathsf {E}} _ {\ alpha} \ geq 0}$

${\ displaystyle S}$

${\ displaystyle \ Gamma _ {g}}$

${\ displaystyle 0 <\ Gamma _ {g} \ leq S}$

${\ displaystyle \ Gamma _ {g}}$

A lista completa de razões pelas quais a quebra espontânea de TS deve ser vista como a generalização estocástica do conceito de caos dinâmico é a seguinte.

• Entropia dinâmica positiva.
• De acordo com o teorema de Goldstone , a quebra espontânea de TS deve ajustar um comportamento dinâmico de longo alcance, uma das manifestações do qual é o efeito borboleta discutido acima no contexto do significado de TS.
• A partir das propriedades do autossistema de SEO, o TS pode ser quebrado espontaneamente somente se . Esta conclusão pode ser vista como a generalização estocástica do teorema de

${\ displaystyle F}$

Todos os recursos de quebra de TS acima funcionam para modelos determinísticos e estocásticos. Isso está em contraste com o caos determinístico tradicional cujas propriedades baseadas na trajetória, como a mistura topológica, não podem, em princípio, ser generalizadas para o caso estocástico porque, assim como na dinâmica quântica, todas as trajetórias são possíveis na presença de ruído e, digamos, o a propriedade de mistura é satisfeita trivialmente por todos os modelos com intensidade de ruído diferente de zero.

STS como uma teoria de campo topológico

O quadrado acbd representa um instanton, ou seja, a família de trajetórias de fluxo determinístico (curvas pontilhadas com setas) que vão de um ponto crítico (b) a outro (a). O bra / ket ( / ) dos estados fundamental localmente supersimétricos (vacua) correspondentes a esses pontos críticos são os duais de Poincaré das variedades locais instáveis ​​/ estáveis. Os operadores são Poincare duals de linhas verticais / horizontais. O valor do elemento da matriz instantânea é o número da interseção (a diferença nos números das interseções positivas (pretas) e negativas (brancas)). É invariante sob a evolução temporal devido ao fluxo ,.${\ displaystyle \ langle a |}$${\ displaystyle | b \ rangle}$${\ displaystyle {\ hat {O}} _ {1,2}}$${\ displaystyle {\ hat {O}} _ {1} (0) \ to {\ hat {O}} _ {1} (t)}$

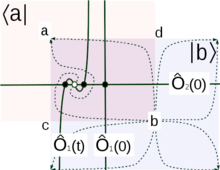
O setor topológico do STS pode ser reconhecido como um membro das teorias de campo topológico do tipo Witten . Em outras palavras, alguns objetos no STS são de caráter topológico, sendo o índice de Witten o exemplo mais famoso. Existem outras classes de objetos topológicos. Uma classe de objetos está relacionada a instantons , ou seja, dinâmica transitória. Papel amassado, dobramento de proteína e muitos outros processos dinâmicos não lineares em resposta a quenches, ou seja, a mudanças externas (repentinas) de parâmetros, podem ser reconhecidos como dinâmica instantânea. Do ponto de vista matemático, instantons são famílias de soluções de equações determinísticas de movimento , que vão desde, digamos, um ponto fixo menos estável até um ponto fixo mais estável. Certos elementos de matriz calculados em instantons são de natureza topológica. Um exemplo de tais elementos de matriz pode ser definido para um par de pontos críticos e , por ser mais estável do que ,${\ displaystyle {\ dot {x}} = F}$${\ displaystyle F}$${\ displaystyle a}$${\ displaystyle b}$${\ displaystyle a}$${\ displaystyle b}$

$${\ displaystyle \ left. \ int \ dots \ int _ {x (\ pm \ infty) = a, b} \ left (\ prod \ nolimits _ {i} O_ {i} (t_ {i}) \ right) e ^ {({\ mathcal {Q}}, \ Psi)} D \ Phi \ right | _ {\ Theta \ to 0} = \ langle a | {\ mathcal {T}} \ left (\ prod \ nolimits _ {i} {\ hat {O}} _ {i} (t_ {i}) \ right) | b \ rangle.}$$

${\ displaystyle \ langle a |}$

${\ displaystyle | b \ rangle}$

${\ displaystyle {\ mathcal {T}}}$

${\ displaystyle O}$

${\ displaystyle X}$

${\ displaystyle {\ hat {O}} (t) = {\ hat {\ mathcal {M}}} _ {t_ {0}, t} {\ hat {O}} {\ hat {\ mathcal {M} }} _ {t, t_ {0}}}$

${\ displaystyle t_ {0}}$

${\ displaystyle | a \ rangle}$

${\ displaystyle | b \ rangle}$

${\ displaystyle t_ {i} 's}$

${\ displaystyle O}$

Os elementos da matriz instantânea acima são exatos apenas no limite determinístico. No caso estocástico geral, pode-se considerar estados supersimétricos globais, 's, das classes de

${\ displaystyle \ theta}$

${\ displaystyle X}$

${\ displaystyle \ gamma}$

${\ displaystyle X}$

${\ displaystyle \ textstyle \ langle \ theta _ {\ alpha} | {\ mathcal {T}} \ left (\ prod \ nolimits _ {i} {\ hat {\ gamma}} _ {i} (t_ {i} ) \ right) | \ theta _ {\ beta} \ rangle,}$

${\ displaystyle X}$

Formulários

A teoria supersimétrica da dinâmica estocástica pode ser interessante de diferentes maneiras. Por exemplo, o STS oferece uma realização promissora do conceito de supersimetria . Em geral, existem dois problemas principais no contexto da supersimetria. O primeiro é estabelecer conexões entre essa entidade matemática e o mundo real. Dentro do STS, a supersimetria é a simetria mais comum na natureza porque é pertinente a todos os sistemas dinâmicos de tempo contínuo. O segundo é o colapso espontâneo da supersimetria . Este problema é particularmente importante para a física de partículas porque a supersimetria de partículas elementares , se existir em escala extremamente curta, deve ser quebrada espontaneamente em grande escala. Esse problema não é trivial porque as supersimetrias são difíceis de quebrar espontaneamente, a própria razão por trás da introdução da quebra de supersimetria suave ou explícita . Dentro do STS, o colapso espontâneo da supersimetria é de fato um fenômeno dinâmico não trivial que tem sido conhecido de várias maneiras nas disciplinas como caos , turbulência , criticidade auto-organizada etc.

Algumas aplicações mais específicas do STS são as seguintes.

Classificação da dinâmica estocástica

Os sistemas dinâmicos estocásticos podem ser classificados de acordo com se o TS é quebrado espontaneamente ou não (ordenado / simétrico) e se o campo vetorial de fluxo é integrável ou não integrável (às vezes caótico). A fase simétrica pode ser identificada como equilíbrio térmico (T). A fase ordenada não integrável pode ser chamada de caos (C) porque hospeda o caos determinístico convencional. A fase integrável ordenada pode ser chamada de caos induzido por ruído (N) porque a quebra de TS envolve anti-instantons que desaparecem no limite determinístico. A N - fase também é conhecido na literatura como criticalidade auto-organizada.

O STS fornece classificação para modelos estocásticos dependendo se o TS está quebrado e da integrabilidade do campo vetorial de fluxo. Pode ser exemplificado como uma parte do diagrama de fase geral na fronteira do caos (veja a figura à direita). O diagrama de fases possui as seguintes propriedades:

• Para modelos físicos, o TS é restaurado eventualmente com o aumento da intensidade do ruído.
• A fase simétrica pode ser chamada de equilíbrio térmico ou fase T porque o estado fundamental é o estado supersimétrico da distribuição de probabilidade total de estado estacionário.
• No limite determinístico, a fase ordenada é equivalente à dinâmica caótica determinística com fluxo não integrável.
• A fase ordenada não integrável pode ser chamada de caos ou fase C porque o caos determinístico comum pertence a ela.
• A fase integrável ordenada pode ser chamada de caos induzido por ruído ou fase N porque desaparece no limite determinístico. O TS é interrompido pela condensação de (anti-) instantons (veja abaixo).
• Em ruídos mais fortes, o limite NC nítido deve se espalhar em um cruzamento porque (anti) instantons perdem sua individualidade e é difícil para um observador externo distinguir um processo de tunelamento de outro.

Desmistificação da criticidade auto-organizada

Muitos processos repentinos (ou instantâneos) na natureza, como, por exemplo, ruído crepitante , exibem estatísticas sem escala, freqüentemente chamadas de lei de Zipf . Como explicação para esse comportamento dinâmico espontâneo peculiar, foi proposto acreditar que alguns sistemas dinâmicos estocásticos tendem a se auto-sintonizar em um ponto crítico , a abordagem fenomenológica conhecida como criticidade auto-organizada (SOC). STS oferece uma perspectiva alternativa sobre este fenômeno. Dentro do STS, SOC nada mais é do que dinâmica na fase N. Especificamente, a característica definitiva da fase N é o mecanismo peculiar de quebra do TS. Ao contrário da fase C, onde o TS é rompido pela não integrabilidade do escoamento, na fase N , o TS é rompido espontaneamente devido à condensação das configurações de instantons e antiinstantons induzidos por ruído, ou seja, tempo - instantons revertidos. Esses processos podem ser interpretados grosso modo como os eventos de tunelamento induzidos por ruído entre, por exemplo, atratores diferentes. Qualitativamente, a dinâmica na fase N aparece para um observador externo como uma sequência de saltos repentinos ou "avalanches" que devem exibir um comportamento / estatística sem escala como resultado do teorema de Goldstone . Esta imagem da dinâmica na fase N é exatamente o comportamento dinâmico que o conceito de SOC foi projetado para explicar. Em contraste com o entendimento original do SOC, sua interpretação STS tem pouco a ver com a teoria dos fenômenos críticos tradicionais

Teoria cinemática do dínamo

O fenômeno magnetohidrodinâmico do dínamo cinemático também pode ser identificado como a quebra espontânea da ST. Este resultado decorre da equivalência entre o operador de evolução do campo magnético e o SEO da SDE correspondente que descreve o fluxo da matéria de fundo. A assim emergida correspondência STS-dínamo cinemático prova, em particular, que ambos os tipos de espectros de quebra de TS são possíveis, com os autovalores reais e complexos do estado fundamental, porque o dínamo cinemático com ambos os tipos de autovalores de crescimento mais rápido são conhecidos.

Dinâmica transitória

É bem conhecido que vários tipos de dinâmica transitória, como quenches, exibem comportamento espontâneo de longo alcance. No caso de quenches em transições de fase, esse comportamento é frequentemente atribuído à proximidade de criticidade. As têmpera que não exibem uma transição de fase também são conhecidas por exibirem características de longo alcance, com os exemplos mais conhecidos sendo o efeito Barkhausen e as várias realizações do conceito de ruído crepitante . É intuitivamente atraente que as explicações teóricas para o comportamento sem escala em quenches devam ser as mesmas para todos os quenches, independentemente de produzir ou não uma transição de fase; STS oferece essa explicação. A saber, a dinâmica transiente é essencialmente um instanton composto e o TS é intrinsecamente quebrado dentro dos instantons. Embora a quebra de TS dentro de instantons não seja exatamente devido ao fenômeno da quebra espontânea de uma simetria por um estado fundamental global, essa quebra de TS efetiva também deve resultar em um comportamento sem escala. Esse entendimento é apoiado pelo fato de que instantons condensados ​​levam ao aparecimento de logaritmos nas funções de correlação. Esta imagem da dinâmica transitória explica a eficiência computacional das máquinas de computação digital.

Teorias eficazes de baixa energia para o caos dinâmico

Em física, a quebra espontânea de simetria é conhecida como "ordenação". Por exemplo, a quebra espontânea da simetria translacional em um líquido é a essência matemática da cristalização ou "ordenação" espacial das moléculas em uma rede. Portanto, a imagem de quebra de TS espontânea da dinâmica caótica é, em certo sentido, oposta à semântica da palavra "caos". Devido ao seu caráter temporal, é na verdade Chronos , não Caos , que parece ser a divindade grega primordial mais próxima em seu espírito da ordem de quebra da ST. Talvez, um identificador mais preciso do que "caos" deva ser cunhado para a quebra de TS no futuro. A partir deste momento, essa compreensão qualitativamente nova do caos dinâmico já aponta para uma direção de pesquisa que pode levar à resolução de alguns problemas importantes, como turbulência e neurodinâmica. Nomeadamente, como no caso de qualquer outra "ordenação", uma descrição simplificada mas precisa da dinâmica caótica pode ser alcançada em termos da teoria efetiva de baixa energia para um parâmetro de ordem . Embora a descrição efetiva de baixa energia da dinâmica caótica possa ser muito específica para o caso, seu parâmetro de ordem deve sempre ser um representante dos férmions ou goldstinos sem intervalos do TS espontaneamente quebrado.

Veja também

• Quantização estocástica

Referências