Notação vetorial - Vector notation

Notação vetorial

Seta vetorial
apontando de A para B

Os componentes do vector
que descreve uma seta vetor v pelas suas coordenadas x e y produz um isomorfismo de espaço vectorial.

Produto escalar
Duas sequências de tamanhos iguais de vetores de coordenadas e retorna um único número

Produto vetorial
O produto cruzado em relação a um sistema de coordenadas para destros

Em matemática e física , notação vectorial é um comumente usados notação para representam vectores , que podem ser vectores geométricas , ou, mais geralmente, membros de um espaço vectorial .

Para representar um vetor, a convenção tipográfica comum é minúscula, tipo em negrito vertical, como em v . A International Organization for Standardization (ISO) recomenda serifa itálico em negrito, como em v , ou serifa itálico não negrito acentuada por uma seta para a direita, como em . ${\ displaystyle {\ vec {v}}}$

Em matemática avançada, os vetores são frequentemente representados em itálico simples, como qualquer variável .

História

O conceito de vetor foi cunhado por WR Hamilton por volta de 1843, quando ele revelou quatérnios , um sistema que usa vetores e escalares para abranger um espaço quadridimensional. Para um quatérnio q = a + b i + c j + d k, Hamilton usou duas projeções: S q = a , para a parte escalar de q , e V q = b i + c j + d k, a parte do vetor. Usando os termos modernos produto cruzado (×) e produto escalar (.), O produto quaternário de dois vetores p e q pode ser escrito pq = - p . q + p × q . Em 1878, WK Clifford separou os dois produtos para tornar a operação do quaternion útil para os alunos em seu livro Elements of Dynamic . Como palestrante na Universidade de Yale , Josiah Willard Gibbs forneceu notação para o produto escalar e produtos vetoriais , que foi introduzido na análise vetorial .

Em 1891, Oliver Heaviside defendeu Clarendon para distinguir vetores de escalares. Ele criticou o uso de letras gregas por Tait e letras góticas por Maxwell.

Em 1912, JB Shaw contribuiu com seu "Comparative Notation for Vector Expressions" para o Bulletin of the Quaternion Society . Posteriormente, Alexander Macfarlane descreveu 15 critérios para expressão clara com vetores na mesma publicação.

As ideias de vetor foram desenvolvidas por Hermann Grassmann em 1841 e novamente em 1862 na língua alemã . Mas os matemáticos alemães não gostavam tanto dos quatérnios quanto os matemáticos de língua inglesa. Quando Felix Klein estava organizando a enciclopédia matemática alemã , ele designou Arnold Sommerfeld para padronizar a notação vetorial. Em 1950, quando a Academic Press publicou a tradução de G. Kuerti da segunda edição do volume 2 de Lectures on Theoretical Physics de Sommerfeld, a notação vetorial foi o assunto de uma nota de rodapé: "No texto original em alemão, os vetores e seus componentes são impressos no mesmos tipos góticos. A maneira mais comum de fazer uma distinção tipográfica entre os dois foi adotada para esta tradução. "

Vetores retangulares

Retângulo

Cuboide retangular

Um vetor retangular é um vetor de coordenadas especificado por componentes que definem um retângulo (ou prisma retangular em três dimensões e formas semelhantes em dimensões maiores). O ponto inicial e o ponto terminal do vetor estão nas extremidades opostas do retângulo (ou prisma, etc.).

Notação de conjunto ordenado

Um vetor retangular em pode ser especificado usando um conjunto ordenado de componentes, entre parênteses ou colchetes angulares. ${\ displaystyle \ mathbb {R} ^ {n}}$

Em um sentido geral, um vetor n- dimensional v pode ser especificado em uma das seguintes formas:

• ${\ displaystyle \ mathbf {v} = (v_ {1}, v_ {2}, \ dots, v_ {n-1}, v_ {n})}$
• ${\ displaystyle \ mathbf {v} = \ langle v_ {1}, v_ {2}, \ dots, v_ {n-1}, v_ {n} \ rangle}$

Onde v ₁ , v ₂ ,…, v _{n  - 1} , v _n são os componentes de v .

Notação de matriz

Um vetor retangular em também pode ser especificado como uma matriz de linha ou coluna contendo o conjunto ordenado de componentes. Um vetor especificado como matriz de linha é conhecido como vetor de linha ; aquele especificado como matriz de coluna é conhecido como vetor de coluna . ${\ displaystyle \ mathbb {R} ^ {n}}$

Novamente, um vetor n- dimensional pode ser especificado em qualquer uma das seguintes formas usando matrizes: ${\ displaystyle \ mathbf {v}}$

• ${\ displaystyle \ mathbf {v} = {\ begin {bmatrix} v_ {1} & v_ {2} & \ cdots & v_ {n-1} & v_ {n} \ end {bmatrix}} = {\ begin {pmatrix} v_ {1} & v_ {2} & \ cdots & v_ {n-1} & v_ {n} \ end {pmatrix}}}$
• ${\ displaystyle \ mathbf {v} = {\ begin {bmatrix} v_ {1} \\ v_ {2} \\\ vdots \\ v_ {n-1} \\ v_ {n} \ end {bmatrix}} = {\ begin {pmatrix} v_ {1} \\ v_ {2} \\\ vdots \\ v_ {n-1} \\ v_ {n} \ end {pmatrix}}}$

onde v ₁ , v ₂ ,…, v _{n  - 1} , v _n são os componentes de v . Em alguns contextos avançados, um vetor linha e coluna têm significados diferentes; veja covariância e contravariância de vetores para mais informações.

Notação de vetor de unidade

Um vetor retangular em (ou menos dimensões, como onde v _z abaixo é zero) pode ser especificado como a soma dos múltiplos escalares dos componentes do vetor com os membros da base padrão em . A base é representado com os vectores de unidade , e . ${\ displaystyle \ mathbb {R} ^ {3}}$${\ displaystyle \ mathbb {R} ^ {2}}$${\ displaystyle \ mathbb {R} ^ {3}}$ ${\ displaystyle {\ boldsymbol {\ hat {\ imath}}} = (1,0,0)}$${\ displaystyle {\ boldsymbol {\ hat {\ jmath}}} = (0,1,0)}$${\ displaystyle {\ boldsymbol {\ hat {k}}} = (0,0,1)}$

Um vetor tridimensional pode ser especificado da seguinte forma, usando a notação de vetor unitário: ${\ displaystyle {\ boldsymbol {v}}}$

• ${\ displaystyle \ mathbf {v} = v_ {x} {\ boldsymbol {\ hat {\ imath}}} + v_ {y} {\ boldsymbol {\ hat {\ jmath}}} + v_ {z} {\ boldsymbol {\ hat {k}}}}$

Onde v _x , v _y e v _z são os componentes escalares de v . Os componentes escalares podem ser positivos ou negativos; o valor absoluto de um componente escalar é sua magnitude.

Vetores polares

Os pontos no sistema de coordenadas polares com pólo S e polar eixo L . Em verde, o ponto com coordenada radial 3 e coordenada angular 60 graus, ou (3,60 °). Em azul, o ponto (4.210 °).

As duas coordenadas polares de um ponto em um plano podem ser consideradas como um vetor bidimensional. Esse vetor polar consiste em uma magnitude (ou comprimento) e uma direção (ou ângulo). A magnitude, normalmente representada como r , é a distância de um ponto de partida, a origem , até o ponto que é representado. O ângulo, normalmente representado como θ (a letra grega theta ), é o ângulo, geralmente medido no sentido anti-horário, entre uma direção fixa, normalmente a do eixo x positivo , e a direção da origem ao ponto. O ângulo é normalmente reduzido para ficar dentro da faixa de radianos ou . ${\ displaystyle 0 \ leq \ theta <2 \ pi}$${\ displaystyle 0 \ leq \ theta <360 ^ {\ circ}}$

Deve-se enfatizar que um vetor polar não é realmente um vetor , uma vez que a adição de dois vetores polares não é definida.

Conjunto ordenado e notações de matriz

Os vetores polares podem ser especificados usando notação de par ordenado (um subconjunto da notação de conjunto ordenado usando apenas dois componentes) ou notação de matriz, como acontece com vetores retangulares. Nessas formas, o primeiro componente do vetor é r (em vez de v ₁ ) e o segundo componente é θ (em vez de v ₂ ). Para diferenciar vetores polares de vetores retangulares, o ângulo pode ser prefixado com o símbolo de ângulo ,. ${\ displaystyle \ angle}$

Um vetor polar bidimensional v pode ser representado como qualquer um dos seguintes, usando par ordenado ou notação de matriz:

• ${\ displaystyle \ mathbf {v} = (r, \ angle \ theta)}$
• ${\ displaystyle \ mathbf {v} = \ langle r, \ angle \ theta \ rangle}$
• ${\ displaystyle \ mathbf {v} = {\ begin {bmatrix} r & \ angle \ theta \ end {bmatrix}}}$
• ${\ displaystyle \ mathbf {v} = {\ begin {bmatrix} r \\\ ângulo \ theta \ end {bmatrix}}}$

onde r é a magnitude, θ é o ângulo e o símbolo de ângulo ( ) é opcional. ${\ displaystyle \ angle}$

Notação direta

Os vetores polares também podem ser especificados usando equações autônomas simplificadas que definem r e θ explicitamente. Isso pode ser complicado, mas é útil para evitar a confusão com vetores retangulares bidimensionais que surgem do uso de par ordenado ou notação de matriz.

Um vetor bidimensional cuja magnitude é 5 unidades, e cuja direção é π / 9 radianos (20 °), pode ser especificado usando uma das seguintes formas:

• ${\ displaystyle r = 5, \ \ theta = {\ pi \ over 9}}$
• ${\ displaystyle r = 5, \ \ theta = 20 ^ {\ circ}}$

Vetores cilíndricos

Um sistema de coordenadas cilíndricas com origem ó , eixo polar A , e o eixo longitudinal L . O ponto é o ponto com distância radial ρ  = 4, coordenada angular φ  = 130 ° e altura z  = 4.

Um vetor cilíndrico é uma extensão do conceito de vetores polares em três dimensões. É semelhante a uma seta no sistema de coordenadas cilíndricas . Um vetor cilíndrico é especificado por uma distância no plano xy , um ângulo e uma distância do plano xy (uma altura). A primeira distância, geralmente representada como r ou ρ (a letra grega rho ), é a magnitude da projeção do vetor no plano xy . O ângulo, geralmente representado como θ ou φ (a letra grega phi ), é medido como o deslocamento da linha colinear com o eixo x na direção positiva; o ângulo é normalmente reduzido para ficar dentro do intervalo . A segunda distância, geralmente representada como h ou z , é a distância do plano xy ao ponto final do vetor. ${\ displaystyle 0 \ leq \ theta <2 \ pi}$

Conjunto ordenado e notações de matriz

Os vetores cilíndricos são especificados como vetores polares, onde o segundo componente de distância é concatenado como um terceiro componente para formar tripletos ordenados (novamente, um subconjunto de notação de conjunto ordenado) e matrizes. O ângulo pode ser prefixado com o símbolo do ângulo ( ); a combinação distância-ângulo-distância distingue vetores cilíndricos nesta notação de vetores esféricos em notação semelhante. ${\ displaystyle \ angle}$

Um vetor cilíndrico tridimensional v pode ser representado como qualquer um dos seguintes, usando tripleto ordenado ou notação de matriz:

• ${\ displaystyle \ mathbf {v} = (r, \ angle \ theta, h)}$
• ${\ displaystyle \ mathbf {v} = \ langle r, \ angle \ theta, h \ rangle}$
• ${\ displaystyle \ mathbf {v} = {\ begin {bmatrix} r & \ angle \ theta & h \ end {bmatrix}}}$
• ${\ displaystyle \ mathbf {v} = {\ begin {bmatriz} r \\\ ângulo \ theta \\ h \ end {bmatrix}}}$

Onde r é a magnitude da projeção de v no plano xy , θ é o ângulo entre o eixo x positivo ev , e h é a altura do plano xy até o ponto final de v . Novamente, o símbolo do ângulo ( ) é opcional. ${\ displaystyle \ angle}$

Notação direta

Um vetor cilíndrico também pode ser especificado diretamente, usando equações autônomas simplificadas que definem r (ou ρ ), θ (ou φ ) eh (ou z ). A consistência deve ser usada ao escolher os nomes a serem usados ​​para as variáveis; ρ não deve ser misturado com θ e assim por diante.

Um vetor tridimensional, cuja magnitude de projeção no plano xy é de 5 unidades, cujo ângulo do eixo x positivo é π / 9 radianos (20 °), e cuja altura do plano xy é de 3 unidades pode ser especificado em qualquer uma das seguintes formas:

• ${\ displaystyle r = 5, \ \ theta = {\ pi \ over 9}, \ h = 3}$
• ${\ displaystyle r = 5, \ \ theta = 20 ^ {\ circ}, \ h = 3}$
• ${\ displaystyle \ rho = 5, \ \ phi = {\ pi \ over 9}, \ z = 3}$
• ${\ displaystyle \ rho = 5, \ \ phi = 20 ^ {\ circ}, \ z = 3}$

Vetores esféricos

Coordenadas esféricas ( r , θ , φ ) frequentemente usadas em matemática : distância radial r , ângulo azimutal θ e ângulo polar φ . Os significados de θ e φ foram trocados em comparação com a convenção da física.

Um vetor esférico é outro método para estender o conceito de vetores polares em três dimensões. É semelhante a uma flecha no sistema de coordenadas esféricas . Um vetor esférico é especificado por uma magnitude, um ângulo de azimute e um ângulo de zênite. A magnitude geralmente é representada como ρ . O ângulo de azimute, geralmente representado como θ , é o deslocamento (sentido anti-horário) do eixo x positivo . O ângulo zenital, geralmente representado como φ , é o deslocamento do eixo z positivo . Ambos os ângulos são normalmente reduzidos para se situarem na faixa de zero (inclusivo) a 2 π (exclusivo).

Conjunto ordenado e notações de matriz

Os vetores esféricos são especificados como vetores polares, onde o ângulo zenital é concatenado como um terceiro componente para formar tripletos e matrizes ordenados. Os ângulos de azimute e zênite podem ser prefixados com o símbolo de ângulo ( ); o prefixo deve ser usado consistentemente para produzir a combinação distância-ângulo-ângulo que distingue os vetores esféricos dos cilíndricos. ${\ displaystyle \ angle}$

Um vetor esférico tridimensional v pode ser representado como qualquer um dos seguintes, usando tripleto ordenado ou notação de matriz:

• ${\ displaystyle \ mathbf {v} = (\ rho, \ angle \ theta, \ angle \ phi)}$
• ${\ displaystyle \ mathbf {v} = \ langle \ rho, \ angle \ theta, \ angle \ phi \ rangle}$
• ${\ displaystyle \ mathbf {v} = {\ begin {bmatrix} \ rho & \ angle \ theta & \ angle \ phi \ end {bmatrix}}}$
• ${\ displaystyle \ mathbf {v} = {\ begin {bmatriz} \ rho \\\ ângulo \ theta \\\ ângulo \ phi \ end {bmatriz}}}$

Onde ρ é a magnitude, θ é o ângulo do azimute e φ é o ângulo do zênite.

Notação direta

Como os vetores polares e cilíndricos, os vetores esféricos podem ser especificados usando equações autônomas simplificadas, neste caso para ρ , θ e φ .

Um vetor tridimensional cuja magnitude é 5 unidades, cujo ângulo de azimute é π / 9 radianos (20 °) e cujo ângulo zenital é π / 4 radianos (45 °) pode ser especificado como:

• ${\ displaystyle \ rho = 5, \ \ theta = {\ pi \ over 9}, \ \ phi = {\ pi \ over 4}}$
• ${\ displaystyle \ rho = 5, \ \ theta = 20 ^ {\ circ}, \ \ phi = 45 ^ {\ circ}}$

Operações

Em qualquer espaço vetorial dado , as operações de adição vetorial e multiplicação escalar são definidas. Espaços vetoriais normados também definem uma operação conhecida como norma (ou determinação de magnitude). Os espaços de produto interno também definem uma operação conhecida como produto interno. Em , o produto interno é conhecido como produto escalar . Em e , uma operação adicional conhecida como produto vetorial também é definida. ${\ displaystyle \ mathbb {R} ^ {n}}$${\ displaystyle \ mathbb {R} ^ {3}}$${\ displaystyle \ mathbb {R} ^ {7}}$

Adição de vetor

A adição de vetores é representada com o sinal de mais usado como um operador entre dois vetores. A soma de dois vetores u e v seria representado como:

${\ displaystyle \ mathbf {u} + \ mathbf {v}}$

Multiplicação escalar

A multiplicação escalar é representada da mesma maneira que a multiplicação algébrica. Um escalar ao lado de um vetor (um ou ambos podem estar entre parênteses) implica multiplicação escalar. Os dois operadores comuns, um ponto e uma cruz girada, também são aceitáveis ​​(embora a cruz girada quase nunca seja usada), mas eles correm o risco de confusão com produtos escalares e produtos cruzados, que operam em dois vetores. O produto de um escalar k com um vetor v pode ser representado em qualquer uma das seguintes formas:

• ${\ displaystyle k \ mathbf {v}}$
• ${\ displaystyle k \ cdot \ mathbf {v}}$

Subtração vetorial e divisão escalar

Usando as propriedades algébricas de subtração e divisão, junto com a multiplicação escalar, também é possível “subtrair” dois vetores e “dividir” um vetor por um escalar.

A subtração do vetor é realizada adicionando o múltiplo escalar de -1 com o segundo operando do vetor ao primeiro operando do vetor. Isso pode ser representado pelo uso do sinal de menos como um operador. A diferença entre os dois vectores de u e v pode ser representado em qualquer uma das seguintes formas:

• ${\ displaystyle \ mathbf {u} + - \ mathbf {v}}$
• ${\ displaystyle \ mathbf {u} - \ mathbf {v}}$

A divisão escalar é realizada multiplicando o operando vetorial pelo inverso numérico do operando escalar. Isso pode ser representado pelo uso da barra de fração ou sinais de divisão como operadores. O quociente de um vetor v e um escalar c pode ser representado em qualquer uma das seguintes formas:

• ${\ displaystyle {1 \ over c} \ mathbf {v}}$
• ${\ displaystyle {\ mathbf {v} \ over c}}$
• ${\ displaystyle {\ mathbf {v} \ div c}}$

Norma

A norma de um vetor é representada por barras duplas em ambos os lados do vetor. A norma de um vetor v pode ser representada como:

${\ displaystyle \ | \ mathbf {v} \ |}$

A norma também é às vezes representada com barras simples, como , mas isso pode ser confundido com valor absoluto (que é um tipo de norma). ${\ displaystyle | \ mathbf {v} |}$

Produto Interno

O produto interno de dois vetores (também conhecido como produto escalar, não deve ser confundido com multiplicação escalar) é representado como um par ordenado entre colchetes angulares. O produto interno de dois vectores de u e de v seria representado como:

${\ displaystyle \ langle \ mathbf {u}, \ mathbf {v} \ rangle}$

Produto interno

Em , o produto interno também é conhecido como produto escalar . Além da notação de produto interno padrão, a notação de produto escalar (usando o ponto como um operador) também pode ser usada (e é mais comum). O produto escalar de dois vetores u e v pode ser representado como: ${\ displaystyle \ mathbb {R} ^ {n}}$

${\ displaystyle \ mathbf {u} \ cdot \ mathbf {v}}$

Em alguma literatura mais antiga, o produto escalar está implícito entre dois vetores escritos lado a lado. Essa notação pode ser confundida com o produto diádico entre dois vetores.

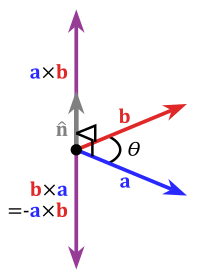
Produto cruzado

O produto vetorial de dois vetores (in ) é representado usando a cruz girada como um operador. O produto cruzado de dois vectores de u e de v seria representado como: ${\ displaystyle \ mathbb {R} ^ {3}}$

${\ displaystyle \ mathbf {u} \ times \ mathbf {v}}$

Por algumas convenções (por exemplo, na França e em algumas áreas da matemática superior), isso também é denotado por uma cunha, o que evita confusão com o produto da cunha, uma vez que os dois são funcionalmente equivalentes em três dimensões:

${\ displaystyle \ mathbf {u} \ wedge \ mathbf {v}}$

Em alguma literatura mais antiga, a seguinte notação é usada para o produto vetorial entre u e v :

${\ displaystyle [\ mathbf {u}, \ mathbf {v}]}$

Nabla

A notação vetorial é usada com cálculo por meio do operador Nabla :

${\ displaystyle \ mathbf {i} {\ frac {\ partial} {\ partial x}} + \ mathbf {j} {\ frac {\ partial} {\ partial y}} + \ mathbf {k} {\ frac { \ parcial} {\ parcial z}}}$

Com uma função escalar f , o gradiente é escrito como ${\ displaystyle \ nabla f \,}$

com um campo vetorial, F a divergência é escrita como ${\ displaystyle \ nabla \ cdot F,}$

e com um campo vetorial, F , o curl é escrito como ${\ displaystyle \ nabla \ times F.}$

Veja também

• Vetor euclidiano
• ISO 31-11 § Vetores e tensores
• Fasor

Referências