Grupo dicíclico - Dicyclic group

Estrutura algébrica → Teoria de grupos Teoria de grupos
Noções básicas Subgrupo Subgrupo normal Grupo de quociente Produto (semi) direto Homomorfismos de grupo núcleo imagem soma direta produto de grinalda simples finito infinito contínuo multiplicativo aditivo cíclico abeliano diédrico nilpotente solucionável açao Glossário da teoria dos grupos Lista de tópicos de teoria de grupo
Grupos finitos Classificação de grupos finitos simples cíclico alternando Tipo de mentira esporádico Teorema de Cauchy Teorema de Lagrange Teoremas de Sylow Teorema de Hall p-grupo Grupo abeliano elementar Grupo Frobenius Multiplicador Schur Grupo simétrico S n Klein quatro grupos V Grupo diédrico D n Quaternion grupo Q Grupo dicíclico Dic n
Grupos discretos Treliças Inteiros ( )${\ displaystyle \ mathbb {Z}}$ Grupo livre Grupos modulares PSL (2, )${\ displaystyle \ mathbb {Z}}$ SL (2, )${\ displaystyle \ mathbb {Z}}$ Grupo aritmético Malha Grupo hiperbólico
Grupos topológicos e de Lie Solenóide Círculo GL linear geral ( n ) SL linear especial ( n ) Ortogonal O ( n ) E Euclidiano ( n ) SO ortogonal especial ( n ) Unitária U ( n ) SU unitário especial ( n ) Sp simplético ( n ) G 2 F 4 E 6 E 7 E 8 Lorentz Poincaré Conforme Difeomorfismo Ciclo Grupo de Lie dimensional infinito O (∞) SU (∞) Sp (∞)
Grupos algébricos Grupo algébrico linear Grupo redutor Variedade abeliana Curva elíptica
v t e

Em teoria grupo , um grupo dicíclico (notação Dic _N ou Q _{4 n} , ⟨ n , 2,2⟩) é um tipo particular de grupo não-abeliano de ordem 4 n ( n > 1). É uma extensão do grupo cíclico de ordem 2 por um grupo cíclico de ordem 2 n , dando o nome de dicíclico . Na notação de sequências exatas de grupos, esta extensão pode ser expressa como:

${\ displaystyle 1 \ para C_ {2n} \ para {\ mbox {Dic}} _ {n} \ para C_ {2} \ para 1. \,}$

Mais geralmente, dado qualquer grupo abeliano finito com um elemento de ordem 2, pode-se definir um grupo dicíclico.

Definição

Para cada número inteiro n > 1, o grupo dicíclico Dic _n pode ser definido como o subgrupo dos quatérnios unitários gerados por

${\ displaystyle {\ begin {alinhados} a & = e ^ {\ frac {i \ pi} {n}} = \ cos {\ frac {\ pi} {n}} + i \ sin {\ frac {\ pi} {n}} \\ x & = j \ end {alinhado}}}$

Mais abstratamente, pode-se definir o grupo dicíclico Dic _n como o grupo com a seguinte apresentação

${\ displaystyle \ operatorname {Dic} _ {n} = \ left \ langle a, x \ mid a ^ {2n} = 1, \ x ^ {2} = a ^ {n}, \ x ^ {- 1} ax = a ^ {- 1} \ right \ rangle. \, \!}$

Algumas coisas a serem observadas que decorrem desta definição:

• ${\ displaystyle x ^ {4} = 1}$
• ${\ displaystyle x ^ {2} a ^ {k} = a ^ {k + n} = a ^ {k} x ^ {2}}$
• se então${\ displaystyle j = \ pm 1}$${\ displaystyle x ^ {j} a ^ {k} = a ^ {- k} x ^ {j}}$
• ${\ displaystyle a ^ {k} x ^ {- 1} = a ^ {kn} a ^ {n} x ^ {- 1} = a ^ {kn} x ^ {2} x ^ {- 1} = a ^ {kn} x}$

Assim, cada elemento de Dic _n pode ser escrito exclusivamente como um ^k x ^j , onde 0 ≤ k <2 n e j = 0 ou 1. As regras de multiplicação são dadas por

• ${\ displaystyle a ^ {k} a ^ {m} = a ^ {k + m}}$
• ${\ displaystyle a ^ {k} a ^ {m} x = a ^ {k + m} x}$
• ${\ displaystyle a ^ {k} xa ^ {m} = a ^ {km} x}$
• ${\ displaystyle a ^ {k} xa ^ {m} x = a ^ {k-m + n}}$

Conclui-se que Dic _n tem ordem 4 n .

Quando n = 2, o grupo dicíclico é isomorfo para o grupo Quatérnion Q . Mais geralmente, quando n é uma potência de 2, o grupo dicíclico é isomórfico ao grupo quatérnio generalizado .

Propriedades

Para cada n > 1, o grupo dicíclico Dic _n é um grupo não abeliano de ordem 4 n . (Para o caso degenerado n = 1, o grupo Dic ₁ é o grupo cíclico C ₄ , que não é considerado dicíclico.)

Deixe Um = ⟨ um ⟩ ser o subgrupo de Dic _n gerado por um . Então A é um grupo cíclico de ordem 2 n , então [Dic _n : A ] = 2. Como um subgrupo do índice 2, é automaticamente um subgrupo normal . O grupo quociente Dic _n / A é um grupo cíclico de ordem 2.

Dic _n tem solução ; observe que A é normal e, sendo abeliano, pode ser resolvido.

Grupo diédrico binário

O grupo dicíclico é um grupo poliédrico binário - é uma das classes de subgrupos do grupo Pin Pin _- (2), que é um subgrupo do grupo Spin Spin (3) - e neste contexto é conhecido como o diédrico binário grupo .

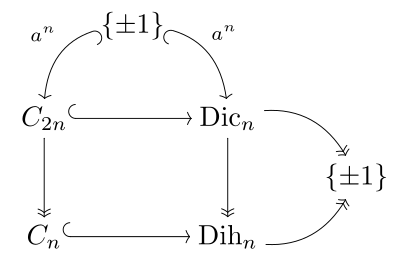
A conexão com o grupo cíclico binário C _{2 n} , o grupo cíclico C _n e o grupo diédrico Dih _n de ordem 2 n é ilustrada no diagrama à direita e é paralela ao diagrama correspondente para o grupo de pinos. Coxeter escreve o grupo diedro binário como ⟨2,2, n ⟩ e grupo cíclico binário com cantoneiras de suportes, ⟨ n ⟩.

Existe uma semelhança superficial entre os grupos dicíclicos e os grupos diédricos ; ambos são uma espécie de "espelhamento" de um grupo cíclico subjacente. Mas a apresentação de um grupo diedro teria x ² = 1, em vez de x ² = a ⁿ ; e isso produz uma estrutura diferente. Em particular, Dic _n não é um produto semidirect de A e ⟨ x ⟩, desde Um  ∩ ⟨ x ⟩ não é trivial.

O grupo dicíclico tem uma involução única (ou seja, um elemento de ordem 2), a saber, x ² = a ⁿ . Observe que esse elemento está no centro de Dic _n . De fato, o centro consiste unicamente do elemento de identidade e x ² . Se adicionarmos a relação x ² = 1 à apresentação de Dic _n, obtém-se uma apresentação do grupo diédrico Dih _n , de modo que o grupo quociente Dic _n / < x ² > é isomorfo a Dih _n .

Há um homomorfismo 2 para 1 natural do grupo de quatérnios unitários para o grupo de rotação tridimensional descrito em quatérnios e rotações espaciais . Uma vez que o grupo dicíclico pode estar embutido dentro dos quatérnios unitários, pode-se perguntar qual é a imagem dele sob esse homomorfismo. A resposta é apenas o grupo de simetria diédrica Dih _n . Por esta razão, o grupo dicíclico também é conhecido como grupo diédrico binário . Observe que o grupo dicíclico não contém nenhum subgrupo isomórfico a Dih _n .

A construção de pré-imagem análoga, usando Pin ₊ (2) em vez de Pin _- (2), produz outro grupo diédrico, Dih _{2 n} , em vez de um grupo dicíclico.

Generalizações

Seja A um grupo abeliano , tendo um elemento específico y em A com ordem 2. Um grupo G é chamado de grupo dicíclico generalizado , escrito como Dic ( A , y ) , se for gerado por A e um elemento adicional x , e além disso, temos que [ G : A ] = 2, x ² = y , e para todo a em A , x ⁻¹ ax = a ⁻¹ .

Visto que para um grupo cíclico de ordem par, há sempre um elemento único de ordem 2, podemos ver que os grupos dicíclicos são apenas um tipo específico de grupo dicíclico generalizado.

Veja também

• grupo poliédrico binário
• grupo cíclico binário , ⟨ n ⟩, ordem 2 n
• grupo tetraédrico binário , 2T = ⟨2,3,3⟩, ordem 24
• grupo octaédrico binário , 2O = ⟨2,3,4⟩, ordem 48
• grupo icosaédrico binário , 2I = ⟨2,3,5⟩, ordem 120

Referências

links externos

• Grupos dicíclicos em GroupNames