Análise fatorial - Factor analysis
A análise fatorial é um método estatístico usado para descrever a variabilidade entre as variáveis observadas e correlacionadas em termos de um número potencialmente menor de variáveis não observadas chamadas de fatores . Por exemplo, é possível que variações em seis variáveis observadas reflitam principalmente as variações em duas variáveis não observadas (subjacentes). A análise fatorial procura por tais variações conjuntas em resposta a variáveis latentes não observadas . As variáveis observadas são modeladas como combinações lineares dos fatores potenciais, mais os termos de " erro ".
Simplificando, a carga fatorial de uma variável quantifica até que ponto a variável está relacionada com um determinado fator.
Um raciocínio comum por trás dos métodos analíticos de fator é que as informações obtidas sobre as interdependências entre as variáveis observadas podem ser usadas posteriormente para reduzir o conjunto de variáveis em um conjunto de dados. A análise fatorial é comumente usada em psicometria , teorias da personalidade , biologia, marketing , gerenciamento de produto , pesquisa operacional , finanças e aprendizado de máquina . Pode ajudar a lidar com conjuntos de dados onde há um grande número de variáveis observadas que se pensa refletem um número menor de variáveis latentes / subjacentes. É uma das técnicas de interdependência mais comumente usadas e é usada quando o conjunto relevante de variáveis mostra uma interdependência sistemática e o objetivo é descobrir os fatores latentes que criam uma comunalidade.
Modelo estatístico
Definição
O modelo tenta explicar um conjunto de observações em cada um dos indivíduos com um conjunto de fatores comuns ( ) onde há menos fatores por unidade do que observações por unidade ( ). Cada indivíduo possui seus próprios fatores comuns, e estes estão relacionados às observações via matriz de carga fatorial ( ), para uma única observação, de acordo com
através do qual
- é o valor da ª observação do ª indivíduo,
- é a média de observação para a ª observação,
- é o carregamento para a ésima observação do ésimo fator,
- é o valor do ésimo fator do ésimo indivíduo, e
- é o º termo de erro estocástico não observado com média zero e variância finita.
Em notação matricial
onde matriz de observação , matriz de fator, matriz de termo de erro e matriz de média em que o ésimo elemento é simplesmente .
Além disso, imporemos as seguintes suposições sobre :
- e são independentes.
- ; onde está a expectativa
- onde está a matriz de covariância , para se certificar de que os fatores não estão correlacionados, e é a matriz de identidade .
Suponha . Então
e, portanto, a partir das condições impostas acima,
ou, configuração ,
Observe que, para qualquer matriz ortogonal , se definirmos e , os critérios para serem fatores e cargas fatoriais ainda serão válidos. Portanto, um conjunto de fatores e cargas fatoriais é único até uma transformação ortogonal .
Exemplo
Suponha que um psicólogo tenha a hipótese de que existem dois tipos de inteligência , "inteligência verbal" e "inteligência matemática", nenhuma das quais é diretamente observada. A evidência para a hipótese é buscada nas notas dos exames de cada um dos 10 campos acadêmicos diferentes de 1000 alunos. Se cada aluno for escolhido aleatoriamente em uma grande população , as 10 pontuações de cada aluno serão variáveis aleatórias. A hipótese do psicólogo pode dizer que para cada um dos 10 campos acadêmicos, a pontuação média sobre o grupo de todos os alunos que compartilham algum par comum de valores para "inteligências" verbais e matemáticas é alguma constante vezes seu nível de inteligência verbal mais outra constante seu nível de inteligência matemática, ou seja, é uma combinação linear desses dois "fatores". Os números para um determinado assunto, pelos quais os dois tipos de inteligência são multiplicados para obter a pontuação esperada, são postulados pela hipótese de serem os mesmos para todos os pares de nível de inteligência e são chamados de "carga fatorial" para este assunto. Por exemplo, a hipótese pode sustentar que a aptidão do aluno médio previsto no campo da astronomia é
- {10 × a inteligência verbal do aluno} + {6 × a inteligência matemática do aluno}.
Os números 10 e 6 são as cargas fatoriais associadas à astronomia. Outras disciplinas acadêmicas podem ter diferentes cargas fatoriais.
Dois alunos assumidos como tendo graus idênticos de inteligência verbal e matemática podem ter aptidões medidas diferentes em astronomia porque as aptidões individuais diferem das aptidões médias (preditas acima) e por causa do próprio erro de medida. Essas diferenças constituem o que é chamado coletivamente de "erro" - um termo estatístico que significa a quantidade pela qual um indivíduo, conforme medido, difere do que é médio ou previsto por seus níveis de inteligência (ver erros e resíduos nas estatísticas )
Os dados observáveis que entram na análise fatorial seriam 10 pontuações de cada um dos 1.000 alunos, um total de 10.000 números. As cargas fatoriais e os níveis dos dois tipos de inteligência de cada aluno devem ser inferidos dos dados.
Modelo matemático do mesmo exemplo
A seguir, as matrizes serão indicadas por variáveis indexadas. Os índices de "assunto" serão indicados por letras , e , com valores que vão de até que é igual a no exemplo acima. Índices de "fator" serão indicados por letras , e , com valores que vão de a que é igual a no exemplo acima. Os índices de "instância" ou "amostra" serão indicados por letras , e , com valores variando de a . No exemplo acima, se uma amostra de alunos participou dos exames, a nota do aluno para o º exame é dada por . O objetivo da análise fatorial é caracterizar as correlações entre as variáveis das quais são uma instância particular, ou conjunto de observações. Para que as variáveis estejam em pé de igualdade, elas são normalizadas em pontuações padrão :
onde a média da amostra é:
e a variação da amostra é dada por:
O modelo de análise fatorial para esta amostra em particular é então:
ou, mais sucintamente:
Onde
- é a "inteligência verbal" do aluno,
- é a "inteligência matemática" do aluno,
- são as cargas fatoriais para o º assunto, para .
Em notação de matriz , temos
Observe que dobrar a escala em que a "inteligência verbal" - o primeiro componente em cada coluna de - é medida e, simultaneamente, reduzir pela metade as cargas fatoriais da inteligência verbal não faz diferença para o modelo. Assim, nenhuma generalidade é perdida assumindo que o desvio padrão dos fatores para a inteligência verbal é . Da mesma forma para a inteligência matemática. Além disso, por razões semelhantes, nenhuma generalidade é perdida assumindo que os dois fatores não estão correlacionados um com o outro. Em outras palavras:
onde é o delta de Kronecker ( quando e quando ). Os erros são considerados independentes dos fatores:
Observe que, como qualquer rotação de uma solução também é uma solução, isso dificulta a interpretação dos fatores. Veja as desvantagens abaixo. Neste exemplo particular, se não sabemos de antemão que os dois tipos de inteligência não estão correlacionados, então não podemos interpretar os dois fatores como os dois tipos diferentes de inteligência. Mesmo se eles não estiverem correlacionados, não podemos dizer qual fator corresponde à inteligência verbal e qual corresponde à inteligência matemática sem um argumento externo.
Os valores dos carregamentos , as médias e as variâncias dos "erros" devem ser estimados dados os dados observados e (a suposição sobre os níveis dos fatores é fixa para um dado ). O "teorema fundamental" pode ser derivado das condições acima:
O termo à esquerda é o -termo da matriz de correlação (uma matriz derivada como o produto da matriz de observações padronizadas com sua transposição) dos dados observados, e seus elementos diagonais serão s. O segundo termo à direita será uma matriz diagonal com termos menores que a unidade. O primeiro termo à direita é a "matriz de correlação reduzida" e será igual à matriz de correlação, exceto por seus valores diagonais, que serão menores que a unidade. Esses elementos diagonais da matriz de correlação reduzida são chamados de "comunalidades" (que representam a fração da variância na variável observada que é contabilizada pelos fatores):
É claro que os dados da amostra não obedecerão exatamente à equação fundamental dada acima devido a erros de amostragem, inadequação do modelo, etc. O objetivo de qualquer análise do modelo acima é encontrar os fatores e cargas que, em algum sentido, dar um "melhor ajuste" aos dados. Na análise fatorial, o melhor ajuste é definido como o mínimo do erro quadrático médio nos resíduos fora da diagonal da matriz de correlação:
Isso é equivalente a minimizar os componentes fora da diagonal da covariância do erro que, nas equações do modelo, têm valores esperados de zero. Isso deve ser contrastado com a análise de componentes principais, que busca minimizar o erro quadrático médio de todos os resíduos. Antes do advento dos computadores de alta velocidade, um esforço considerável foi dedicado a encontrar soluções aproximadas para o problema, particularmente na estimativa das comunalidades por outros meios, o que então simplifica o problema consideravelmente, produzindo uma matriz de correlação reduzida conhecida. Isso foi então usado para estimar os fatores e as cargas. Com o advento dos computadores de alta velocidade, o problema de minimização pode ser resolvido iterativamente com velocidade adequada, e as comunalidades são calculadas no processo, ao invés de serem necessárias de antemão. O algoritmo MinRes é particularmente adequado para esse problema, mas dificilmente é o único meio iterativo de encontrar uma solução.
Se os fatores de solução podem ser correlacionados (como na rotação 'oblimin', por exemplo), então o modelo matemático correspondente usa coordenadas oblíquas em vez de coordenadas ortogonais.
Interpretação geométrica
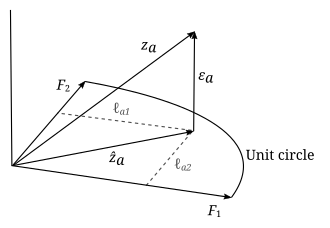
Os parâmetros e variáveis da análise fatorial podem receber uma interpretação geométrica. Os dados ( ), os fatores ( ) e os erros ( ) podem ser vistos como vetores em um espaço euclidiano dimensional (espaço amostral), representados como , e respectivamente. Como os dados são padronizados, os vetores de dados têm comprimento unitário ( ). Os vetores de fator definem um subespaço linear dimensional (ou seja, um hiperplano) neste espaço, sobre o qual os vetores de dados são projetados ortogonalmente. Isso segue da equação do modelo
ea independência dos fatores e os erros: . No exemplo acima, o hiperplano é apenas um plano bidimensional definido pelos dois vetores de fator. A projeção dos vetores de dados no hiperplano é dada por
e os erros são vetores desse ponto projetado até o ponto de dados e são perpendiculares ao hiperplano. O objetivo da análise fatorial é encontrar um hiperplano que seja um "melhor ajuste" aos dados em algum sentido, então não importa como os vetores de fator que definem este hiperplano são escolhidos, desde que sejam independentes e estejam em o hiperplano. Somos livres para especificá-los como ortogonais e normais ( ) sem perda de generalidade. Depois que um conjunto adequado de fatores é encontrado, eles também podem ser rotacionados arbitrariamente dentro do hiperplano, de modo que qualquer rotação dos vetores de fator defina o mesmo hiperplano e também seja uma solução. Como resultado, no exemplo acima, no qual o hiperplano de ajuste é bidimensional, se não sabemos de antemão que os dois tipos de inteligência não estão correlacionados, então não podemos interpretar os dois fatores como os dois tipos diferentes de inteligência. Mesmo se eles não estiverem correlacionados, não podemos dizer qual fator corresponde à inteligência verbal e qual corresponde à inteligência matemática, ou se os fatores são combinações lineares de ambos, sem um argumento externo.
Os vetores de dados têm comprimento unitário. As entradas da matriz de correlação para os dados são fornecidas por . A matriz de correlação pode ser interpretada geometricamente como o cosseno do ângulo entre os dois vetores de dados e . Os elementos diagonais serão claramente se os elementos fora da diagonal terão valores absolutos menores ou iguais à unidade. A "matriz de correlação reduzida" é definida como
- .
O objetivo da análise fatorial é escolher o hiperplano de ajuste de forma que a matriz de correlação reduzida reproduza a matriz de correlação o mais próximo possível, exceto para os elementos diagonais da matriz de correlação que são conhecidos por terem valor unitário. Em outras palavras, o objetivo é reproduzir com a maior precisão possível as correlações cruzadas nos dados. Especificamente, para o hiperplano de ajuste, o erro quadrático médio nos componentes fora da diagonal
deve ser minimizado, e isso é realizado minimizando-o em relação a um conjunto de vetores de fatores ortonormais. Pode ser visto que
O termo à direita é apenas a covariância dos erros. No modelo, a covariância do erro é declarada como uma matriz diagonal e, portanto, o problema de minimização acima irá de fato produzir um "melhor ajuste" para o modelo: Ele renderá uma estimativa da amostra da covariância do erro que tem seus componentes fora da diagonal minimizado no sentido do quadrado médio. Pode-se ver que, uma vez que são projeções ortogonais dos vetores de dados, seu comprimento será menor ou igual ao comprimento do vetor de dados projetado, que é a unidade. O quadrado desses comprimentos são apenas os elementos diagonais da matriz de correlação reduzida. Esses elementos diagonais da matriz de correlação reduzida são conhecidos como "comunalidades":
Grandes valores das comunalidades indicarão que o hiperplano de ajuste está reproduzindo com bastante precisão a matriz de correlação. Os valores médios dos fatores também devem ser restritos a zero, de onde se segue que os valores médios dos erros também serão zero.
Implementação prática
Tipos de análise fatorial
Análise fatorial exploratória
A análise fatorial exploratória (AFE) é usada para identificar inter-relações complexas entre itens e itens de grupo que fazem parte de conceitos unificados. O pesquisador não faz suposições a priori sobre as relações entre os fatores.
Análise fatorial confirmatória
A análise fatorial confirmatória (CFA) é uma abordagem mais complexa que testa a hipótese de que os itens estão associados a fatores específicos. O CFA usa modelagem de equações estruturais para testar um modelo de medição em que o carregamento nos fatores permite a avaliação das relações entre as variáveis observadas e as não observadas. As abordagens de modelagem de equação estrutural podem acomodar erros de medição e são menos restritivas do que a estimativa de mínimos quadrados . Modelos hipotetizados são testados contra dados reais, e a análise demonstraria carregamentos de variáveis observadas nas variáveis latentes (fatores), bem como a correlação entre as variáveis latentes.
Tipos de extração de fator
A análise de componentes principais (PCA) é um método amplamente utilizado para extração de fator, que é a primeira fase da EFA. As ponderações dos fatores são calculadas para extrair a variância máxima possível, com a continuação da fatoração sucessiva até que não haja mais nenhuma variância significativa restante. O modelo de fator deve então ser rotacionado para análise.
A análise fatorial canônica, também chamada de fatoração canônica de Rao, é um método diferente de calcular o mesmo modelo do PCA, que usa o método do eixo principal. A análise fatorial canônica busca os fatores que apresentam a maior correlação canônica com as variáveis observadas. A análise fatorial canônica não é afetada pelo redimensionamento arbitrário dos dados.
A análise de fator comum, também chamada de análise de fator principal (PFA) ou fatoração de eixo principal (PAF), busca o mínimo de fatores que podem explicar a variância comum (correlação) de um conjunto de variáveis.
A fatoração de imagens é baseada na matriz de correlação de variáveis preditas em vez de variáveis reais, onde cada variável é predita a partir das outras usando regressão múltipla .
A fatoração alfa é baseada na maximização da confiabilidade dos fatores, assumindo que as variáveis são amostradas aleatoriamente a partir de um universo de variáveis. Todos os outros métodos pressupõem que os casos sejam amostrados e as variáveis fixadas.
O modelo de regressão de fator é um modelo combinatório de modelo de fator e modelo de regressão; ou, alternativamente, pode ser visto como o modelo de fator híbrido, cujos fatores são parcialmente conhecidos.
Terminologia
Cargas de fator: Comunalidade é o quadrado da carga externa padronizada de um item. Análogo ao r- quadrado de Pearson , a carga fatorial quadrada é a porcentagem da variância nessa variável indicadora explicada pelo fator. Para obter a porcentagem de variância em todas as variáveis contabilizadas por cada fator, some a soma das cargas fatoriais quadradas para aquele fator (coluna) e divida pelo número de variáveis. (Observe que o número de variáveis é igual à soma de suas variâncias, pois a variância de uma variável padronizada é 1.) Isso é o mesmo que dividir o autovalor do fator pelo número de variáveis.
Interpretando as cargas fatoriais: Por uma regra prática na análise fatorial confirmatória, as cargas devem ser de 0,7 ou mais para confirmar que as variáveis independentes identificadas a priori são representadas por um fator particular, com base na lógica de que o nível .7 corresponde a cerca de metade do variação no indicador sendo explicada pelo fator. No entanto, o padrão .7 é alto e os dados da vida real podem muito bem não atender a esse critério, razão pela qual alguns pesquisadores, especialmente para fins exploratórios, usarão um nível inferior, como .4 para o fator central e .25 para outros fatores. Em qualquer caso, as cargas fatoriais devem ser interpretadas à luz da teoria, não por níveis de corte arbitrários.
Na rotação oblíqua , pode-se examinar uma matriz de padrão e uma matriz de estrutura. A matriz de estrutura é simplesmente a matriz de carga fatorial como na rotação ortogonal, representando a variância em uma variável medida explicada por um fator em uma base de contribuições única e comum. A matriz padrão, em contraste, contém coeficientes que representam apenas contribuições únicas. Quanto mais fatores, mais baixos os coeficientes de padrão via de regra, pois haverá mais contribuições comuns para a explicação da variância. Para rotação oblíqua, o pesquisador olha para os coeficientes de estrutura e padrão ao atribuir um rótulo a um fator. Os princípios da rotação oblíqua podem ser derivados tanto da entropia cruzada quanto de sua entropia dupla.
Comunalidade: A soma das cargas fatoriais quadradas para todos os fatores para uma determinada variável (linha) é a variância nessa variável contabilizada por todos os fatores. A comunalidade mede o percentual de variância em uma determinada variável explicada por todos os fatores em conjunto e pode ser interpretada como a confiabilidade do indicador no contexto dos fatores sendo postulados.
Soluções espúrias: Se a comunalidade exceder 1,0, há uma solução espúria, que pode refletir uma amostra muito pequena ou a escolha de extrair muitos ou poucos fatores.
Singularidade de uma variável: A variabilidade de uma variável menos sua comunalidade.
Valores próprios / raízes características: os valores próprios medem a quantidade de variação na amostra total considerada por cada fator. A proporção dos autovalores é a proporção da importância explicativa dos fatores em relação às variáveis. Se um fator tem um autovalor baixo, então ele contribui pouco para a explicação das variâncias nas variáveis e pode ser ignorado como menos importante do que os fatores com autovalores mais altos.
Extração de somas de cargas quadradas: autovalores iniciais e autovalores após a extração (listados pelo SPSS como "Extraction Sums of Squared Loadings") são as mesmas para extração de PCA, mas para outros métodos de extração, autovalores após a extração serão menores do que suas contrapartes iniciais. O SPSS também imprime "Soma de Rotação de Cargas Quadradas" e mesmo para PCA, esses autovalores serão diferentes dos autovalores iniciais e de extração, embora seu total seja o mesmo.
Pontuações de fator (também chamadas de pontuações de componentes no PCA): são as pontuações de cada caso (linha) em cada fator (coluna). Para calcular a pontuação do fator para um determinado caso para um determinado fator, toma-se a pontuação padronizada do caso em cada variável, multiplica-se pelos carregamentos correspondentes da variável para o fator dado e soma esses produtos. O cálculo das pontuações dos fatores permite que se busquem outliers do fator. Além disso, as pontuações dos fatores podem ser usadas como variáveis na modelagem subsequente. (Explicado do PCA, não da perspectiva da Análise Fatorial).
Critérios para determinar o número de fatores
Os pesquisadores desejam evitar critérios subjetivos ou arbitrários para retenção de fator, pois "fazia sentido para mim". Vários métodos objetivos foram desenvolvidos para resolver esse problema, permitindo aos usuários determinar uma gama apropriada de soluções a serem investigadas. Os métodos podem não concordar. Por exemplo, a análise paralela pode sugerir 5 fatores enquanto o MAP de Velicer sugere 6, então o pesquisador pode solicitar soluções de 5 e 6 fatores e discutir cada uma em termos de sua relação com dados externos e teoria.
Critérios modernos
Análise paralela de Horn (PA): Um método de simulação baseado em Monte-Carlo que compara os autovalores observados com aqueles obtidos a partir de variáveis normais não correlacionadas. Um fator ou componente é retido se o autovalor associado for maior do que o percentil 95 da distribuição de autovalores derivados dos dados aleatórios. PA está entre as regras mais comumente recomendadas para determinar o número de componentes a serem retidos, mas muitos programas falham em incluir essa opção (uma exceção notável é R ). No entanto, Formann forneceu evidências teóricas e empíricas de que sua aplicação pode não ser apropriada em muitos casos, uma vez que seu desempenho é consideravelmente influenciado pelo tamanho da amostra , discriminação de itens e tipo de coeficiente de correlação .
O teste MAP de Velicer (1976), conforme descrito por Courtney (2013) “envolve uma análise completa dos componentes principais seguida pelo exame de uma série de matrizes de correlações parciais” (p. 397 (embora note que esta citação não ocorre em Velicer (1976) ) e o número da página citada está fora das páginas da citação). A correlação quadrada para a Etapa "0" (consulte a Figura 4) é a correlação quadrática média fora da diagonal para a matriz de correlação não parcial. Na Etapa 1, o primeiro componente principal e seus itens associados são parcializados. Depois disso, a correlação quadrada média fora da diagonal para a matriz de correlação subsequente é então calculada para a Etapa 1. Na Etapa 2, os dois primeiros componentes principais são parcialmente eliminados e a correlação quadrática média resultante fora da diagonal é calculado novamente. Os cálculos são realizados para k menos uma etapa (k representando o número total de variáveis na matriz). Depois disso, todas as correlações quadradas médias para cada etapa são li ned up e o número da etapa nas análises que resultaram na menor correlação parcial quadrada média determinam o número de componentes ou fatores a reter. Por este método, os componentes são mantidos desde que a variância na matriz de correlação represente a variância sistemática, em oposição à variância residual ou de erro. Embora metodologicamente semelhante à análise de componentes principais, a técnica de MAP demonstrou um bom desempenho na determinação do número de fatores a serem retidos em estudos de simulação múltipla. Este procedimento é disponibilizado através de interface de usuário do SPSS, bem como o psych pacote para o idioma R programação .
Métodos mais antigos
Critério de Kaiser: a regra de Kaiser é eliminar todos os componentes com autovalores abaixo de 1,0 - sendo este o autovalor igual à informação contabilizada por um único item médio. O critério de Kaiser é o padrão no SPSS e na maioria dos softwares estatísticos, mas não é recomendado quando usado como o único critério de corte para estimar o número de fatores, pois tende a superextrá-los. Uma variação desse método foi criada onde um pesquisador calcula intervalos de confiança para cada autovalor e retém apenas os fatores que têm o intervalo de confiança inteiro maior que 1,0.
Cascalho trama : A Cattell cascalho parcelas de teste os componentes que o eixo dos X e os correspondentes valores eigen como o eixo Y . À medida que se move para a direita, em direção aos componentes posteriores, os valores próprios caem. Quando a queda cessa e a curva faz uma curva em direção a um declínio menos acentuado, o teste de degrau de Cattell diz para largar todos os outros componentes após aquele que começa no cotovelo. Esta regra é às vezes criticada por ser passível de " falsificação " controlada pelo pesquisador . Ou seja, como escolher o "cotovelo" pode ser subjetivo porque a curva tem vários cotovelos ou é uma curva suave, o pesquisador pode ser tentado a definir o ponto de corte no número de fatores desejados por sua agenda de pesquisa.
Critérios de explicação da variação: Alguns pesquisadores simplesmente usam a regra de manter fatores suficientes para responder por 90% (às vezes 80%) da variação. Onde o objetivo do pesquisador enfatiza a parcimônia (explicando a variância com o mínimo de fatores possível), o critério pode ser tão baixo quanto 50%.
Método bayesiano
Uma abordagem bayesiana baseada no processo de buffet indiano retorna uma distribuição de probabilidade sobre o número plausível de fatores latentes.
Métodos de rotação
A saída não girada maximiza a variância explicada pelo primeiro fator e pelos fatores subsequentes e força os fatores a serem ortogonais . Essa compactação de dados tem o custo de ter a maioria dos itens carregados nos fatores iniciais e, geralmente, de ter muitos itens carregados substancialmente em mais de um fator. A rotação serve para tornar a saída mais compreensível, buscando a chamada "Estrutura Simples": Um padrão de carregamentos onde cada item carrega fortemente em apenas um dos fatores, e muito mais fracamente nos outros fatores. As rotações podem ser ortogonais ou oblíquas (permitindo que os fatores se correlacionem).
A rotação Varimax é uma rotação ortogonal dos eixos do fator para maximizar a variância das cargas quadradas de um fator (coluna) em todas as variáveis (linhas) em uma matriz de fator, que tem o efeito de diferenciar as variáveis originais pelo fator extraído. Cada fator tenderá a ter cargas grandes ou pequenas de qualquer variável particular. Uma solução varimax produz resultados que tornam tão fácil quanto possível identificar cada variável com um único fator. Esta é a opção de rotação mais comum. No entanto, a ortogonalidade (ou seja, independência) dos fatores é frequentemente uma suposição irreal. As rotações oblíquas incluem a rotação ortogonal e, por esse motivo, as rotações oblíquas são o método preferido. Permitir fatores que estão correlacionados entre si é especialmente aplicável na pesquisa psicométrica, uma vez que atitudes, opiniões e habilidades intelectuais tendem a estar correlacionadas, e uma vez que seria irreal em muitas situações assumir o contrário.
A rotação de quartimax é uma alternativa ortogonal que minimiza o número de fatores necessários para explicar cada variável. Esse tipo de rotação geralmente gera um fator geral no qual a maioria das variáveis são carregadas em um grau alto ou médio. Essa estrutura de fatores geralmente não é útil para o propósito da pesquisa.
A rotação Equimax é um meio-termo entre os critérios varimax e quartimax.
A rotação oblimina direta é o método padrão quando se deseja uma solução não ortogonal (oblíqua) - isto é, aquela em que os fatores podem ser correlacionados. Isso resultará em autovalores mais elevados, mas diminuiu a interpretabilidade dos fatores. Veja abaixo.
A rotação Promax é um método alternativo de rotação não ortogonal (oblíqua) que é computacionalmente mais rápido do que o método oblimin direto e, portanto, às vezes é usado para conjuntos de dados muito grandes .
Análise de fator de ordem superior
A análise fatorial de ordem superior é um método estatístico que consiste em repetir a análise fatorial de etapas - rotação oblíqua - análise fatorial de fatores rotacionados. Seu mérito é permitir ao pesquisador perceber a estrutura hierárquica dos fenômenos estudados. Para interpretar os resultados, procede-se pela pós-multiplicação da matriz de padrão de fator primário pelas matrizes de padrão de fator de ordem superior (Gorsuch, 1983) e talvez aplicando uma rotação Varimax ao resultado (Thompson, 1990) ou usando um Schmid- Solução de Leiman (SLS, Schmid & Leiman, 1957, também conhecida como transformação de Schmid-Leiman) que atribui a variação dos fatores primários aos fatores de segunda ordem.
Em psicometria
História
Charles Spearman foi o primeiro psicólogo a discutir a análise de fator comum e o fez em seu artigo de 1904. Fornecia poucos detalhes sobre seus métodos e preocupava-se com modelos de fator único. Ele descobriu que as pontuações das crianças em idade escolar em uma ampla variedade de assuntos aparentemente não relacionados estavam positivamente correlacionadas, o que o levou a postular que uma única habilidade mental geral, ou g , fundamenta e molda o desempenho cognitivo humano.
O desenvolvimento inicial da análise de fator comum com múltiplos fatores foi dado por Louis Thurstone em dois artigos no início dos anos 1930, resumidos em seu livro de 1935, The Vector of Mind . Thurstone introduziu vários conceitos importantes de análise de fator, incluindo comunalidade, exclusividade e rotação. Ele defendeu uma "estrutura simples", e desenvolveu métodos de rotação que poderiam ser usados como forma de conseguir tal estrutura.
Na metodologia Q , Stephenson, um aluno de Spearman, distingue entre a análise do fator R , orientada para o estudo das diferenças interindividuais, e a análise do fator Q orientada para as diferenças subjetivas intra-individuais.
Raymond Cattell foi um forte defensor da análise fatorial e da psicometria e usou a teoria multifatorial de Thurstone para explicar a inteligência. Cattell também desenvolveu o teste "scree" e coeficientes de similaridade.
Aplicações em psicologia
A análise fatorial é usada para identificar "fatores" que explicam uma variedade de resultados em diferentes testes. Por exemplo, a pesquisa de inteligência descobriu que as pessoas que obtêm uma pontuação alta em um teste de habilidade verbal também são boas em outros testes que exigem habilidades verbais. Os pesquisadores explicaram isso usando a análise fatorial para isolar um fator, geralmente chamado de inteligência verbal, que representa o grau em que alguém é capaz de resolver problemas envolvendo habilidades verbais.
A análise fatorial em psicologia é mais frequentemente associada à pesquisa de inteligência. No entanto, também tem sido usado para encontrar fatores em uma ampla gama de domínios, como personalidade, atitudes, crenças, etc. Está ligado à psicometria , pois pode avaliar a validade de um instrumento ao descobrir se o instrumento realmente mede o postulado fatores.
A análise fatorial é uma técnica frequentemente usada em pesquisas interculturais. Ele serve ao propósito de extrair dimensões culturais . Os modelos de dimensões culturais mais conhecidos são os elaborados por Geert Hofstede , Ronald Inglehart , Christian Welzel , Shalom Schwartz e Michael Minkov.
Vantagens
- Redução do número de variáveis, combinando duas ou mais variáveis em um único fator. Por exemplo, desempenho em corrida, lançamento de bola, rebatidas, salto e levantamento de peso podem ser combinados em um único fator, como capacidade atlética geral. Normalmente, em uma matriz de item por pessoa, os fatores são selecionados agrupando itens relacionados. Na técnica de análise de fator Q, a matriz é transposta e os fatores são criados agrupando pessoas relacionadas. Por exemplo, liberais, libertários, conservadores e socialistas podem formar grupos separados.
- Identificação de grupos de variáveis inter-relacionadas, para ver como se relacionam entre si. Por exemplo, Carroll usou a análise fatorial para construir sua Teoria dos Três Estratos . Ele descobriu que um fator chamado "percepção visual ampla" se relaciona com o quão bom um indivíduo é nas tarefas visuais. Ele também encontrou um fator de "percepção auditiva ampla", relacionado à capacidade da tarefa auditiva. Além disso, ele encontrou um fator global, denominado "g" ou inteligência geral, que se relaciona tanto com a "percepção visual ampla" quanto com a "percepção auditiva ampla". Isso significa que alguém com um "g" alto provavelmente terá uma alta capacidade de "percepção visual" e uma alta capacidade de "percepção auditiva", e que "g", portanto, explica uma boa parte do motivo pelo qual alguém é bom ou ruim em ambos esses domínios.
Desvantagens
- "... cada orientação é igualmente aceitável matematicamente. Mas diferentes teorias fatoriais provaram ser diferentes tanto em termos das orientações dos eixos fatoriais para uma determinada solução quanto em termos de qualquer outra coisa, de modo que o ajuste do modelo não se mostrou útil em distinguir entre as teorias. " (Sternberg, 1977). Isso significa que todas as rotações representam diferentes processos subjacentes, mas todas as rotações são resultados igualmente válidos da otimização da análise fatorial padrão. Portanto, é impossível escolher a rotação adequada usando apenas a análise fatorial.
- A análise fatorial pode ser tão boa quanto os dados permitirem. Em psicologia, onde os pesquisadores muitas vezes dependem de medidas menos válidas e confiáveis, como auto-relatos, isso pode ser problemático.
- A interpretação da análise fatorial baseia-se no uso de uma "heurística", que é uma solução "conveniente mesmo que não seja absolutamente verdadeira". Mais de uma interpretação pode ser feita dos mesmos dados fatorados da mesma maneira, e a análise fatorial não pode identificar causalidade.
Análise fatorial exploratória (EFA) versus análise de componentes principais (PCA)
A análise fatorial está relacionada à análise de componentes principais (PCA), mas as duas não são idênticas. Tem havido controvérsia significativa na área sobre as diferenças entre as duas técnicas. O PCA pode ser considerado uma versão mais básica da análise fatorial exploratória (EFA) que foi desenvolvida nos primeiros dias antes do advento dos computadores de alta velocidade. Tanto a PCA quanto a análise fatorial visam reduzir a dimensionalidade de um conjunto de dados, mas as abordagens adotadas para isso são diferentes para as duas técnicas. A análise fatorial é claramente desenhada com o objetivo de identificar certos fatores não observáveis a partir das variáveis observadas, ao passo que a PCA não aborda diretamente esse objetivo; na melhor das hipóteses, o PCA fornece uma aproximação aos fatores necessários. Do ponto de vista da análise exploratória, os autovalores da PCA são carregamentos de componentes inflados, ou seja, contaminados com variância do erro.
Embora EFA e PCA sejam tratados como técnicas sinônimos em alguns campos da estatística, isso tem sido criticado. A análise fatorial "lida com a suposição de uma estrutura causal subjacente : [ela] assume que a covariação nas variáveis observadas é devida à presença de uma ou mais variáveis latentes (fatores) que exercem influência causal sobre essas variáveis observadas". Em contraste, o PCA não assume nem depende dessa relação causal subjacente. Os pesquisadores argumentaram que as distinções entre as duas técnicas podem significar que há benefícios objetivos por preferir uma em relação à outra com base no objetivo analítico. Se o modelo fatorial for formulado incorretamente ou as suposições não forem atendidas, a análise fatorial dará resultados errôneos. A análise fatorial foi usada com sucesso onde a compreensão adequada do sistema permite boas formulações de modelos iniciais. O PCA emprega uma transformação matemática nos dados originais sem suposições sobre a forma da matriz de covariância. O objetivo do PCA é determinar combinações lineares das variáveis originais e selecionar algumas que podem ser usadas para resumir o conjunto de dados sem perder muitas informações.
Argumentos que contrastam PCA e EFA
Fabrigar et al. (1999) abordam uma série de razões usadas para sugerir que PCA não é equivalente à análise fatorial:
- Às vezes, é sugerido que o PCA é computacionalmente mais rápido e requer menos recursos do que a análise fatorial. Fabrigar et al. sugerem que recursos de computador prontamente disponíveis tornaram essa preocupação prática irrelevante.
- A PCA e a análise fatorial podem produzir resultados semelhantes. Este ponto também é abordado por Fabrigar et al .; em certos casos, em que as comunalidades são baixas (por exemplo, 0,4), as duas técnicas produzem resultados divergentes. Na verdade, Fabrigar et al. argumentam que, nos casos em que os dados correspondem às suposições do modelo de fator comum, os resultados da PCA são imprecisos.
- Existem certos casos em que a análise fatorial leva a 'casos de Heywood'. Estas abrangem situações em que se estima que 100% ou mais da variância em uma variável medida seja contabilizada pelo modelo. Fabrigar et al. sugerem que esses casos são realmente informativos para o pesquisador, indicando um modelo especificado incorretamente ou uma violação do modelo de fator comum. A falta de casos de Heywood na abordagem PCA pode significar que tais questões passam despercebidas.
- Os pesquisadores obtêm informações extras de uma abordagem PCA, como a pontuação de um indivíduo em um determinado componente; essas informações não são obtidas a partir da análise fatorial. No entanto, como Fabrigar et al. afirmam, o objetivo típico da análise fatorial - ou seja, determinar os fatores responsáveis pela estrutura das correlações entre as variáveis medidas - não requer o conhecimento das pontuações dos fatores e, portanto, essa vantagem é negada. Também é possível calcular pontuações fatoriais a partir de uma análise fatorial.
Variância versus covariância
A análise fatorial leva em consideração o erro aleatório inerente à medição, enquanto o PCA não o faz. Este ponto é exemplificado por Brown (2009), que indicou que, no que diz respeito às matrizes de correlação envolvidas nos cálculos:
"No PCA, 1,00s são colocados na diagonal, o que significa que toda a variância na matriz deve ser contabilizada (incluindo a variância única para cada variável, a variância comum entre as variáveis e a variância do erro). Isso seria, portanto, por definição , inclua toda a variância nas variáveis. Em contraste, em EFA, as comunalidades são colocadas na diagonal, o que significa que apenas a variância compartilhada com outras variáveis deve ser contabilizada (excluindo a variância única de cada variável e a variância do erro). iria, portanto, por definição, incluir apenas a variância que é comum entre as variáveis. "
- Brown (2009), Análise de componentes principais e análise fatorial exploratória - Definições, diferenças e escolhas
Por esse motivo, Brown (2009) recomenda o uso da análise fatorial quando existem ideias teóricas sobre as relações entre as variáveis, enquanto a PCA deve ser usada se o objetivo do pesquisador for explorar padrões em seus dados.
Diferenças de procedimento e resultados
As diferenças entre a PCA e a análise fatorial (FA) são ainda ilustradas por Suhr (2009):
- PCA resulta em componentes principais que respondem por uma quantidade máxima de variância para variáveis observadas; FA é responsável pela variação comum nos dados.
- PCA insere uns nas diagonais da matriz de correlação; FA ajusta as diagonais da matriz de correlação com os fatores únicos.
- PCA minimiza a soma da distância perpendicular quadrada ao eixo do componente; FA estima os fatores que influenciam as respostas nas variáveis observadas.
- As pontuações dos componentes no PCA representam uma combinação linear das variáveis observadas ponderadas por autovetores ; as variáveis observadas em FA são combinações lineares dos fatores subjacentes e únicos.
- No PCA, os componentes produzidos são ininterpretáveis, ou seja, eles não representam 'construções' subjacentes; em FA, as construções subjacentes podem ser rotuladas e prontamente interpretadas, dadas uma especificação de modelo precisa.
Em marketing
As etapas básicas são:
- Identifique os atributos mais importantes que os consumidores usam para avaliar produtos nesta categoria.
- Use técnicas quantitativas de pesquisa de marketing (como pesquisas ) para coletar dados de uma amostra de clientes potenciais sobre suas classificações de todos os atributos do produto.
- Insira os dados em um programa estatístico e execute o procedimento de análise fatorial. O computador produzirá um conjunto de atributos subjacentes (ou fatores).
- Use esses fatores para construir mapas de percepção e outros dispositivos de posicionamento do produto .
Coleta de informações
A etapa de coleta de dados geralmente é feita por profissionais de pesquisa de marketing. As perguntas da pesquisa pedem ao entrevistado para avaliar uma amostra de produto ou descrições de conceitos de produto em uma variedade de atributos. Em qualquer lugar de cinco a vinte atributos são escolhidos. Eles podem incluir coisas como: facilidade de uso, peso, precisão, durabilidade, cores, preço ou tamanho. Os atributos escolhidos irão variar dependendo do produto em estudo. A mesma pergunta é feita sobre todos os produtos do estudo. Os dados de vários produtos são codificados e inseridos em um programa estatístico como R , SPSS , SAS , Stata , STATISTICA , JMP e SYSTAT.
Análise
A análise isolará os fatores subjacentes que explicam os dados usando uma matriz de associações. A análise fatorial é uma técnica de interdependência. O conjunto completo de relacionamentos interdependentes é examinado. Não há especificação de variáveis dependentes, variáveis independentes ou causalidade. A análise fatorial assume que todos os dados de classificação em atributos diferentes podem ser reduzidos a algumas dimensões importantes. Essa redução é possível porque alguns atributos podem estar relacionados entre si. A classificação dada a qualquer atributo é parcialmente o resultado da influência de outros atributos. O algoritmo estatístico desconstrói a classificação (chamada de pontuação bruta) em seus vários componentes e reconstrói as pontuações parciais em pontuações de fatores subjacentes. O grau de correlação entre a pontuação bruta inicial e a pontuação final do fator é chamado de carregamento fatorial .
Vantagens
- Os atributos objetivos e subjetivos podem ser usados, desde que os atributos subjetivos possam ser convertidos em pontuações.
- A análise fatorial pode identificar dimensões latentes ou construções que a análise direta não pode.
- É fácil e barato.
Desvantagens
- A utilidade depende da capacidade dos pesquisadores de coletar um conjunto suficiente de atributos do produto. Se atributos importantes são excluídos ou negligenciados, o valor do procedimento é reduzido.
- Se os conjuntos de variáveis observadas forem muito semelhantes entre si e distintos de outros itens, a análise fatorial atribuirá um único fator a eles. Isso pode obscurecer fatores que representam relacionamentos mais interessantes.
- Fatores de nomenclatura podem exigir conhecimento de teoria porque atributos aparentemente diferentes podem se correlacionar fortemente por razões desconhecidas.
Em ciências físicas e biológicas
A análise fatorial também tem sido amplamente utilizada nas ciências físicas, como geoquímica , hidroquímica , astrofísica e cosmologia , bem como nas ciências biológicas, como ecologia , biologia molecular , neurociência e bioquímica .
Na gestão da qualidade da água subterrânea, é importante relacionar a distribuição espacial de diferentes parâmetros químicos a diferentes fontes possíveis, que têm diferentes assinaturas químicas. Por exemplo, uma mina de sulfeto provavelmente está associada a altos níveis de acidez, sulfatos dissolvidos e metais de transição. Essas assinaturas podem ser identificadas como fatores por meio da análise fatorial do modo-R, e a localização de possíveis fontes pode ser sugerida contornando as pontuações dos fatores.
Na geoquímica , diferentes fatores podem corresponder a diferentes associações minerais e, portanto, à mineralização.
Na análise de microarray
A análise de fator pode ser usada para resumir dados de microarranjos de DNA de oligonucleotídeo de alta densidade em nível de sonda para Affymetrix GeneChips. Nesse caso, a variável latente corresponde à concentração de RNA em uma amostra.
Implementação
A análise fatorial foi implementada em vários programas de análise estatística desde a década de 1980:
- BMDP
- JMP (software estatístico)
- Mplus (software estatístico)]
- Python : módulo Scikit-learn
- R (com a função de base factanal ou função fa no pacote psych ). As rotações são implementadas no pacote GPArotation R.
- SAS (usando PROC FACTOR ou PROC CALIS)
- SPSS
- Stata
Veja também
Referências
Leitura adicional
- Child, Dennis (2006), The Essentials of Factor Analysis (3ª ed.), Continuum International , ISBN 978-0-8264-8000-2.
- Fabrigar, LR; Wegener, DT; MacCallum, RC; Strahan, EJ (setembro de 1999). "Avaliando o uso da análise fatorial exploratória na pesquisa psicológica". Métodos psicológicos . 4 (3): 272–299. doi : 10.1037 / 1082-989X.4.3.272 .
- BT Gray (1997) High-Order Factor Analysis (artigo de conferência)
- Jennrich, Robert I., "Rotation to Simple Loadings Using Component Loss Function: The Oblique Case" , Psychometrika , Vol. 71, No. 1, pp. 173–191, março de 2006.
- Katz, Jeffrey Owen e Rohlf, F. James. Plano de função do produto primário: uma rotação oblíqua para uma estrutura simples. Multivariate Behavioral Research , abril de 1975, Vol. 10, pp. 219–232.
- Katz, Jeffrey Owen e Rohlf, F. James. Plano de funções: uma nova abordagem para a rotação de estruturas simples. Psychometrika , março de 1974, vol. 39, No. 1, pp. 37–51.
- Katz, Jeffrey Owen e Rohlf, F. James. Análise de cluster de ponto de função. Systematic Zoology , setembro de 1973, vol. 22, No. 3, pp. 295-301.
- Mulaik, SA (2010), Foundations of Factor Analysis , Chapman & Hall.
- Pregador, KJ; MacCallum, RC (2003). "Reparando a Máquina de Análise de Fator Elétrico de Tom Swift" (PDF) . Compreendendo as estatísticas . 2 (1): 13–43. doi : 10.1207 / S15328031US0201_02 . hdl : 1808/1492 .
- J.Schmid e JM Leiman (1957). O desenvolvimento de soluções de fator hierárquico. Psychometrika , 22 (1), 53-61.
- Thompson, B. (2004), Análise Fatorial Exploratória e Confirmatória: Compreensão de conceitos e aplicações , Washington DC: American Psychological Association , ISBN 978-1591470939.
- Hans-Georg Wolff, Katja Preising (2005) Explorando item e estrutura de fator de ordem superior com a solução schmid-leiman: códigos de sintaxe para métodos de pesquisa de comportamento SPSS e SAS , instrumentos e computadores , 37 (1), 48-58
links externos
- Um guia para iniciantes em análise fatorial
- Análise Fatorial Exploratória. A Book Manuscript de Tucker, L. & MacCallum R. (1993). Recuperado em 8 de junho de 2006, em: [1]
- Garson, G. David, "Factor Analysis," from Statnotes: Topics in Multivariate Analysis . Obtido em 13 de abril de 2009 de StatNotes: Tópicos em Análise Multivariada, de G. David Garson na Universidade Estadual da Carolina do Norte, Programa de Administração Pública
- Análise Fatorial em 100 - material de conferência
- FARMS - Factor Analysis for Robust Microarray Summarization, an R package














































































![{\ displaystyle \ varepsilon ^ {2} = \ sum _ {a \ neq b} \ left [\ sum _ {i} z_ {ai} z_ {bi} - \ sum _ {j} \ ell _ {aj} \ ell _ {bj} \ right] ^ {2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d0ee958e2ff337f289adad14c1757c7bea9462ea)






















