Integração de contorno - Contour integration

No campo matemático da análise complexa , a integração do contorno é um método de avaliação de certas integrais ao longo de caminhos no plano complexo .

A integração de contorno está intimamente relacionada ao cálculo de resíduos , um método de análise complexa .

Um uso para integrais de contorno é a avaliação de integrais ao longo da linha real que não são facilmente encontradas usando apenas métodos de variáveis reais.

Os métodos de integração de contorno incluem:

integração direta de uma função avaliada complexa ao longo de uma curva no plano complexo (um contorno );
aplicação da fórmula integral de Cauchy ; e
aplicação do teorema do resíduo .

Um método pode ser usado, ou uma combinação desses métodos, ou vários processos de limitação, com o propósito de encontrar essas integrais ou somas.

Curvas no plano complexo

Na análise complexa, um contorno é um tipo de curva no plano complexo . Na integração de contornos, os contornos fornecem uma definição precisa das curvas nas quais uma integral pode ser adequadamente definida. Uma curva no plano complexo é definida como uma função contínua a partir de um intervalo fechado da linha verdadeiro para o plano complexo: $z : [a, b] \to C$ .

Esta definição de curva coincide com a noção intuitiva de curva, mas inclui uma parametrização por uma função contínua a partir de um intervalo fechado. Essa definição mais precisa nos permite considerar quais propriedades uma curva deve ter para ser útil para a integração. Nas subseções a seguir, restringimos o conjunto de curvas que podemos integrar para incluir apenas aquelas que podem ser construídas a partir de um número finito de curvas contínuas que podem receber uma direção. Além disso, restringiremos as "peças" de se cruzarem, e exigimos que cada peça tenha uma derivada contínua finita (não desaparecida). Esses requisitos correspondem a exigir que consideremos apenas as curvas que podem ser traçadas, como por uma caneta, em uma sequência de traços regulares e constantes, que param apenas para iniciar um novo trecho da curva, tudo sem pegar na caneta.

Curvas suaves direcionadas

Os contornos são frequentemente definidos em termos de curvas suaves direcionadas. Eles fornecem uma definição precisa de uma "peça" de uma curva suave, da qual um contorno é feito.

Uma curva suave é uma curva $z : [a, b] \to C$ com uma derivada contínua não-evanescente, de modo que cada ponto é percorrido apenas uma vez ( $z$ é um para um), com a possível exceção de uma curva tal que os pontos finais correspondem ( $z (a) = z (b)$ ). No caso em que os pontos finais correspondem, a curva é chamada de fechada, e a função deve ser um-para-um em todos os outros lugares e a derivada deve ser contínua no ponto identificado ( $z' (a) = z' (b)$ ) . Uma curva suave que não é fechada costuma ser chamada de arco suave.

A parametrização de uma curva fornece uma ordem natural de pontos na curva: $z (x)$ vem antes de $z (y)$ se $x < y$ . Isso leva à noção de uma curva suave direcionada . É mais útil considerar curvas independentes da parametrização específica. Isso pode ser feito considerando classes de equivalência de curvas suaves com a mesma direção. Uma curva suave direcionada pode então ser definida como um conjunto ordenado de pontos no plano complexo que é a imagem de alguma curva suave em sua ordem natural (de acordo com a parametrização). Observe que nem todas as ordens dos pontos são a ordem natural de uma curva suave. Na verdade, uma dada curva suave tem apenas duas dessas ordenações. Além disso, uma única curva fechada pode ter qualquer ponto como sua extremidade, enquanto um arco suave tem apenas duas opções para suas extremidades.

Contornos

Contornos são a classe de curvas nas quais definimos a integração dos contornos. Um contorno é uma curva direcionada que é composta de uma sequência finita de curvas suaves direcionadas cujos pontos finais são combinados para fornecer uma única direção. Isso requer que a sequência de curvas $γ 1,\dots, γ n$ seja tal que o ponto terminal de $γ i$ coincida com o ponto inicial de $γ i +1$ , $\forall i, 1 \leq i < n$ . Isso inclui todas as curvas suaves direcionadas. Além disso, um único ponto no plano complexo é considerado um contorno. O símbolo + é freqüentemente usado para denotar a junção de curvas para formar uma nova curva. Assim, poderíamos escrever um contorno $Γ$ que é feito de $n$ curvas como

{\ displaystyle \ Gamma = \ gamma _ {1} + \ gamma _ {2} + \ cdots + \ gamma _ {n}.}

Integrais de contorno

A integral de contorno de uma função complexa $f : C \to C$ é uma generalização da integral para funções de valor real. Para funções contínuas no plano complexo , a integral de contorno pode ser definida em analogia à integral de linha , primeiro definindo a integral ao longo de uma curva suave direcionada em termos de uma integral sobre um parâmetro de valor real. Uma definição mais geral pode ser dada em termos de partições do contorno em analogia com a partição de um intervalo e a integral de Riemann . Em ambos os casos, a integral sobre um contorno é definida como a soma das integrais sobre as curvas suaves direcionadas que constituem o contorno.

Para funções contínuas

Para definir a integral de contorno dessa maneira, deve-se primeiro considerar a integral, sobre uma variável real, de uma função de valor complexo. Seja $f : R \to C$ uma função de valor complexo de uma variável real, $t$ . As partes reais e imaginárias da $f$ são frequentemente denotado como $u (t)$ e $v (t)$ , respectivamente, de modo que

{\ displaystyle f (t) = u (t) + iv (t).}

Então, a integral da função de valor complexo

f

no intervalo

[a, b]

é dada por

{\ displaystyle {\ begin {alinhado} \ int _ {a} ^ {b} f (t) \, dt & = \ int _ {a} ^ {b} {\ big (} u (t) + iv (t ) {\ big)} \, dt \\ & = \ int _ {a} ^ {b} u (t) \, dt + i \ int _ {a} ^ {b} v (t) \, dt. \ end {alinhado}}}

Seja $f : C \to C$ uma função contínua na curva suave direcionada $γ$ . Seja $z : R \to C$ qualquer parametrização de $γ$ que seja consistente com sua ordem (direção). Então a integral ao longo de $γ$ é denotada

{\ displaystyle \ int _ {\ gamma} f (z) \, dz \,}

e é dado por

{\ displaystyle \ int _ {\ gamma} f (z) \, dz = \ int _ {a} ^ {b} f {\ big (} \ gamma (t) {\ big)} \ gamma '(t) \, dt.}

Esta definição está bem definida. Ou seja, o resultado é independente da parametrização escolhida. No caso em que a integral real no lado direito não existe, diz-se que a integral ao longo de $γ$ não existe.

Como uma generalização da integral de Riemann

A generalização da integral de Riemann para funções de uma variável complexa é feita em completa analogia com sua definição para funções a partir dos números reais. A partição de uma curva suave direcionada $γ$ é definida como um conjunto finito e ordenado de pontos em $γ$ . A integral sobre a curva é o limite de somas finitas de valores de função, tomadas nos pontos da partição, no limite que a distância máxima entre quaisquer dois pontos sucessivos na partição (no plano complexo bidimensional), também conhecido como a malha, vai para zero.

Métodos diretos

Os métodos diretos envolvem o cálculo da integral por meio de métodos semelhantes aos do cálculo de integrais de linha no cálculo multivariado. Isso significa que usamos o seguinte método:

parametrizando o contorno
O contorno é parametrizado por uma função de valor complexo diferenciável de variáveis reais, ou o contorno é dividido em pedaços e parametrizado separadamente.
substituição da parametrização no integrando
Substituir a parametrização no integrando transforma a integral em uma integral de uma variável real.
avaliação direta
A integral é avaliada em um método semelhante a uma integral de variável real.

Exemplo

Um resultado fundamental na análise complexa é que a integral de contorno de $.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num,.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0 0.1em}.mw-parser-output .sfrac .den{border-top:1px solid}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px} 1/z$ é $2π i$ , onde o caminho do contorno é considerado o círculo unitário percorrido no sentido anti-horário (ou qualquer curva de Jordan orientada positivamente em torno de 0). No caso do círculo unitário, há um método direto para avaliar a integral

{\ displaystyle \ oint _ {C} {\ frac {1} {z}} \, dz.}

Ao avaliar essa integral, use o círculo unitário $| z | = 1$ como contorno, parametrizado por $z (t) = e it$ , com $t \in [0, 2π]$ , então $dz / dt = isto é$ e

{\ displaystyle \ oint _ {C} {\ frac {1} {z}} \, dz = \ int _ {0} ^ {2 \ pi} {\ frac {1} {e ^ {it}}} ie ^ {it} \, dt = i \ int _ {0} ^ {2 \ pi} 1 \, dt = i \, t {\ Big |} _ {0} ^ {2 \ pi} = \ left (2 \ pi -0 \ right) i = 2 \ pi i.}

que é o valor da integral.

Aplicações de teoremas integrais

Aplicações de teoremas integrais também são freqüentemente usadas para avaliar a integral de contorno ao longo de um contorno, o que significa que a integral de valor real é calculada simultaneamente com o cálculo da integral de contorno.

Teoremas integrais, como a fórmula integral de Cauchy ou o teorema do resíduo são geralmente usados no seguinte método:

um contorno específico é escolhido:
O contorno é escolhido de forma que siga a parte do plano complexo que descreve a integral de valor real, e também inclui as singularidades do integrando, de forma que a aplicação da fórmula da integral de Cauchy ou teorema do resíduo seja possível
aplicação do teorema integral de Cauchy
A integral é reduzida a apenas uma integração em torno de um pequeno círculo em torno de cada pólo.
aplicação da fórmula integral de Cauchy ou teorema do resíduo
A aplicação dessas fórmulas integrais nos dá um valor para a integral em torno de todo o contorno.
divisão do contorno em um contorno ao longo da parte real e parte imaginária
Todo o contorno pode ser dividido no contorno que segue a parte do plano complexo que descreve a integral de valor real conforme escolhida anteriormente (chame-a de $R$ ), e a integral que cruza o plano complexo (chame-a de $I$ ). A integral sobre todo o contorno é a soma da integral sobre cada um desses contornos.
demonstração de que a integral que cruza o plano complexo não desempenha nenhum papel na soma
Se a integral $I$ pode ser mostrada como zero, ou se a integral de valor real que é buscada é imprópria, então se demonstrarmos que a integral $I,$ conforme descrito acima, tende a 0, a integral ao longo de $R$ tenderá para a integral em torno de contorno $R + I$ .
conclusão
Se pudermos mostrar a etapa acima, então podemos calcular diretamente $R$ , a integral de valor real.

Exemplo 1

Considere a integral

{\ displaystyle \ int _ {- \ infty} ^ {\ infty} {\ frac {1} {\ left (x ^ {2} +1 \ right) ^ {2}}} \, dx,}

Para avaliar essa integral, olhamos para a função de valor complexo

{\ displaystyle f (z) = {\ frac {1} {\ left (z ^ {2} +1 \ right) ^ {2}}}}

que tem singularidades em $i$ e $- i$ . Nós escolhemos um contorno que vai colocar o integrante valor real, aqui um semicírculo com diâmetro limite na linha real (indo de, digamos, $- um$ a $um$ ) será conveniente. Chame esse contorno $C$ .

Existem duas maneiras de proceder, usando a fórmula integral de Cauchy ou pelo método dos resíduos:

Usando a fórmula integral de Cauchy

Observe que:

{\ displaystyle \ oint _ {C} f (z) \, dz = \ int _ {- a} ^ {a} f (z) \, dz + \ int _ {\ text {Arc}} f (z) \ , dz}

portanto

{\ displaystyle \ int _ {- a} ^ {a} f (z) \, dz = \ oint _ {C} f (z) \, dz- \ int _ {\ text {Arc}} f (z) \, dz}

Além disso, observe que

{\ displaystyle f (z) = {\ frac {1} {\ left (z ^ {2} +1 \ right) ^ {2}}} = {\ frac {1} {(z + i) ^ {2 } (zi) ^ {2}}}.}

Uma vez que a única singularidade no contorno é aquela em $i$ , então podemos escrever

{\ displaystyle f (z) = {\ frac {\ frac {1} {(z + i) ^ {2}}} {(zi) ^ {2}}},}

que coloca a função na forma de aplicação direta da fórmula. Então, usando a fórmula integral de Cauchy,

{\ displaystyle \ oint _ {C} f (z) \, dz = \ oint _ {C} {\ frac {\ frac {1} {(z + i) ^ {2}}} {(zi) ^ { 2}}} \, dz = 2 \ pi i \, \ left. {\ Frac {d} {dz}} {\ frac {1} {(z + i) ^ {2}}} \ right | _ { z = i} = 2 \ pi i \ left [{\ frac {-2} {(z + i) ^ {3}}} \ right] _ {z = i} = {\ frac {\ pi} {2 }}}

Tomamos a primeira derivada, nas etapas acima, porque o pólo é um pólo de segunda ordem. Ou seja, $(z - i)$ é levado à segunda potência, então empregamos a primeira derivada de $f (z)$ . Se fosse $(z - i)$ levado à terceira potência, usaríamos a segunda derivada e dividiríamos por 2 !, etc. O caso de $(z - i)$ à primeira potência corresponde a uma derivada de ordem zero - apenas $f (z) em$ si.

Precisamos mostrar que a integral sobre o arco do semicírculo tende a zero como $a \to \infty$ , usando o lema de estimação

{\ displaystyle \ left | \ int _ {\ text {Arc}} f (z) \, dz \ right | \ leq ML}

onde $M$ é um limite superior em $| f (z) |$ ao longo do arco e $L$ o comprimento do arco. Agora,

{\ displaystyle \ left | \ int _ {\ text {Arc}} f (z) \, dz \ right | \ leq {\ frac {a \ pi} {\ left (a ^ {2} -1 \ right) ^ {2}}} \ a 0 {\ text {as}} a \ a \ infty.}

Então

{\ displaystyle \ int _ {- \ infty} ^ {\ infty} {\ frac {1} {\ left (x ^ {2} +1 \ right) ^ {2}}} \, dx = \ int _ { - \ infty} ^ {\ infty} f (z) \, dz = \ lim _ {a \ to + \ infty} \ int _ {- a} ^ {a} f (z) \, dz = {\ frac {\ pi} {2}}. \ quad \ square}

Usando o método de resíduos

Considere a série de Laurent de $f (z)$ sobre $i$ , a única singularidade que precisamos considerar. Então temos

{\ displaystyle f (z) = {\ frac {-1} {4 (zi) ^ {2}}} + {\ frac {-i} {4 (zi)}} + {\ frac {3} {16 }} + {\ frac {i} {8}} (zi) + {\ frac {-5} {64}} (zi) ^ {2} + \ cdots}

(Veja a amostra de cálculo de Laurent da série de Laurent para a derivação desta série.)

É claro pela inspeção que o resíduo é $- eu / 4$ , então, pelo teorema do resíduo , temos

{\ displaystyle \ oint _ {C} f (z) \, dz = \ oint _ {C} {\ frac {1} {\ left (z ^ {2} +1 \ right) ^ {2}}} \ , dz = 2 \ pi i \, \ operatorname {Res} _ {z = i} f (z) = 2 \ pi i \ left (- {\ frac {i} {4}} \ right) = {\ frac {\ pi} {2}} \ quad \ square}

Assim, obtemos o mesmo resultado de antes.

Nota de contorno

Como um aparte, uma questão pode surgir se não tomamos o semicírculo para incluir a outra singularidade, incluindo $- i$ . Para que a integral ao longo do eixo real se mova na direção correta, o contorno deve se deslocar no sentido horário, ou seja, em uma direção negativa, invertendo o sinal da integral geral.

Isso não afeta o uso do método de resíduos por série.

Exemplo 2 - distribuição de Cauchy

O integral

{\ displaystyle \ int _ {- \ infty} ^ {\ infty} {\ frac {e ^ {itx}} {x ^ {2} +1}} \, dx}

(que surge na teoria da probabilidade como um múltiplo escalar da função característica da distribuição de Cauchy ) resiste às técnicas de cálculo elementar . Iremos avaliá-lo expressando-o como um limite de integrais de contorno ao longo do contorno $C$ que vai ao longo da linha real de $- a$ para $a$ e então no sentido anti-horário ao longo de um semicírculo centrado em 0 de $a$ para $- a$ . Tomar $um$ para ser maior do que 1, de modo que o imaginário unidade $i$ é colocado dentro da curva. A integral de contorno é

{\ displaystyle \ int _ {C} {\ frac {e ^ {itz}} {z ^ {2} +1}} \, dz.}

Como $e itz$ é uma função inteira (sem singularidades em nenhum ponto do plano complexo), essa função tem singularidades apenas onde o denominador $z 2 + 1$ é zero. Como $z 2 + 1 = (z + i) (z - i)$ , isso acontece apenas onde $z = i$ ou $z = - i$ . Apenas um desses pontos está na região delimitada por este contorno. O resíduo de $f (z)$ em $z = i$ é

{\ displaystyle \ lim _ {z \ to i} (zi) f (z) = \ lim _ {z \ to i} (zi) {\ frac {e ^ {itz}} {z ^ {2} +1 }} = \ lim _ {z \ to i} (zi) {\ frac {e ^ {itz}} {(zi) (z + i)}} = \ lim _ {z \ to i} {\ frac { e ^ {itz}} {z + i}} = {\ frac {e ^ {- t}} {2i}}.}

De acordo com o teorema do resíduo , então, temos

{\ displaystyle \ int _ {C} f (z) \, dz = 2 \ pi i \ operatorname {Res} _ {z = i} f (z) = 2 \ pi i {\ frac {e ^ {- t }} {2i}} = \ pi e ^ {- t}.}

O contorno $C$ pode ser dividido em uma parte "reta" e um arco curvo, de modo que

{\ displaystyle \ int _ {\ text {straight}} + \ int _ {\ text {arc}} = \ pi e ^ {- t},}

e assim

{\ displaystyle \ int _ {- a} ^ {a} = \ pi e ^ {- t} - \ int _ {\ text {arc}}.}

De acordo com o lema de Jordan , se $t > 0,$ então

{\ displaystyle \ int _ {\ text {arc}} {\ frac {e ^ {itz}} {z ^ {2} +1}} \, dz \ rightarrow 0 {\ mbox {as}} a \ rightarrow \ infty.}

Portanto, se $t > 0,$ então

{\ displaystyle \ int _ {- \ infty} ^ {\ infty} {\ frac {e ^ {itx}} {x ^ {2} +1}} \, dx = \ pi e ^ {- t}.}

Um argumento semelhante com um arco que serpenteia $- i em$ vez de $i$ mostra que se $t <0,$ então

{\ displaystyle \ int _ {- \ infty} ^ {\ infty} {\ frac {e ^ {itx}} {x ^ {2} +1}} \, dx = \ pi e ^ {t},}

e finalmente temos isso:

{\ displaystyle \ int _ {- \ infty} ^ {\ infty} {\ frac {e ^ {itx}} {x ^ {2} +1}} \, dx = \ pi e ^ {- | t |} . \ quad \ square}

(Se $t = 0,$ então a integral resulta imediatamente em métodos de cálculo com valor real e seu valor é $π$ .)

Exemplo 3 - integrais trigonométricas

Certas substituições podem ser feitas para integrais envolvendo funções trigonométricas , então a integral é transformada em uma função racional de uma variável complexa e então os métodos acima podem ser usados para avaliar a integral.

Por exemplo, considere

{\ displaystyle \ int _ {- \ pi} ^ {\ pi} {\ frac {1} {1 + 3 (\ cos t) ^ {2}}} \, dt.}

Procuramos fazer uma substituição de $z = e it$ . Agora, lembre-se

{\ displaystyle \ cos t = {\ frac {1} {2}} \ left (e ^ {it} + e ^ {- it} \ right) = {\ frac {1} {2}} \ left (z + {\ frac {1} {z}} \ right)}

e

{\ displaystyle {\ frac {dz} {dt}} = iz, \ dt = {\ frac {dz} {iz}}.}

Tomando $C$ como o círculo unitário, substituímos para obter:

{\ displaystyle {\ begin {alinhados} \ oint _ {C} {\ frac {1} {1 + 3 \ left ({\ frac {1} {2}} \ left (z + {\ frac {1} {z }} \ right) \ right) ^ {2}}} \, {\ frac {dz} {iz}} & = \ oint _ {C} {\ frac {1} {1 + {\ frac {3} { 4}} \ left (z + {\ frac {1} {z}} \ right) ^ {2}}} {\ frac {1} {iz}} \, dz \\ & = \ oint _ {C} { \ frac {-i} {z + {\ frac {3} {4}} z \ left (z + {\ frac {1} {z}} \ right) ^ {2}}} \, dz \\ & = - i \ oint _ {C} {\ frac {dz} {z + {\ frac {3} {4}} z \ left (z ^ {2} +2 + {\ frac {1} {z ^ {2}} } \ right)}} \\ & = - i \ oint _ {C} {\ frac {dz} {z + {\ frac {3} {4}} \ left (z ^ {3} + 2z + {\ frac { 1} {z}} \ right)}} \\ & = - i \ oint _ {C} {\ frac {dz} {{\ frac {3} {4}} z ^ {3} + {\ frac { 5} {2}} z + {\ frac {3} {4z}}}} \\ & = - i \ oint _ {C} {\ frac {4} {3z ^ {3} + 10z + {\ frac {3 } {z}}}} \, dz \\ & = - 4i \ oint _ {C} {\ frac {dz} {3z ^ {3} + 10z + {\ frac {3} {z}}}} \\ & = - 4i \ oint _ {C} {\ frac {z} {3z ^ {4} + 10z ^ {2} +3}} \, dz \\ & = - 4i \ oint _ {C} {\ frac {z} {3 \ left (z + {\ sqrt {3}} i \ right) \ left (z - {\ sqrt {3}} i \ right) \ left (z + {\ frac {i} {\ sqrt { 3}}} \ direita) \ esquerda (z - {\ frac {i} {\ sqrt {3}}} \ direita)}} \, dz \\ & = - {\ frac {4i} {3}} \ oint _ {C} {\ frac {z} {\ left (z + {\ sqrt {3}} i \ right) \ left (z - {\ sqrt {3}} i \ right) \ left (z + {\ frac {eu}{ \ sqrt {3}}} \ right) \ left (z - {\ frac {i} {\ sqrt {3}}} \ right)}} \, dz. \ end {alinhado}}}

As singularidades a serem consideradas estão em: Seja $C$ $1$ um pequeno círculo em volta e $C$ $2$ um pequeno círculo em volta. Então chegamos ao seguinte: ${\ displaystyle {\ tfrac {\ pm i} {\ sqrt {3}}}.}$ ${\ displaystyle {\ tfrac {i} {\ sqrt {3}}},}$ ${\ displaystyle {\ tfrac {-i} {\ sqrt {3}}}.}$

{\ displaystyle {\ begin {alinhados} & - {\ frac {4i} {3}} \ left [\ oint _ {C_ {1}} {\ frac {\ frac {z} {\ left (z + {\ sqrt {3}} i \ right) \ left (z - {\ sqrt {3}} i \ right) \ left (z + {\ frac {i} {\ sqrt {3}}} \ right)}} {z- {\ frac {i} {\ sqrt {3}}}}} \, dz + \ oint _ {C_ {2}} {\ frac {\ frac {z} {\ left (z + {\ sqrt {3}} i \ right) \ left (z - {\ sqrt {3}} i \ right) \ left (z - {\ frac {i} {\ sqrt {3}}} \ right)}} {z + {\ frac {i } {\ sqrt {3}}}}} \, dz \ right] \\ = {} & - {\ frac {4i} {3}} \ left [2 \ pi i \ left [{\ frac {z} {\ left (z + {\ sqrt {3}} i \ right) \ left (z - {\ sqrt {3}} i \ right) \ left (z + {\ frac {i} {\ sqrt {3}}} \ right)}} \ right] _ {z = {\ frac {i} {\ sqrt {3}}}} + 2 \ pi i \ left [{\ frac {z} {\ left (z + {\ sqrt { 3}} i \ right) \ left (z - {\ sqrt {3}} i \ right) \ left (z - {\ frac {i} {\ sqrt {3}}} \ right)}} \ right] _ {z = - {\ frac {i} {\ sqrt {3}}}} \ right] \\ = {} & {\ frac {8 \ pi} {3}} \ left [{\ frac {\ frac {i} {\ sqrt {3}}} {\ left ({\ frac {i} {\ sqrt {3}}} + {\ sqrt {3}} i \ right) \ left ({\ frac {i} {\ sqrt {3}}} - {\ sqrt {3}} i \ direita) \ esquerda ({\ frac {i} {\ sqrt {3}}} + {\ frac {i} {\ sqrt {3} }} \ right)}} + {\ frac {- {\ frac {i} {\ sqrt {3}}}} {\ left (- {\ frac {i} {\ sqrt {3}}} + {\ sqrt {3 }} i \ right) \ left (- {\ frac {i} {\ sqrt {3}}} - {\ sqrt {3}} i \ right) \ left (- {\ frac {i} {\ sqrt { 3}}} - {\ frac {i} {\ sqrt {3}}} \ right)}} \ right] \\ = {} & {\ frac {8 \ pi} {3}} \ left [{\ frac {\ frac {i} {\ sqrt {3}}} {\ left ({\ frac {4} {\ sqrt {3}}} i \ right) \ left (- {\ frac {2} {i { \ sqrt {3}}}} \ right) \ left ({\ frac {2} {{\ sqrt {3}} i}} \ right)}} + {\ frac {- {\ frac {i} {\ sqrt {3}}}} {\ left ({\ frac {2} {\ sqrt {3}}} i \ right) \ left (- {\ frac {4} {\ sqrt {3}}} i \ right ) \ left (- {\ frac {2} {\ sqrt {3}}} i \ right)}} \ right] \\ = {} & {\ frac {8 \ pi} {3}} \ left [{ \ frac {\ frac {i} {\ sqrt {3}}} {i \ left ({\ frac {4} {\ sqrt {3}}} \ right) \ left ({\ frac {2} {\ sqrt {3}}} \ right) \ left ({\ frac {2} {\ sqrt {3}}} \ right)}} + {\ frac {- {\ frac {i} {\ sqrt {3}}} } {- i \ left ({\ frac {2} {\ sqrt {3}}} \ right) \ left ({\ frac {4} {\ sqrt {3}}} \ right) \ left ({\ frac {2} {\ sqrt {3}}} \ right)}} \ right] \\ = {} & {\ frac {8 \ pi} {3}} \ left [{\ frac {\ frac {1}} \ sqrt {3}}} {\ left ({\ frac {4} {\ sqrt {3}}} \ right) \ left ({\ frac {2} {\ sqrt {3}}} \ right) \ left ({\ frac {2} {\ sqrt {3}}} \ right)}} + {\ frac {\ frac {1} {\ sqrt {3}}} {\ left ({\ frac {2} {\ sqrt {3}}} \ direita) \ esquerda ({\ frac {4} {\ sqrt {3}}} \ direita) \ esquerda ({\ frac {2} {\ sqrt {3}}} \ direita)}} \ direita] \\ = {} & {\ frac {8 \ pi} {3}} \ left [{\ frac {\ frac {1} {\ sqrt {3}}} {\ frac {16} {3 {\ sqrt {3}} }}} + {\ frac {\ frac {1} {\ sqrt {3}}} {\ frac {16} {3 {\ sqrt {3}}}}} \ right] \\ = {} & {\ frac {8 \ pi} {3}} \ left [{\ frac {3} {16}} + {\ frac {3} {16}} \ right] \\ = {} & \ pi. \ end {alinhados }}}

Exemplo 3a - integrais trigonométricas, o procedimento geral

O método acima pode ser aplicado a todas as integrais do tipo

{\ displaystyle \ int _ {0} ^ {2 \ pi} {\ frac {P {\ big (} \ sin (t), \ sin (2t), \ ldots, \ cos (t), \ cos (2t ), \ ldots {\ big)}} {Q {\ big (} \ sin (t), \ sin (2t), \ ldots, \ cos (t), \ cos (2t), \ ldots {\ big) }}} \, dt}

onde $P$ e $Q$ são polinômios, ou seja, uma função racional em termos trigonométricos está sendo integrada. Observe que os limites de integração também podem ser $π$ e - $π$ , como no exemplo anterior, ou qualquer outro par de pontos de extremidade separados por 2 $π$ .

O truque é usar a substituição $z = e it,$ onde $dz = ou seja, dt$ e, portanto,

{\ displaystyle {\ frac {1} {iz}} \, dz = dt.}

Esta substituição mapeia o intervalo $[0, 2π]$ para o círculo unitário. Além disso,

{\ displaystyle \ sin (kt) = {\ frac {e ^ {ikt} -e ^ {- ikt}} {2i}} = {\ frac {z ^ {k} -z ^ {- k}} {2i }}}

e

{\ displaystyle \ cos (kt) = {\ frac {e ^ {ikt} + e ^ {- ikt}} {2}} = {\ frac {z ^ {k} + z ^ {- k}} {2 }}}

de modo que uma função racional

f (z)

em

z

resulta da substituição, e a integral torna-se

{\ displaystyle \ oint _ {| z | = 1} f (z) {\ frac {1} {iz}} \, dz}

que por sua vez é calculado somando os resíduos de

f (z) 1 / iz

dentro do círculo unitário.

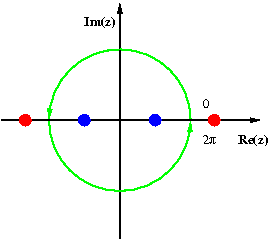
A imagem à direita ilustra isso para

{\ displaystyle I = \ int _ {0} ^ {\ frac {\ pi} {2}} {\ frac {1} {1 + (\ sin t) ^ {2}}} \, dt,}

que agora calculamos. O primeiro passo é reconhecer que

{\ displaystyle I = {\ frac {1} {4}} \ int _ {0} ^ {2 \ pi} {\ frac {1} {1 + (\ sin t) ^ {2}}} \, dt .}

A substituição produz

{\ displaystyle {\ frac {1} {4}} \ oint _ {| z | = 1} {\ frac {4iz} {z ^ {4} -6z ^ {2} +1}} \, dz = \ oint _ {| z | = 1} {\ frac {iz} {z ^ {4} -6z ^ {2} +1}} \, dz.}

Os pólos desta função estão em $1 \pm \sqrt 2$ e $-1 \pm \sqrt 2$ . Destes, $1 + \sqrt 2$ e $-1 - \sqrt 2$ estão fora do círculo unitário (mostrado em vermelho, não na escala), enquanto $1 - \sqrt 2$ e $-1 + \sqrt 2$ estão dentro do círculo unitário (mostrado em azul). Os resíduos correspondentes são ambos iguais a $- eu \sqrt 2 / 16$ , de modo que o valor da integral seja

{\ displaystyle I = 2 \ pi i \; 2 \ left (- {\ frac {\ sqrt {2}} {16}} i \ right) = \ pi {\ frac {\ sqrt {2}} {4} }.}

Exemplo 4 - cortes de galhos

Considere a integral real

{\ displaystyle \ int _ {0} ^ {\ infty} {\ frac {\ sqrt {x}} {x ^ {2} + 6x + 8}} \, dx.}

Podemos começar formulando a integral complexa

{\ displaystyle \ int _ {C} {\ frac {\ sqrt {z}} {z ^ {2} + 6z + 8}} \, dz = I.}

Podemos usar a fórmula integral de Cauchy ou o teorema do resíduo novamente para obter os resíduos relevantes. No entanto, o importante a notar é que $z 1/2 = e (Log z) / 2$ , portanto $z 1/2$ tem um corte de ramo . Isso afeta a nossa escolha do contorno $C$ . Normalmente, o corte do ramo de logaritmo é definido como o eixo real negativo, no entanto, isso torna o cálculo da integral um pouco mais complicado, portanto, o definimos como o eixo real positivo.

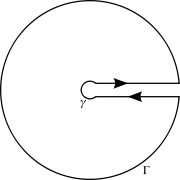
Em seguida, usamos o chamado contorno de buraco de fechadura , que consiste em um pequeno círculo sobre a origem do raio $ε$ , digamos, estendendo-se até um segmento de reta paralelo e próximo ao eixo real positivo, mas sem tocá-lo, até um círculo quase completo, retornando a um segmento de reta paralelo, próximo e abaixo do eixo real positivo no sentido negativo, retornando ao pequeno círculo no meio.

Observe que $z = -2$ e $z = -4$ estão dentro do grande círculo. Esses são os dois pólos restantes, deriváveis fatorando o denominador do integrando. O ponto de ramificação em $z = 0$ foi evitado por meio de um desvio em torno da origem.

Seja $γ$ o pequeno círculo de raio $ε$ , $Γ$ o maior, com raio $R$ , então

{\ displaystyle \ int _ {C} = \ int _ {\ varepsilon} ^ {R} + \ int _ {\ Gamma} + \ int _ {R} ^ {\ varejpsilon} + \ int _ {\ gamma}. }

Pode-se mostrar que as integrais sobre $Γ$ e $γ$ tendem a zero quando $ε \to 0$ e $R \to \infty$ , por um argumento de estimação acima, que deixa dois termos. Agora, como $z 1/2 = e (Log z) / 2$ , no contorno fora do corte do ramo, ganhamos 2 $π$ no argumento ao longo de $γ$ . (Pela identidade de Euler , $e i π$ representa o vetor unitário, que, portanto, tem $π$ como seu log. Este $π$ é o que se entende pelo argumento de $z$ . O coeficiente de1/2nos força a usar 2 $π$ .) Então

{\ displaystyle {\ begin {alinhado} \ int _ {R} ^ {\ varepsilon} {\ frac {\ sqrt {z}} {z ^ {2} + 6z + 8}} \, dz & = \ int _ { R} ^ {\ varepsilon} {\ frac {e ^ {{\ frac {1} {2}} \ operatorname {Log} z}} {z ^ {2} + 6z + 8}} \, dz \\ [ 6pt] & = \ int _ {R} ^ {\ varepsilon} {\ frac {e ^ {{\ frac {1} {2}} (\ log | z | + i \ arg {z})}} {z ^ {2} + 6z + 8}} \, dz \\ [6pt] & = \ int _ {R} ^ {\ varepsilon} {\ frac {e ^ {{\ frac {1} {2}} \ log | z |} e ^ {{\ frac {1} {2}} (2 \ pi i)}} {z ^ {2} + 6z + 8}} \, dz \\ [6pt] & = \ int _ {R} ^ {\ varepsilon} {\ frac {e ^ {{\ frac {1} {2}} \ log | z |} e ^ {\ pi i}} {z ^ {2} + 6z + 8} } \, dz \\ [6pt] & = \ int _ {R} ^ {\ varepsilon} {\ frac {- {\ sqrt {z}}} {z ^ {2} + 6z + 8}} \, dz \\ [6pt] & = \ int _ {\ varejpsilon} ^ {R} {\ frac {\ sqrt {z}} {z ^ {2} + 6z + 8}} \, dz. \ End {alinhado}} }

Portanto:

{\ displaystyle \ int _ {C} {\ frac {\ sqrt {z}} {z ^ {2} + 6z + 8}} \, dz = 2 \ int _ {0} ^ {\ infty} {\ frac {\ sqrt {x}} {x ^ {2} + 6x + 8}} \, dx.}

Usando o teorema do resíduo ou a fórmula integral de Cauchy (primeiro empregando o método das frações parciais para derivar a soma de duas integrais de contorno simples), obtém-se

{\ displaystyle \ pi i \ left ({\ frac {i} {\ sqrt {2}}} - i \ right) = \ int _ {0} ^ {\ infty} {\ frac {\ sqrt {x}} {x ^ {2} + 6x + 8}} \, dx = \ pi \ left (1 - {\ frac {1} {\ sqrt {2}}} \ right). \ quad \ square}

Exemplo 5 - o quadrado do logaritmo

Esta seção trata de um tipo de integral do qual

{\ displaystyle \ int _ {0} ^ {\ infty} {\ frac {\ log x} {\ left (1 + x ^ {2} \ right) ^ {2}}} \, dx}

é um exemplo.

Para calcular essa integral, usa-se a função

{\ displaystyle f (z) = \ left ({\ frac {\ log z} {1 + z ^ {2}}} \ right) ^ {2}}

e o ramo do logaritmo correspondente a

-π <arg z \leq π

.

Vamos calcular a integral de $f (z)$ ao longo do contorno do buraco da fechadura mostrado à direita. Como se constatou que esta integral é um múltiplo da integral inicial que desejamos calcular e pelo teorema do resíduo de Cauchy, temos

{\ displaystyle {\ begin {alinhado} \ left (\ int _ {R} + \ int _ {M} + \ int _ {N} + \ int _ {r} \ right) f (z) \, dz & = 2 \ pi i {\ big (} \ operatorname {Res} _ {z = i} f (z) + \ operatorname {Res} _ {z = -i} f (z) {\ big)} \\ & = 2 \ pi i \ left (- {\ frac {\ pi} {4}} + {\ frac {1} {16}} i \ pi ^ {2} - {\ frac {\ pi} {4}} - {\ frac {1} {16}} i \ pi ^ {2} \ right) \\ & = - i \ pi ^ {2}. \ end {alinhado}}}

Seja $R$ o raio do círculo grande $er$ o raio do círculo pequeno. Iremos designar a linha superior por $M$ , e a linha inferior por $N$ . Como antes, tomamos o limite quando $R \to \infty$ e $r \to 0$ . As contribuições dos dois círculos desaparecem. Por exemplo, um tem o seguinte limite superior com o lema $ML$ :

{\ displaystyle \ left | \ int _ {R} f (z) \, dz \ right | \ leq 2 \ pi R {\ frac {(\ log R) ^ {2} + \ pi ^ {2}} { \ left (R ^ {2} -1 \ right) ^ {2}}} \ a 0.}

A fim de calcular as contribuições de $M$ e $N$ , definimos $z = - x + iε$ em $M$ e $z = - x - iε$ em $N$ , com $0 < x <\infty$ :

{\ displaystyle {\ begin {alinhados} -i \ pi ^ {2} & = \ left (\ int _ {R} + \ int _ {M} + \ int _ {N} + \ int _ {r} \ direita) f (z) \, dz \\ [6pt] & = \ left (\ int _ {M} + \ int _ {N} \ right) f (z) \, dz && \ int _ {R}, \ int _ {r} {\ mbox {vanish}} \\ [6pt] & = - \ int _ {\ infty} ^ {0} \ left ({\ frac {\ log (-x + i \ varepsilon)} { 1 + (- x + i \ varepsilon) ^ {2}}} \ right) ^ {2} \, dx- \ int _ {0} ^ {\ infty} \ left ({\ frac {\ log (-xi \ varepsilon)} {1 + (- xi \ varepsilon) ^ {2}}} \ right) ^ {2} \, dx \\ [6pt] & = \ int _ {0} ^ {\ infty} \ left ( {\ frac {\ log (-x + i \ varepsilon)} {1 + (- x + i \ varejpsilon) ^ {2}}} \ right) ^ {2} \, dx- \ int _ {0} ^ {\ infty} \ left ({\ frac {\ log (-xi \ varepsilon)} {1 + (- xi \ varepsilon) ^ {2}}} \ right) ^ {2} \, dx \\ [6pt] & = \ int _ {0} ^ {\ infty} \ left ({\ frac {\ log x + i \ pi} {1 + x ^ {2}}} \ right) ^ {2} \, dx- \ int _ {0} ^ {\ infty} \ left ({\ frac {\ log xi \ pi} {1 + x ^ {2}}} \ right) ^ {2} \, dx && \ varepsilon \ to 0 \\ & = \ int _ {0} ^ {\ infty} {\ frac {(\ log x + i \ pi) ^ {2} - (\ log xi \ pi) ^ {2}} {\ left (1 + x ^ {2} \ right) ^ {2}}} \, dx \\ [6pt] & = \ int _ {0} ^ {\ infty} {\ frac {4 \ pi i \ log x} {\ left ( 1 + x ^ {2} \ right) ^ {2}}} \, dx \\ [6pt] & = 4 \ pi i \ int _ {0} ^ {\ infty} {\ frac {\ log x} { \ le ft (1 + x ^ {2} \ right) ^ {2}}} \, dx \ end {alinhados}}}

que dá

{\ displaystyle \ int _ {0} ^ {\ infty} {\ frac {\ log x} {\ left (1 + x ^ {2} \ right) ^ {2}}} \, dx = - {\ frac {\ pi} {4}}.}

Exemplo 6 - logaritmos e o resíduo no infinito

Procuramos avaliar

{\ displaystyle I = \ int _ {0} ^ {3} {\ frac {x ^ {\ frac {3} {4}} (3-x) ^ {\ frac {1} {4}}} {5 -x}} \, dx.}

Isso requer um estudo cuidadoso de

{\ displaystyle f (z) = z ^ {\ frac {3} {4}} (3-z) ^ {\ frac {1} {4}}.}

Construiremos $f (z) de$ forma que tenha um corte de ramo em $[0, 3]$ , mostrado em vermelho no diagrama. Para fazer isso, escolhemos dois ramos do logaritmo, definindo

{\ displaystyle z ^ {\ frac {3} {4}} = \ exp \ left ({\ frac {3} {4}} \ log z \ right) \ quad {\ mbox {where}} - \ pi \ leq \ arg z <\ pi}

e

{\ displaystyle (3-z) ^ {\ frac {1} {4}} = \ exp \ left ({\ frac {1} {4}} \ log (3-z) \ right) \ quad {\ mbox {onde}} 0 \ leq \ arg (3-z) <2 \ pi.}

O corte de $z .mw-parser-output .frac{white-space:nowrap}.mw-parser-output .frac .num,.mw-parser-output .frac .den{font-size:80%;line-height:0;vertical-align:super}.mw-parser-output .frac .den{vertical-align:sub}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px} 3 ⁄ 4$ é, portanto, $(-\infty, 0]$ e o corte de $(3 - z) 1/4$ é $(-\infty, 3]$ . É fácil ver que o corte do produto dos dois, ou seja, $f (z)$ , é $[0, 3]$ , porque $f (z)$ é realmente contínuo em $(-\infty, 0)$ . Isso ocorre porque quando $z = - r <0$ e nos aproximamos do corte de cima, $f (z)$ tem o valor

{\ displaystyle r ^ {\ frac {3} {4}} e ^ {{\ frac {3} {4}} \ pi i} (3 + r) ^ {\ frac {1} {4}} e ^ {{\ frac {2} {4}} \ pi i} = r ^ {\ frac {3} {4}} (3 + r) ^ {\ frac {1} {4}} e ^ {{\ frac {5} {4}} \ pi i}.}

Quando nos aproximamos de baixo, $f (z)$ tem o valor

{\ displaystyle r ^ {\ frac {3} {4}} e ^ {- {\ frac {3} {4}} \ pi i} (3 + r) ^ {\ frac {1} {4}} e ^ {{\ frac {0} {4}} \ pi i} = r ^ {\ frac {3} {4}} (3 + r) ^ {\ frac {1} {4}} e ^ {- { \ frac {3} {4}} \ pi i}.}

Mas

{\ displaystyle e ^ {- {\ frac {3} {4}} \ pi i} = e ^ {{\ frac {5} {4}} \ pi i},}

para que tenhamos continuidade em todo o corte. Isso é ilustrado no diagrama, onde os dois círculos pretos orientados são rotulados com o valor correspondente do argumento do logaritmo usado em $z 3 ⁄ 4$ e $(3 - z) 1/4$ .

Usaremos o contorno mostrado em verde no diagrama. Para fazer isso, devemos calcular o valor de $f (z)$ ao longo dos segmentos de linha logo acima e logo abaixo do corte.

Seja $z = r$ (no limite, ou seja, conforme os dois círculos verdes diminuem para o raio zero), onde $0 \leq r \leq 3$ . Ao longo do segmento superior, descobrimos que $f (z)$ tem o valor

{\ displaystyle r ^ {\ frac {3} {4}} e ^ {{\ frac {0} {4}} \ pi i} (3-r) ^ {\ frac {1} {4}} e ^ {{\ frac {2} {4}} \ pi i} = ir ^ {\ frac {3} {4}} (3-r) ^ {\ frac {1} {4}}}

e ao longo do segmento inferior,

{\ displaystyle r ^ {\ frac {3} {4}} e ^ {{\ frac {0} {4}} \ pi i} (3-r) ^ {\ frac {1} {4}} e ^ {{\ frac {0} {4}} \ pi i} = r ^ {\ frac {3} {4}} (3-r) ^ {\ frac {1} {4}}.}

Conclui-se que a integral de $f (z) / 5 - z$ ao longo do segmento superior é $- iI$ no limite, e ao longo do segmento inferior, $eu$ .

Se pudermos mostrar que as integrais ao longo dos dois círculos verdes desaparecem no limite, então também temos o valor de $I$ , pelo teorema do resíduo de Cauchy . Seja o raio dos círculos verdes $ρ$ , onde $ρ <0,001$ e $ρ \to 0$ , e aplique a desigualdade $ML$ . Para o círculo $C L$ à esquerda, encontramos

{\ displaystyle \ left | \ int _ {C _ {\ mathrm {L}}} {\ frac {f (z)} {5-z}} dz \ right | \ leq 2 \ pi \ rho {\ frac {\ rho ^ {\ frac {3} {4}} 3.001 ^ {\ frac {1} {4}}} {4.999}} \ in {\ mathcal {O}} \ left (\ rho ^ {\ frac {7} {4}} \ right) \ to 0.}

Da mesma forma, para o círculo $C R$ à direita, temos

{\ displaystyle \ left | \ int _ {C _ {\ mathrm {R}}} {\ frac {f (z)} {5-z}} dz \ right | \ leq 2 \ pi \ rho {\ frac {3.001 ^ {\ frac {3} {4}} \ rho ^ {\ frac {1} {4}}} {1.999}} \ in {\ mathcal {O}} \ left (\ rho ^ {\ frac {5} {4}} \ right) \ to 0.}

Agora, usando o teorema do resíduo de Cauchy , temos

{\ displaystyle (-i + 1) I = -2 \ pi i \ left (\ operatorname {Res} _ {z = 5} {\ frac {f (z)} {5-z}} + \ operatorname {Res } _ {z = \ infty} {\ frac {f (z)} {5-z}} \ right).}

onde o sinal de menos é devido ao sentido horário em torno dos resíduos. Usando a ramificação do logaritmo anterior, claramente

{\ displaystyle \ operatorname {Res} _ {z = 5} {\ frac {f (z)} {5-z}} = - 5 ^ {\ frac {3} {4}} e ^ {{\ frac { 1} {4}} \ log (-2)}.}

O pólo é mostrado em azul no diagrama. O valor simplifica para

{\ displaystyle -5 ^ {\ frac {3} {4}} e ^ {{\ frac {1} {4}} (\ log 2+ \ pi i)} = - e ^ {{\ frac {1} {4}} \ pi i} 5 ^ {\ frac {3} {4}} 2 ^ {\ frac {1} {4}}.}

Usamos a seguinte fórmula para o resíduo no infinito:

{\ displaystyle \ operatorname {Res} _ {z = \ infty} h (z) = \ operatorname {Res} _ {z = 0} \ left (- {\ frac {1} {z ^ {2}}} h \ left ({\ frac {1} {z}} \ right) \ right).}

Substituindo, encontramos

{\ displaystyle {\ frac {1} {5 - {\ frac {1} {z}}}} = - z \ left (1 + 5z + 5 ^ {2} z ^ {2} + 5 ^ {3} z ^ {3} + \ cdots \ right)}

e

{\ displaystyle \ left ({\ frac {1} {z ^ {3}}} \ left (3 - {\ frac {1} {z}} \ right) \ right) ^ {\ frac {1} {4 }} = {\ frac {1} {z}} (3z-1) ^ {\ frac {1} {4}} = {\ frac {1} {z}} e ^ {{\ frac {1} { 4}} \ pi i} (1-3z) ^ {\ frac {1} {4}},}

onde usamos o fato de que

-1 = e π i

para o segundo ramo do logaritmo. Em seguida, aplicamos a expansão binomial, obtendo

{\ displaystyle {\ frac {1} {z}} e ^ {{\ frac {1} {4}} \ pi i} \ left (1- {1/4 \ escolha 1} 3z + {1/4 \ escolha 2} 3 ^ {2} z ^ {2} - {1/4 \ escolha 3} 3 ^ {3} z ^ {3} + \ cdots \ right).}

A conclusão é que

{\ displaystyle \ operatorname {Res} _ {z = \ infty} {\ frac {f (z)} {5-z}} = e ^ {{\ frac {1} {4}} \ pi i} \ left (5 - {\ frac {3} {4}} \ right) = e ^ {{\ frac {1} {4}} \ pi i} {\ frac {17} {4}}.}

Finalmente, segue-se que o valor de $I$ é

{\ displaystyle I = 2 \ pi i {\ frac {e ^ {{\ frac {1} {4}} \ pi i}} {- 1 + i}} \ left ({\ frac {17} {4} } -5 ^ {\ frac {3} {4}} 2 ^ {\ frac {1} {4}} \ right) = 2 \ pi 2 ^ {- {\ frac {1} {2}}} \ left ({\ frac {17} {4}} - 5 ^ {\ frac {3} {4}} 2 ^ {\ frac {1} {4}} \ right)}

que produz

{\ displaystyle I = {\ frac {\ pi} {2 {\ sqrt {2}}}} \ left (17-5 ^ {\ frac {3} {4}} 2 ^ {\ frac {9} {4 }} \ right) = {\ frac {\ pi} {2 {\ sqrt {2}}}} \ left (17-40 ^ {\ frac {3} {4}} \ right).}

Avaliação com teorema de resíduo

Usando o teorema do resíduo , podemos avaliar integrais de contorno fechado. A seguir estão exemplos de como avaliar integrais de contorno com o teorema do resíduo.

Usando o teorema do resíduo, vamos avaliar essa integral de contorno.

{\ displaystyle \ oint _ {C} {\ frac {e ^ {z}} {z ^ {3}}} \, dz}

Como uma atualização, o teorema do resíduo afirma

{\ displaystyle \ oint _ {C} f (z) = 2 \ pi i \ cdot \ sum \ operatorname {Res} (f, a_ {k}),}

onde está o resíduo de . ${\ displaystyle \ operatorname {Res}}$ ${\ displaystyle f (z)}$

${\ displaystyle f (z)}$ tem apenas um pólo,. A partir disso, podemos determinar o resíduo de ser ${\ displaystyle f (z)}$ ${\ displaystyle {\ tfrac {1} {2}}}$

{\ displaystyle {\ begin {alinhado} \ oint _ {C} f (z) & = \ oint _ {C} {\ frac {e ^ {z}} {z ^ {3}}} \\ & = 2 \ pi i \ cdot \ operatorname {Res} _ {z = 0} f (z) \\ & = 2 \ pi i \ operatorname {Res} _ {z = 0} {\ frac {e ^ {z}} { z ^ {3}}} \\ & = 2 \ pi i \ cdot {\ frac {1} {2}} \\ & = \ pi i \ end {alinhado}}}

Assim, usando o teorema do resíduo , podemos determinar:

{\ displaystyle \ oint _ {C} {\ frac {e ^ {z}} {z ^ {3}}} = \ pi i.}

Integrais de contorno multivariáveis

Para resolver integrais de contorno multivariáveis (ou seja , integrais de superfície , integrais de volume complexas e integrais de ordem superior ), devemos usar o teorema da divergência . Por agora, vamos ser intercambiáveis com . Ambos servirão como divergência do campo vetorial denotado como . Este teorema afirma: ${\ displaystyle \ nabla}$ ${\ displaystyle \ operatorname {Div}}$ ${\ displaystyle \ mathbf {F}}$

{\ displaystyle \ underbrace {\ int \ cdots \ int _ {U}} _ {n} \ operatorname {div} (\ mathbf {F}) \, dV = \ underbrace {\ oint \ cdots \ oint _ {\ partial U}} _ {n-1} \ mathbf {F} \ cdot \ mathbf {n} \, dS}

Além disso, também precisamos avaliar onde está uma notação alternativa de . A divergência de qualquer dimensão pode ser descrita como ${\ displaystyle \ nabla \ cdot \ mathbf {F}}$ ${\ displaystyle \ nabla \ cdot \ mathbf {F}}$ ${\ displaystyle \ operatorname {div} (\ mathbf {F})}$

{\ displaystyle {\ begin {alinhado} \ operatorname {div} (\ mathbf {F}) & = \ nabla \ cdot \ mathbf {F} \\ & = \ left ({\ frac {\ partial} {\ partial u }}, {\ frac {\ parcial} {\ parcial x}}, {\ frac {\ parcial} {\ parcial y}}, {\ frac {\ parcial} {\ parcial z}}, \ pontos \ direita) \ cdot (F_ {u}, F_ {x}, F_ {y}, F_ {z}, \ dots) \\ & = \ left ({\ frac {\ partial F_ {u}} {\ partial u}} + {\ frac {\ parcial F_ {x}} {\ parcial x}} + {\ frac {\ parcial F_ {y}} {\ parcial y}} + {\ frac {\ parcial F_ {z}} {\ parcial z}} + \ cdots \ direita) \ end {alinhado}}}

Exemplo 1

Deixe o campo vetorial e seja limitado pelo seguinte ${\ displaystyle \ mathbf {F} = \ sin (2x) + \ sin (2y) + \ sin (2z)}$

{\ displaystyle {0 \ leq x \ leq 1} \ quad {0 \ leq y \ leq 3} \ quad {-1 \ leq z \ leq 4}}

A integral de contorno duplo correspondente seria configurada como tal:

$\ oiint$

{\ displaystyle {\ scriptstyle S}}

{\ displaystyle \ mathbf {F} \ cdot \ mathbf {n} \, dS}

Agora avaliamos . Enquanto isso, vamos configurar a integral tripla correspondente: ${\ displaystyle \ nabla \ cdot \ mathbf {F}}$

{\ displaystyle {\ begin {alinhados} & = \ iiint _ {V} \ left ({\ frac {\ partial F_ {x}} {\ partial x}} + {\ frac {\ partial F_ {y}} { \ parcial y}} + {\ frac {\ parcial F_ {z}} {\ parcial z}} \ direita) dV \\ [6pt] & = \ iiint _ {V} \ esquerda ({\ frac {\ parcial \ sin (2x)} {\ parcial x}} + {\ frac {\ parcial \ sin (2y)} {\ parcial y}} + {\ frac {\ parcial \ sin (2z)} {\ parcial z}} \ direita) dV \\ [6pt] & = \ iiint _ {V} 2 \ left (\ cos (2x) + \ cos (2y) + \ cos (2z) \ right) dV \\ [6pt] & = \ int _ {0} ^ {1} \ int _ {0} ^ {3} \ int _ {- 1} ^ {4} 2 (\ cos (2x) + \ cos (2y) + \ cos (2z)) \ , dx \, dy \, dz \\ [6pt] & = \ int _ {0} ^ {1} \ int _ {0} ^ {3} (10 \ cos (2y) + \ sin (8) + \ sin (2) +10 \ cos (z)) \, dy \, dz \\ [6pt] & = \ int _ {0} ^ {1} (30 \ cos (2z) +3 \ sin (2) + 3 \ sin (8) +5 \ sin (6)) \, dz \\ [6pt] & = 18 \ sin (2) +3 \ sin (8) +5 \ sin (6) \ end {alinhado}} }

Exemplo 2

Deixe o campo vetorial e observe que existem 4 parâmetros neste caso. Deixe este campo vetorial ser limitado pelo seguinte: ${\ displaystyle \ mathbf {F} = u ^ {4} + x ^ {5} + y ^ {6} + z ^ {- 3}}$

{\ displaystyle {0 \ leq x \ leq 1} \ quad {-10 \ leq y \ leq 2 \ pi} \ quad {4 \ leq z \ leq 5} \ quad {-1 \ leq u \ leq 3}}

Para avaliar isso, devemos utilizar o teorema da divergência como afirmado antes, e devemos avaliar . Deixar ${\ displaystyle \ nabla \ cdot \ mathbf {F}}$ ${\ displaystyle dV = dx \, dy \, dz \, du}$

$\ oiiint$

{\ displaystyle {\ scriptstyle S}}

{\ displaystyle \ mathbf {F} \ cdot \ mathbf {n} \, dS}

{\ displaystyle {\ begin {alinhados} & = \ iiiint _ {V} \ left ({\ frac {\ partial F_ {u}} {\ partial u}} + {\ frac {\ partial F_ {x}} { \ parcial x}} + {\ frac {\ parcial F_ {y}} {\ parcial y}} + {\ frac {\ parcial F_ {z}} {\ parcial z}} \ direita) \, dV \\ [ 6pt] & = \ iiiint _ {V} \ left ({\ frac {\ parcial u ^ {4}} {\ parcial u}} + {\ frac {\ parcial x ^ {5}} {\ parcial x}} + {\ frac {\ parcial y ^ {6}} {\ parcial y}} + {\ frac {\ parcial z ^ {- 3}} {\ parcial z}} \ direita) \, dV \\ [6pt] & = \ iiiint _ {V} {\ frac {4u ^ {3} z ^ {4} + 5x ^ {4} z ^ {4} + 5y ^ {4} z ^ {4} -3} {z ^ {4}}} \, dV \\ [6pt] & = \ iiiint _ {V} {\ frac {4u ^ {3} z ^ {4} + 5x ^ {4} z ^ {4} + 5y ^ { 4} z ^ {4} -3} {z ^ {4}}} \, dV \\ [6pt] & = \ int _ {0} ^ {1} \ int _ {- 10} ^ {2 \ pi } \ int _ {4} ^ {5} \ int _ {- 1} ^ {3} {\ frac {4u ^ {3} z ^ {4} + 5x ^ {4} z ^ {4} + 5y ^ {4} z ^ {4} -3} {z ^ {4}}} \, dV \\ [6pt] & = \ int _ {0} ^ {1} \ int _ {- 10} ^ {2 \ pi} \ int _ {4} ^ {5} \ left ({\ frac {4 (3u ^ {4} z ^ {3} + 3y ^ {6} + 91z ^ {3} +3)} {3z ^ {3}}} \ right) \, dy \, dz \, du \\ [6pt] & = \ int _ {0} ^ {1} \ int _ {- 10} ^ {2 \ pi} \ left ( 4u ^ {4} + {\ frac {743440} {21}} + {\ frac {4} {z ^ {3}}} \ right) \, dz \, du \\ [6pt] & = \ int _ {0} ^ {1} \ left (- {\ frac {1} {2 \ pi ^ {2}}} + {\ frac {1486880 \ pi} {21}} + 8 \ pi u ^ {4} + 40u ^ {4} + {\ frac {371720021} {1050}} \ right) \, du \\ [6pt] & = {\ frac {371728421} {1050}} + {\ frac {14869136 \ pi ^ {3} -105} {210 \ pi ^ {2}}} \\ [6pt] & \ approx {576468,77} \ end {alinhado}}}

Assim, podemos avaliar uma integral de contorno com . Podemos usar o mesmo método para avaliar integrais de contorno para qualquer campo vetorial com bem. ${\ displaystyle n = 4}$ ${\ displaystyle n> 4}$

Representação integral

Uma representação integral de uma função é uma expressão da função envolvendo uma integral de contorno. Várias representações integrais são conhecidas por muitas funções especiais . As representações integrais podem ser importantes por razões teóricas, por exemplo, dando continuação analítica ou equações funcionais , ou às vezes para avaliações numéricas .

Contorno de Hankel

Por exemplo, a definição original da função zeta de Riemann $ζ (s)$ por meio de uma série de Dirichlet ,

{\ displaystyle \ zeta (s) = \ sum _ {n = 1} ^ {\ infty} {\ frac {1} {n ^ {s}}},}

é válido apenas para $Re (s)> 1$ . Mas

{\ displaystyle \ zeta (s) = - {\ frac {\ Gamma (1-s)} {2 \ pi i}} \ int _ {H} {\ frac {(-t) ^ {s-1}} {e ^ {t} -1}} dt,}

onde a integração é feita sobre o contorno de Hankel $H$ , é válido para todos os complexos s diferentes de 1.

Veja também

Referências

Leitura adicional

Titchmarsh, EC (1939), The Theory of Functions (2ª ed.), Oxford University Press, ISBN 0-19-853349-7
Jean Jacquelin, Marko Riedel, Branche univalente , Les-Mathematiques.net , em francês.
Marko Riedel et al., Problème d'intégrale , Les-Mathematiques.net , em francês.
Marko Riedel et al., Integral por resíduo , math.stackexchange.com .
WWL Chen, introdução à análise complexa
Vários autores, sin límites ni cotas , es.ciencia.matematicas , em espanhol.

links externos

"Complex integration, method of" , Encyclopedia of Mathematics , EMS Press , 2001 [1994]

Languages

In other projects

Integração de contorno - Contour integration

Conteúdo

Curvas no plano complexo

Curvas suaves direcionadas

Contornos

Integrais de contorno

Para funções contínuas

Como uma generalização da integral de Riemann

Métodos diretos

Exemplo

Aplicações de teoremas integrais

Exemplo 1

Usando a fórmula integral de Cauchy

Usando o método de resíduos

Nota de contorno

Exemplo 2 - distribuição de Cauchy

Exemplo 3 - integrais trigonométricas

Exemplo 3a - integrais trigonométricas, o procedimento geral

Exemplo 4 - cortes de galhos

Exemplo 5 - o quadrado do logaritmo

Exemplo 6 - logaritmos e o resíduo no infinito

Avaliação com teorema de resíduo

Integrais de contorno multivariáveis

Exemplo 1

Exemplo 2

Representação integral

Veja também

Referências

Leitura adicional

links externos